基于改进SW滑楔模型刚性抗滑桩极限滑坡推力智能优化计算方法
陈昌富,戴宇佳,梁冠亭,朱剑锋
(1.湖南大学岩土工程研究所,湖南长沙 410082;2.宁波大学建筑工程与环境学院,浙江宁波 315211)
工程中遇到的滑坡大多都是沿着一个或多个软弱层面而产生滑动(图1)。对于此类滑坡,如果滑动面相对较浅,通常是采用刚性抗滑桩加固。一般刚性桩的位移量较小,如果滑体在桩位处的剩余下滑力大于桩后土体所能提供的最大被动土压力,则随着滑体沿软弱层面不断滑移,桩后土体会逐渐形成一个三维被动滑动土楔(图1),此时,作用于桩上的极限滑坡推力就变为由被动三维滑动土楔所产生的推力(即被动土压力)。因此,对于沿一软弱层面的滑坡,在滑体处于极限平衡状态下,作用于刚性抗滑桩上的极限滑坡推力,应是由滑体所产生的剩余下滑力和由桩后三维滑动土楔所产生的被动土压力两者中较小者。剩余下滑力的计算目前已比较成熟,并已形成规范[1~2],而对于桩后三维滑动土楔所产生的被动土压力的计算问题,目前尚未完善,因此本文尝试借用最近国内外关注较多的应变楔(SW)模型[3]来解决。

图1 边坡分析简图Fig.1 Diagram for the slope analysis
应变楔(SW)模型最早由Norris等[3]提出,并用其分析了桩顶受水平集中荷载作用桩,得到了在三维土楔体作用下桩身受力分布;李彬[4]考虑了应力集中现象,假定作用在楔形体面上的应力变化Δσh在水平切面上呈三角形分布,并运用于群桩受力分析;李忠诚等[5]将应变楔模型应用于被动桩,建立了被动拱-主动楔模型,实现了三维桩土相互作用计算;Youngho Kim等[6]采用三维非线性有限元分析,验证了楔体模型的合理性,并进行了多组水平受荷桩试验,并在应变楔模型基础上考虑楔体两侧的土体受力,得到了桩上受力沿桩长呈双曲线分布;Ashour等[7]将应变楔模型与弹性地基梁法结合,运用到边坡稳定分析中,通过迭代求出弹性桩上的推力分布。
现有SW模型中,均假定滑动楔体底部滑面为平面,这与实际情况往往不符。并且,由于边坡坡角越大,最大侧向变形越大[8],SW模型未考虑斜坡的影响,计算结果不够准确。为此,本文结合传递系数法,以SW模型为基础,假定滑楔底面为对数螺旋线面,得到改进SW滑楔模型。同时,基于倾斜薄层单元法,引入智能优化算法——粒子群优化(PSO)算法,计算极限滑坡推力Pult。结合算例分别探讨桩位、桩径以及土体参数的变异系数对极限滑坡推力Pult的影响。
1 受力分析模型
基于SW模型,为便于分析,改进SW滑楔模型作了如下假定:
(1)刚性桩加固的滑坡,桩身不发生位移,边坡滑体沿软弱层面产生足够的滑移,使桩后土体达到被动极限平衡状态,形成被动滑楔体(图1)。
(2)被动滑楔体以yOz面对称(图2),其两侧滑面为从桩背沿y轴向外扩展的平面,底部破裂面为绕x轴转动的对数螺线曲面(图3)。

图2 计算模型示意图Fig.2 Schematic diagram of the calculating model

图3 对数螺旋线滑动面Fig.3 Slip surface composed of the log-spiral surface
(3)将被动滑楔体斜分为薄层单元,单元间沿x轴方向切向层间力因对称相互抵消,只考虑竖向作用的层间力。
(4)作用于桩上的推力Pi沿深度呈线性分布。
1.1 破裂面参数的确定
如图3所示,以桩顶处O点为坐标原点,建立直角坐标系,将土体分成n个薄层单元。
对数螺旋线滑动面方程为:

式中:ri——第i个薄层滑面对数螺线的半径;
r0——滑面对数螺线的初始半径;
a——系数,可取 a=tan2(45°-2φ/3)[9];
φ——土的内摩擦角;
θi——第i个薄层单元的旋转角度。
设对数螺线在第i个薄层的斜率为ki,滑动面近似为直线[10],对应的滑动面倾角为 αi,初始半径 r0与水平面的夹角为ζ,则:

1.2 桩上滑坡推力计算
桩上滑坡推力计算模型如图2。取其中第i个薄层单元进行受力分析(图4)。斜薄层单元在其斜平面上呈梯形状,其上底宽等于桩的宽度,下底宽设为li。若设斜薄层单元水平投影长度为bi,则根据几何关系可知:

图4 薄层单元受力分析Fig.4 Thin-layer element analysis

式中:D——桩径(m);
φm——土的伞角。
由于底部第n个薄层单元在纵剖面上近似为三角形,于是有:

薄层单元沿y轴、z轴方向上力的平衡方程为:
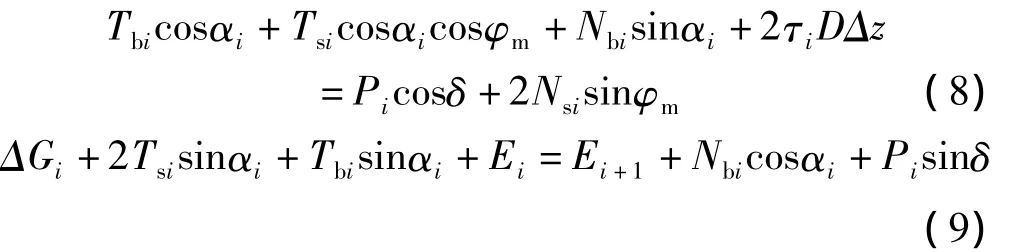
式中:Pi——桩上滑坡推力,与水平面夹角为δ;
Ei,Ei+1——竖向作用的层间力;
Nsi,Tsi——滑楔侧面法向力与切向力;
Nbi,Tbi——滑楔底面法向力与侧向力。Nbi表现为拉力,取为0。
滑动面上土体处于极限平衡状态,切向力与法向力服从Mohr-Coulomb定律:

式中:ci,φi——滑动面上土体抗剪强度指标;
Asi,Abi——滑楔侧面和底面的表面积。
联立式(8)~(11),可得:

假定桩侧剪应力强度完全发挥,τi=(τult)i,综合考虑粘性土中应变软化、应力历史及不排水强度比对桩侧抗剪强度的影响,根据文献[11]知:

由于破裂面为任意假定对数螺旋线面,取不同的破裂面可求得不同的滑坡推力合力P值,可通过优化方法求出最大滑坡推力Pmax,即为极限滑坡推力Pult,对应的破裂面即为最危险破裂面。
2 PSO搜索破裂面
基于本文提出的改进SW滑楔模型,桩上极限滑坡推力Pult计算可归结为如下优化模型:

本文采用具有良好全局搜索能力的粒子群算法[12](PSO)搜索破裂面。PSO模拟鸟群的捕食行为,每个优化问题的解都是搜索空间中的一个“粒子”。PSO初始化为一群粒子(随机解),通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个最优解来更新自己,一是粒子本身所找到的最优解,另一个是整个种群目前所找到的最优解。

根据以上模型和原理,滑坡推力混合粒子群算法计算步骤如下:
(1)设定粒子群数目,初始化每个粒子的位置矢量 Xi=[xi,1,xi,2]和速度矢量 Vi=[vi,1,vi,2];
(2)根据每个粒子当前的Xi计算其适应度。若gi(X)>0成立,则fitness(i)=f(Xi);否则,将一个远大于极限滑坡推力的值赋给适应度函数作为该粒子的适应值以使其受到惩罚,例如fitness(i)=10000;
(3)对每个微粒,将它的适应值与其经历过的最好位置pbest的适应值作比较,如果较好,则更新pbest,将它的适应值和全局所经历最好位置gbest的适应值作比较,如果较好,则更新gbest;
(4)根据式(18)和(19)更新各粒子的速度和位置,取每个微粒的最好适应值对应的位置作为当前的最好位置,更新gbest;
(5)设定最大迭代次数,达到最大迭代次数后则输出结果,即滑坡推力最大时的ζ、θn值以及极限滑坡推力Pult大小。
3 算例与参数分析
采用文献[7]中给出的两个分析算例(图5),边坡的水平投影距离为L,抗滑桩间距S=3m,桩位至坡脚水平投影距离为Lx。边坡岩土体参数指标如图5,其中滑面抗剪强度参数与土体的相同。

图5 边坡示意图(引自文献[5])Fig.5 Schematic diagram of slope(cited in[5])
3.1 桩位的影响
取桩径D=1.2m,分别采用传递系数法、SW法和本文方法计算不同桩位处的极限滑坡推力Pult,计算结果如图6所示。
由图6可知,当滑体处于极限平衡状态时,Pult随桩位(Lx/L)变化呈现中间大两头小的趋势。在桩位靠近坡顶处,由于滑体产生的剩余下滑力相对较小,桩后不能发展出如图1所示穿出滑体的被动三维滑动土楔,此时的Pult就是滑体所产生的剩余滑坡推力(本文采用传递系数法计算),而如果采用SW法计算就会高估作用于桩上的极限滑坡推力(最大误差达76%)。当桩位处在坡的中下部,滑体产生的剩余下滑力相对较大,桩后土体能够发展出如图1所示被动土楔,此时Pult就等于被动土楔所产生的被动土压力,若仍采用传递系数法计算作用于桩上极限滑坡推力,则计算结果偏大,且最大误差处在坡中,相对误差为16%。
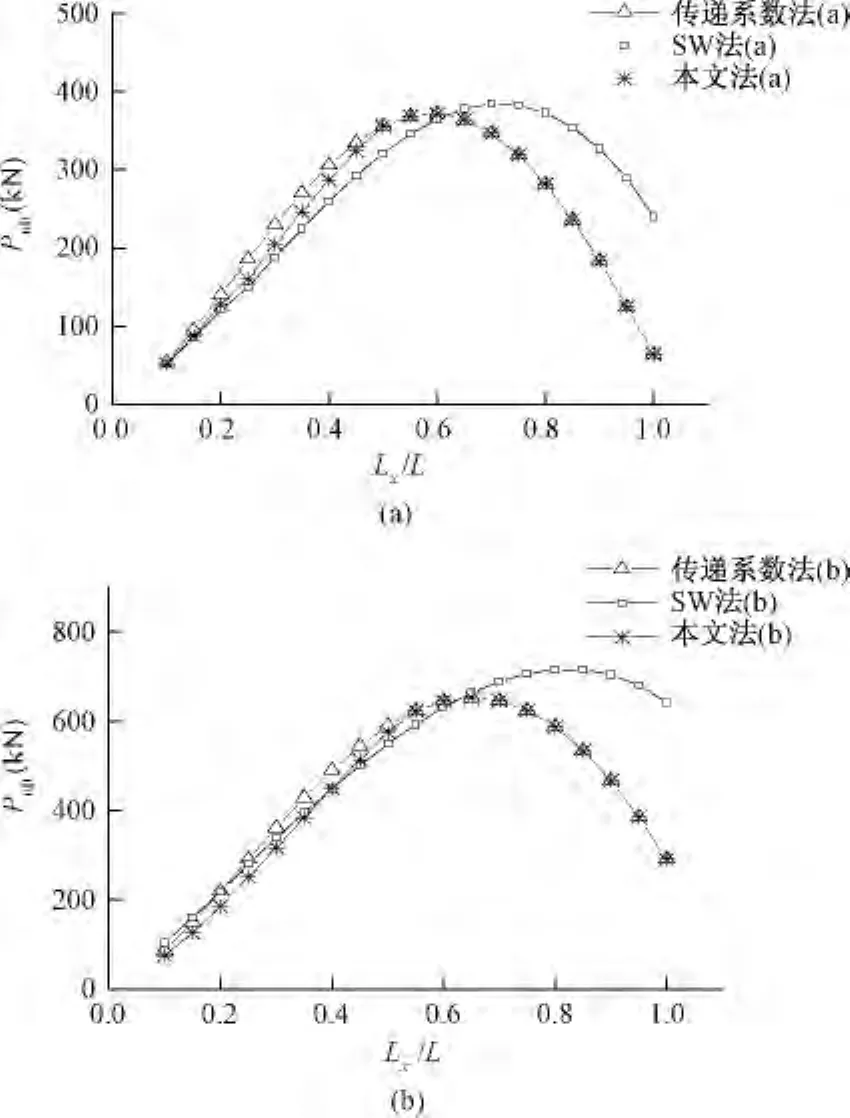
图6 极限滑坡推力Pult随桩位Lx/L的变化Fig.6 Variation in the ultimate landslide thrust Pultwith Lx/L
图6进一步说明,当桩间距较大,桩位设置在坡的中部时,作用于桩上的实际极限滑坡推力小于按规范[13]推荐的传递系数法所得计算结果,因此,根据规范法计算的滑坡推力来设计抗滑桩,偏于保守。而且,已有研究结果表明[14]:与有限元数值法和Morgenstern-Price法相比,采用规范的传递系数法计算滑坡推力,所设计的抗滑桩也偏于保守。
3.2 桩径D的影响
将桩设置于Lx/L=0.5处,桩径D从0.9 m逐渐增大至1.6 m,计算水平极限推力Pult,结果如图7所示。

图7 极限滑坡推力Pult随桩径的变化Fig.7 Variation in the ultimate landslide thrust Pult with pile diameter
由图7可知,Pult与桩径D呈线性关系,随D的增大而增大。与SW法相比,Pult随桩径变化的分布一致,桩径增大对Pult影响较小,Pult增长幅度小于SW法计算结果的增长幅度。
4 土体参数变异性对Pult的影响
以图5边坡(a)为例,将桩设置于Lx/L=0.5处,土体的重度γ1,粘聚力c1,以及内摩擦角φ1的变异系数分别为 δγ1,δc1,δφ1,分析上述 3 个参数的变异性对极限滑坡推力Pult的变异系数δPult的影响。
假定各参数服从正态分布,选取土体参数不同的变异系数分别计算Pult的变异系数δPult(图8)。

图8 不同变异系数对Pult的影响Fig.8 Influences of variable coefficients to Pult
由图8 可知,Pult的变异系数 δPult随土体参数 γ1、c1和 φ1的变异系数 δγ1、δc1和 δφ1的增大而增大。当 δγ1=0.025 ~0.1、δc1=0.1 ~0.4、δφ1=0.1 ~0.25 时,极限滑坡推力Pult的变异系数δPult在0.06~0.2之间变化。由此法得到的极限滑坡推力Pult变异系数δPult,可用于抗滑桩嵌固深度的可靠性分析,从而可简化抗滑桩可靠性设计计算。
5 结论
(1)本文借鉴应变楔(SW)模型,假定破裂面为对数螺旋线面,并引入倾斜薄层单元法,推导了极限滑坡推力计算公式,并利用粒子群优化(PSO)算法搜索计算极限滑坡推力Pult。
(2)算例计算结果表明:当桩间距较大,桩位设置在坡的中部时,作用于桩上的极限滑坡推力Pult小于按规范推荐的传递系数法所得计算结果,而且Pult与桩径基本上呈线性关系。
(3)假定各参数服从正态分布,根据对土体参数不同变异系数进行抽样计算,可得到极限滑坡推力Pult的变异系数 δPult,由此法得到的变异系数 δPult结果可直接用于刚性抗滑桩可靠性分析计算。
(4)考虑土体应力-应变关系,可建立非极限滑坡推力与Pult、土体位移之间的关系式,于是可求得非极限滑坡推力,由于本文篇幅有限,作者将另文阐述。
[1] 中华人民共和国住房和城乡建设部.GB50330-2013建筑边坡工程技术规范[S].北京:中国建筑工业出版社,2014.[Ministry of Housing and Urban-Rural Development of the People's Republic of China.GB50330-2013 Technical code for building slope engineering[S]. Beijing:China Architecture &Building Press,2014.(in Chinese)]
[2] 中华人民共和国住房和城乡建设部.GB50007-2011建筑地基基础设计规范[S].北京:中国建筑工业出版社,2012.[Ministry of Housing and Urban-Rural Development of the People's Republic of China.GB50007- 2011 Code fordesign ofbuilding foundation[S]. Beijing:China Architecture &Building Press,2012.(in Chinese)]
[3] ASHOUR M,NORRIS G,Pilling P.Lateral loading of a pile in layered soil using the strain wedge model[J].Journal of Geotechnical And Geoenvironmental Engineering,ASCE,1998,124(4):303-305.
[4] 李彬.改进SW法及其在桩基水平受荷分析中的应用[D].杭州:浙江大学,2002.[LI B.Analysis Of Laterally Loaded Piles With Modified SW Model[D].Hangzhou:Zhejiang University,2002.(in Chinese)]
[5] 李忠诚,杨敏.被动桩土压力计算的被动拱-主动楔模型[J].岩石力学与工程学报,2006,25(增刊2):4241-4247.[LI Z C,YANG M.Passive ArchingActive Wedge ModelOfSoilPressure Calculation In Passive Piles[J].Rock Mechanics and Engineering,2006,25(Sup2):4241-4247.(in Chinese)]
[6] YOUNGHO Kim,SANGSEOM Jeong,M ASCE,et al.Wedge Failure Analysis of Soil Resistance on Laterally Loaded Piles in Clay[J]. Journalof Geotechnical and Geoenvironmental Engineering,2011,137(7):678-694.
[7] MOHAMED Ashour,HAMED Ardalan.Analysis of pile stabilized slopes based on soil-pile interaction[J].Computers and Geotechnics,2012,39:85-97.
[8] 魏焕卫,孙建平,陈启辉,等.基坑边坡变形的理论计算方法[J].水文地质工程地质,2006,33(2):75-79.[WEI H W,SUN J P,CHEN Q H,et al.Theory Calculation Method of Slope Displacement[J].Hydrogeology& Engineering Geology,2006,33(2):75-79.(in Chinese)]
[9] 赵树德,赵树惠.用对数螺旋线滑动面计算挡土墙主动土压力[J].西安建筑科技大学学报(自然科学版),2002,34(4):343-345.[ZHAO S D,ZHAO S H.Calculation of active earth pressure of retaining wall with logistic spiral sliding surface[J].Journal ofXi’an University ofArchitecture &Technology(Natural Science Edition),2002,34(4):343-345.(in Chinese)]
[10] 陈昌富,曾玉莹,肖淑君,等.基于薄层单元法主动土压力计算的复合遗传算法[J].岩土力学,2006,27(3):398-403.[CHEN C F,ZENG Y Y,XIAO S J,et al.Complex genetic method of active earth pressure based on thin-layer element method[J].Rock and Soil Mechanics,2006,27(3):398-403.(in Chinese)]
[11] API(1993)Recommendedpracticeforplanning,designing and constructing fixed offshore platforms—working stress design[S].API RP2A,20th ed.Washington DC:American Petro-leum Institute.
[12] 龚纯,王正林.精通Matlab最优化计算[M].北京:电子工业出版社,2009.[GONG C,WANG Z L.Proficient in the optimization based on matlab[M].Beijing:Publishing House of Electronics Industry,2009.(in Chinese)]
[13] 交通部第二勘察设计院.公路设计手册(路基)[M].北京:中国铁道出版社,2001.[Second Survey and Design Institute of the Ministry of Communications.Highway Design Manual(Subgrades)[M].Beijing:China Railway Press,2001.(in Chinese)]
[14] 程建军,廖小平,王浩,等.滑坡推力计算方法的对比研究与应用[J].水文地质工程地质,2008,35(1):44-48.[CHENG J J,LIAO X P,WANG H,etal. Comparative research and application of landslide thrust calculation methods [J].Hydrogeology & Engineering Geology,2008,35(1):44-48.(in Chinese)]

