岩溶区地基极限承载力上限有限元数值模拟分析
赵明华,邱志博,张 锐
(湖南大学岩土工程研究所,湖南长沙 410082)
我国疆域辽阔,碳酸盐岩系分布广泛,在水的溶蚀或潜蚀作用下,地层中常发育大小不一的溶洞或土洞,在下文中统称为地下空洞。当基础下方存在地下空洞时,地基实际承载力将受到重要影响,若处理不当可能给工程带来极大的安全隐患和经济损失[1]。为了选取合适的基础形式并制定合理的地基处理方案,需对地下空洞影响下的岩溶区地基承载力问题进行全面分析。为此,本文针对考虑地下空洞影响的岩溶区地基极限承载力确定及影响因素分析开展研究工作,具有重要的工程意义。
目前,对地层中含空洞的岩溶区地基承载力问题进行了大量的研究工作,主要从模型试验、有限元分析和理论研究3个方面展开。在模型试验方面,Kiyosumi M等[2]利用水泥土混合材料模拟坚硬地层,对坚硬地层中存在地下空洞时上部条形基础的承载力进行模型试验与分析,并观察地基破坏机制;刘庭金等[3]对含空洞粘土地基的破坏过程进行室内模型试验和数值模拟研究。有限元分析法是评估地下空洞影响常用的方法,阳军生等[4]、胡 庆 国 等[5]利 用 有 限 元 软 件 (ABAQUS 和ANSYS),分别研究岩溶地区圆形和条形基础下方溶洞顶板的稳定性与承载力问题;彭芳乐等[6]利用PLAXIS分析空洞位置、形状、大小以及地基土的类型等诸因素对浅基础承载力与沉降的影响。在理论研究方面,刘之葵等[7]根据弹性理论,利用莫尔-库仑屈服准则,对岩溶区土洞地基进行安全稳定性判别;WANG.MC等[8]、刘辉等[9]利用上限分析解析法推导条形基础下伏圆形空洞的地基极限承载力上限法解析公式,得到极限承载力的确定方法和确定图表。
综上所述,国内外学者对岩溶区地基承载力课题研究取得了许多富有成效的研究成果,但尚未取得统一的认识,因此,进一步对岩溶区地基承载特性开展研究工作是十分必要的。本文将基于一种新型岩土工程数值方法——上限分析有限元法,对考虑地下空洞影响的岩溶区地基极限承载力确定及影响因素分析作进一步探讨。
1 上限分析有限元法
上限法因具有概念明确、计算简便的特点,已成为一种常用的岩土工程稳定性分析方法,广泛用于求解地基承载力、挡土墙土压力和边坡稳定性等问题[10,11]。对简单的问题,传统上限定理解析法通过构造机动相容的速度场获得对极限荷载的近似估计;但对于复杂荷载条件、几何边界、速度边界和非均质材料等问题,人为构建机动相容的速度场十分困难,上限法的应用因而受到了限制。为克服上述困难,上限分析有限元法应运而生,其核心思想是:利用有限元对速度场进行离散化,然后依据上限定理的相关要求建立相应的约束条件和优化目标函数,得到一个数学规划模型,最后采用数学规划算法求解该模型,从而搜索出连续体破坏时的速度场和极限荷载值。通过将上限定理化归为一个数学规划问题,上限有限元法使得复杂速度场的构建可以交由计算机处理,极大地拓宽了上限法在复杂问题中的应用。数学规划模型的具体形式如下:

上限分析有限元法的计算过程可概括为如下四个主要步骤:计算网格的生成、优化模型的建构、优化模型的求解和计算数据的可视化(图1)。因篇幅所限,上限分析有限元法的相关理论本文不作赘述,详细内容可参考文献[12~15]。

图1 上限分析有限元法求解流程图Fig.1 Solving flowchart of finite element upper bound limit analysis method
2 计算假定与数值计算模型
2.1 计算假定
如图2所示,假定基础宽度为B,其下方存在一直径为D的地下空洞,基础底面与空洞顶部之间的垂直距离为H,地基岩土体的粘聚力、内摩擦角和重度分别为c、φ、γ,则由以上计算参数可以看出,考虑地下空洞影响的岩溶区地基极限承载力的确定所涉及的影响因素众多,是一个非常复杂的问题。为了简化分析计算过程,并突出主要影响因素的作用,提出如下计算假定:
(1)将地下空洞的形状概化为圆形空洞,其位置处于基础的正下方,按平面应变状态计算;
(2)视基础为完全刚性体且底面光滑,基础与土体的接触面上可发生相对位移;
(3)地基岩土体为均质各向同性的理想弹塑性材料,满足关联流动法则;
(4)基础埋置深度为零,不考虑洞内充填物的影响。
需要说明的是,溶洞在漫长的溶蚀发育过程中,其自重应力场处于天然平衡状态,故其破坏主要由外加荷载引起,为此本文在计算中主要研究外加荷载的作用效应。

图2 基础及地下空洞简化基本模型Fig.2 Simplified model of footing and cavity
2.2 上限分析有限元法数值计算模型
根据计算假定及简化基本模型,提出由H/B、D/B和φ共同确定的岩溶区地基极限承载力Pu无量纲公式:

式中:H/B——空洞埋深与其基础宽度之比;
D/B——空洞直径与基础宽度之比。
为全面分析主要影响因素H/B、D/B和φ对岩溶区基础极限承载力的影响,本文在上限分析有限元数值计算时,计算参数取值如下:基础宽度取单位长度,而深度和空洞洞径取基础尺寸的倍数,考虑5种空洞洞径(D/B=1,1.5,2,2.5,3),不同的空洞埋置深度(H/B=1,2,3,4,5),土体参数取 c'=1,φ =0,5,…,35°。为了便于对计算结果进行对比分析,对基础下方无空洞的情况亦进行计算,分析工况全部通算共有208个工况。
因基本模型沿基础中线对称,只需取模型的一半进行计算,图3给出了D/B=2、H/B=2时的上限分析有限元法计算所用网格与边界条件,有限元离散选用线性三角形单元,每个单元含6个节点速度分量和3个应力分量。如图3所示有限元网格共计 2432个单元和 2588个速度间断线。因每一分析工况的洞径和空洞埋置深度有所差异,相应的单元及间断面数也稍有不同。

图3 上限分析有限元法计算网格Fig.3 The mesh of finite element upper bound limit analysis method
3 地基极限承载力计算结果及讨论
3.1 地基极限承载力上限解
根据上述数值计算模型,对208个工况进行上限分析有限元法数值计算,得到岩溶区基础下伏空洞的地基极限承载力上限解Pu/c,将其按同一洞径,不同空洞埋深和内摩擦角绘制地基极限承载力图表,如表1所示,表中符号“-”表示该工况下地基极限承载力等于前一埋置深度的承载力。为便于分析空洞存在的影响,在表中亦给出无空洞时地基极限承载力值作对比。
3.2 地基极限承载力影响因素分析
对比表1中有无空洞工况地基极限承载力值可知,基础下方存在地下空洞时地基极限承载力普遍比无空洞小,表明地下空洞的存在对地基极限承载力产生一定的削弱作用。在同一洞径条件下,地基极限承载力随H/B的增加逐渐增大;当H/B增加到某深度后,地基极限承载力增长渐趋于稳定,接近或达到无地下空洞条件的承载力水平。此时,认为地基极限承载力不受空洞存在的影响,并将该深度视为地下空洞不影响地基极限承载力的临界埋置深度。

表1 D/B=1时地基极限承载力上限解Table 1 Upper bound solution of ultimate bearing capacities when D/B=1
由图4可看出,地基极限承载力随φ变大而增大,且当φ≥10°时,H/B对地基极限承载力影响显著;当含空洞极限承载力曲线与无空洞重合时,说明已达到临界埋置深度要求。进一步分析可看出,当D/B=1时,在H/B=3深度条件下取任意φ值均达到临界埋置深度要求;但洞径D/B=3时,取φ=0~20°时空洞的临界埋置深度为H/B=4,取φ=20~35°时空洞的临界埋置深度为H/B=5,说明空洞的临界埋置深度受D/B和φ的影响。

图4 不同D/B值时地基极限承载力与φ的关系曲线Fig.4 Relation curves of ultimate bearing capacities and φ of different D/B
当H/B=2,3时,地基极限承载力与φ关系曲线如图5所示。从图5中可看出,保持H/B不变,地基极限承载力随洞径D/B的增大而降低,且洞径越大时,地下空洞存在对地基极限承载力削弱越明显;当φ≤10°时,D/B的增大对地基极限承载力的影响较小,当φ>10°时,D/B的增大对地基极限承载力产生显著影响,且φ值越大洞径增加对地基极限承载力降低越明显。分析表明:当空洞具有一定埋置深度时,因岩土体φ值较小,地基极限承载力也较小,地基应力仅在地基浅层土体分布,尚未传至地基深处,地基深处地下空洞大小变化不影响地基极限承载力。而内摩擦角较大时,地基极限承载力随着变大,应力扩散范围变大逐渐传至地下空洞区域,地下空洞大小将对地基极限承载力产生影响。
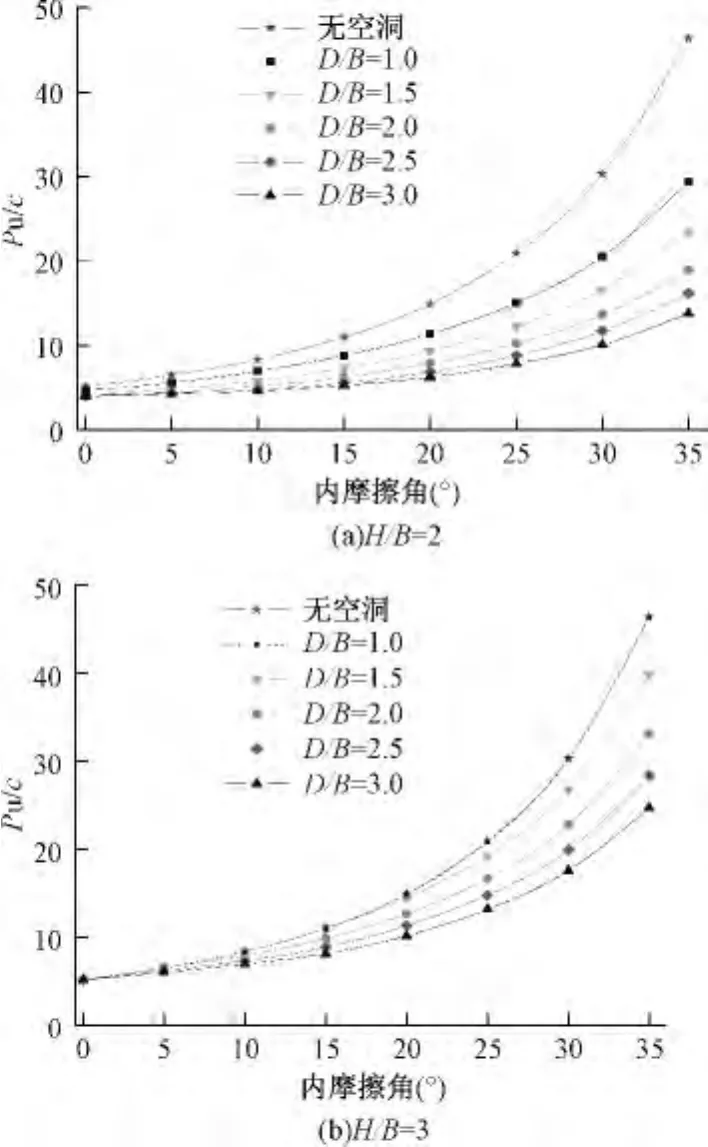
图5 不同H/B值时空洞洞径与极限承载力的关系曲线Fig.5 Relation curves of ultimate bearing capacities and void of different H/B
4 算例分析
4.1 计算参数及结果
本文采用文献[9]的算例,选取基础宽度为B,空洞直径D/B=1~5,空洞埋置厚度H/B=1.0~5.0,c=0.55 MPa,φ =24°,γ =20 kN/m3。按照上述数值计算方法,利用在Matlab平台已编制的计算机程序,对包括无空洞情况下不同空洞埋置深度和直径的地基极限承载力进行计算,将本文计算所得上限解与文献[9]上限解作对比,如表2所示。
4.2 讨论
由表2可知:①采用本文方法计算得到的上限解与文献[9]采用上限分析解析法所获得的上限解很接近;②本文上限解均比文献[9]的上限解小,由塑性理论上限定理可知,本文上限解是一个更接近岩溶区地基极限承载力真实值的上限解。
上述算例对比分析表明,本文运用上限分析有限元法计算得到关于岩溶区地基极限承载力上限解是合理的。通过对算例计算及将计算结果与现有研究成果对比分析,论证了表1岩溶区地基极限承载力上限解对岩溶区类似实际工程的参考价值。在本文方法中无需人为构造机动相容速度场,且能获得较严格上限解,体现了本文方法较现有分析方法的优越性。
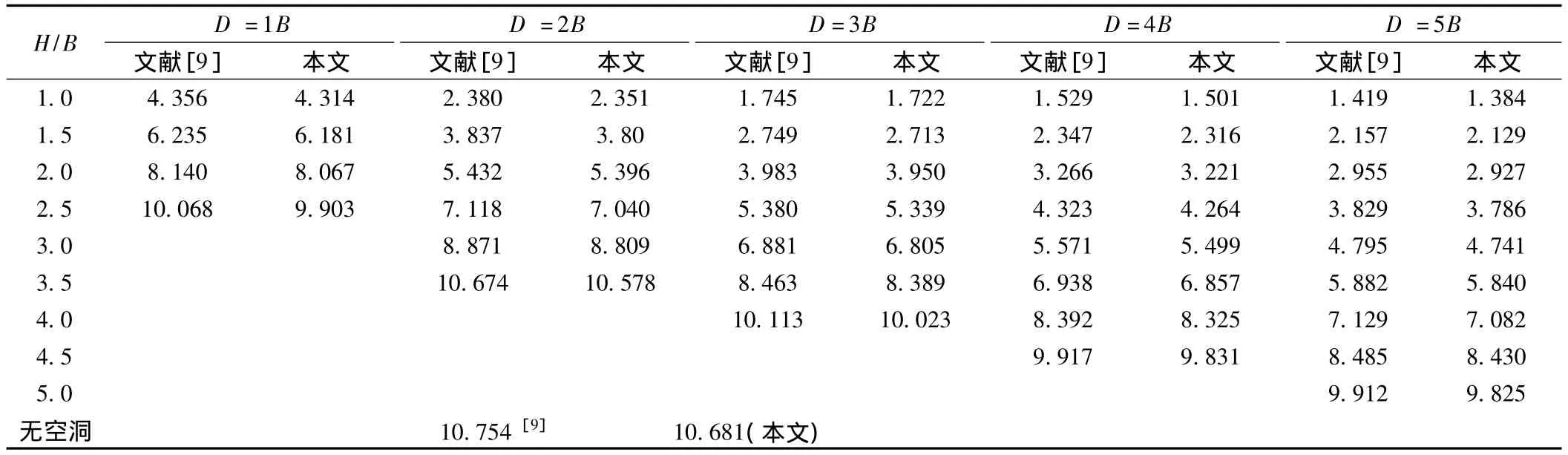
表2 地基极限承载力计算结果(MPa)Table 2 Results of foundation ultimate bearing capacities(MPa)
5 结论
(1)利用上限分析有限元法研究考虑地下空洞影响的岩溶区地基极限承载力确定方法,算例验证了本文方法的合理性,数值计算得出三种因素影响下的地基极限承载力上限解成果数表可为岩溶区基础设计和施工中地基极限承载力的确定提供参考。
(2)通过对岩溶区地基极限承载力影响因素分析表明,地基极限承载力受地下空洞埋置深度、洞径和内摩擦角共同影响;地基极限承载力随D/B增大而减小,随H/B和φ增大而增大;且φ越大,H/B和D/B对地基极限承载力影响效果越显著。
(3)地下空洞在地基中存在一个临界埋置深度,当空洞的埋深超过此临界埋置深度时,可忽略地下空洞对地基极限承载力的影响,该临界埋置深度的大小与D/B和φ有关。
[1] 常士骠,张苏民.工程地质手册[M].4版.北京:中国建筑工业出版社,2006.[CHANG S B,ZHANG S M.Manual of engineering geology[M].4th ed.Beijing:China Architecture and Building Press,2006.(in Chinese)]
[2] Kiyosumi M,Kusakabe O,Ohuchi M.Model Tests and Analyses of Bearing Capacity of Strip Footing on Stiff Ground with Voids[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(4):363-375.
[3] 刘庭金,李元海.有空洞地基破坏过程的试验和数值模拟[J].土工基础,2008,22(2):43-46.[LIU T J,LI Y H.Experimental and Numerical Test on Progressive Failure Process of Clay Foundation with Cavity Below [J].Soil Eng.And Foundation,2008,22(2):43-46.(in Chinese)]
[4] 阳军生,张军,张起森,等.溶洞上方圆形基础地基极限承载力有限元分析[J].岩石力学与工程学报,2005,24(2):296-301.[YANG J S,ZHANG J,ZHANG Q S,et al.Finite element analysis of ultimate bearing capacity of circular footing above karst cave[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(2):296-301.(in Chinese)]
[5] 胡庆国,张可能,阳军生.溶洞上方条形基础地基极限承载力有限元分析[J].中南大学学报(自然科学版),2005,36(4):694-697.[HU Q G,ZHANG K N,YANG J S.Finite element analysis of ultimate bearing capacity of strip footing above Karst cave[J].Journal of Central South University(Science and Technology),2005, 36(4):694-697.(in Chinese)]
[6] 彭芳乐,清住真,高伟,等.空洞的存在对浅基础承载力与沉降影响分析[J].岩石力学与工程学报,2007,26(6):1123-1131.[PENG F L,Kiyosumi Makoto,GAO W,et al.Study on bearing capacity and settlement of shallow foundation with void[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1123-1131.(in Chinese)]
[7] 刘之葵,梁金城,朱寿增,等.岩溶区土洞地基稳定性分析[J].水文地质工程地质,2003,30(3):24-28.[LIU Z K,LIANG J C,ZHU S Z,et al.Stability analysis of soil cave foundation in karst area[J].Hydrogeology& Engineering Geology,2003,30(3):24-28.(in Chinese)]
[8] WANG M C,Hsieh C W.Collapse load of strip footing above circular void[J]. Journal of geotechnical engineering,1987,113(5):511-515.
[9] 刘辉,杨峰,阳军生.空洞上方浅基础地基破坏模式与极限承载力分析[J].岩土力学,2010,31(11):3373-3378.[LIU H,YANG F,YANG J S.Failure mechanism and ultimate bearing capacity of strip footing above void[J].Rock and Soil Mechanics,2010,31(11):3373-3378.(in Chinese)]
[10] CHEN W F.Limit analysis and soil plasticity[M].Amsterdam:Elsevier Science,1975.
[11] 姜玉平,陈征宙,毕港,等.基于极限分析法的边坡临界高度及稳定性研究[J].水文地质工程地质,2012,39(2):43-46.[JIANG Y P,CHEN Z Z,BI G,et al.Research on critical height and stability of slopes based on upperbound limit analysis method[J].Hydrogeology & Engineering Geology,2012,39(2):43-46.(in Chinese)]
[12] Lyamin A V,Sloan S W.Upper bound limit analysis using linear finite elements and non-linear programming[J].International Journal for Numerical and Analytical Methods in Geomechanics,2002,26(2):181-216.
[13] LYAMIN A V,SLOAN S W.Mesh generation for lowerbound limitanalysis [J]. Advances in Engineering Software,2003,34(6):321~338.
[14] Krabbenhoft K,Lyamin A V,Hjiaj M,et al.A new discontinuous upper bound limit analysis formulation[J].International Journal for Numerical Methods in Engineering,2005,63(7):1069-1088.
[15] 王均星,王汉辉,张优秀,等.非均质土坡的有限元塑性极限分析[J].岩土力学,2004,25(3):415-421.[WANG J X,WANG H H,ZHANG Y X,et al.Plastic limit analysis of heterogeneous soil slope using finite elements[J].Rock and Soil Mechanics,2004,25(3):415-421.(in Chinese)]
——太极洞

