变密度声波方程多参数全波形反演策略
杨积忠,刘玉柱,董良国
同济大学海洋地质国家重点实验室,上海 200092
1 引言
地震波全波形反演(FWI)是近30年来发展起来的高分辨率地震数据处理方法.它利用地震观测记录的波形信息提取地下介质的弹性参数(如速度、密度和弹性模量等).全波形反演既可以为偏移成像提供精确的背景速度(刘国峰等,2012),也可以应用到储层定量描述等领域(单蕊等,2011;李国平等,2011),在油气勘探开发中具有重要作用.
由于全波形反演利用了地震波场的全部信息,理论上来讲,应该尽可能多的考虑影响波传播的因素,特别是将大孔径、宽方位数据用于全波形反演时,AVO/AVA效应和方位各向异性效应等需要特别考虑,这就要求将声波近似单参数全波形反演扩展到多参数全波形反演,包括纵横波速度、密度、吸收衰减效应、各向异性参数等.
然而,各参数之间的相互耦合,增加了多参数全波形反演的非线性程度.分析不同参数之间的相互关系,研究不同参数化方式对反演的影响程度,是建立多参数反演策略的有效途径.Tarantola(1986)和Mora(1987)指出,在P波震源反射地震波形反演中,弹性模量是一种比较差的参数化方式;对近偏移距数据(短波长成分)来说,阻抗是相对较好的参数化方式,而对远偏移距数据(长波长成分)来说,速度是比较好的参数化方式,但是,不管利用哪种数据信息,密度都不能被很好地估计.Kohn等(2012)指出,在弹性波多参数波形反演中,不管利用哪种参数化方式,弹性模量、纵横波速度、阻抗都可以被较好地反演出来,而密度反演结果较差;但总的来说,利用速度、阻抗参数化方式得到的反演结果要优于模量参数化方式得到的反演结果.Forgues和Lambaré(1997)通过辐射模式分析指出,密度很难利用全波形反演得到.因此,大部分学者在反演过程中,将密度固定成某一常数或利用速度通过经验关系换算得到密度.
密度是岩石物性参数的重要组成部分,如果能通过反演同时得到比较可靠的纵横波速度、密度资料,这对储层评价、岩性解释和油藏描述等都具有重要作用.弹性波多参数全波形反演的研究实例证明,虽然可以得到相对可靠的纵横波速度,但密度并不能被很好地估计(Choi et al.,2008).因此,需要对密度反演进行深入研究,提出有利于密度反演的多参数全波形反演策略.Jeong等(2012)提出了一种频率域密度反演策略,首先将密度固定为任意常数,通过单参数反演得到弹性模量,进而将换算得到的纵横波速度作为初始模型,再同时反演速度和密度,有效提高了密度的反演精度.Prieux等(2013)先利用大偏移距数据单参数反演速度参数,再利用全偏移距数据同时反演速度、密度参数,有效提高了密度反演的稳定性,但密度反演结果仍然不够理想.他们同时指出,利用速度-密度参数化方式反演得到的速度、密度和阻抗结果要好于利用速度-阻抗参数化方式得到的反演结果.
本文利用速度-密度参数化方式,通过辐射模式及目标函数敏感度分析,研究了速度、密度在反演过程中的相互影响,提出了一种有利于速度、密度同时反演的策略,并通过球状异常模型和 Marmousi-2模型的数值实验验证了该策略的有效性.
2 反演方法简介
全波形反演通过拟合模拟数据umod和观测数据uobs,使波场残差δu达到最小,进而获取地下介质的物性参数m.目标函数可以表达为
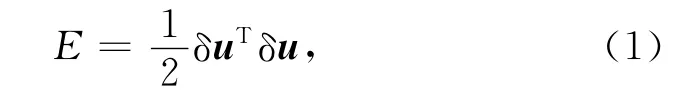
可以利用拟牛顿法更新模型参数mn,使目标函数E达到最小:
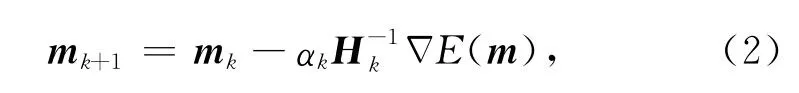
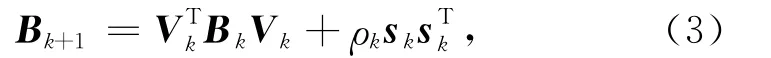
选定某个初始矩阵B0k,对(3)式做m次递推可得:
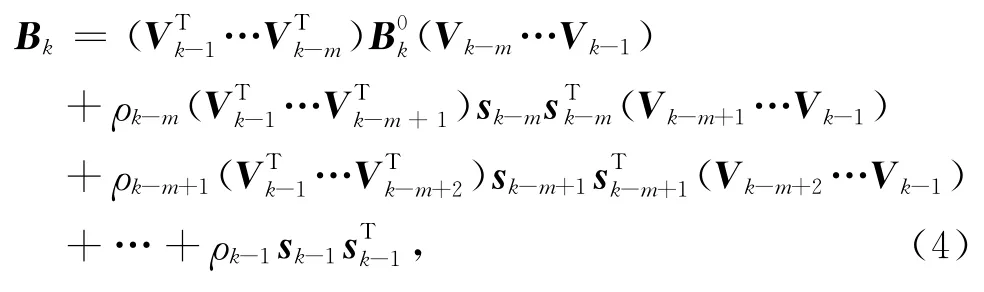
因而,只需记录m(一般取3~20,本文取m=5)个向量对,就可以按公式(4)构造出近似矩阵,具体算法可参考Nocedal and Wright(2006).
频率域变密度声波方程可以表达为
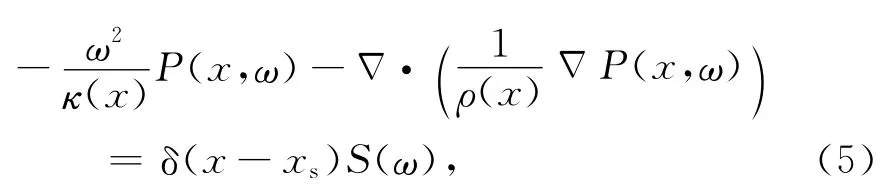
其中,κ为模量,ρ为密度,ω为角频率,P(x,ω)为频率域压力波场,S(ω)是炮点xs处的震源函数.目标函数对模量和密度的梯度可以表达为(Tarantola,1984;Pratt and Worthington,1900)
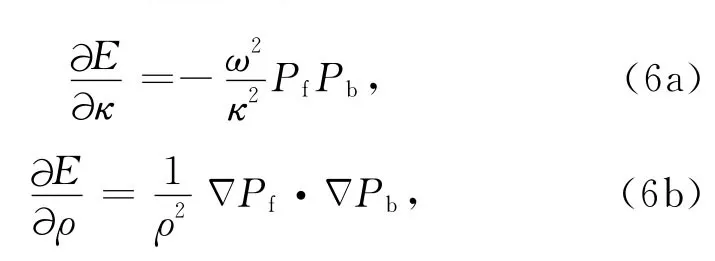
其中,Pf为正传波场,Pb为反传残差波场.梯度可以看成是正传波场和反传残差波场零延迟的互相关,而各参数之间辐射模式的不同导致了梯度在具体表达形式上的差异.
由于模量-密度并不是一种好的参数化方式(Tarantola,1986;Mora,1987;Kohn et al.,2012),本文选取速度-密度为模型参数.目标函数对其它参数的梯度可以利用链式法则(Mora,1987)求得:
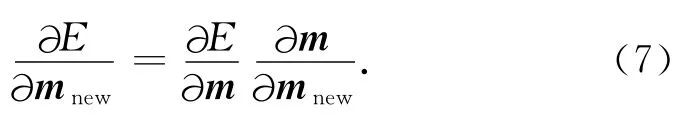
利用模量、速度、密度之间的关系:
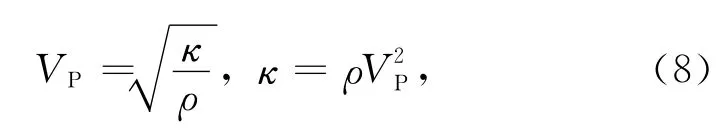
可以得到速度、密度参数化时对应的梯度表达式:
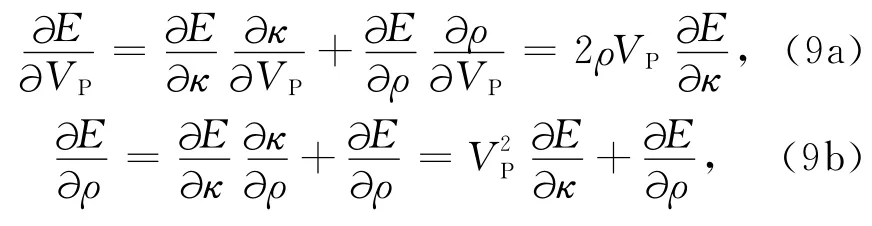
本文的研究都基于公式(9)进行,在具体实验过程中,选取慢度(速度的倒数)和密度的倒数作为模型参数来更新模型(Mulder and Plessix,2004).
3 速度、密度同时反演策略
Forgues和Lambaré(1997)在Ray+Born近似条件下导出了变密度声波方程各种参数化方式对应的辐射模式的数学表达式,并通过对Hessian矩阵的特征值分解分析指出,密度反演比较困难.在Ray+Born近似条件下,速度、密度参数化方式对应的辐射模式如图1所示.
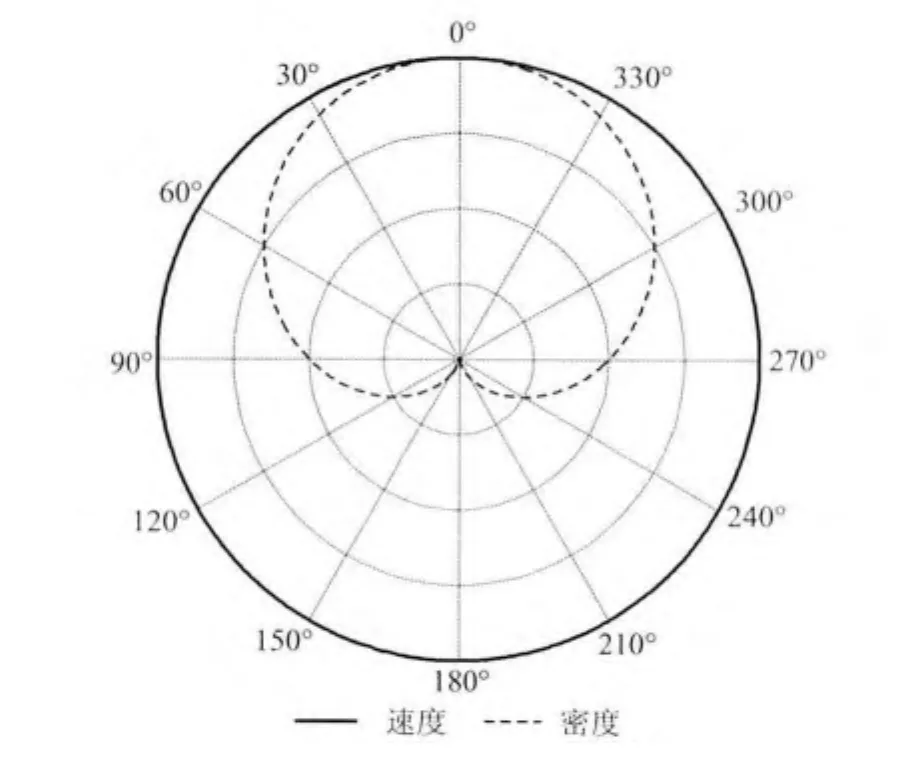
图1 速度-密度参数化方式对应的辐射模式Fig.1 Radiation pattern as a function of diffraction angle for velocity and density
从图1可以看出:(1)速度对应的辐射模式是各向同性的,密度只有在中小角度情况下散射能量,在大角度情况下几乎不散射能量,这说明速度对各种角度信息的数据都比较敏感,但密度只对中小角度的数据敏感;(2)在中小角度情况下,速度、密度的辐射模式基本一致,在这种情况下,速度、密度是耦合在一起的.因此当观测数据中只含有中小角度信息时,要将速度和密度完全区分开来是比较困难的(尽管此时可以得到较好的阻抗信息).
Jannane等(1989)以反射地震数据的L2范数作为目标函数,通过地震波传播正演模拟,得到了目标函数随速度和波阻抗摄动尺度之间的变化关系.结果发现,反射地震数据对速度的长波长成分和阻抗的短波长成分敏感,难以利用地震数据来反演中等摄动尺度的速度信息.董良国等(2013)在此基础上,详细分析了目标函数随不同物性参数(主要为速度和密度)扰动的变化关系,并指出:(1)地震反射波对密度的较小尺度摄动具有很强的敏感度,而中长波长的密度摄动对反射波基本没有影响.根本原因在于密度的摄动不改变地震波的走时,而小尺度的密度摄动会引起反射波振幅的变化,但中长尺度的密度摄动不但不能改变地震波走时,对反射波的振幅也基本没有影响.因此,利用反射波无法反演较大尺度的密度摄动成份;(2)小偏移距反射波可以较好地反演小尺度的波阻抗摄动成份,但要同时反演速度和密度的小尺度摄动可能比较困难,因为小偏移距反射波振幅的变化是小尺度速度摄动和小尺度密度摄动二者共同作用的结果,两者的作用是耦合在一起的;(3)由于密度的中长尺度摄动对反射波基本没有影响,因此,在速度和密度同步扰动的中长尺度摄动区域,目标函数的变化主要是速度的中长尺度摄动引起的;(4)密度摄动的高频成份(小尺度摄动)在不同偏移距反射波上都有很好的反映,增大偏移距,反射波对密度的反演能力有稍许提高;(5)随偏移距的增大,反射波对速度摄动的小尺度成份的反演能力逐渐降低.而大偏移距反射波数据中蕴含着丰富的速度的中长波长信息,有利于反演背景速度(尽管非线性程度较高);(6)大偏移距反射波数据中,由密度的小尺度摄动(高频成份)所引起的目标函数值的变化要远远小于由速度的中长波长摄动所引起的目标函数值的变化.
从上面的分析可以看出,辐射模式分析和目标函数敏感度分析的结论具有较好的一致性.如果直接利用全偏移距、大孔径反射波数据对速度、密度进行同时反演,可以得到速度的各种尺度的摄动成份和密度的高频摄动成份,但由速度的中长波长摄动所引起的目标函数的强烈非线性会严重影响密度的反演结果.前人的研究结果也表明,直接对反射地震数据进行速度、密度同时反演,虽然可以得到比较可靠的速度反演结果,但密度反演结果较差(Choi et al.,2008;Prieux et al.,2013).因此,在进行速度、密度反演的过程中,可以先利用大偏移距数据单参数反演得到速度的中长波长成份,然后再同时对速度、密度进行反演,这是一种比较合理的反演思路.但是,反演过程中无法消除密度的高频摄动对速度反演造成的影响.而且,在具体的实现过程中,速度、密度波长变化的复杂度无法与偏移距的大小建立明确的对应方式,并且反射地震数据中偏移距的大小本来就是一个相对概念,如何有效地将大、小偏移距的数据区分开来成为影响反演结果的重要因素.
因此,本文提出如下的分步反演策略.第一步,利用速度-密度方程同时反演速度和密度,这样可以得到比较可靠的速度反演结果,而密度反演结果较差.第二步,用第一步反演得到的速度作为初始速度模型,舍弃第一步反演得到的密度,利用最初给定的初始密度作为第二步的密度初始模型,继续进行双参数同时反演,这样可以同时得到相对可靠的速度、密度反演结果.为了进一步提高反演精度,可以将第二步反演得到的速度、密度结果作为初始模型,进行下一轮的速度、密度联合反演.
4 数值实验
为了进一步说明速度、密度在反演过程中的相互影响,验证速度、密度分步联合反演策略的有效性,进行如下数值实验.
4.1 速度、密度相互影响
4.1.1 球状异常模型
本节数值实验基于球状异常模型.球状异常体位于均匀背景模型中央,异常体半径100m.速度模型均匀背景值为3000m·s-1,球状异常值为3300m·s-1,密度模型均匀背景值为2000kg·m-3,球状异常值为2200kg·m-3.采用四周观测方式,使得目标体在各个方向的照明均匀,进而消除观测系统的影响.模型纵横向大小为2km×2km,网格离散间距10m.数值模拟152炮数据,记录长度1.5s,时间采样间隔1ms,震源函数选用主频7Hz的Ricker子波.
首先,进行速度(v)、密度(ρ)单参数全波形反演.合成观测数据时,需要反演的模型参数中含有球状异常体,另外一个模型参数为均匀背景模型,初始模型为均匀背景模型.反演结果如图2所示,图3显示的是穿过球状异常体中心的纵向剖面.从图中可以看出,在此种观测方式下,模型各个方向照明均匀,速度、密度反演结果与真实模型非常接近.

图2 单参数全波形反演结果(a)速度;(b)密度.Fig.2 Mono-parameter full-waveform inversion results for velocity(a)and density(b).
接下来,进行速度、密度同时反演,以考察反演过程中速度、密度之间的相互影响.合成观测数据时,其中一个模型参数中含有球状异常体,另外一个模型参数为均匀背景模型.反演过程中所用的初始速度、密度模型为均匀背景模型.
图4显示的是速度含有球状异常体,密度为均匀背景模型时双参数联合反演的结果,图5为穿过球状异常体中心的纵向剖面.很显然,在反演过程中,由速度异常造成的数据残差同时反投影到了速度、密度反演结果当中.从图4和图5中可以看出,速度反演结果与真实模型非常接近,但密度反演结果却远远偏离于真实模型.
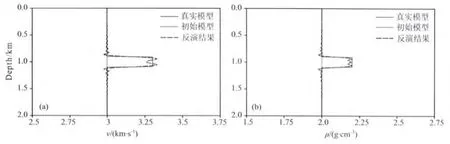
图3 穿过球状异常体中心的单参数反演结果纵向剖面(a)速度;(b)密度.Fig.3 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density
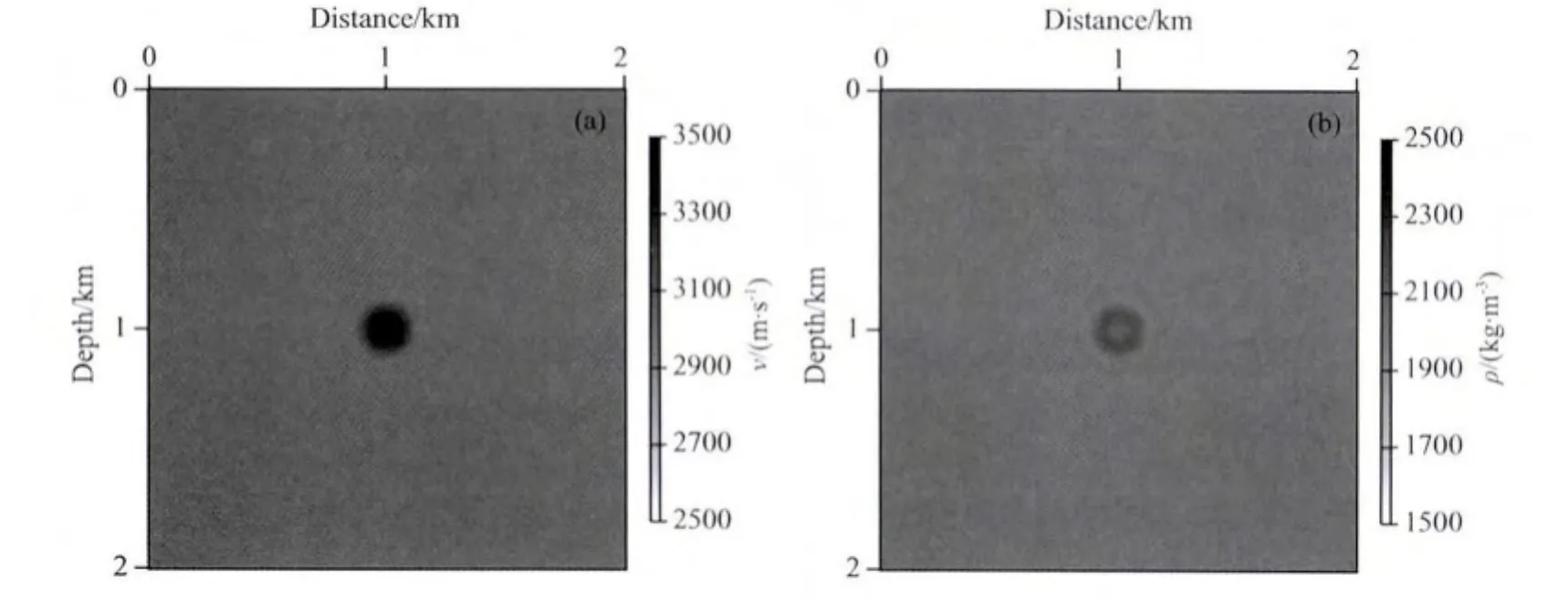
图4 双参数全波形反演结果(a)速度;(b)密度.Fig.4 Multi-parameter full-waveform inversion results for velocity(a)and density(b)
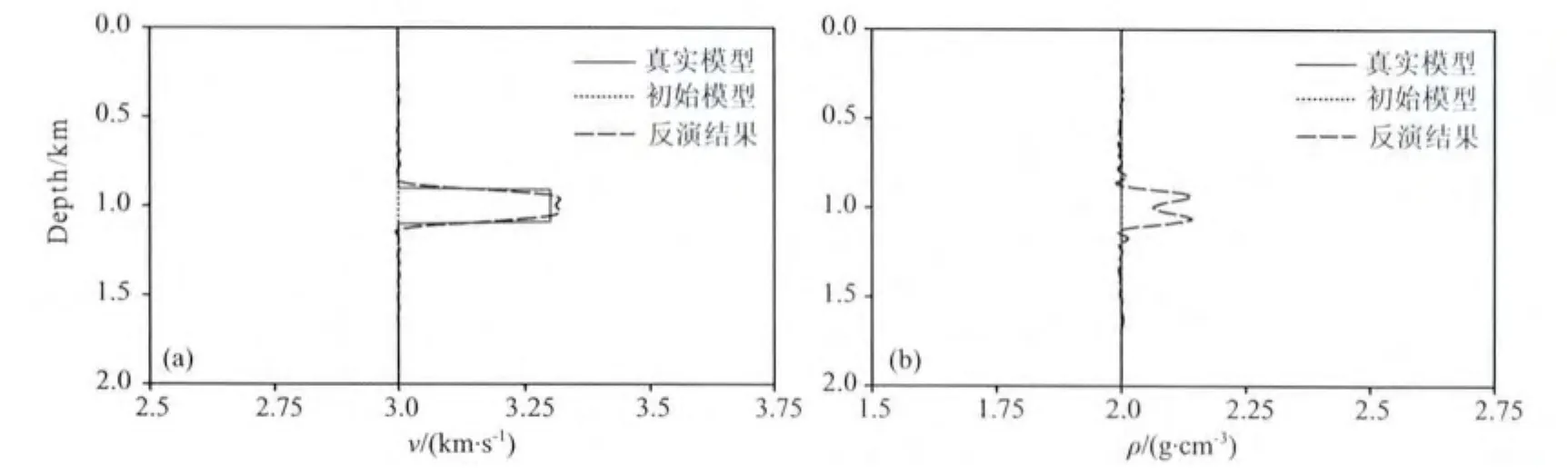
图5 穿过球状异常体中心的双参数反演结果纵向剖面(a)速度;(b)密度.Fig.5 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density
图6 显示的是密度含有球状异常体、速度为均匀背景模型时双参数联合反演的结果,图7为穿过球状异常体中心的纵向剖面.可以发现,在反演过程中,由密度异常造成的数据残差也同时反投影到了速度、密度反演结果当中.从图6和图7中可以看出,速度、密度反演结果都与真实模型比较接近,但密度反演结果分辨率较低,还需进一步的反演.将图6、7与图4、5进行对比,可知速度对密度反演的影响较大,而密度对速度反演的影响相对较小.密度反演依赖于比较可靠的速度信息,而速度的准确反演也离不开有效的密度信息.
4.1.2 Marmousi-2模型
本节数值实验基于 Marmousi-2模型(Martin et al.,2006),横波速度为0,仅反演纵波速度与密度.模型纵横向大小为8km×3.5km,网格离散间距20m.数值模拟79炮数据,第一炮位于地表水平方向100m处,炮间距100m,检波点分布于地表所有网格点上,数据记录长度5.7s,时间采样间隔2ms,震源函数选用主频7Hz的Ricker子波.为了提高计算效率,实验过程中利用了相位编码同步震源技术(Krebs et al.,2009).为了降低同步震源相位编码技术造成的干涉噪声,需要改变每个频率组循环中相位编码的随机数(Krebs et al.,2009),以尽量减少同步震源波场的相干性.
(1)密度对速度反演的影响
首先将密度固定,研究密度在速度反演中所起的作用.真实速度模型和高斯平滑初始速度模型如图8所示.
分别利用以下四种不同密度模型进行单参数(速度)全波形反演:
(1)常密度,密度值为水层密度1010kg·m-3,如图9a所示;
(2)水层密度1010kg·m-3,水层以下密度值为2000kg·m-3,如图9b所示;
(3)高斯平滑初始密度,如图9c所示;
(4)真实密度,如图9d所示;
速度反演结果如图10所示.由图10a可以看出,当密度信息完全不准时,速度反演结果中有许多高频假象,这是因为进行单参数反演时,由密度变化引起的波场残差全部投影到速度反演结果当中,导致速度反演结果较差,特别是有强阻抗界面存在时,这种影响更加明显.由图10(b—d)可以看出,考虑强阻抗界面的影响时,由密度变化引起的波场残差对速度反演的影响并不是特别明显,但这种影响会导致速度反演结果在某些局部地方过高或过低,进而影响速度的后续使用.图11显示了图10(b—d)的纵向速度剖面,可以更清楚的看到这种影响.由此我们可以得知,利用速度、密度参数化方式单参数反演得到的速度结果并不能满足需要,特别是将其用于后续的多参数全波形反演.
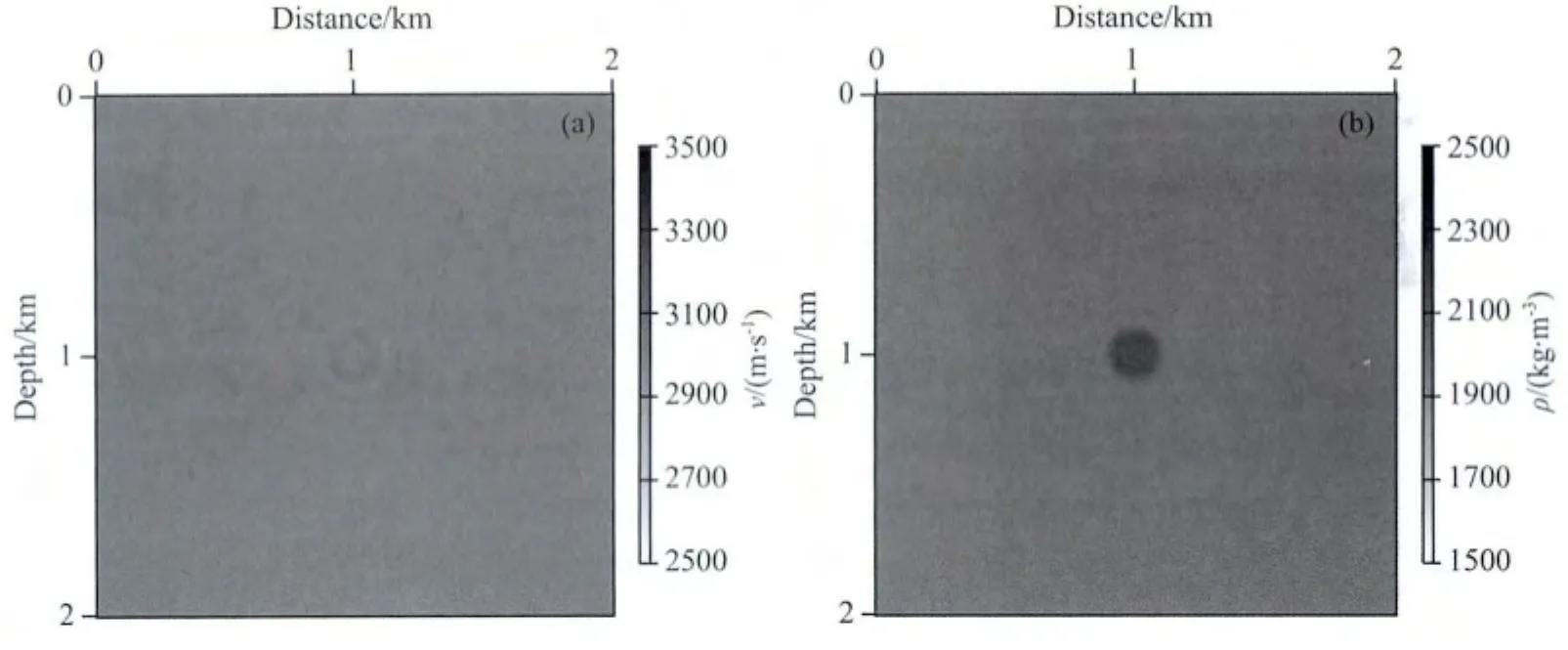
图6 双参数全波形反演结果(a)速度;(b)密度.Fig.6 Multi-parameter full-waveform inversion results for velocity(a)and density(b)
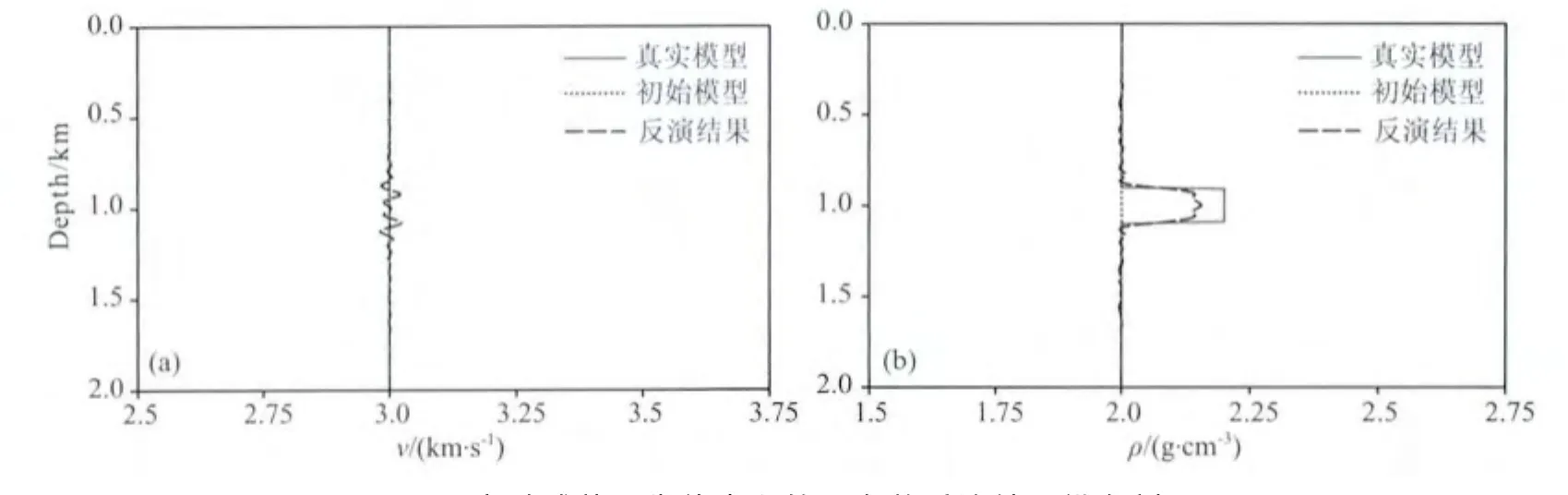
图7 穿过球状异常体中心的双参数反演结果纵向剖面(a)速度;(b)密度.Fig.7 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density

图8 (a)真实速度;(b)高斯平滑初始速度Fig.8 (a)The true velocity model;(b)the Gauss-smoothed initial velocity
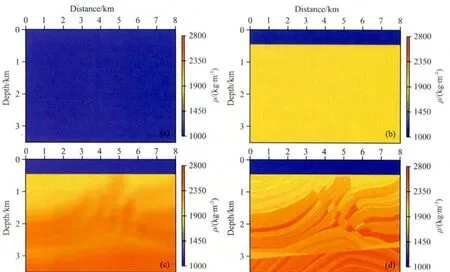
图9 密度模型(a)常密度,密度值为水层密度1010kg·m-3;(b)水层密度1010kg·m-3,水层以下密度值为2000kg·m-3;(c)高斯平滑初始密度模型;(d)真实密度模型.Fig.9 The density model(a)Constant density model which equals 1010kg·m-3;(b)In sediments,density equals 2000kg·m-3,in water,density equals 1010kg·m-3;(c)The Gauss-smoothed initial density model;(d)True density model.
(2)速度对密度反演的影响
将速度固定,研究速度对密度反演的影响程度.真实密度模型和高斯平滑初始密度模型如图12所示.
分别利用图10(b—d)速度模型与图8a所示真实速度模型进行单参数(密度)全波形反演,密度反演结果如图13所示.从图中可以看出,当速度信息准确时,可以得到比较准确的密度反演结果.但是,速度模型的微小变化会引起密度反演结果的巨大变化,并且有可能导致密度反演结果远远偏离真实情况,这说明密度反演依赖于相对可靠的速度信息.图14显示了图13(b—d)的纵向剖面.
4.2 速度、密度分步联合反演策略
由上面的分析可知,密度反演依赖于比较可靠的速度信息,而速度的准确反演也离不开有效的密度信息,单参数反演得到的速度结果并不能用于重建密度模型,需要进行速度、密度分步联合反演.接下来通过如下数值实验,证实本文第3节提出的反演策略的有效性.
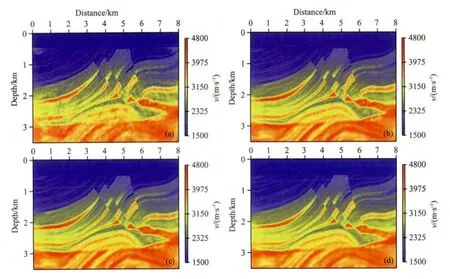
图10 单参数速度反演结果(a)利用图9a密度模型单参数反演得到的速度结果;(b)利用图9b密度模型单参数反演得到的速度结果;(c)利用图9c密度模型单参数反演得到的密度结果;(d)利用真实密度模型单参数反演得到的速度结果.Fig.10 Mono-parameter full-waveform inversion results for velocity(a)The inverted velocity using the density model shown in Fig.9a;(b)The inverted velocity using the density model shown in Fig.9b;(c)The inverted density using the density model shown in Fig.9c;(d)The inverted velocity using the true density model as shown in Fig.9d.
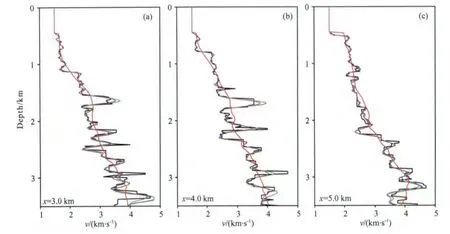
图11 水平方向3km(a)、4km(b)、5km(c)处的纵向速度剖面黑线代表真实速度模型,红线代表初始速度模型,蓝线代表用图9b密度模型单参数反演得到的速度结果,绿线代表用图9c密度模型单参数反演得到的速度结果,粉线代表用真实密度模型单参数反演得到的速度结果.Fig.11 Vertical profiles at horizontal positions of 3km (a),4km (b)and 5km (c)of the inverted results shown in Fig.10The black line indicates the true velocity,the red line denotes the initial velocity,the blue line indicates the reconstructed velocity using the density shown in Fig.9b,the green line denotes the reconstructed velocity using the density shown in Fig.9c,the pink line denotes the reconstructed velocity using the true density.
4.2.1 球状异常模型
本节数值实验基于球状异常模型,模型参数和观测系统设置与4.1.1节完全相同.合成观测数据时,真实速度、密度模型中均含有球状异常体.
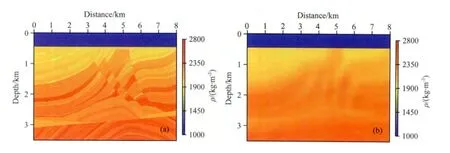
图12 (a)真实密度;(b)高斯平滑密度Fig.12 (a)The true density model;(b)the Gauss-smoothed initial density
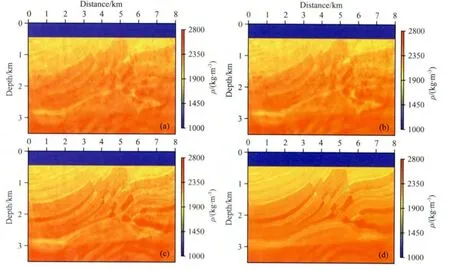
图13 单参数密度反演结果(a)利用图10b速度模型单参数反演得到的密度结果;(b)利用图10c速度模型单参数反演得到的密度结果;(c)利用图10d速度模型单参数反演得到的密度结果;(d)利用真实速度模型单参数反演得到的密度结果.Fig.13 Mono-parameter full-waveform inversion results for density(a)The inverted density using the velocity model shown in Fig.10b;(b)The inverted density using the velocity model shown in Fig.10c;(c)The inverted density using the velocity model shown in Fig.10d;(d)The inverted density using the true velocity model.
首先,利用均匀背景模型作为初始速度、密度模型,对速度、密度进行同时反演.反演结果如图15所示,图16显示了反演结果的纵向剖面.从图中可以看到,速度反演结果与真实模型具有较好的一致性,但密度反演结果却远偏离于真实模型,误差较大.
接下来,将第一步反演得到的速度作为第二阶段的初始速度模型,初始密度模型依然利用均匀背景模型,再一次进行速度、密度联合反演.反演结果和纵向剖面如图17和18所示.从图中可以看到,经过第二阶段的联合反演,可以得到相对比较准确的速度、密度反演结果,但密度反演结果的分辨率不高.
为了进一步提高密度反演精度,利用第二阶段反演得到的速度、密度作为初始模型,进行第三阶段的双参数联合反演.反演结果和纵向剖面如图19和20所示,不难发现,密度反演结果的分辨率较第二阶段有了进一步的提升.
4.2.2 Marmousi-2模型
本节数值实验基于 Marmousi-2模型(Martin et al.,2006),模型参数和观测系统设置与4.1.2节完全相同.为了提高计算效率,实验过程中利用了相位编码同步震源技术(Krebs et al.,2009).为了降低同步震源相位编码技术造成的干涉噪声,需要改变每个频率组循环中相位编码的随机数(Krebs et al.,2009),以尽量减少同步震源波场的相干性.
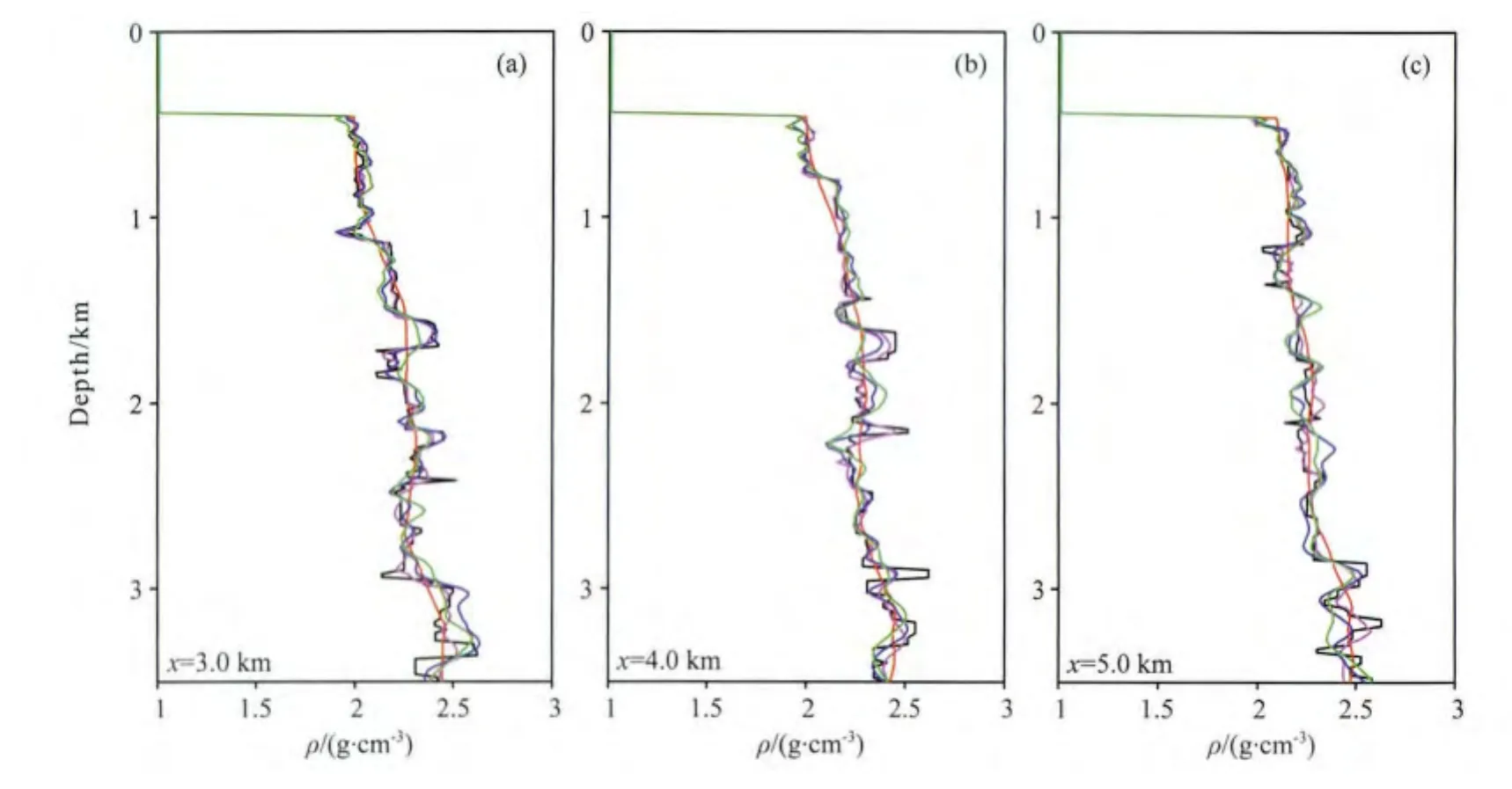
图14 水平方向3km(a)、4km(b)、5km(c)处的纵向密度剖面黑线代表真实密度模型,红线代表初始密度模型,绿线代表用图10c速度模型单参数反演得到的密度结果,蓝线代表用图10d速度模型单参数反演得到的密度结果,粉线代表用真实速度模型单参数反演得到的密度结果.Fig.14 Vertical profiles at horizontal positions of 3km (a),4km (b)and 5km (c)of the models shown in Fig.13The black line indicates the true density,the red line denotes the initial density,the green line denotes the reconstructed density using the velocity shown in Fig.10c,the blue line indicates the reconstructed density using the velocity shown in Fig.10d,the pink line denotes the reconstructed density using the true velocity.
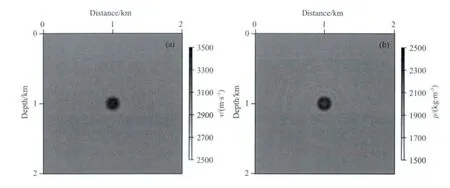
图15 第一阶段双参数全波形反演结果(a)速度;(b)密度.Fig.15 The inverted results in the first stage for velocity(a)and density(b)
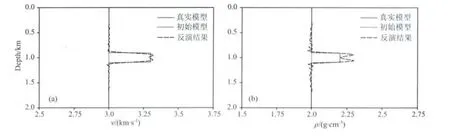
图16 穿过球状异常体中心的第一阶段双参数反演结果纵向剖面(a)速度;(b)密度.Fig.16 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density

图17 第二阶段双参数全波形反演结果(a)速度;(b)密度.Fig.17 The inverted results in the second stage for velocity(a)and density(b)
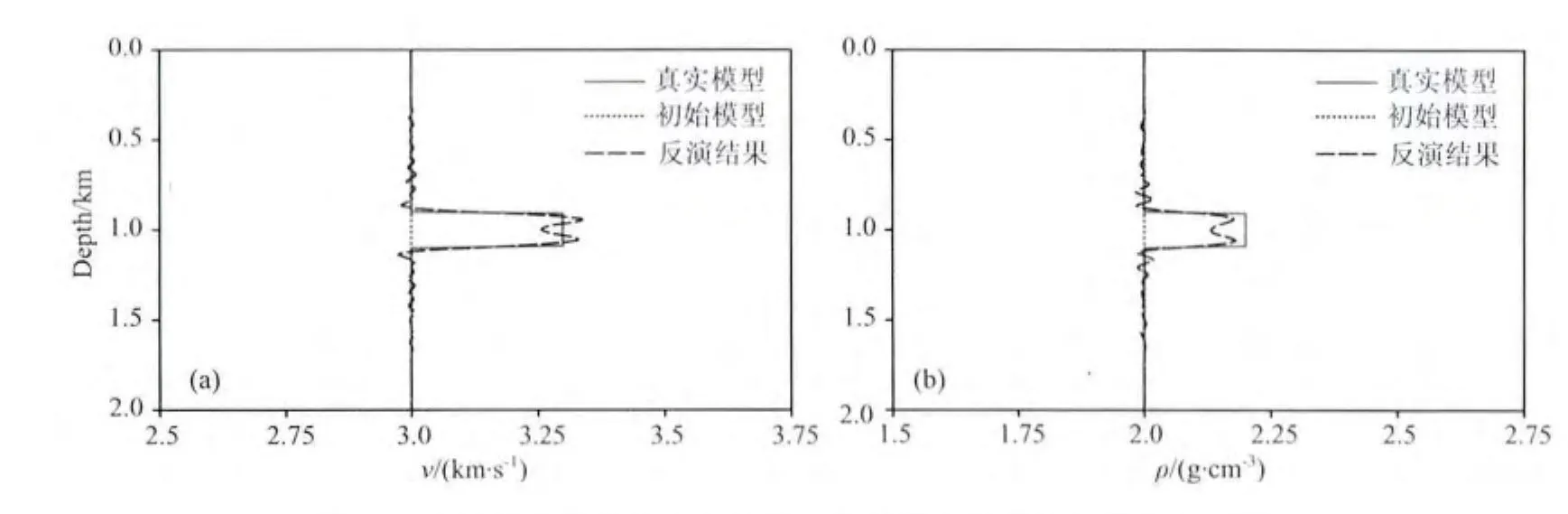
图18 穿过球状异常体中心的第二阶段双参数反演结果纵向剖面(a)速度;(b)密度.Fig.18 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density

图19 第三阶段双参数全波形反演结果(a)速度;(b)密度.Fig.19 The inverted results in the third stage for velocity(a)and density(b)
真实速度、密度模型如图8a和图12a所示,高斯平滑初始速度、密度模型如图8b和图12b所示.首先,利用给定的初始速度、密度模型,对速度、密度进行同时反演.反演结果如图21所示,图22显示了反演结果的纵向剖面.从图中可以看到,虽然密度结果远偏离于真实模型,但速度反演结果与真实模型具有较好的一致性.
接下来,将第一步反演得到的速度作为第二阶段的初始速度模型,初始密度模型依然利用最初给定的初始模型,再一次进行速度、密度联合反演.反演结果和纵向剖面如图23和24所示.从图中可以看到,经过第二阶段的联合反演,可以得到比较准确的速度、密度反演结果,并且第二阶段速度反演结果的分辨率有进一步的提升.
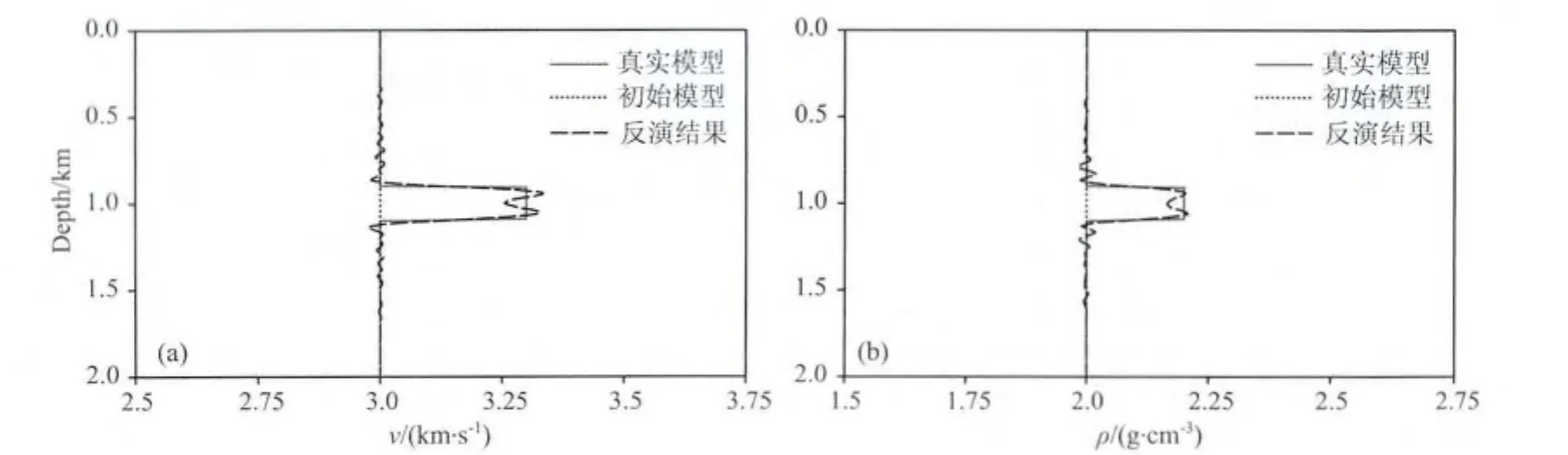
图20 穿过球状异常体中心的第三阶段双参数反演结果纵向剖面(a)速度;(b)密度.Fig.20 Vertical profiles across the center of the inclusion for(a)P-wave velocity and(b)density
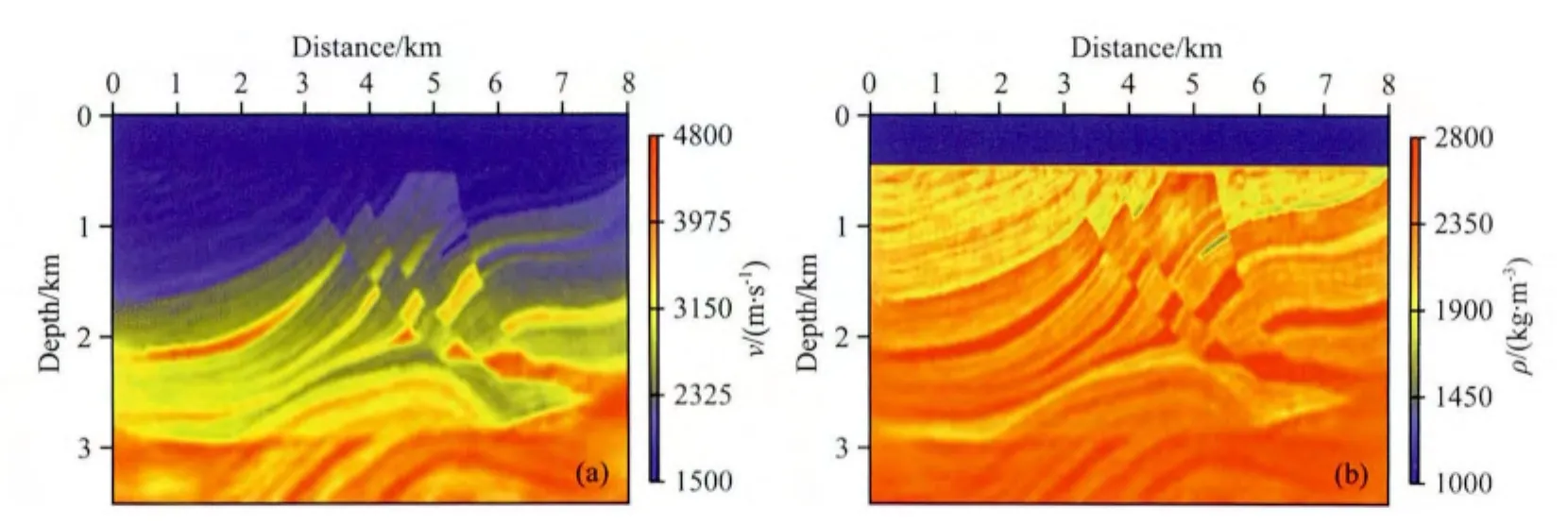
图21 第一阶段双参数反演结果(a)速度;(b)密度.Fig.21 The inverted results in the first stage:(a)P-wave and(b)density
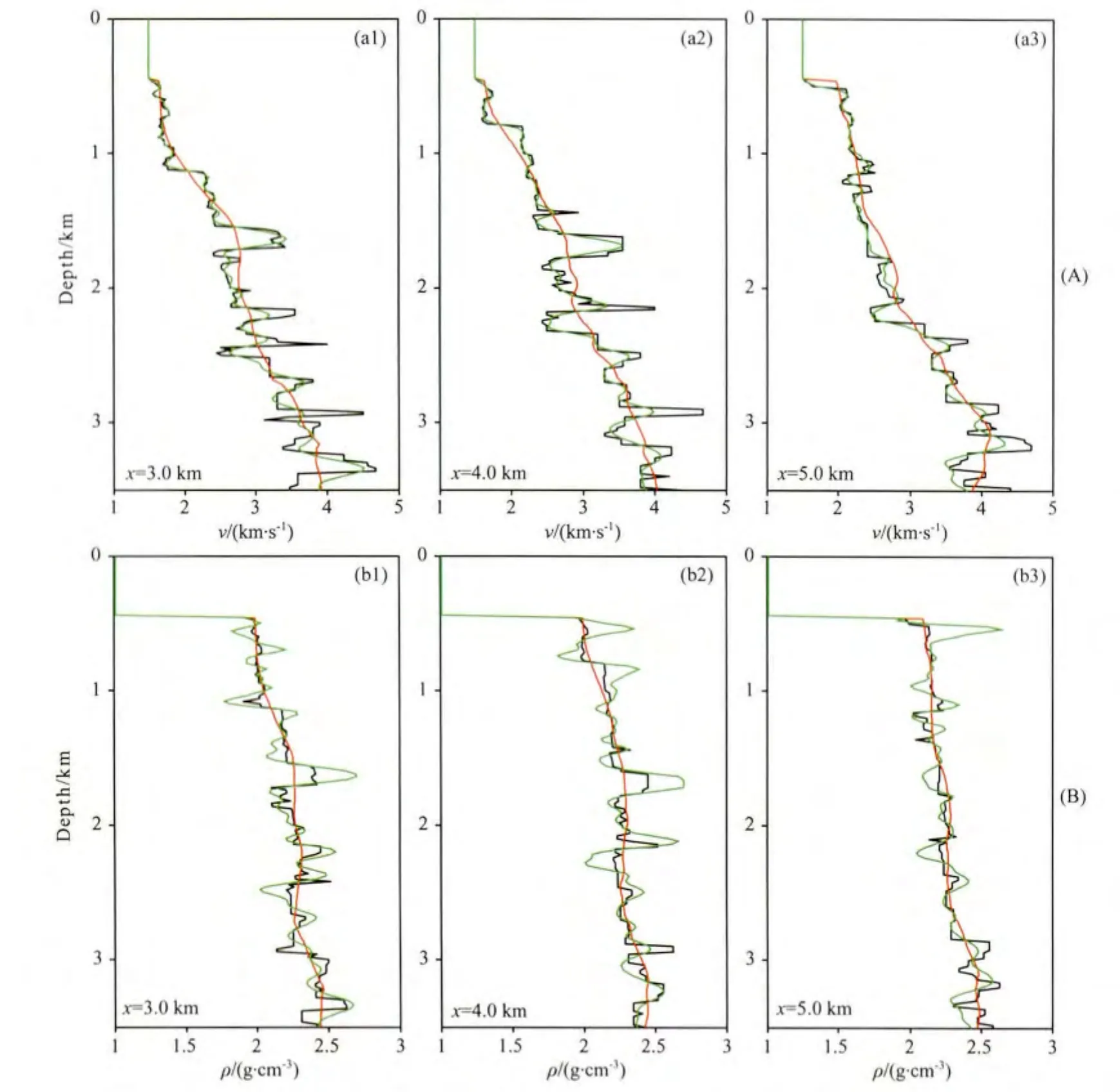
图22 第一阶段双参数反演结果纵向剖面,分别位于水平方向3km(a1,b1)、4km(a2,b2)和5km(a3,b3)处的速度反演结果(A)与密度反演结果(B)黑线代表真实模型,红线代表初始模型,绿线代表反演结果.Fig.22 Vertical profiles at horizontal positions of 3km (a1,b1),4km (a2,b2)and 5km (a3,b3)of the models shown in Fig.21for P-wave velocity(A)and density(B)The black line indicates the true model,the red line denotes the initial model and the green line denotes the reconstructed model.
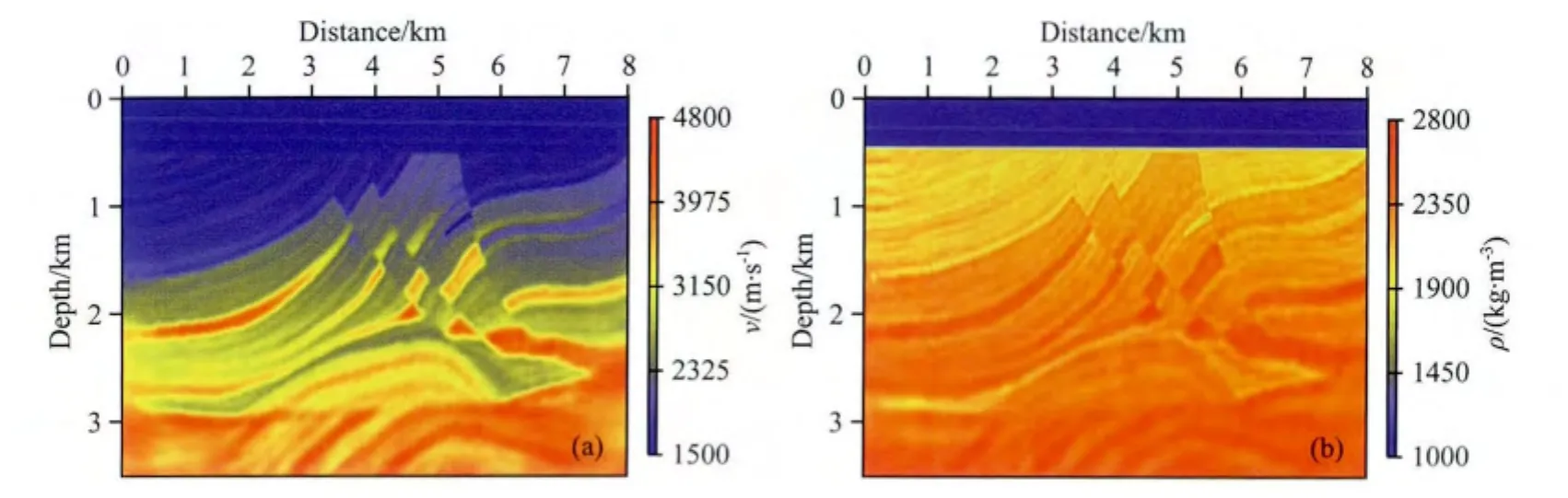
图23 第二阶段双参数反演结果(a)速度;(b)密度.Fig.23 The inverted results in the second stage:(a)velocity;(b)density
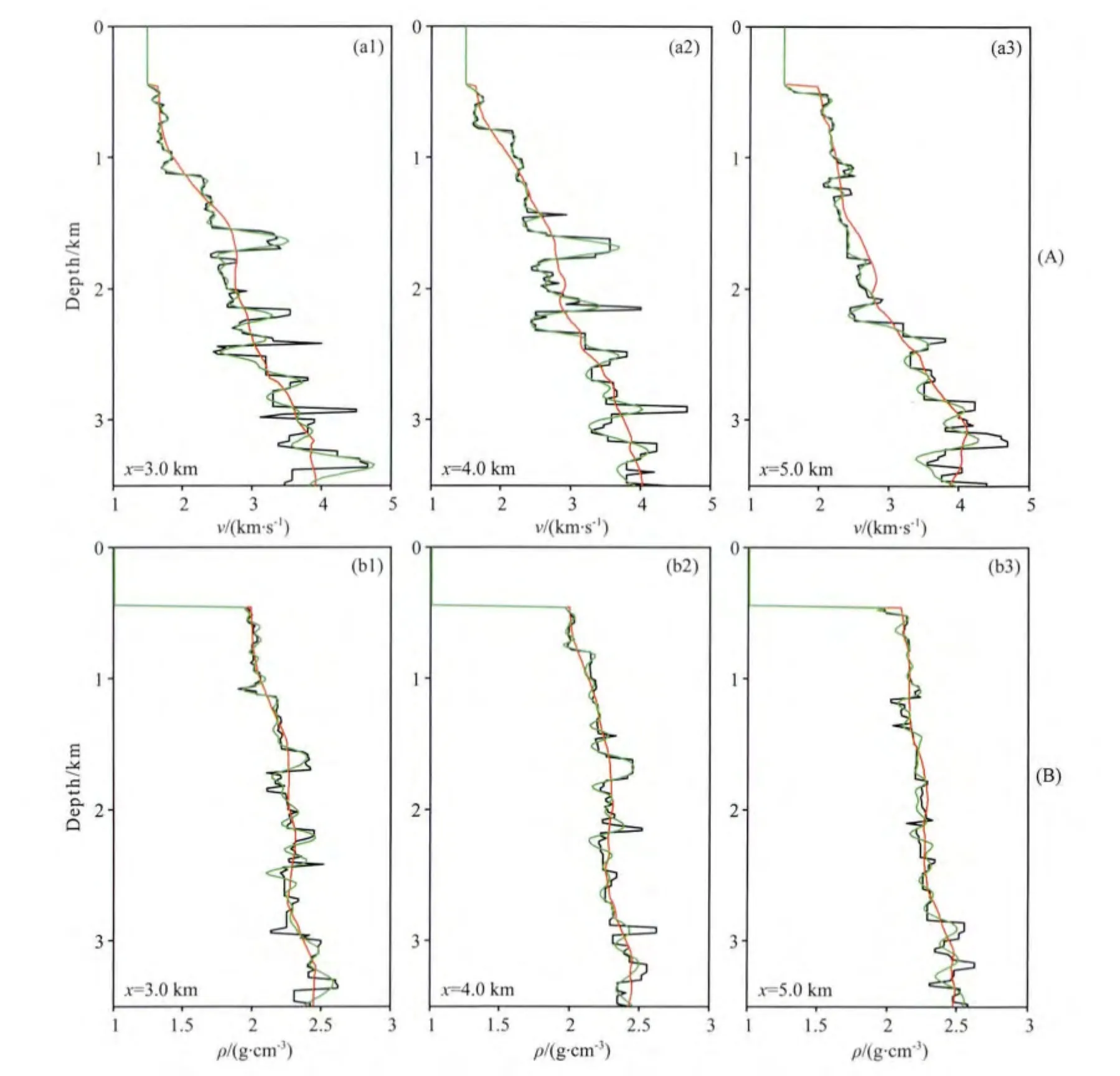
图24 第二阶段双参数反演结果纵向剖面,分别位于水平方向3km(a1,b1)、4km(a2,b2)和5km(a3,b3)处的(A)速度反演结果与(B)密度反演结果黑线代表真实模型,红线代表初始模型,绿线代表反演结果.Fig.24 Vertical profiles at horizontal positions of 3km (a1,b1),4km (a2,b2)and 5km (a3,b3)of the models shown in Fig.23for(A)P-wave velocity and(B)densityThe black line indicates the true model,the red line denotes the initial model and the green line denotes the reconstructed model.
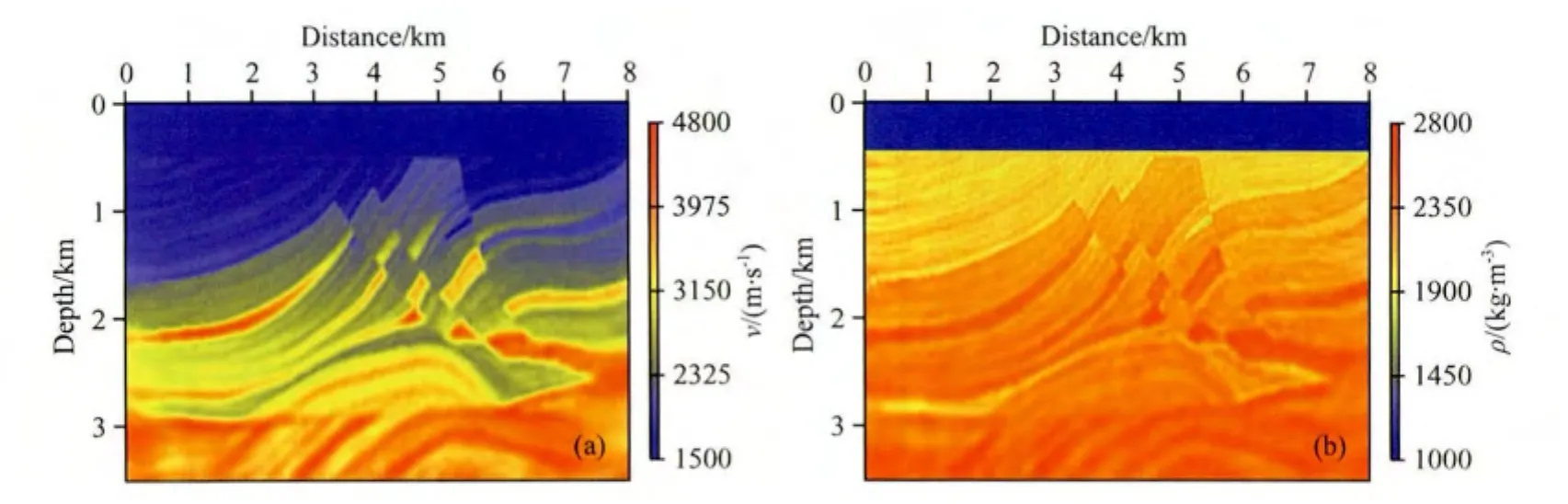
图25 第三阶段双参数反演结果(a)速度;(b)密度.Fig.25 The inverted results in the third stage:(a)velocity;(b)density
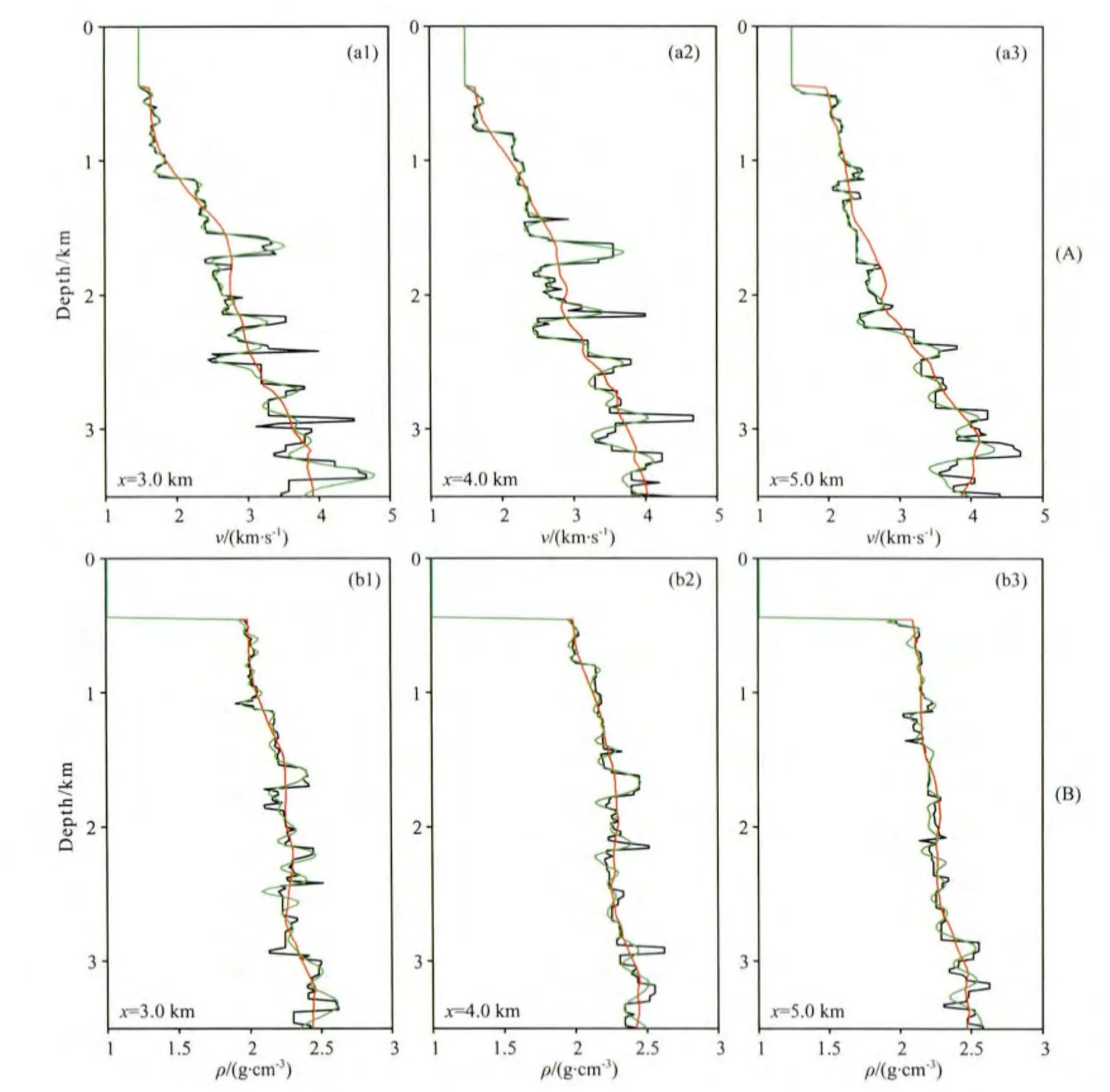
图26 第三阶段双参数反演结果纵向剖面,分别位于水平方向3km(a1,b1)、4km(a2,b2)和5km(a3,b3)处的(A)速度反演结果与(B)密度反演结果黑线代表真实模型,红线代表初始模型,绿线代表反演结果.Fig.26 Vertical profiles at horizontal positions of 3km (a1,b1),4km (a2,b2)and 5km (a3,b3)of the models shown in Fig.25for(A)P-wave velocity and(B)densityThe black line indicates the true model,the red line denotes the initial model and the green line denotes the reconstructed model.
从图21—24可以看出,进行分步多参数全波形反演,可以得到比较好的速度、密度反演结果,接下来进行第三阶段的多参数联合反演,看是否可以进一步提高反演精度.此时,利用第二阶段反演得到的速度、密度结果作为第三阶段的初始模型.第三阶段的反演结果和纵向剖面如图25和26所示.不难发现,密度反演结果的分辨率较第二阶段有了进一步的提升,但提升空间有限,主要是由于第二阶段密度反演结果已非常接近真实模型.
5 结论与讨论
反演策略对多参数全波形反演至关重要.本文通过数值实验证实,密度反演依赖于比较可靠的速度信息,而速度的准确反演也离不开有效的密度信息.固定密度,单参数反演得到的速度往往并不能满足后续对速度的进一步要求.因此,本文提出了有利于速度、密度同时反演的策略.该策略充分考虑了多参数全波形反演中目标函数对速度、密度的敏感性差异,分步实现对速度、密度的反演,在一定程度上降低了多参数全波形反演的非线性程度.第一步,利用给定的初始模型对速度、密度进行同时反演.此时,可以得到相对可靠的速度反演结果,而密度反演结果较差.第二步,将第一步反演得到的速度作为第二步的初始速度模型,舍弃第一步反演得到的密度,利用最初给定的密度作为第二步的初始密度模型,进行双参数同时反演,这样可以同时得到比较可靠的速度、密度反演结果.为了进一步提高反演精度,可以将第二步反演得到的速度、密度作为初始模型,继续进行下一轮的双参数同时反演.数值实验证实了该策略的有效性.尽管本文是基于变密度声波方程研究多参数全波形反演策略,但该策略同样可以应用到弹性波或各向异性的多参数全波形反演中.
Choi Y,Min D J,Shin C.2008.Two-dimensional waveform inversion of multi-component data in acoustic-elastic coupled media.GeophysicalProspecting,56(6):863-881.
Dong L G,Chi B X,Tao J X,et al.2013.Objective function behavior in acoustic full-waveform inversion.ChineseJ.Geophys.(in Chinese),56(10):3445-3460.
Forgues E,LambaréG.1997.Parameterization study for acoustic and elastic ray+ Born inversion.JournalofSeismic Exploration,6:253-277.
Jannane M,Beydount W,Crase E,et al.1989.Wavelengths of Earth structures that can be resolved from seismic reflection data.Geophysics,54(7):906-910.
Jeong W,Lee H Y,Min D J.2012.Full waveform inversion strategy for density in the frequency domain.Geophys.J.Int.,188(3):1221-1242.
Kohn D,De Nil D,Kurzmann A,et al.2012.On the influence of model parametrization in elastic full waveform tomography.Geophys.J.Int.,191(1):325-345.
Krebs J,Anderson J,Hinkley D,et al.2009.Fast full-wavefield seismic inversion using encoded sources.Geophysics,74(6):WCC177-WCC188.
Li G P,Yao F C,Shi Y M,et al.2011.Pre-stack wave equation inversion and its application in frequency domain.OGP,46(3):411-416.
Liu G F,Liu H,Meng X H,et al.2012.Frequency-related factors analysis in frequency domain waveform inversion.ChineseJ.Geophys.(in Chinese),55(4):1345-1353.
Mart in G S,Wiley R,Marfurt K J.2006.Marmousi2—an elastic upgrade for Marmousi.TheLeadingEdge,25(2):156-166.Mora P R.1987.Nonlinear two-dimensional elastic inversion of multi-offset seismic data.Geophysics,52(9):1211-1228.
Mulder W A,Plessix R E.2004.A comparison between one-way and two-way wave-equation migration.Geophysics,69(6):1491-1504.
Nocedal J,Wright S J.2006.Numerical optimization.Springer Science+Business Media,LLC.
Prat t R G,Worthington M H.1990.Inverse theory applied to multisource cross-hole tomography,Part 1:Acoustic waveequation method.GeophysicalProspecting,38(3):287-310.
Prieux V,Brossier R,Operto S,et al.2013.Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field.Part 1:imaging compressional wave speed,density and attenuation.Geophys.J.Int.,194(3):1640-1664.
Shan R,Bian A F,Yu W H,et al.2011.Pre-stack full waveform inversion for reservoir prediction.OilGeophysical Prospecting,46(4):629-633.
Tarantola A.1984.Inversion of seismic reflection data in the acoustic approximation.Geophysics,1984,49(8):1259-1266.
Tarantola A.1986.A strategy for nonlinear inversion of seismic reflection data.Geophysics,51(10):1893-1903.
附中文参考文献
董良国,迟本鑫,陶纪霞等.2013.声波全波形反演目标函数性态.地球物理学报,56(10):3445-3460.
李国平,姚逢昌,石玉梅等.2011.频率域叠前波动方程反演及其应用.石油地球物理勘探,46(3):411-416.
刘国峰,刘洪,孟小红等.2012.频率域波形反演中与频率相关的影响因素分析.地球物理学报,55(4):1345-1353.
单蕊,卞爱飞,於文辉等.2011.利用叠前全波形反演进行储层预测.石油地球物理勘探,46(4):629-633.
——工程地质勘察中,一种做交叉剖面的新方法

