基于广义Hamilton系统的机械人双目视觉伺服控制器*
邹立颖 ,朱 磊 ,苗凤娟 ,杨 波
(1.齐齐哈尔大学 通信与电子工程学院,黑龙江 齐齐哈尔 161006;2.山西大学 数学科学学院,山西 太原 030000)
近年来,机器人视觉伺服控制成为机器人领域内研究的热点之一[1-2]。视觉伺服是利用视觉传感器获得目标物体的图像信息作为反馈信号,对机器人进行闭环控制[3]。目前视觉伺服控制所面临的主要问题是全局渐近稳定性、物体深度信息的获取、干扰抑制、系统镇定、控制精度等问题。
广义Hamilton系统的Hamilton函数是系统的总能量,在一定条件下可构成系统的李亚普诺夫函数。因此,关于广义Hamilton系统理论的研究得到了研究人员的广泛关注[4-5]。参考文献[5]开发了一种新的数学工具,构建了机器人系统广义Hamilton框架,为广义Hamilton系统在机器人控制领域的发展奠定了基础。参考文献[6]研究了基于图像的直接视觉伺服控制器的设计与仿真。参考文献[7]基于机器人动力学特性和位置的视觉反馈信息,建立了一类视觉反馈控制系统。但参考文献[7]中由于考虑了机器人动力学特性,李亚普诺夫函数的设计过于复杂,导致系统稳定性分析较困难。而广义Hamilton系统可以克服参考文献[7]的不足。因此,本文基于广义Hamilton系统理论,研究了视觉伺服控制器设计问题。
本文基于参考文献[6]提出的双目视觉模型,考虑机器人动力学特性,在参考文献[5]的基础上构建了广义哈密尔顿视觉伺服系统(GHVFS)。针对GHVFS,提出了基于广义Hamilton框架下的视觉伺服控制器设计方法。该方法采用的视觉模型无需获取深度信息,也不需要物体的模型,简化了控制器结构。选用Hamilton函数为李亚普诺夫函数,使系统稳定性分析变得简单。对于GHVFS下的L2增益干扰抑制问题,提出了具有L2增益性能视觉伺服控制器,给出了闭环系统稳定性证明。最后给出的仿真实验验证了该方法的可行性和有效性。
1 视觉模型
[6]提出的双目视觉模型如下[6]:
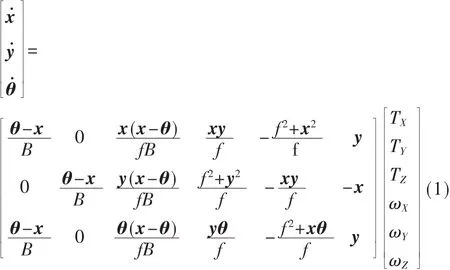
mi=[x y c]T为目标物体的第i个特征点,vC=[TXTYTZ]T为摄像机线速度,ωC=[ωXωYωZ]T为摄像机角速度,摄像机运动速度VC=[vTcwTc]T,图像特征点速度m˙i与 VC满足:

其中,Ji(mi)∈R3×6表示特征点mi的图像雅克比矩阵。
机械手关节速度与终端速度的关系:

其中,J(q)为机械手雅克比矩阵,q∈Rn为关节位置向量。
具有n个特征点的物体图像速度与关节速度关系为:

其中m=[mT1mT2…mTn]T为物体图像特征向量,J(m)=[JT1(m1) JT1(m2)…JTn(mn)]T为物体的图像雅克比矩阵,(m,q)=J(m)J(q)为物体复合雅克比矩阵。
2 机器人动力学模型
机械人动力学模型为:

其中τ∈Rn为关节输入力矩向量,M(q)为正定对称的惯性矩阵,C(q,q˙)为非线性离心力项,G(q)为重力矩向量。
3 双目视觉伺服系统的广义Hamilton框架
为建立双目视觉伺服系统下的广义Hamilton框架,给出如下命题:
命题1[5]:

系统(5)变为:

命题2[5]:
系统(6)对下列关系对任意的p∈Rn和 q∈Rn成立:

其中 En(i,j)∈Rn×n为交换矩阵,(j-1)n+i]。
取系统Hamilton函数为:

其中q∈Rn是关节位置向量,p=M(q)˙是系统的广义动量,m*为期望图像特征向量,m为图像特征向量,φ1和φ2为相应维数的系数矩阵,β是与G(q)的不确定部分相关联的未知向量,是 β的估计。
对式(8)求导得:

由 p=M(q)q˙得 :
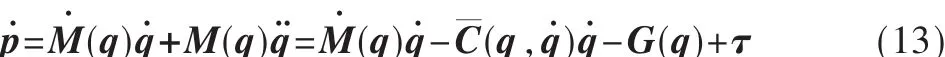
假设G(q)的不确定部分线性地依赖于未知向量β∈Rl,即存在矩阵 φ(q)∈Rn×l使得 G(q)=G0(q)+φ(q)β,G0(q)∈Rn表示G(q)的标称部分。
为构建广义Hamilton框架,设计反馈律:

其中u∈Rn为新的控制输入,KD=KTD∈Rn×n。
将(7)、(14)代入(13)中得:

自适应估计律为:

式(9)、(15)、(16)构成了 GHVFS 系统的机器人动力学特性部分。
在机械手末端端速度中引入一个新的控制输入:
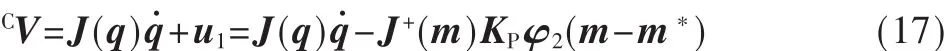
其中,u1∈Rn是新的控制输入,J+(m)是 J(m)的广义逆矩阵。
将(17)代入(4)中,再由(10)、(12)式得 GHVFS 系统的视觉伺服部分:

其中KP=KTP∈Rm×m。
由式(9)、(15)、(16)、(18)得到 GHVFS 系统:


4 L2控制器设计
考虑不确定性,双目视觉伺服系统的广义哈密尔顿实现为:

其 中 ,g2(X)=[0 In0 0]T∈R(2n+l+m)×b,h(X)是 权 重 矩 阵 ,X∈R2n+l+m,u∈RS,ω∈L2为等值干扰信号,y∈RP是输出,z∈Rq是罚信号。
定义:考虑系统(21)及 γ 供给率 s(ω,z)=(1/2)(γ2||ω||2-||z||2),||ω||、||z||均指向量的欧几里得范数, 对于 γ>0,若存在控制律u及半正定的光滑存储函数H,使得耗散不等式H˙≤(γ2||ω||2-||z||2)对于任意的干扰 ω 成立,则称该系统是γ耗散的[8]。
由于系统的γ耗散性与L2性能之间关系是等价的[9]。L2性能准则设计问题可以叙述如下:对于给定系统(21),设计控制器 u,使得闭环系统对任意正数 γ,满足如下性能准则:
(1)当ω=0时,闭环系统在平衡点m*处是渐近稳定的。
(2)存在半正定存储函数 H(X),对于任意干扰 ω,使得耗散不等式成立。
(3)闭环系统在图像平面期望特征点m*是可检测的。

满足准则(1)、(3)的控制律为:
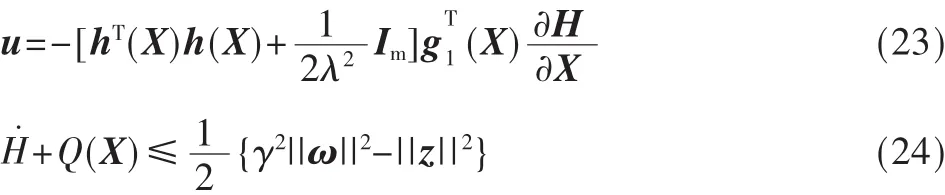
证明:
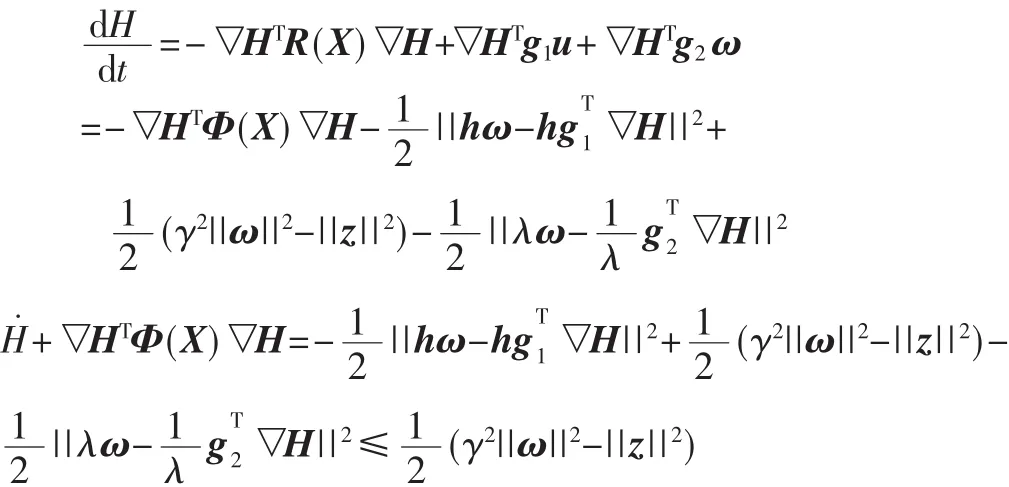
又由 Φ(X)≥0,所以 Q(X)=▽HTΦ(X)▽H≥0。根据定义 1及 γ耗散性与 L2性能等价性可得,控制律(23)是系统(21)的一个L2干扰抑制控制器。
定理 2:假设 ω=0,由式(14)、式(23)、式(21)构成的闭环系统在目标平衡点Xe=[q 0β(m*)T]是渐近稳定的。
证明:由 H(X)的构成可知,H(X)正定并且在平衡点Xe取得严格极小。
当 ω=0 时,由式(22)及(24)得:

因此,闭环系统稳定且收敛于包含在下列集合内的最大不变集上。

当∀t≥0时,由于z=hgT1▽H=0,h(X)列满秩,y=gT2▽H=0,可得≡0,≡0。即p(t)=M(q)q˙=M(q)≡0,由≡0知 φ(m-m*)=0,又由φ正定,所以 m=m*,即▽H(X(t))=▽HX(t))=0,∀X∈S。 因此,S 中仅包含一个点Xe,由LaSalle不变原理得闭环系统渐近稳定。
5 系统仿真试验
为验证本文所提出的方法,采用图1所示两关节机械手视觉伺服系统进行仿真分析。

图1 带有两个摄像机的2DOF机器人系统
考虑具有不确定性的两关节机械手动力学方程:
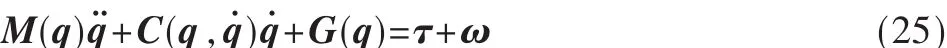
取矩形图形顶点为目标的特征点,初始位置图像坐标为m1=[44.755 1;71.737 3;-44.755 1]pixels,m2=[-44.755 1;71.737 3;-134.265 2]pixels,m3=[-44.755 0;-17.772 9;-134.265 2]pixels,m4=[44.755 1;-17.772 9;-44.755 1]pixels。期望位置图像坐标为 m1*=[68.448 9;27.182 1;-68.448 9]pixels,m2*=[-68.448 9;27.182 1;-205.346 8]pixels,m3*=[-68.448 9;-109.715 8;-205.346 8]pixels,m4*=[68.448 9;-109.715 8;-68.448 9]。 q1(0)=0°,q2(0)=90°,(0)=0,(0)=0,ω=[20sin(t)20sin(t)]T,γ=0.252,KD=diag{0.1,0.8},h(X)=diag{0.05,0.05}。
图2~图7为目标深度在摄像机坐标系中变化时的仿真结果。图2表示图像误差渐近收敛到零,表明特征点在图像平面的位置收敛到期望位置。图3表示了摄像机的运动轨迹。图4为机械手的运动轨迹,机械手的初始状态为 q1=0°,q2=90°。图 5为不确定参数的变化曲线。图6~图7分别为左、右摄像机在像平面的运动轨迹。由仿真结果可以看出,在存在不确定性干扰的前提下,所设计的控制器能够使当前图像特征渐近收敛于期望图像特征,图像误差逐渐趋近于零,即机器人运动到期望位置。
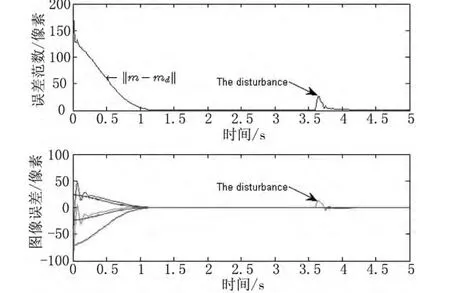
图2 特征点误差范数

图3 摄像机运动轨迹立体图

图4 机械手运动轨迹图
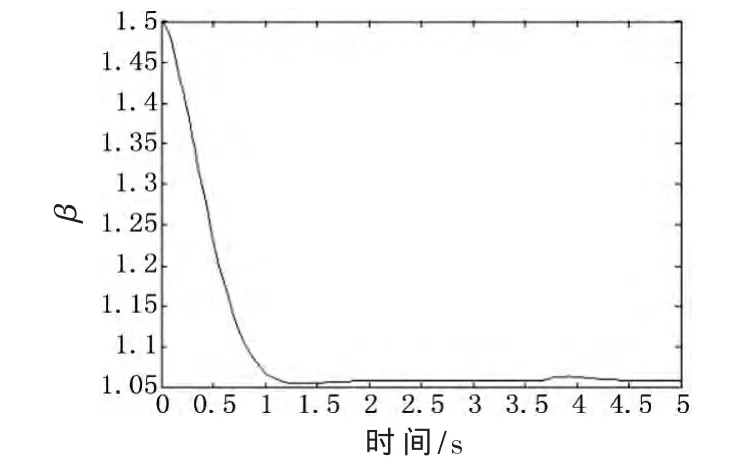
图5 不确定参数β的变化曲线

图6 左摄像机平面目标运动轨迹

图7 右摄像机平面目标运动轨迹
对于手眼机器人,考虑动力学特性构造了视觉伺服系广义哈密尔顿系统,本文提出了一种新的视觉伺服控制器,能够使机械手稳定地收敛到期望位置,解决了视觉伺服控制的干扰抑制问题。本设计将广义Hamilton理论应用到视觉伺服控制器设计中,构造了GHFVS模型,将系统的Hamilton函数用作李亚普诺夫函数,使得稳定性分析和控制器设计简单。此外,所采用的视觉模型中不需要获取深度信息,简化了控制器结构。理论分析和实验均证明了该方法具有全局渐近稳定性、鲁棒性和快速性等控制性能。
参考文献
[1]邹立颖,李惠光.基于新双目模型的变结构视觉伺服控制方法[J].武汉理工大学学报,2009,31(10):117-120.
[2]马灿,毛建旭,邵思敏.基于视觉传感器的PCB缺陷检测系统的研究与实现[J].电子技术应用,2012,38(6):129-131.
[3]HUTCHINSON S,HAGER G D,CORKE P I.A tutorial on visual servo control[J].IEEE Trans.Robot.Automat.,1996,12(10):651-670.
[4]Wang Yuzhen,Feng Gang,Cheng Daizhan.Simultaneous stabilization of a set of nonlinear port-controlled Hamiltonian systems[J].Automatica,2007(43):403-415.
[5]Wang Yuzhen,Ge Shuzhi.Augmented Hamiltonian formulation and energy-based control design of uncertain mechanical systems[J].IEEE Transactions on Control Systems Technology,2008,16(2):202-213.
[6]Li Huiguang,Jin Mei,Zou Liying.A new binocular stereo visual servoing model[C].In:Proceedings of 2008 Pacific-Asia Workshop on Computational Intelligence and Industrial Application,PACIIA.WuHan,China:IEEE,2008:461-465.
[7]武波,李惠光.基于图像的直接视觉伺服控制器设计与仿真[J].系统仿真学报,2007,19(22):5214-5218.
[8]金梅,李惠光,邹丽颖,等.具有 L2性能的视觉伺服控制器设计[J].系统仿真学报,2009,21(13):4101-4105.
[9]梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2004.

