基于多步迭代算法的数字预失真技术

罗旭梅，何松柏，和 谦（电子科技大学 电子工程学院，四川 成都611731）

0 引言

在现代通信系统中，由于频带资源越来越紧张，频谱的利用率越来越受到重视。为解决该问题，多种高频谱利用率的传输技术和调制方式被相继提出，但是这类技术所传输的信号通常具有较高的峰均比和较宽的频带[1]。因功率放大器本身存在非线性特性，宽带信号经其放大后会产生失真，所以现代通信系统中对功放的线性度有了更高的要求。

目前，提高功率放大器线性度的主要方法有前馈线性化技术、负反馈技术、包络消除和恢复技术、LINC技术及数字预失真技术等。其中数字预失真技术因不存在稳定性问题且适用的带宽较宽、精度高、成本低等特点受到了广泛的关注。

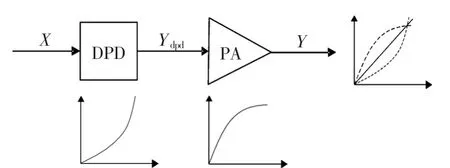
图1 数字预失真的基本原理

数字预失真的基本原理如图1所示，即在功率放大器的前端级联一个特性与之相反的数字预失真器DPD，从而使整个系统呈线性效果。

数字预失真的基本原理也可以理解为：在数字预失真技术中，首先对待优化功率放大器（PA）建立行为模型，然后通过模型求逆[2]的方法得到对应数字预失真器（DPD）。将该数字预失真器级联到功放的前端，如图1所示，则可达到提高该功率放大器线性度的目的。

为使上述所求数字预失真器能够更好地补偿功放的非线性，且保证功率放大器的工作效率，一种新型迭代算法被提出。

1 记忆多项式模型（MP）

记忆多项式模型是目前较为流行的一种模型，其在对有记忆效应的功放进行预失真处理时有很好的性能，且模型的复杂度较低，便于实现。所以本文基于该模型对功率放大器进行数字预失真处理。

记忆多项式的数学表达式通常为：

其中，amk为模型的系数，K为模型的阶次数，M为模型的记忆深度。由于多项式中的阶次数K、记忆深度M影响着模型的精确度，所以选取合适的模型阶次数及记忆深度也很重要。实际应用通过比较不同K、M情况下模型输出与实际输出的归一化均方误差（NMSE）来确定最佳的模型阶次数及记忆深度值[3]，如此确定了功放最终行为模型的数学表达式。

记忆多项式表达式（1）可以等价为：

在基于记忆多项式模型的数字预失真方法中，无论是功率放大器的模型还是预失真器的模型，均可等价为存在M个查找表，且每个查找表的深度为建模信号的点数。由式（2）可看出，该查找表的具体内容与输入信号的幅度直接相关。所以研究功放输入信号的时域特性是十分有意义的，下面将通过MATLAB对功放输入信号的时域特性进行分析。

2 功放输入信号的时域特征

由功率放大器的AM-AM特性曲线知，功放的非线性失真表现为对输入信号的峰值压缩。为使整个放大系统输出呈线性，所以希望功放的输入信号的峰值预先有相应扩张的特性，即功放输入信号较原信号有较高的峰均比（PAPR）。图2为原信号及预失真信号的时域波形。

图2 信号的时域特性波形

由图2可见，预失真信号在幅值较大的区域内有信号扩张的特性。即在数字预失真技术中，通过对功放模型求逆方法得到的数字预失真器DPD对信号峰值有扩张作用[4]，该预失真器初步实现了对功放非线性的补偿。

通过MATLAB求解得各信号的峰均比(PAPR)如表1所示。

表1 各信号的PAPR

由表1可看出，信号经过功率放大器后，其PAPR降低，而经过预失真器后PAPR反而提高。如此，当输入信号经过DPD后，信号失真表现为峰值扩张，其PAPR增加；而当该信号经过功放时，其非线性失真表现为对信号的压缩，即PAPR有所降低。最终信号在经过整个系统后其PAPR值保持基本一致，从而使整个放大系统的线性度得到改善。

由于预失真信号的峰均比（PAPR）较原信号有所提高，所以与原信号相比，预失真信号在经过功放时会受到更大的压缩。为补偿该额外的失真部分，本文提出多步迭代求取预失真器的方法。

3 多步迭代算法

为了使所得数字预失真器能更好地补偿待优化功放的非线性，本文提出多步迭代求取预失真器的方法。

多步迭代算法求取数字预失真器的结构框图如图3所示。

图3 迭代算法获取数字预失真器

以信号X作为功放的原输入信号，实验通过频谱仪采集功放的输出信号 Y，如图 3所示，然后将输入/输出两组信号进行归一化并对齐处理。利用处理后的输入/输出数据求解该功放模型PA1，通过对功放模型求逆的方法得到相应的数字预失真器DPD1。将该数字预失真器级联到功放的前端则可初步实现提高功率放大器线性度的效果。

进行一次迭代时，将原信号X通过上述所求预失真器DPD1后得到的预失真信号Ydpd1进行保存；以该预失真信号作为功放的新的输入信号，利用频谱仪重新采集功放此时的输出信号Y1；对信号Ydpd1、Y1进行归一化对齐处理，利用处理后的数据求解功率放大器的模型PA2；通过对功放模型PA2求逆，得到新的数字预失真器DPD2。

由此类推，可进行多次迭代来求取更优的数字预失真器，直至预失真效果再无明显改善为止。

由上节理论分析知，数字预失真器对于信号的峰值具有扩张作用，所以在迭代求取预失真器的过程中，预失真信号的峰均比会越来越高。然而，高峰均比的信号在通过功放时，使功放的工作状态过早进入接近饱和的区域，导致功放的工作效率下降。且当峰均比过高的信号做功率放大器的输入时，该高峰均比信号会使功放晶体管过热，从而使其功放对信号压缩得更严重，不但导致数字预失真器失效，而且可能毁坏整个放大系统。所以，为防止这种现象发生，限制预失真信号的PAPR是十分有必要的。

所以在新型迭代算法中，使用频域削峰技术处理信号，使功放的工作区域控制在1 dB压缩点附近[5]。削峰技术与预失真技术的结合使用既保证了功放的效率，又很好地提高了其线性度。

4 实验结果

实验选取带宽为5 MHz的单载波WCDMA信号为原信号，连续F类功率放大器为测试对象。通过基于有记忆多项式模型的数字预失真方法对该功放进行线性优化处理。通过比较功放输出信号的邻信道功率比（ACPR）来比较功率放大器线性度的改善程度[6]。

当原WCDMA信号作为功放输入时，功放的输出频谱图如图4所示，可知此时功放输出信号的ACPR为-40.59 dB。

图4 功率放大器的输出信号

不进行迭代时，即以原WCDMA信号作为功放的输入信号，采集功放的输出信号，基于记忆多项式模型对功放进行建模，通过模型求逆得到相应的数字预失真器DPD1。以该数字预失真器对功放进行线性优化，其预失真效果如图5所示。

图5 未迭代的预失真效果

由图5可以看出，经过预失真后的功放输出信号ACPR已降到-49.19 dB，相对于没有优化的功放输出ACPR改善了约8.6 dB。

下面将削峰技术和多次迭代求取预失真器的方法结合使用，两次迭代得到新的预失真器记为DPD3。将该数字预失真器级联到功率放大器的前端，通过实验得到预失真器DPD3对功放的线性化效果如图6所示。

由图6可以看出，经过优化后的预失真器对功放的线性度有了更好的改善。功放输出信号的ACPR值如表2所示。

由表2实验数据可清晰地看出，直接利用对功放模型求逆得到的数字预失真器对功放进行预失真处理时，使功放输出信号的ACPR改善了8.6 dB；而结合削峰技术和迭代方法求得的数字预失真器在对功放进行线性化处理时，使得功放的输出ACPR改善20.66 dB，比前者有明显的优势。

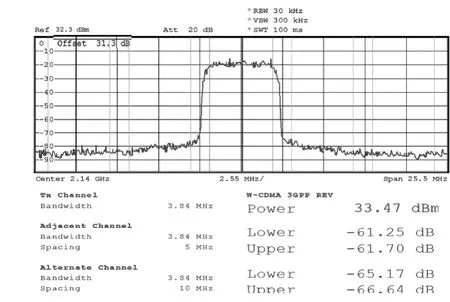
图6 优化预失真器后功放的输出

表2 功放输出信号的ACPR

5 结论

本文提出了利用迭代求取数字预失真器的方法来获得更优的数字预失真器。通过分析信号的数学特性，指出限制功放输入信号峰均比的重要性，从而在预失真过程中引入了频域削峰技术。文章的实验采用基于记忆多项式模型的方法对实际连续F类功放做数字预失真处理。实验结果显示，结合削峰技术与迭代求取预失真的方法对功放进行线性化处理时效果最优，该新型迭代算法可使系统输出信号的ACPR改善20.66 dB。

[1]Ding Lei，ZHOU G T，MORGAN D R，et al.Memory polynomial predistorter based on the indirect learning architecture[C].Global Telecommunications Conference，2002，GLOBECOM′02，IEEE，2002，1：967-971.

[2]Ma Yuelin，He Songbai，AKAIWA Y，et al.An open-loop digital predistorter based on memory polynomial inverses for linearization of RF power amplifier[J].International Journal of RF and Microwave Computer-Aided Engineering，2011，21(5)：589-595.

[3]Ding Lei，Ma Zhengxiang，MORGAN D R，et al.A leastsquares/Newton method for digital predistortion of wideband signals[J].Communications，IEEE Transactions on，2006，54(5)：833-840.

[4]KIM J，KONSTANTINOU K.Digital predistortion of wideband signals based on power amplifier model with memory[J].Electronics Letters，2001，37(23)：1417-1418.

[5]NADER C，LANDIN P N，MOER W V，et al.Peak-toaverage power ratio reduction versus digital pre-distortion in OFDM based systems[C].Microwave Symposium Digest(MTT)，2011 IEEE MTT-S International，IEEE，2011：1-4.

[6]Ma Yuelin，YAMAO Y，AKAIWA Y.An algorithm for obtaining the inverse for a given polynomial in baseband[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2013，96(3)：675-683.