舰船舱室中电缆串扰分析

秦萌涛，宋文武，王冬冬

(电磁兼容性国防科技重点实验室，湖北 武汉 430064)

现代舰船包含大量的电气电子系统和设备，它们通过各种不同类型的传输、控制电缆实现互连和通信。通常将电缆捆成一束束的，这样既整齐美观，又便于固定，而且还便于维护检查和损坏时的维修。但由于电缆敷设密集，电缆之间的耦合串扰带来的电磁兼容性问题会严重影响系统和设备性能。如果系统出现电磁兼容性问题，则90%的可能性是由电缆或互连线之间的串扰引起的[1]。因此，预测分析舱室环境下电缆之间的串扰有重要的意义，也是迫切的课题。

对于电缆串扰的估算，通常有两种模型：

(1)低频时，可认为容性(电场)耦合和感性(磁场)耦合的参数大小仅与干扰电缆和被干扰电缆之间的等效电路形式有关而与频率无关，此时可采用集总参数模型[1]，该模型用电报方程来描述。如果电缆的阻抗矩阵以及相互耦合参数矩阵已知，可以根据等效电路得到串扰值的精确解，这对理解串扰作用的机制以及数值仿真验证都有帮助。

(2)对于更高的频率，可建立基于多导体传输线理论电缆串扰模型[2-3]。对于一个N根电缆的系统，其相互间的串扰决定于分布参数的N×N的阻抗矩阵和导纳矩阵、工作频率、相互位置以及终端阻抗的大小。

本文分别建立了共地的基于多导体传输线理论的电力电缆对屏蔽同轴线(SCC)，非屏蔽双绞线(UTP)和屏蔽双绞线(STP)的电缆耦合模型，在此基础上在CST-CS中建立其等效电路模型，并仿真分析了对应的串扰值。考虑到实际舱室电缆总是多根相邻成束，因此还仿真分析了多根电力电缆对多根传输或控制电缆的耦合干扰情况。

1 串扰的耦合机制

当两根或多根电缆相互邻近时，它们之间存在分布的互电容和互电感，这是电缆之间耦合的“源”。根据耦合的途径可将串扰分为容性耦合与感性耦合。

考虑最简单的三导体传输线模型，如图1所示。

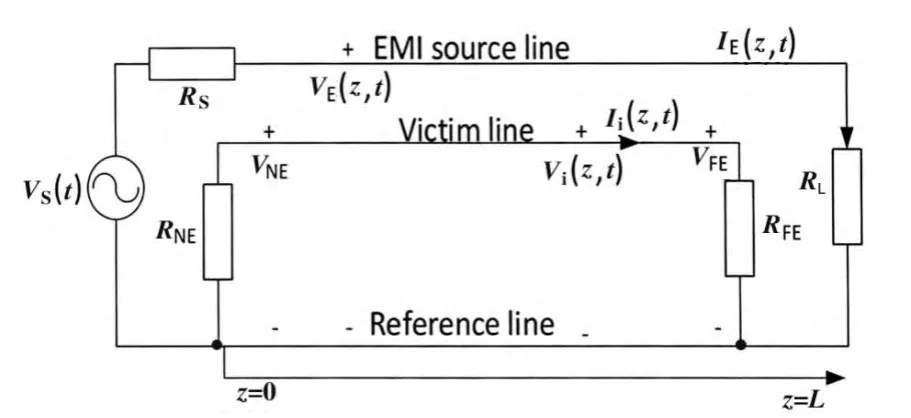
图1 三导体传输线的典型串扰模型

其中,Vs表示干扰电缆的驱动源，Rs是其驱动源，RL是终端阻抗。被干扰电缆的近端负载为RNE，远端负载为RFE。Ii(z,t)和Vi(z,t)分别表示被干扰电缆的感应电流和电压。VNE和VFE分别表示被干扰电缆近端和远端的电压值。

图1所示的模型的单位长等效电路如图2所示。

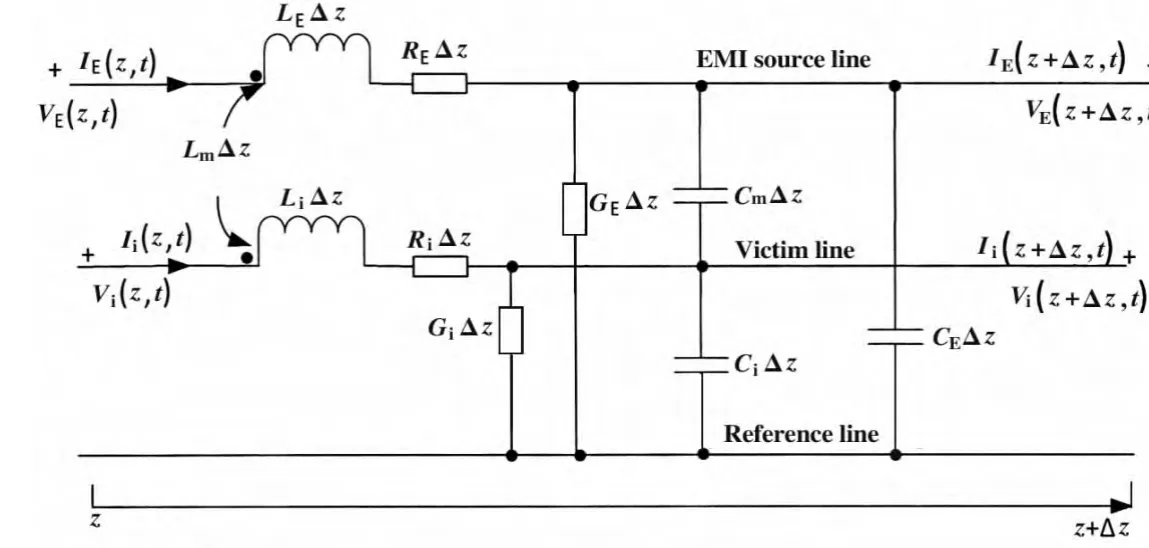
图2 三导体传输线模型单位长等效电路

根据电报方程，当Δz趋于零时，有：

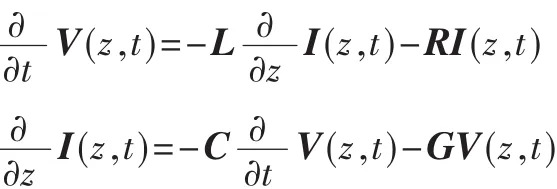
单位长分布参数矩阵为:

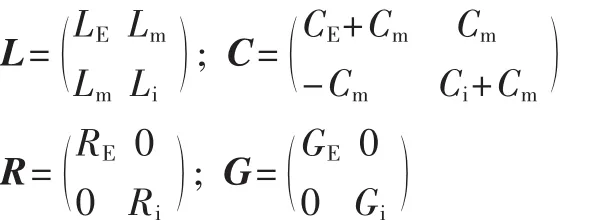
对于无耗传输线，弱耦合的情况，容易得到被干扰电缆近端和远端串扰值[4-5]。并且频率越高，电缆越长，串扰值越大。感性耦合在低阻抗负载时占主导地位，高阻抗负载时容性耦合则占主导地位。

在实际的模型中，相互之间的耦合参数Lm、Cm以及电缆到参考地的距离h、电缆之间间距d直接影响串扰值的大小。

从已有的一些公式和研究结果[6-9]可看出,互电感随着d的增加而减小，随着h的增加而增加，互电容随着d的增加而减小，而h对其无显著影响。

经过以上分析，很容易理解屏蔽层是如何保护电缆不受外界干扰的以及双绞线在减小串扰方面的优势。

(1)如果电缆带有屏蔽层，则屏蔽层能完全消除容性耦合，但只有两端均接地并且在某一截止频率之上能够一定程度地减小感性耦合。

(2)如果被干扰电缆是双绞线，一方面回路面积很小可减小感性耦合；另一方面双绞线的两根芯线的感应电流不仅方向相反，而且由于对称结构使得感应电流的大小也几乎相等。因此可最大限度地减小相互之间的耦合。

2 舱室环境下电缆串扰模型的建立

通常将最近的金属平面作为接地面，因此可将舱室壁作为参考地平面。这样，理论分析时可首先采用如下模型进行简化分析。

假设模型两根电缆的间距为d,距离参考地面的距离为h，其截面如图3所示。

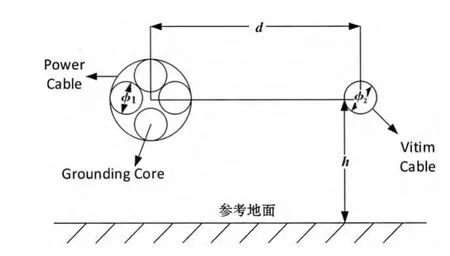
图3 串扰电缆的横截面示意图

该模型中电力电缆为四芯电缆，其中一根芯线为接地线，另外三根芯线分别由对称三相交流电来驱动，驱动电源均包含内阻,且各相终端都接相应的终端阻抗。

设电力电缆各相芯线两端的电压分别为：VA(0)、VA(L)、VB(0)，VB(L)和 VC(0)、VC(L)；被干扰电缆两端连接对应的终端阻抗为Zr(0)和Zr(L)。建立此模型的目的是为了估算该电缆两端的对地电压Vr(0)和Vr(L)以及流入参考地的电流值 Ir(0)和 Ir(L)，即串扰值。

根据多导体传输线理论和网络理论，可建立相应的链参方程为(假设电缆都是均匀的)：

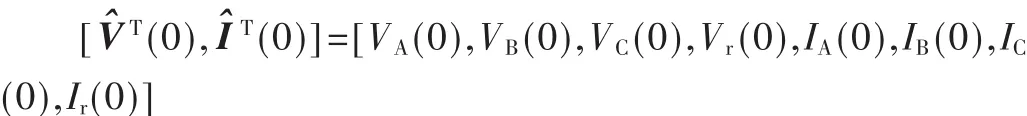
同理V(L)、I(L)为电力电缆各芯线和被干扰电缆远端电压、电流值组成的矩阵即：

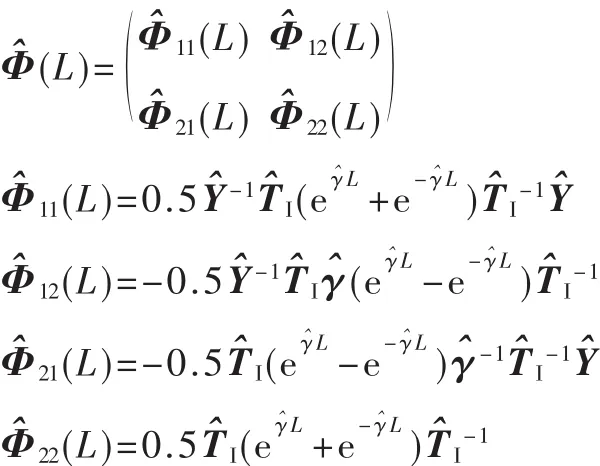
计算出整个线长的链参矩阵后，引入终端条件即可确定电缆的串扰值。而终端条件可根据Thevenin定理得到近端终端方程：

同理，远端终端方程为：

其中，V^P为驱动源组成的矩阵即:(0)和(L)为近端和远端终端阻抗矩阵。

联立式(1)、式(2)和式(3)可得到远端和近端的电缆串扰值。

在建立以上模型的基础上，可将舰船舱室中的电缆分为几段均匀传输电缆(单位长度分布参数不随位置变化而变化)，并分别对每段应用以上多导体传输线模型进行串扰的估算。

电缆沿舱室壁布置，分为三段，每段可认为是均匀传输线，在连接处可认为电压、电流值连续。采用多导体传输线理论分析时，整个电缆的链参矩阵可由三段的链参 矩 阵(L1),(L2)和(L3)表 示 为 方 程(4)：

得到整个电缆的链参矩阵后再应用如图2的电路配置建立近端和远端的终端方程进而计算被干扰电缆上耦合的串扰值。

对于多根电力电缆与多根被干扰传输电缆之间的串扰建模，其方法与以上介绍的相同，但模型复杂度尤其是电路配置的复杂度会增加很多，链式方程中各矩阵的阶数将会增加，因而计算复杂度也将加大。本文仅对2根电缆与3根被干扰电缆耦合情形进行了仿真。

3 CST-CS仿真实验结果

实际的电力电缆外有聚乙烯材料保护层,厚t1=5 mm；芯线内导体材料均为铜,驱动源各相芯线直径φ1=5 mm，接地线芯线直径为φ2=2.7 mm；芯线外层包有橡胶绝缘材料,厚 t2=1.1 mm；整个电力电缆的外直径为 φ3=26.4 mm。其横截面如图4所示。

电缆长度L1=L2=L3=1；两电缆间距d=50 mm,到舱室壁的距离h=50 mm；计算频率为 0～100 MHz。

(1)电力电缆为单根，仿真被干扰电缆为单根SCC、STP和UTP时的电缆串扰值。近端测试结果如图5所示。

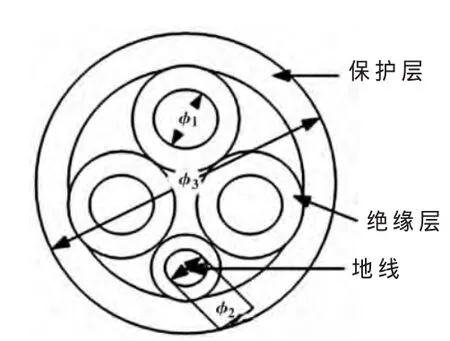
图4 电力电缆横截面示意图

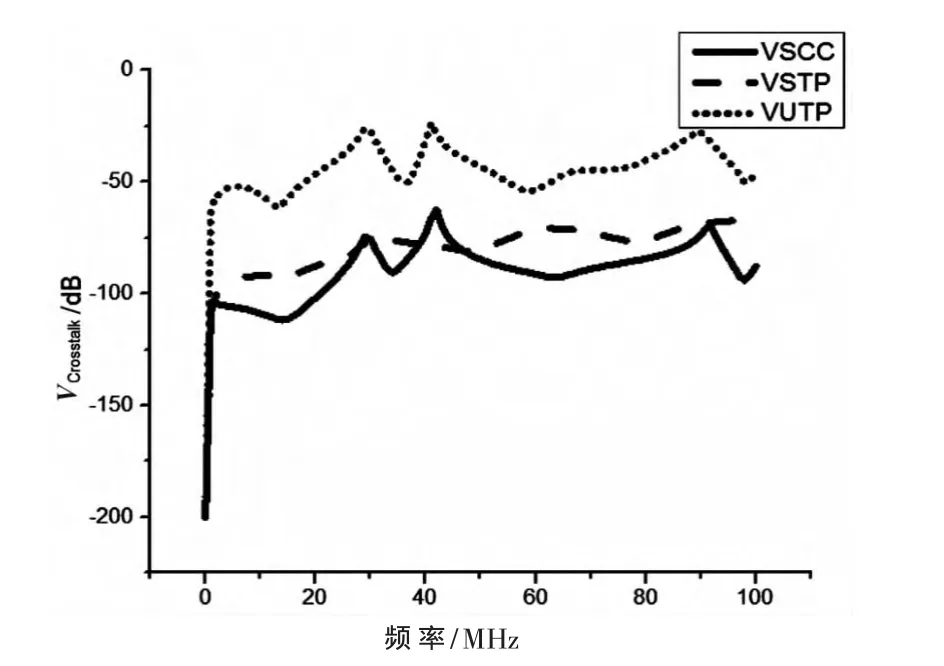
图5 三种被干扰电缆近端串扰电平

从图5可看出，屏蔽电缆比非屏蔽电缆的串扰值低大约50 dB。并且在计算工作频率为0～100 MHz范围内，非屏蔽双绞线和屏蔽同轴电缆均出现了几个谐振频率点，而屏蔽双绞线未出现，这是由模型中的不同传输线的分布参数矩阵决定的，说明非屏蔽双绞线和屏蔽同轴电缆易受到低端频率的干扰。

(2)电力电缆为 2根，被干扰电缆为 3根，分别仿真被干扰电缆为单根SCC、STP和UTP时的电缆串扰值。电缆的布置具体位置如图6所示。

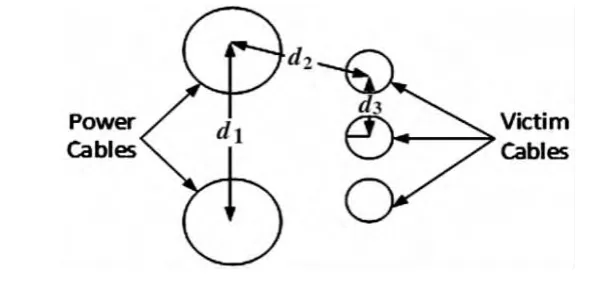
图6 多电缆布置的相对位置

电缆的相对位置参数：d1=29 mm,d2=49.8 mm,d3=8 mm。

当被干扰电缆为屏蔽同轴电缆(SCC)时，3根SCC近端的串扰电平值如图7所示。

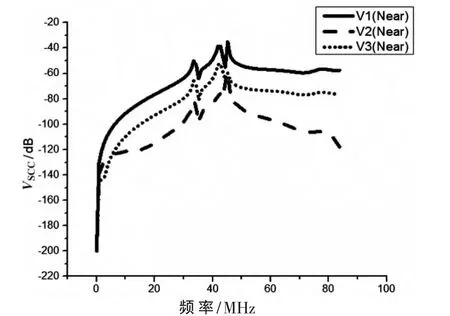
图7 3根被干扰SCC近端串扰电平

当被干扰电缆为STP时，3根STP近端的串扰电平值如图8所示。

图8 3根被干扰STP近端串扰电平

当被干扰电缆为UTP时，3根STP近端的串扰电平值如图9所示。

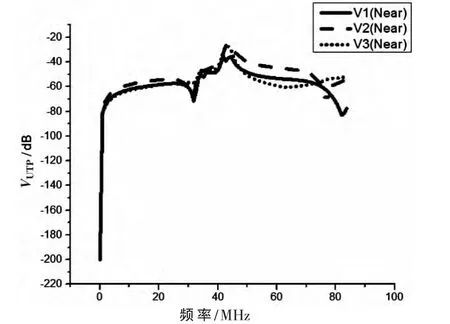
图9 3根被干扰UTP近端串扰电平

从图7、图8和图9可看出，多电缆串扰时，随着频率的增高，低频端的串扰值也随之增加。耦合谐振频率增加了许多，也说明多电缆相互串扰机制更加复杂。

依据电缆间的耦合机制和模型的仿真结果，可采取以下措施来抑制串扰：

(1)电缆束布置应尽量靠近舱室壁，这一方面可以增加电缆对地的电容，从而减小相互之间的容性耦合；另一方面可以减小回路面积，从而减小电缆之间的感性耦合。

(2)电缆之间应保持一定的间距，特别是强电输电线路应与弱电传输线分别捆成束。

(3)如果条件允许,可以在电缆束中增加一条参考地电缆,这样可减少信号或控制传输电缆之间的相互干扰。

本文依据多导体传输线理论建立了舰船舱室中电缆串扰的模型，并以此模型为基础在CST-CS中对各电缆进行了实际的电路配置，仿真了单根电力电缆与单根SCC、STP、UTP之间的串扰。结果表明屏蔽电缆比非屏蔽电缆的串扰值低大约50 dB，并且平衡传输屏蔽双绞线在频率低端不易受到干扰。此外，本文对多根电缆串扰的仿真表明，被干扰电缆耦合的谐振频率增多，耦合机制更加复杂。综上所述，本文的结果对舰船电缆的串扰分析以及实际布置有一定的指导作用。

[1]何红,等.电磁兼容和电磁干扰[M].北京：国防工业出版社,2007：44-45.

[2]PAUL C R.Introduction to electromagnetic compatibility[M].Hoboken,NJ:Wiley,2006.

[3]TESCHE F M,et al.EMC analysis methods and computational models[M].New York:Wiley,1997.

[4]Ruan Ligang,et al.Crosstalk analysis of aircraft wires[J].Shanghai:Civil Aircraft Design and Research,2010.

[5]PAUL C R,FEATHER A E.Computation of the transmission line inductance and capacitance matrices from the generalized capacitance matrix[J].IEEE Trans.Electromagn.Compat.EMC-21,1976.

[6]VANCE E F.Coupling to shielded cables[M].Edward F.Vance.New York:Wiley,1978.

[7]PAUL C R.Analysis of multiconductor transmission lines[M].Wiley-Interscience,New York,1994.

[8]PAUL C R．Computation of the transmission line inductance and capacitance matrices from the generalized capacitance matrix[J].IEEE Trans.on Electromagnetic Compati bility．1976，11，EMC-18(4):175-183．

[9]PAUL C R.MCKNIGHT J A:Prediction of crosstalk involving twisted pairs of wires,Part I:A transmission line model for twisted wire pairs[J].IEEE Trans.Electromagn.Compat.EMC-21,92–105(1979).