激光损伤1064nm增透熔石英的热应力数值模拟研究

蔡继兴，张烨，王頔，渠旭，李贺，金光勇

（长春理工大学 固体激光技术与应用吉林省重点实验室，长春 130022）

激光对熔石英及其表面膜层材料的损伤是一个复杂的物理过程，它主要由两方面的性质决定：一是激光参数，如激光脉宽、能量密度、重复频率、光斑半径等；二是材料的自身属性。不同的激光条件会对同一种材料产生不同的作用效果，相同激光条件下对不同的材料也会产生不同的损伤效果［1］。根据损伤效果的不同分为热损伤、应力应变损伤、致燃损伤、爆轰波损伤以及多种损伤效应的耦合作用等。它们都在很短的时间内产生相互影响，给研究工作带来极大的困难。1064nm增透熔石英是光学系统中常用的窗口材料，光路中任何窗口材料的损伤都会造成很大的损失，甚至造成整个系统不能稳定运行。因此，研究1064nm增透熔石英窗口的损伤，特别是对其损伤效果及损伤机理的研究具有重要的意义和应用价值［2］。

1 理论模型

1.1 几何模型

由于激光在空间中为高斯分布，所以计算时采用圆柱坐标系，假设熔石英及其表面膜层材料为各向同性的连续介质，激光辐照到材料表面后的能量吸收为体吸收［3］，则所建立的激光损伤1064nm增透熔石英的几何模型如图1所示，其中膜层厚度h=5.5×10-4mm，熔石英基底厚度d=4mm，材料半径a=11.25mm。

图1 几何模型

1.2 数学模型

1.2.1 热传导方程

由于采用的是毫秒脉冲激光，其与1064nm增透熔石英的能量交换过程主要体现为热交换，忽略材料与周围空间的辐射和对流过程，热传导方程可以表示为如下形式［4］：

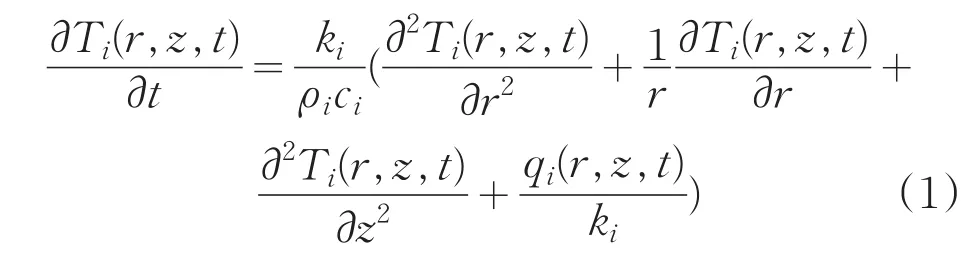
其中，Ti(r,z,t)为t时刻的温度分布，ki、ρi和ci分别代表材料的热传导系数、密度和比热，i=f、s分别代表膜层和熔石英基底，上述热传导方程的热源项可以表示为［5］：

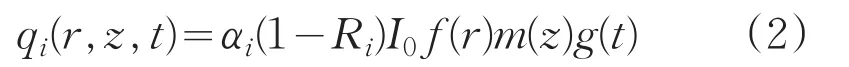
式中：

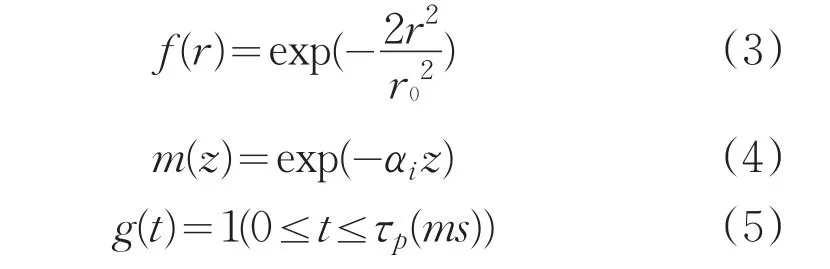
其中，f(r)和g(t)分别代表激光的空间和时间分布；r、z分别为柱坐标系的径向、轴向坐标，r0为激光光斑半径，αi为膜层和熔石英的吸收系数，τp为激光脉宽，Ri为膜层和熔石英的反射率，I0为激光的中心功率密度［6］。

1.2.2 弹性力学方程

在圆柱坐标系下，与上述热传导方程耦合的弹性力学方程可以表示为如下形式［7，8］：

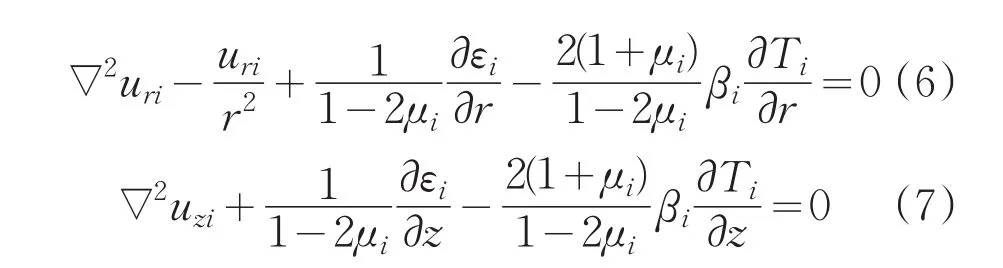
其中，uri和uzi分别代表位移在r和z方向上的分量；μi、εi和βi分别为材料的泊松比、体应变和热应力系数。

2 数值模拟结果和分析

图2所示为在能量密度3.1831×103J/cm2，脉宽1ms，光斑半径1mm的单脉冲激光作用下，1064nm增透熔石英上表面温度随径向位置和时间的变化关系。由于激光束为高斯对称分布，根据1064nm增透熔石英的熔点特性，可知1064nm增透熔石英在t=0.96ms时熔融区的半径r=0.2mm，从而计算出激光作用后1064nm增透熔石英熔融热损伤面积约为0.126mm2。

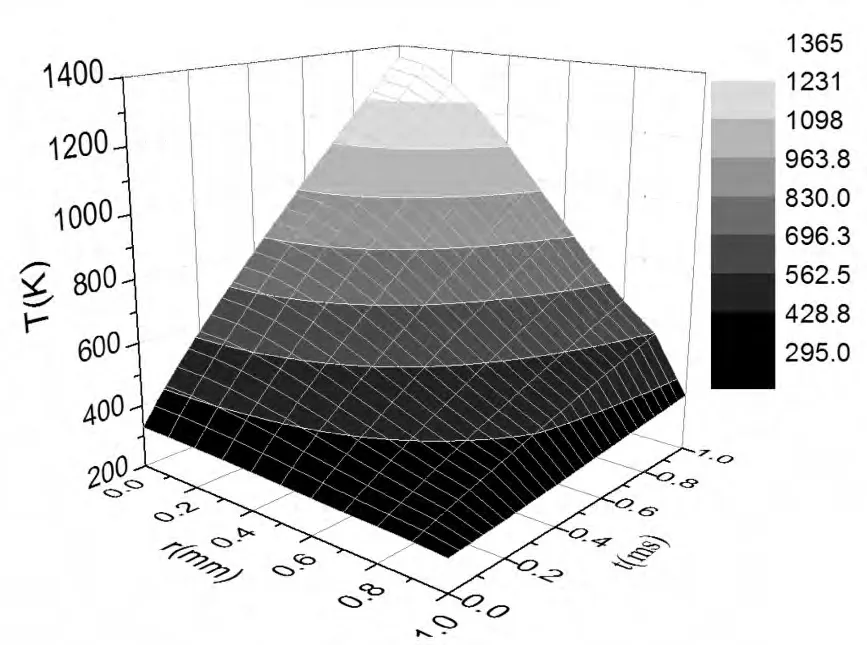
图2 上表面温度随径向位置和时间的变化

对应特征径向位置和特征时刻作二维投影，给出上述激光参数条件下1064nm增透熔石英上表面特征径向位置处，温度随时间的变化关系，如图3所示；特征时刻1064nm增透熔石英上表面温度随径向位置的变化关系如图4所示。

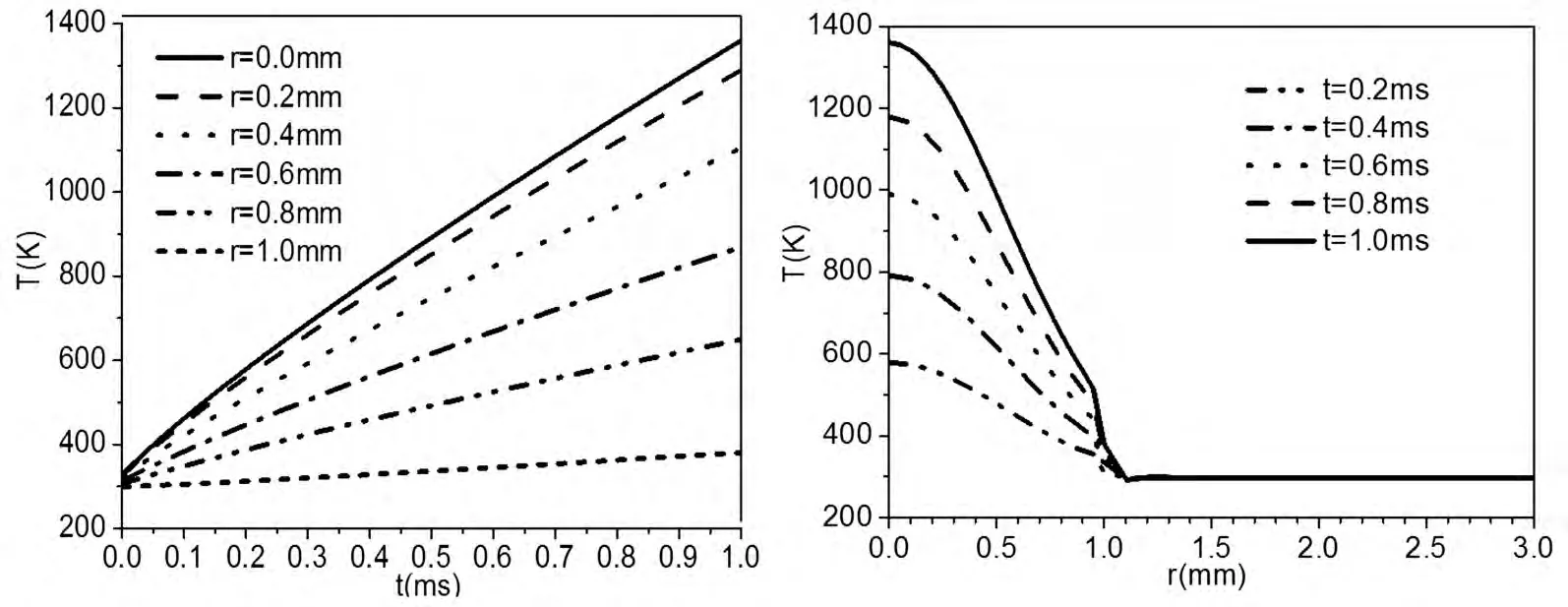
图3 上表面特征径向位置温度随时间的变化

从图3可知，在激光光斑半径区域内，随激光作用时间的增加，1064nm增透熔石英上表面各点温度值均逐渐增加。在激光辐照中心点产生的温升最大值约为1360K，超过了膜层材料的熔点值；在光斑半径边缘产生的温升值最小，约为380K，沿材料半径方向各点的温升呈下降趋势。

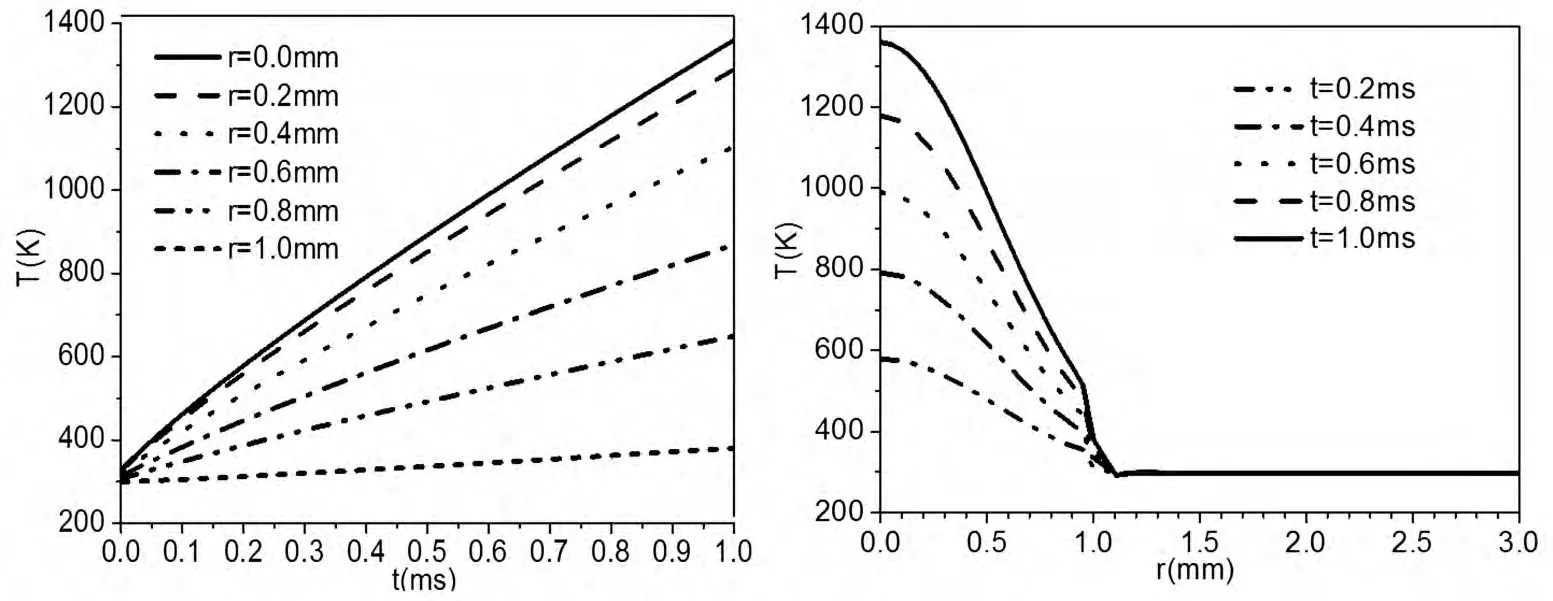
图4 上表面特征时刻温度随径向位置的变化

由图4可知，激光辐照时间越长，温升越高，材料表面产生的温度梯度也越大。在激光辐照区域内，温升较集中，在激光光斑边缘附近，形成较大的温度梯度。当激光作用结束时，形成的温度梯度达到最大，据此可知在材料内部将产生较大的热应力。因此，判断1064nm增透熔石英是否发生损伤，主要依据激光作用结束时，材料内部产生的热应力是否超过了膜层及熔石英的抗拉强度或抗压强度。

图5 不同能量密度条件下上表面投影中心点温度随脉冲宽度的变化

图5所示为能量密度分别取2.5465×103J/cm2、2.8648×103J/cm2和 3.1831×103J/cm2激光条件下，1064nm增透熔石英上表面中心点温度随激光脉冲宽度的变化关系。当脉冲宽度一定时激光能量密度越高，材料表面温度越高，由于材料表面中心点的温度高低主要由该点的激光辐照能量密度大小决定，因此在激光光斑半径相同的条件下，激光脉宽越大，激光能量密度值就越小，作用到材料表面后产生的温度逐渐降低。

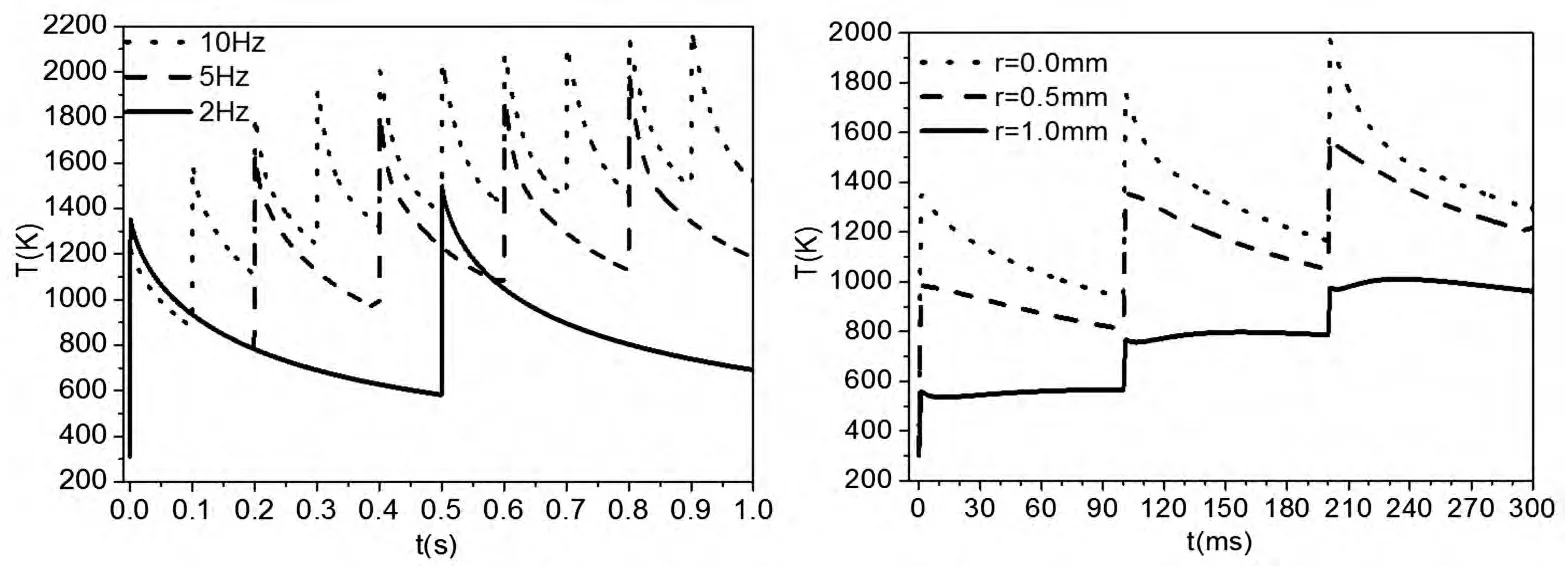
图6 上表面投影中心点温度随时间的变化

图6所示为激光重复频率分别为2Hz、5Hz和10Hz条件下，1064nm增透熔石英上表面投影中心点温度随时间的变化关系。在激光辐照期间，中心点的温度急剧上升，在脉冲停止作用的脉冲间隔内，由于没有能量的聚集，材料处于冷却阶段，表现为激光作用中心点温度的降低，温升曲线呈锯齿状。

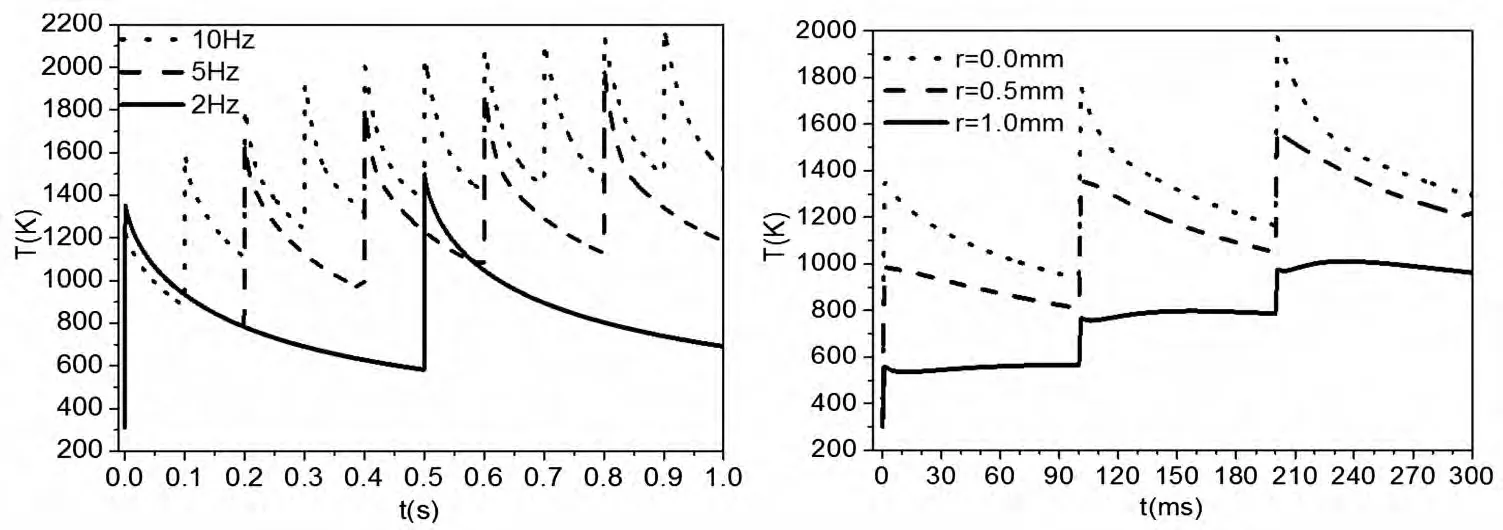
图7 上表面特征径向位置温度随时间的变化

图7所示为相同激光参数条件下，1064nm增透熔石英上表面特征径向位置温度随时间的变化关系，当第二个脉冲作用于材料表面后，材料上表面中心点的温升值约为1763K，第三个脉冲作用于材料表面后，材料上表面中心点的温升值已经达到1972K，两者均超过了膜层及熔石英基底的熔点值。因此可以判定，当脉冲串激光作用于1064nm增透熔石英表面后，将会产生一定的温度累积效应，其效果使材料的损伤程度加剧。

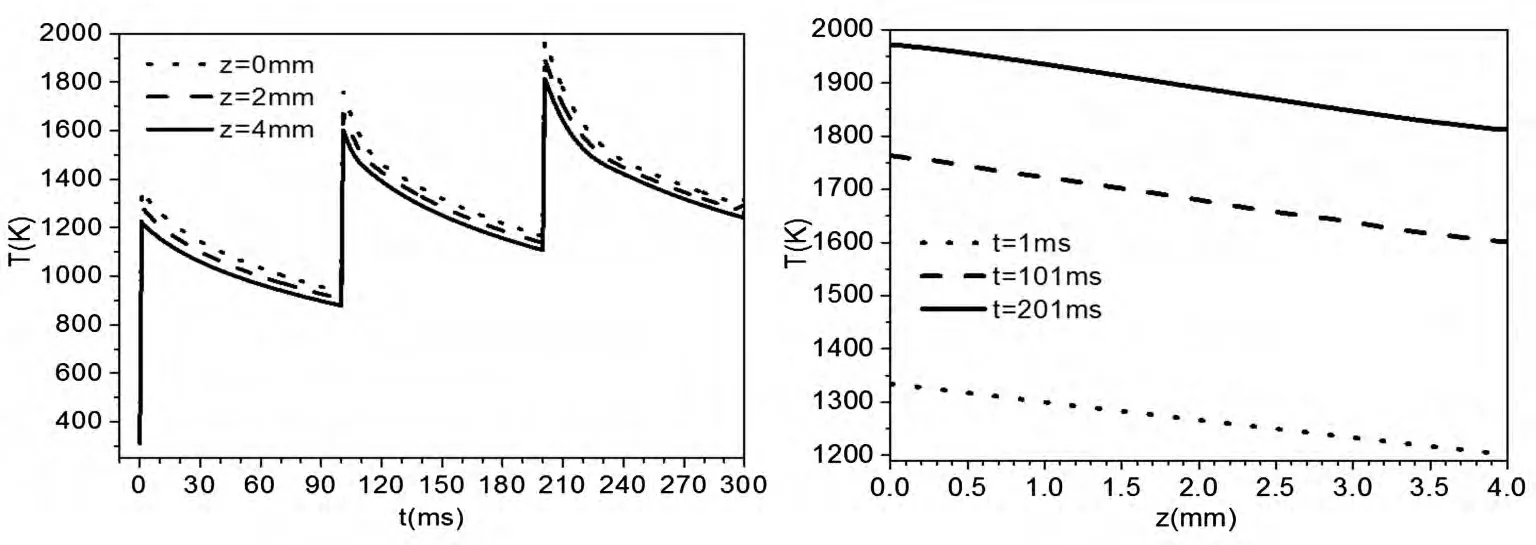
图8 特征轴向位置温度随时间的变化

图8所示为相同参数的脉冲串激光作用下1064nm增透熔石英特征轴向位置温度随时间的变化关系，1064nm增透熔石英上表面的温升最大值要高于后表面的温升最大值，且随脉冲个数的增加，轴向不同位置处的温升最大值依次升高，即在轴线方向上存在一定的温度累积效应。

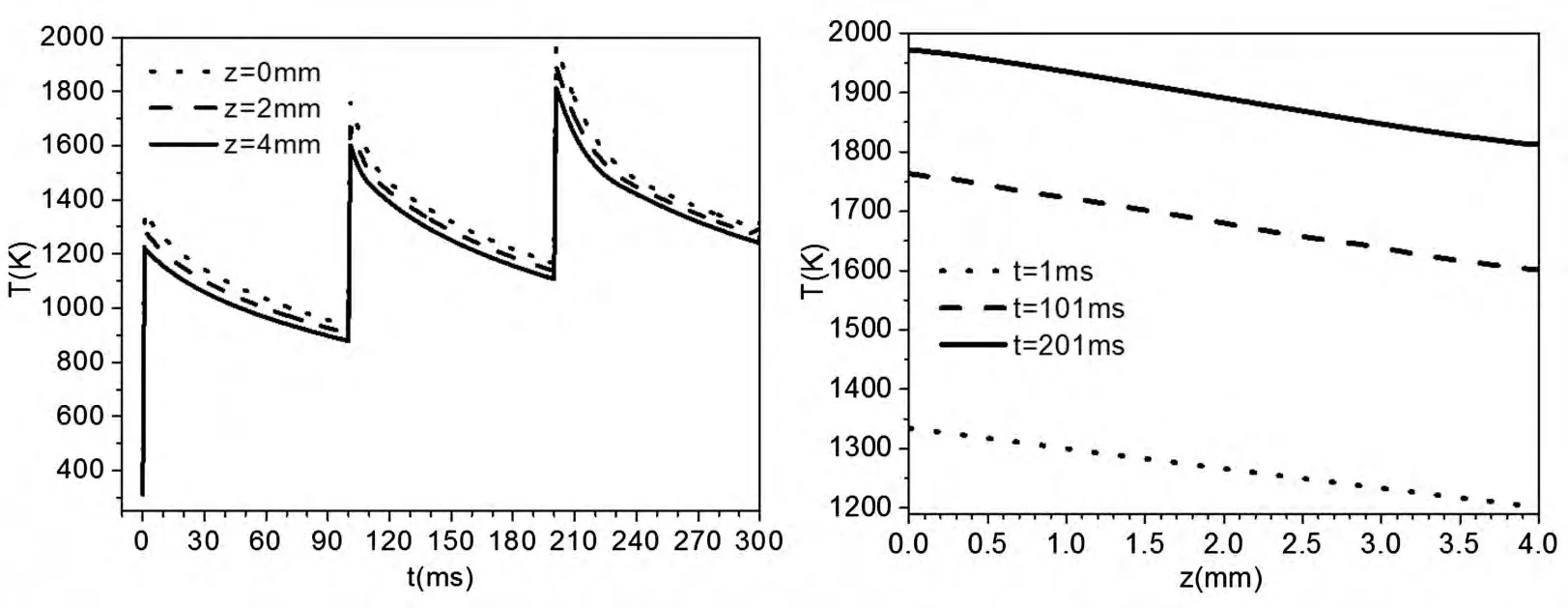
图9 特征时刻温度随轴向位置的变化

图9所示为前三个脉冲激光作用结束后1064nm增透熔石英温度随轴向位置的变化关系，可以看到随激光脉冲个数的增加，轴向各点的温度均上升。1064nm增透熔石英在t=101ms、201ms时，其热熔融区的深度已经由z=3.2mm增加至z=4.0mm，热熔融区已经由上表面至下表面贯穿整个材料。

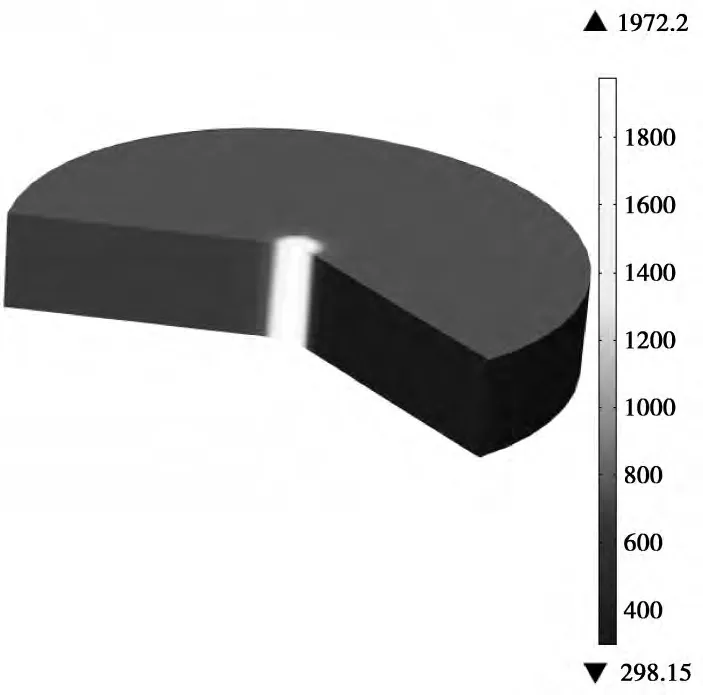
图10 1064nm增透熔石英温度分布

图10所示为脉冲串激光作用结束后1064nm增透熔石英温度的三维分布图，当最后一个脉冲作用结束后，其热熔融区域半径约为0.7mm（单脉冲作用时的热熔融半径约为0.2mm）。可见，相比于单脉冲激光，脉冲串激光将会产生一定的温度累积效应，其效果是使得材料的损伤面积和损伤深度增加。由于激光脉冲为高斯分布，根据1064nm增透熔石英的熔点、气化点等特性，可以得到激光脉宽为1ms，能量密度为3.1831×103J/cm2，重复频率为10Hz条件下，3个脉冲作用截止时，其热熔融损伤体积约为6.158mm3。

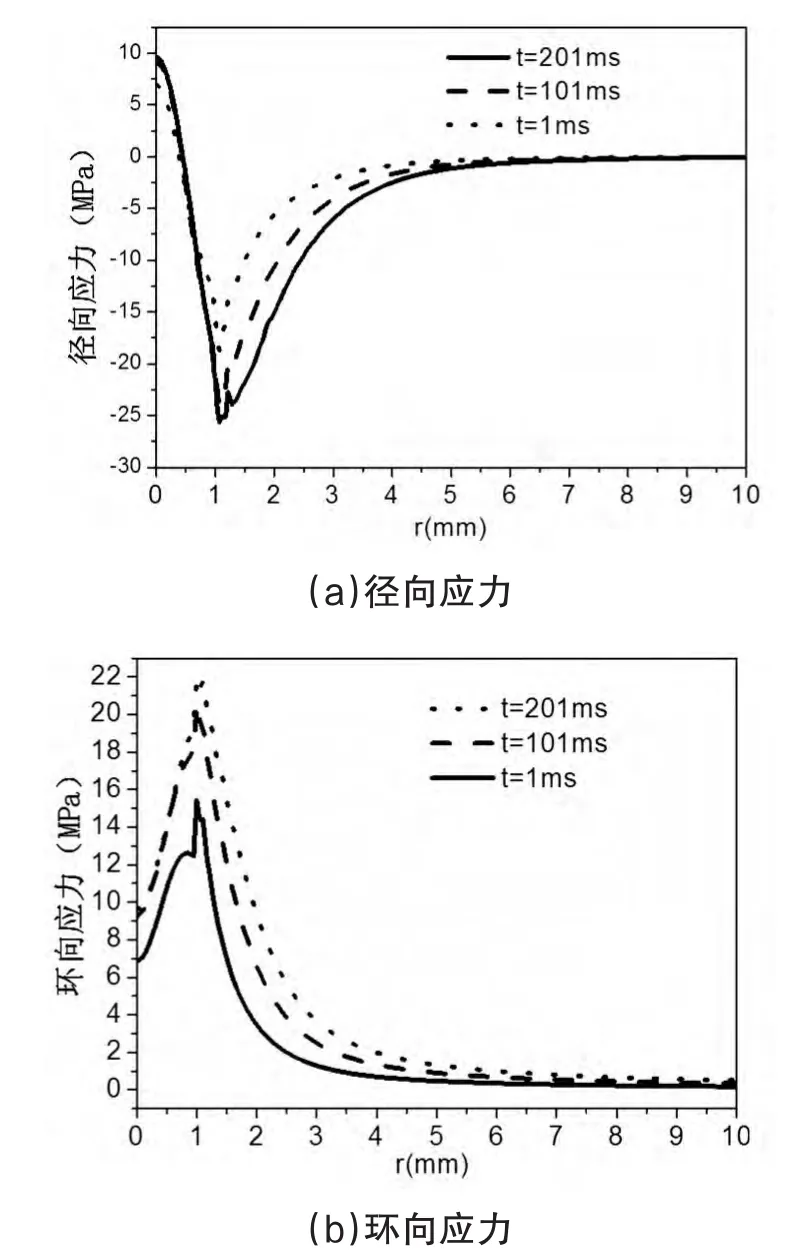
图11 上表面径向/环向应力随径向位置的变化

图11所示为特征时刻1064nm增透熔石英上表面径向应力、环向应力随径向位置的变化关系，在上表面中心处，径向应力表现为拉应力，且拉应力达到最大值，随脉冲个数的增加，拉应力逐渐增加；在半径方向上，拉应力逐渐减小，并逐渐转化为压应力。同时发现，在激光光斑半径边缘附近压应力达到了最大值。据此可以判断，1064nm增透熔石英发生损伤时，应首先从激光作用中心点或激光光斑半径边缘附近开始。从图11（b）可以看到，1064nm增透熔石英上表面环向应力始终体现为拉应力，且随脉冲个数的增加，拉应力逐渐增大。在半径方向上，拉应力先逐渐增加，并在光斑半径边缘附近达到最大，然后逐渐减小并最终趋向于零。根据1064nm增透熔石英的应力特性，可以得到1064nm增透熔石英在t=201ms时超过应力屈服强度区域对应的径向半径r=1.5mm，从而计算出激光作用后1064nm增透熔石英应力损伤面积约为7.069mm2。

图12所示为1064nm增透熔石英径向应力、轴向应力随轴向位置的变化关系，在材料表面中心处，径向应力表现为拉应力，且随脉冲个数的增加，拉应力逐渐增大。沿轴线方向，拉应力逐渐减小并逐渐转化为压应力，压应力在轴向上先逐渐增大，并在z=1mm附近处达到最大值，然后趋缓逐渐降低，并在距离后表面0.5mm附近处迅速减小并逐渐转化为拉应力，拉应力在1064nm增透熔石英后表面中心位置达到最大值。

在轴线方向上，轴向应力始终表现为压应力，且随脉冲个数的增加压应力逐渐增大。轴向应力沿轴向位置先逐渐增大并在轴向中心位置处达到最大值，然后逐渐减小，并在后表面中心位置处减小为零。根据1064nm增透熔石英的应力特性，可以得到1064nm增透熔石英在t=201ms时超过应力屈服强度区域对应的轴向深度z=4mm。

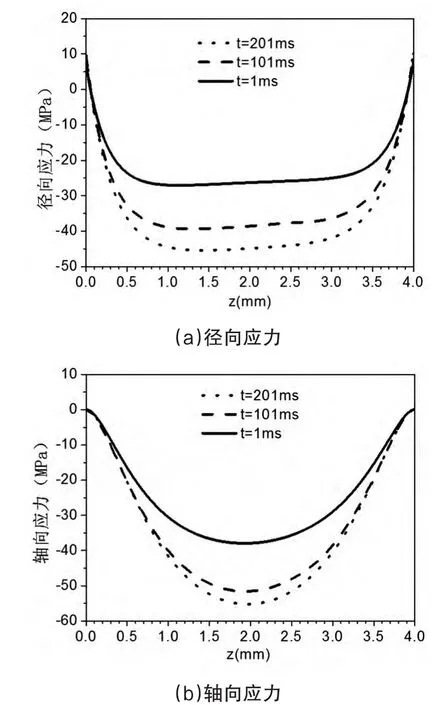
图12 径向/轴向应力随轴向位置的变化关系

3 结论

本文根据热传导方程和弹性力学方程，在假设熔石英及其表面膜层材料为各向同性的连续介质条件下，建立了激光损伤1064nm增透熔石英随时间变化的温度场和应力场的理论模型。采用数值模拟方法，计算并分析了单脉冲及脉冲串条件下，激光能量密度、脉冲宽度和重复频率的变化对1064nm增透熔石英温度和应力的影响，并分别对其损伤效果和损伤机理进行了探讨。论文研究结果可为激光损伤1064nm增透熔石英的理论和数值模拟研究提供依据，同时也为长脉冲激光对熔石英材料的损伤机理分析奠定了基础。

［1］付耀龙，孙振皓，徐立君.长脉冲激光辐照硅材料热应力的数值模拟［J］.长春理工大学学报：自然科学版，2013，36（3-4）：107-109.

［2］Dai G，Chen Y B，Shen Z H，et al.Analysis of laser induced thermal mechanical relationship of HfO2/SiO2high reflective optical thin film at 1064nm［J］.Chinese Optics Letters，2009，7（7）：601-604.

［3］Yoshida K，Umemura N.Influence of beam spatial distribution on the laser damage of optical material［J］.J Appl Phys，2006，49（8）：3815-3819.

［4］孙承伟.激光辐照效应［M］.北京：国防工业出版社，2002：310-314.

［5］胡汉平.热传导理论［M］.合肥：中国科学技术大学出版社，2010.

［6］戴罡，陆建，刘剑，等.长脉冲激光致两种典型光学薄膜损伤阈值的测试与分析［J］.测试技术学报，2011，25（2）：122-127.

［7］宋林森，史国权，李占国.ANSYS在激光打孔温度场仿真中的应用［J］.长春理工大学学报：自然科学版，2006，29（4）：19-21.

［8］徐秉业.简明弹塑性力学［M］.北京：高等教育出版社，2011：18-23.