基于亮点迹线跟踪的逆合成孔径成像运动补偿技术

何心怡，邓建辉，蒋 飚

(1.海军装备研究院，北京100161;2.杭州应用声学研究所，浙江 杭州310012)

0 引 言

水中目标的声学成像技术起源于雷达成像，而成像雷达主要有2 种:合成孔径雷达 (Synthetic Aperture Radar，SAR)和逆合成孔径雷达(Inverse Synthetic Aperture Radar，ISAR)，其中SAR 以其高分辨率、全天候、穿透性强等优点被公认为是现代微波遥感领域一项突破性的成就，并被广泛应用到军事和民用等方面;ISAR 是在SAR的基础上发展起来的又一种高分辨成像雷达［1－5］。如果让雷达不动，而目标运动，从获取回波的多普勒信息的观点来看，二者等价，ISAR 就是采取后一种工作方式。国际上从20世纪60年代开始发展ISAR，目前已得到广泛应用［6－9］。

与雷达成像类似，声呐中对应的也有合成孔径声呐(Synthetic Aperture Sonar，SAS)和逆合成孔径声呐(Inverse Synthetic Aperture Sonar，ISAS)，并且至今已有30 多年的发展历史［10］。目前SAS 已在海洋测绘等领域得到广泛应用，而ISAS 是在SAS 技术上逐步发展而来的，虽然它们的原理相似，然而ISAS的技术难度要大许多，主要因为ISAS 针对的是非合作运动目标，很难得到目标运动的精确信息，而往往需要从目标回波中获取，这给运动补偿带来了相当的难度;其次，也很难得到目标本身在此期间成像姿态的变化信息，这些都会导致成像质量的下降。为此，ISAS 必须对目标运动的非线性成分进行估计和补偿，才能获得满足使用要求的成像效果。因此，运动补偿是近年来逆合成孔径声呐的研究重点，如文献［11］研究了旋转运动目标的距离－多普勒逆合成孔径成像方法。

文中针对水下目标逆合成孔径成像的运动补偿问题，研究提出了一种基于回波亮点迹线跟踪的目标漂移运动补偿技术，并通过仿真试验验证其正确性、有效性和可行性，并具有良好的实用前景。

1 ISAS 原理

1.1 信号模型

图1为ISAS 成像的几何示意图，T/R 分别为声呐的接收/发射基阵(即声呐基阵)。声呐基阵坐标系为(U，V，W)，目标坐标系为(x，y，z)。为了表示目标旋转，引入参考坐标系(u，v，w)。考虑声呐和目标在同一平面上，设t = 0 时刻x 轴与u 轴重合，则在t 时刻发射基阵T 到目标质心的距离为R0(t)，目标的旋转角速度为Ω(t);目标上任一散射点P 点的坐标为(x，y)，该点到基阵的距离为R(t)，该点到目标坐标系原点的距离为d0= (x2+ y2)1/2，则有:

图1 ISAS 成像几何示意图Fig.1 Sketch of ISAS imaging

在t 时刻，若目标匀速转动，转动的角度为Ωt，则(x，y)点到发射基阵T的距离为:

若距离R0(t)远大于目标尺度(通常情况下均成立)，则上式可近似为［8］:

若目标质心O 不在U 轴上，仅需在上式基础上引入发射基阵T 到目标质心的视角即可。

接收基阵R 接收到P 点的回波信号可表示为:

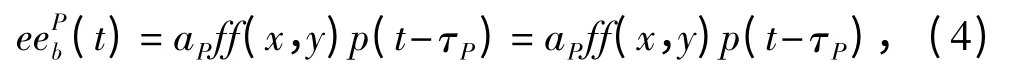
式中:p(t)为发射脉冲;τP=2R(t)/c;ff(x，y)为P点的反射系数，逆合成孔径成像即根据多脉冲回波信号重构出ff(x，y);aP为由传播和发射/接收引起的信号幅度变化因子。

P 点回波信号的基带信号为:

式中:f0为发射声脉冲信号的中心频率;* 表示卷积。

若ISAS 发射的声脉冲信号为线性调频信号LFM，则脉冲压缩后的复信号为:

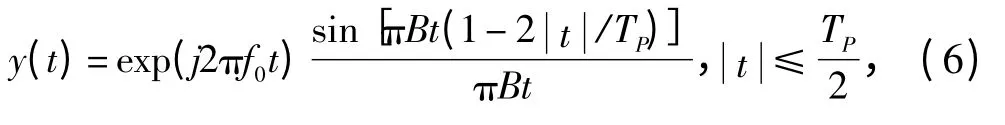
式中:TP为脉宽;B为带宽。

由式(5)和式(6)可得回波信号的基带形式为:

式中，将发射增益、接收增益、传播损失、脉冲压缩波形幅度等因素整合到幅度因子g(t)中，则总的接收信号可表示为:

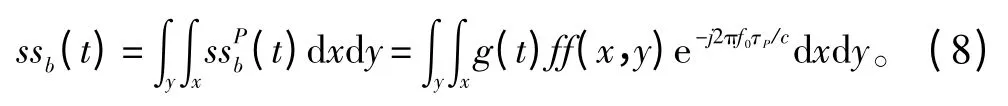
将式(3)代入式(8)，得:

式(9)等式左边可以看作是对漂移运动进行补偿后的信号，以获得高分辨目标图像。

1.2 ISAS图像重构

若忽略式(9)中幅度因子g(t)的时变性，则式(9)可以通过逆傅里叶变换来重构目标散射函数ff(x，y)，也可以通过直接数值积分的方法来实现逆合成孔径成像［8］，即转化为极坐标域内的一维积分运算，横向漂移运动补偿和视角估计误差分别体现在积分因子的幅度和相位上。

ISAS图像重构还可以采用声层析的方法［8］，声层析法可以减小运动补偿误差和目标转角不均匀所引起的图像质量下降。

文中考虑基于式(9)，采用反向投影算法进行运动目标ISAS 成像。所谓反向投影ISAS 成像，是将目标在各个运动状态上的回波信号在快速时间维进行反向追踪，分离出目标散射函数。 (注:在合成孔径处理中，由于信号的传播速度远大于基阵或目标的运动速度，因此，时间采样维又称快速时间维，而基阵或目标的运动维空间采样又称慢速时间维)。则在式(9)基础上，反向投影ISAS 成像可表示为:

先对漂移(偏移)进行运动补偿，通过式(10)才能获得较好的成像效果。若目标转动角速度不稳定，还需要对转向角速度进行补偿，即采用时变角速度Ω(t)，从而式(10)指数项中的θ 角用时变角θ(t)来代替。由于在实际的对水中目标ISAS 成像场景中，目标的运动主要体现在漂移上，因此，文中重点针对目标的漂移运动进行补偿。

2 基于亮点迹线跟踪的漂移运动补偿方法

图2为水中目标逆合成孔径成像中的目标运动误差示意图。其中，Δθ(t)为转角误差，R0(t－1)和R0(t)分别为上一时刻和当前时刻，基阵到目标质心的距离。

图2 运动误差示意图Fig.2 Sketch of kinematic error

考虑对目标漂移(偏移)运动误差进行补偿。通过逆合成孔径声呐的多次脉冲回波信号的历程图，对目标亮点信号进行距离跟踪(亮点迹线)，得到目标距离R的变化情况，根据式(3)所示的亮点到基阵距离的近似公式，可以看出，利用距离迹线中变化区间较小的亮点，即坐标接近目标坐标系原点的亮点，则式(3)的后2 项与距离相比可忽略，从该亮点迹线的距离估计值减去参考距离r0，即可得到目标的漂移运动误差的近似值。

有鉴于此，文中提出了基于亮点迹线跟踪的ISAS 运动补偿方法，具有简单易行、工程实用前景良好的特点。

3 仿真试验

建立水下目标多亮点模型如图3所示，该水下目标共由6个亮点组成，各亮点反射强度相同。发射基阵到目标坐标系的标称距离为600 m，信号为中心频率30 kHz、带宽10 kHz的LFM 信号，脉宽10 ms，ISAS 声呐对目标探测存在漂移运动误差。一次脉冲发射周期内，目标旋转0.35°。由于ISAS声呐的发射波束较宽，因而可忽略由收发波束图引起的各亮点间的幅度差异。

对图3所示的水下目标进行成像时，由于采用FFT法、声层析法［8］、波数域法［12］等会损失小部分角度空间，因此，文中采用式(10)所示的时域反向投影法，以获得最大的逆合成孔径(角度范围π)。图4为未经运动补偿的ISAS 成像结果，可见由于目标漂移运动的存在对成像结果产生较大影响。

图5为由多次回波脉冲匹配滤波后的迹线图。取第3 号迹线进行运动估计后的结果如图6所示，运动估计结果与真实值基本一致。图7为运动补偿后的ISAS 成像结果，能看出:成像后的亮点结构清晰，与目标亮点模型相当吻合。仿真试验证明了所提出的基于亮点迹线跟踪的运动补偿方法的正确性与有效性。

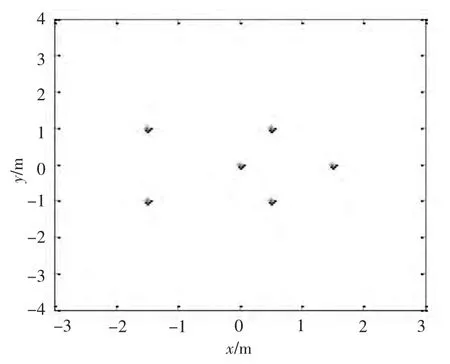
图3 目标亮点模型Fig.3 Target highlight model

图4 未经运动补偿的ISAS 成像结果Fig.4 Imaging result of ISAS without motion compensation

图5 回波迹线图Fig.5 Figure of echo traces

图6 漂移误差估计Fig.6 Drift error estimation

图7 运动补偿后的ISAS 成像结果Fig.7 Imaging result of ISAS with motion compensation

4 结 语

文中从逆合成孔径声呐的多脉冲回波图像历程上，选取对目标漂移运动补偿有益的亮点进行迹线跟踪，根据亮点到基阵距离的近似关系，估计出目标质心的漂移运动，并进行补偿，仿真试验结果验证了所提方法的正确性、有效性和可行性，能有效提高成像质量，并具有良好的工程应用前景。

［1］朱兆达.ISAR 信号处理方法研究进展［J］.逆合成孔径雷达文集，1996:83－91.

［2］保铮，朱兆达，曹志道.ISAR的进展和发展前景［J］.逆合成孔径雷达文集，1996:1－18.

［3］曹志道，刘永坦，许荣庆，等.实验ISAR 若干参数的选择和实践［J］.逆合成孔径文集，1996:20－26.

［4］王根原，等.基于匀加速多普勒模型的ISAR 成像［J］.电子学报，1997，25(6):58－61.

［5］保铮，王根原，罗琳.逆合成孔径雷达的距离－瞬时多普勒成像方法［J］.电子学报，1998，26(12):79－83.

［6］SOUMEKH M.Synthetic aperture radar signal processing with Matlab algorithms.New York:Wiley，1999.

［7］CHEN V C，MICELI W J.Simulation of ISAR imaging of moving targets［J］.IEE Proc.－Radar，Sonar Navig.，2001，148(3):160－166.

［8］VAN ZYL M W.Inverse synthetic aperture radar images of moving targets［M］.Proc.COMSIG'91，Aug.1991:42－46.

［9］PORTER N J，Tough R J A，WARD K D.SAR，ISAR and Hybrid SAR/ISAR－A unified treatment of radar imaging.Proc［J］.IEEE National Radar Conference'93，1993(4):134－139.

［10］MICHAEL M P，GOUGH P T.Synthetic aperture sonar:A review of current status［J］.IEEE J.of Oceanic Engin.，2009，34(3):207－224.

［11］WALKER J L.Range-doppler imaging of rotating objects.IEEE Trans［J］.Aerospace and Electronic Systems，1980，16:23－62.

［12］GOUGH P T，HAWKINS D W.Unified framework for modern synthetic aperture imaging algorithms［J］.Int.J.of Imaging Systems and Tech.，1997(8):343－358.