对边测量原理及其精度分析
左起奎
(河南省水利勘测有限公司,河南郑州 450008)
对边测量原理及其精度分析
左起奎
(河南省水利勘测有限公司,河南郑州 450008)
介绍了对边测量的基本原理和测量步骤,并对其精度进行分析从特殊算例中得到一般性结论,为一般的工程提供服务。
全站仪 对边测量 精度分析
科学技术的不断发展,使测量领域发生了一次又一次的技术变革。随着测量技术和测量手段的进一步提高,全站仪在今天已相当普及。
为了使全站仪在实际工作中发挥更大的效益,就要充分利用其先进的特殊功能:对边测量,偏心测量,悬高测量等。本文介绍对边测量的基本原理,并对其精度进行一定的分析。
1 测量原理
所谓的对边测量,就是指在不搬动仪器的情况下直接测量多个目标与某一起始点间的斜距,平距和高差。
以索佳(sokkia)SET500全站仪为例,测量步骤如下:
照准起始点在测量模式第1页菜单下按[距离]开始测量,待显示出测量值后按[停]停止测量。
照准目标点,在测量模式第3页菜单下按[MLM]对目标点进行测量,屏幕上显示以下各值:
S:目标点与起始点间的斜距
H:目标点与起始点间的平距
V:目标点与起始点间的高差照准下一目标点按[MLM]对目标点进行测量,同样的方法测量各目标点的斜距,平距和高差。
如图1所示:P1,P2为远处两点,为测定其水平距离和高差,可在P1,P2通视的任意点P安置全站仪,测至两点的斜距S1,S2,竖直角α1、α2,以及PP1与PP2的水平夹角β,然后根据余弦定理求得:


图1 对边测量示图
根据几何关系求得:

实际上,全站仪显示屏显示出来的平距和高差就是利用自身的内存和计算功能按式(1),(2)计算出来的。由此可见对边测量的原理简单,观测方便,特别是在P1,P2不通视的情况下更显出其优越性。
这里需指出的是按式(2)计算出的高差,既全站仪上显示出的高差并不一定就是地面点P1,P2两点的高差,而是P1,P2点反光镜中心的高差。如图2所示:

图2 高差观测略图
P1,P2两点的实际高差h12为:

式中,v1,v2分别为P1,P2点的棱镜高。显然,仅当v1=v2时式(3)才与式(2)等价。因此,在实际工作中,应尽量使两棱镜高相等,以减小计算量。否则,要加入改正数(v1-v2)。
2 精度分析
对边测量在某些情况下是很方便的,但它属于间接测距和间接测高,其成果有没有精度保证就成为研究对边测量的主要问题。
2.1 间接测距精度
设D1为P1P2间的水平距离,D2为P1P2间的水平距离。D1=S1cosα1,D2=S2cosα2则式(1)化为:
对(4)全微分得:

整理得:

由平面投影关系图看出:

在△PP1P2中由正弦定理得:

将式(6),(7)代入(5)整理得:

应用误差传播定律得:

又因为D1=S1cosα1,所以,

我们知道,cos2α1≤1,sin2α1≤1
所以,mD1
同理,mD2
将式(11),(12)代入(9)得到:

为了便于讨论,我们假设mα1=mα2=mα,ms1=ms2=ms,且β1=β2=(90°-β/2),S1=S2=S则上式变为:

由图3看出当β1=β2=(90°-1/2β)时有:


图3 平面投影关系图
将(15)代入(14),最后得到间接测距的中误差估算式:
mD2≤2sin2(β/2)(ms2+S2mα2/ρ2)+S2cos2(β/2)mβ2/ρ2(16)
为了更加直观的反映出间接测距的精度情况现在以索佳SET500型全站仪为例,其水平角一测回测角中误差mβ等于竖直角一测回测角中误差mα,即
mβ=mα=5″,使用棱镜时测距中误差,精测为:ms=±(3+2ppm·D),粗测为:ms=±(5+5ppm·D)。我们以粗测为例,因为mβ=mα式(16)化为:
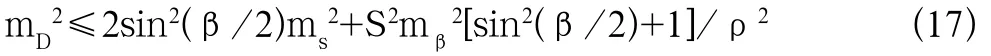
现取不同的边长S和水平角β按(17)式计算间接测距的中误差mD,见表1。

表1 对边测量水平距离精度关系表
我们可以从特殊性中推出一般性,从表中看出,当PP1与PP2之间的夹角β固定时测站离测点越近精度越高,且变化较快;当测站与测点之间的距离一定时PP1与PP2之间的夹角β越小测距精度越高,且变化较慢。
结论:(1)当全站仪选定后,即测角、测距精度一定后,间接测距的精度主要取决于测站与测点之间距离,越小精度越高。(2)间接测距具有较好的精度,能满足地形测量、地籍测量及一般工程测量的要求。
2.2 间接测高的精度
将(2)微分得:

将上式转化为中误差关系式:

令S1=S2=S,α1=α2=α则mS1=mS2=mS,mα1=mα2=mα。
则(18)式变为:

仍以索佳SET500型全站仪为例,取不同的S和竖直角α,按(19)计算间接测高的中误差mh,见表2。

表2 对边测量高差精度关系表
观察表2可知,对于索佳SET500全站仪来说,当测点到测站的距离在 0--300m变化时,竖直角越大高差中误差越大,在大于300m的情况下竖直角越大高差中误差越小。
结论:(1)测点到测站的距离是影响高差精度的主要因素。(2)当边长S在300m之内变化时,竖直角越大高差中误差越;当边长S大于300时,竖直角越大高差中误差越小。(对于不同的型号的全站仪S的取值可能不同)
3 结语
全站仪的普及使用,大大提高了外业工作的效率,特别是它具有的一些特殊功能,使过去很难完成的测量变的简单,为测量作业提供了极大的方便。对边测量只是一个很好的例子。掌握影响对边测量的测距、测高精度因素,可以选择适宜的测站,采用必要的测距,测角精度,以保证测距和测高结果的精度满足工程的要求。
[1]郭宗河,吴叶美.对边测量的精度分析.测绘工程,1998,9.
[2]焦明连.间接测距精度.测绘工程,1995,6.
[3]樊功瑜.误差理论与测量平差.同济大学大学出版社,1998、4.
[4]邵自修.工程测量,冶金工业出版社,1999,5.
[5]陈在贵.测量工程.四川科学技术出版社,1998,4.
This article introduce the basic principle and surrey prcoedure of RDM,and analyses its accuracy.Get some gengeral conclusions from the special example.Some services are offered for gengeral project.
Total-station intruments RDM Accuracy analysis
左起奎,男,工程师,1992年毕业于郑州测绘学校,2008年在华北水利水电学院深造,是单位技术革新的主力军,主持或参与的水利勘测工程多次获得省、部级一、二等奖。

