基于支持向量回归机算法的海水富营养化过程中藻类繁殖状态软测量研究

张颖，高倩倩，高茂庭

（上海海事大学信息工程学院，上海201306）

1 引言

近几年，经济的快速发展使得工农业生产的规模不断扩张，导致环境污染日趋严重。大量富含氮、磷、铅的排放物最终流入大海，海水的富营养化程度日益严重，导致赤潮等灾害频繁发生[1]，使得海洋生态环境日益恶化，给海洋周边的人类生活带来严重危害。大量的研究结果表明，海水的富营养化与海水中藻类的生长繁殖密切相关，但是问题的复杂性在于：藻类的快速繁殖生长并不是简单地和某些排放物质含量的增加呈线性递增的关系，导致藻类爆发性繁殖的条件非常复杂，研究表明，藻类的生长与海水的硝酸盐含量、海水盐度、溶解氧含量、温度、海水浑浊度等十几个理化因子的变化密切相关[2]。海水中的叶绿素-a浓度是体现水体中生物量含量的综合指标，目前多数研究人员将叶绿素-a的浓度作为反映海水中藻类繁殖状态的重要表征指标[3-4]。通过分析叶绿素-a浓度的变化，可以获取海水中藻类生物量状况及其变化趋势，达到对海水富营养化的有效监测[5]。

软测量是一种以软件算法为主的测量手段,与传统意义上的传感器不同,软测量所测量的参数一般不是某个特定的物理/化学参量,而是针对具体的应用问题，采用较易直接测得的辅助测量变量，通过数学模型的计算，得到难以测量或者根本无法测量的关键变量值。由于影响海水中叶绿素-a 浓度的因素众多，且相互作用复杂，直接在线测量比较困难，离线测量则需要昂贵的分析仪器，且不能保证测量的实时性。采用软测量方法间接推断其在海水中的含量可以较好地解决这一测量技术难题[6]。目前建立软测量模型的方法主要有：BP神经网络算法、模糊神经网络算法、经验预测法、多元回归分析方法等。本文采用支持向量回归机算法（SVR）对海水叶绿素-a浓度进行软测量，以期达到具有较好稳定性和精确性的软测量效果。

支持向量回归机算法（SVR）[7-8]是建立在统计学习理论的VC 理论和结构风险最小化原理之上的，根据有限的样本信息，在模型的复杂性和学习能力之间寻求最佳折中，以获得最好的泛化能力——推广能力。与其他的研究方法相比，该方法能更好地优化各参数，避免局部最优解，具有较好的全局收敛性。

2 支持向量回归机算法

2.1 算法描述

由于SVR算法具有过拟合现象少、对于特征过多所造成的维数灾难不明显、易收敛于全局解、核函数使用灵活等优点，所以SVR 算法在解决小样本、非线性、高维模式识别以及函数拟合等问题中得到广泛的运用[9]。

非线性支持向量机回归的主要思想是：通过适当的核函数wx+b=0 将低维空间中数据x映射到高维特征空间，并在这个空间进行线性回归。如图1所示。

根据结构风险最小化原理，SVR 算法在学习过程中主要是折中考虑降低样本的经验风险（训练误差）和最小化置信范围（结构复杂度带来的风险）。SVR算法学习过程的目的是线性回归，即对可用的独立同分布数据进行处理，找到一个函数f(x)可近似为y(x)值,即估计数据：

若在ε 精度下，函数f(x)不能估计所有(xi,yi)数据，则引入松弛变量ξ ，那么寻找最小w 的凸优化问题可以最终归为解下面二次规划的问题：

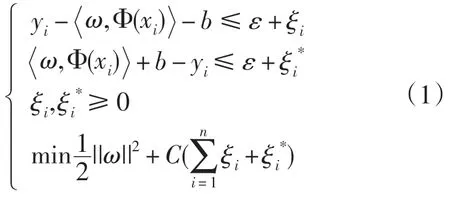
式中，常数C（C>0）作为惩罚因子，用来平衡经验风险和置信范围的比例。

非线性回归函数为：

图1 原始空间向高维特征空间映射

入拉格朗日函数和对偶变量，如下所示：

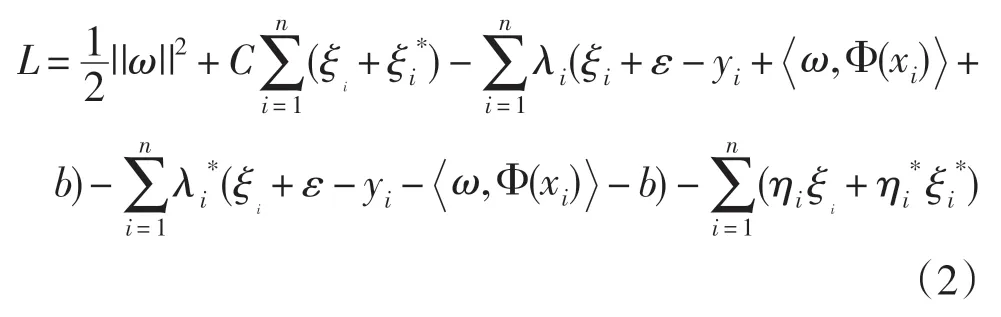
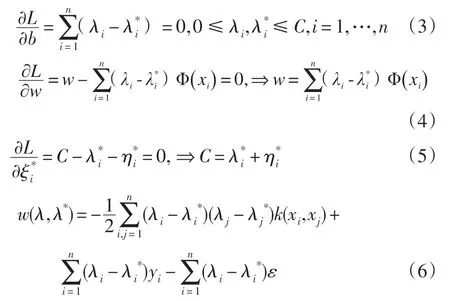
在（3）式约束条件下，其中由（4）式得到w，将（6）式最大化求出参数的值，最后将w 的值带入非线性回归函数中，可以表示为：

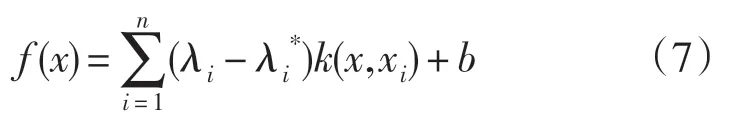
2.2 支持向量回归机的模型构造

本文对反映海水藻类繁殖状态的海水叶绿素-a浓度软测量模型的构造采用如图2所示的形式。

首先，采用灰色关联分析法对原始数据进行关联性分析，提取与叶绿素-a浓度关联度较大的环境因子作为主控辅助变量。然后选定训练集和测试集，并使用SVR 算法对训练集进行训练，最终用得到的模型对测试集进行预测，并分析预测结果的均方差。

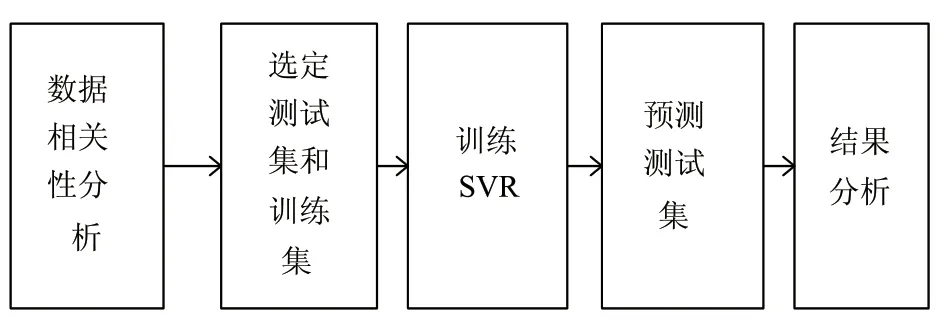
图2 模型构造流程图

根据SVR 算法的思想，本文使用如图3 所示的支持向量回归机体系结构图对叶绿素-a 浓度进行软测量，其中x1，x2，…,xi表示本文采用灰色关联分析后得到的主控辅助因子，k(x,xi)表示核函数[10]，本文采用的核函数为径向基核函数（RBF)，表示为：

式中，xi为核函数中心，σ 为函数的宽度参数，控制函数的径向作用范围。

3 主要辅助因子的选择

3.1 灰色关联分析法概述

灰色关联分析（Grey Relational Analysis，GRA）方法是分析系统之间相似或相异的关联程度，主要用于分析系统各因素之间相关特征，从而挖掘出系统的主要影响因素[11]。灰色关联度是两个系统或两个因素间关联性大小的量度，它描述系统发展过程中因素间相对变化的情况，在一个系统中的两种因素，如果在发展过程中相对变化态势一致性较高，则两者的灰色关联度较大；反之，灰色关联度就较小。本文采用灰色关联分析方法，分别分析各个辅助影响因子与主因子（叶绿素-a 浓度）之间的关联程度，选择与主因子关联度较大的几个因子作为输入变量，从而在保留原始数据大部分信息的情况下，保证预测的有效性。

3.2 数据来源及描述

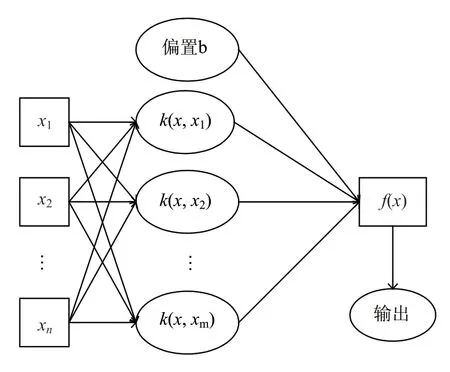
图3 支持向量回归机的体系结构

本文选取的数据是从长江口南汇嘴近海海域布置的采样点连续采集的观测数据，时间是从2012年3月15日至2012年5月15日，从中选取300组水环境相关数据作为本次实验的样本数据。根据历年这一海域海洋环境因子观测资料可知，上述时间段也是这一海域藻类繁殖状况异常的多发季节。每组数据分别包括：温度、溶解氧含量、硝酸盐含量、透光度、酸碱度、叶绿素-a 浓度、传导率、盐度8个因子，并采用灰色关联分析法分别对8 种因子进行相关性分析，从而得到叶绿素-a 浓度与其它7 个影响因子的相关度。根据各个影响因子的相关度，从300 组数据中提取出主控因子，并将其1—200 组数据作为训练集，对SVR 神经网络进行训练，得到训练模型；将其201—300 组数据作为测试集，并使用训练得到的模型对其进行预测。

3.3 数据相关度分析

由于叶绿素-a 浓度是表征水体富营养化程度的典型指标之一，所以，本文将叶绿素-a 浓度作为主因子（x0），其余7个因子作为影响因子，包括：温度TP（x1）、溶解氧DO（x2）、酸碱度PH（x3）、盐度SA（x4）、传导率CO（x5）、光强度LI（x6）和硝酸盐含量NI（x7）。采用灰色关联分析法进行数据相关度分析，本文将相关度大于0.65的影响因子作为主控因子。这样做的目的是在保留原始数据大部分信息的情况下，保证预测的有效性。

数据相关度分析步骤如下：

步骤1：由于在实际问题中，不同的影响因子往往具有不同的量纲，而在计算关联系数时，要求量纲相同，因此，需要对各个影响因子做初始化处理，无量纲化处理方法表示为：

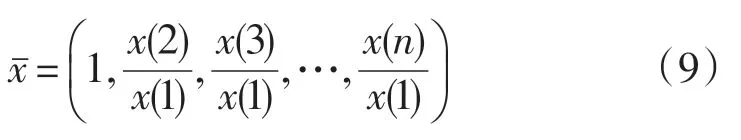
步骤2：选取主因子序列，表示为：

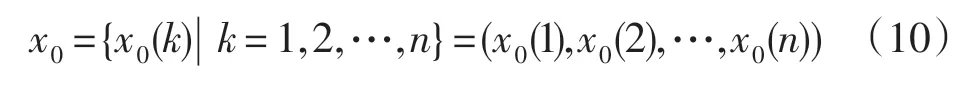
式中，k 表示数据个数，x0表示叶绿素-a浓度，n=300。由于数据是根据时间序列来记录的，也可以代表时间序列，本文为了方便说明，把k 作为时刻来论述。

步骤3：选取影响因子序列，表示为:

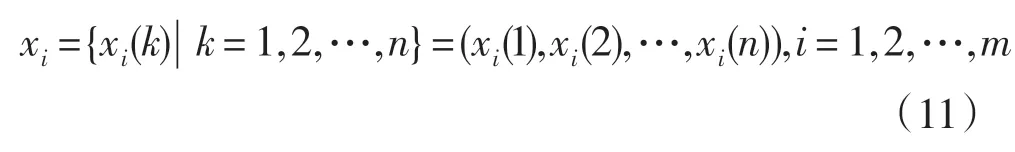
式中，m 代表环境影响因子个数，由于本文研究的影响因子有x1、x2、x3、x4、x5、x6、x7，所以m=7。

步骤4：计算关联系数，计算公式表示为：

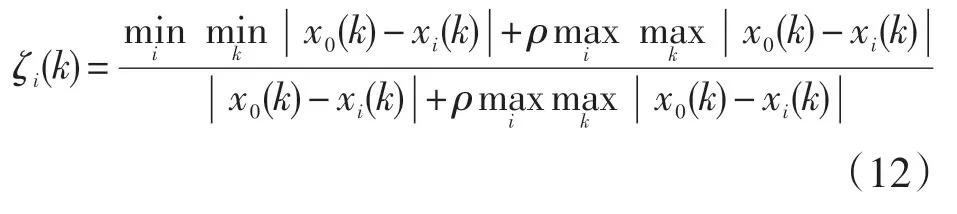
式中，ζi(k)为影响因子序列xi对主因子列x0在k 时刻的关联系数，ρ 为分辨系数（ρ ∈[0,1]），本文取ρ=0.5。

步骤5：由公式5 可以得到300 个相关系数，由于300个信息过于分散，不便于比较分析，为此本文对关联系数进行平均化处理，计算公式为：

式中，ri为辅助影响因子序列xi对主因子序列x0的关联度。根据上述步骤，可计算出辅助影响因子（x1¯ x7）与主因子叶绿素-a（x0）浓度之间的相关度，结果如图4所示。

图4以柱形图的形式直观的显示了个影响因子与主因子之间的相关度，其中1—7 分别代表温度、溶解氧含量、酸碱度、盐度、传导率、光强度和硝酸盐含量与叶绿素-a浓度的相关度。

由图4 的结果分析可知：温度、含盐量与叶绿素-a 浓度的相关度均在0.2 左右，传导率与其的相关度只有0.0898，所以可以忽略这3 个子因素对叶绿素-a 浓度的影响。溶解氧含量、酸碱度、光强度和硝酸盐量与叶绿素-a 浓度相关程度均大于0.65，因此，本文将溶解氧含量、酸碱度、光强度和硝酸盐含量作为软测量训练模型的输入因子。

图4 相关度柱形图

4 基于SVR的叶绿素-a浓度软测量

根据灰色关联分析法处理后的结果，将溶解氧、酸碱度、光强度和硝酸盐量作为训练模型的输入因子，选取叶绿素-a 浓度(μg/L)作为模型唯一的输出因子。

根据上述样本数据、基于SVR 算法进行叶绿素-a浓度软测量模型的建模,其结果如图5和图6所示。图5是利用样本数据进行学习建模的结果，图6是针对建模结果进行软测量测试验证的结果。

针对相同的样本数据，应用T-S 模糊神经网络进行软测量模型建模的结果如图7 和图8 所示，其中，图7 是利用样本数据进行学习建模的结果；图8是针对建模结果进行软测量测试验证的结果。应用BP 神经网络进行软测量模型建模的结果如图9和图10 所示，其中，图9 是利用样本数据进行学习建模的结果，图10是针对建模结果进行软测量测试验证的结果。

针对三种算法的测试结果进行均方误差比较如表1所示。

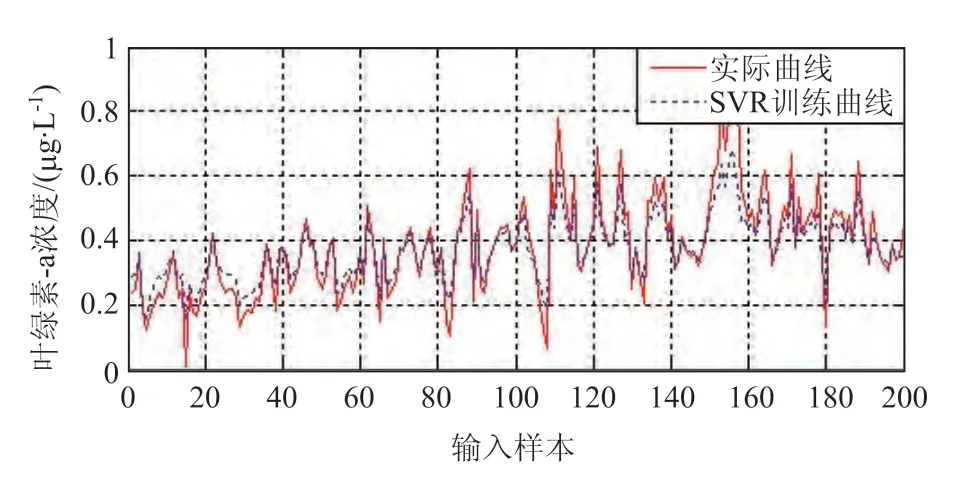
图5 基于SVR方法的样本训练

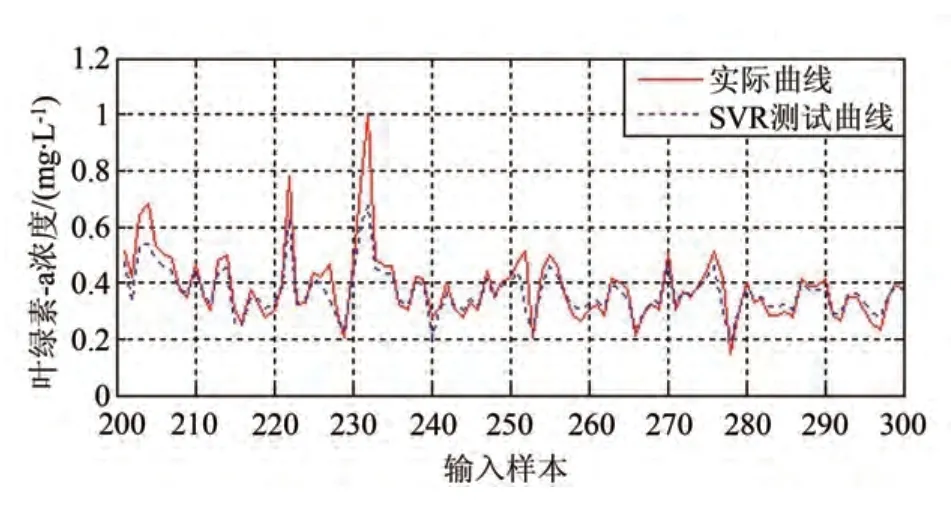
图6 针对SVR模型的泛化性测试

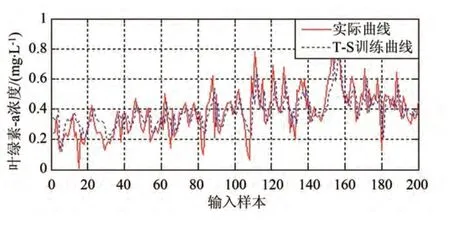
图7 基于T-S模糊神经网络的样本训练

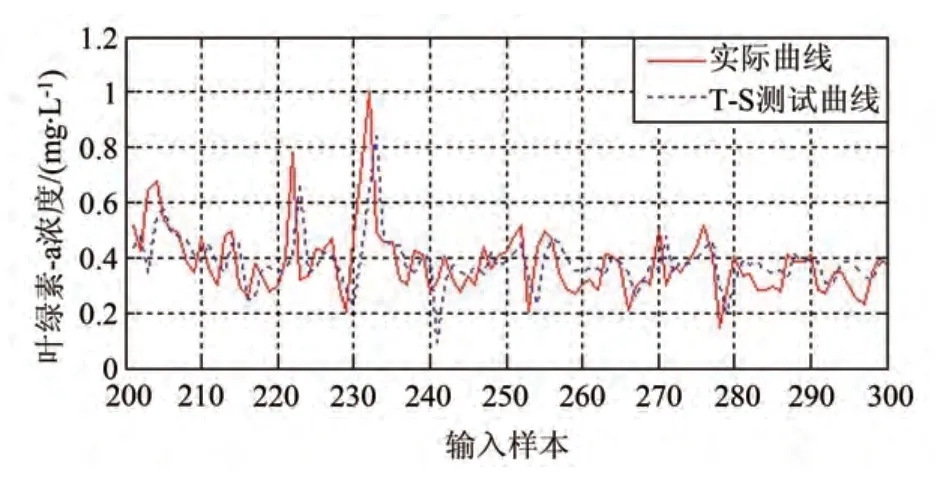
图8 针对T-S模糊神经网络的泛化性测试

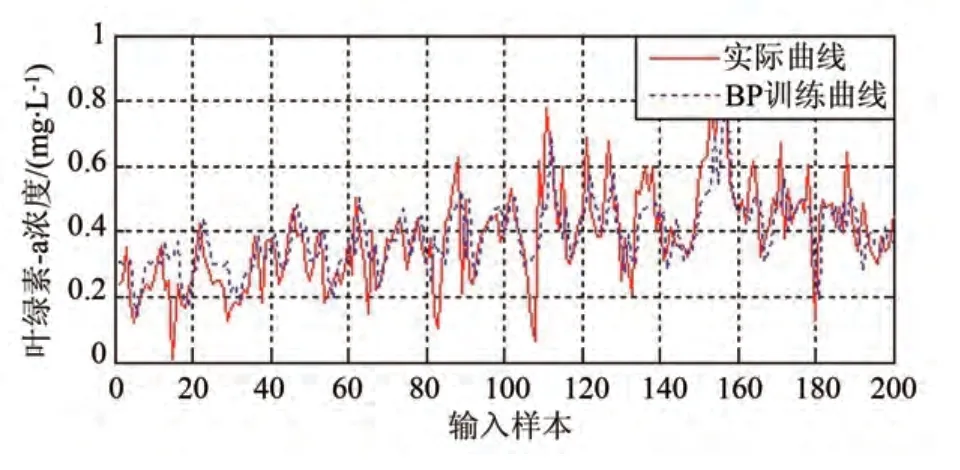
图9 基于BP神经网络的样本训练

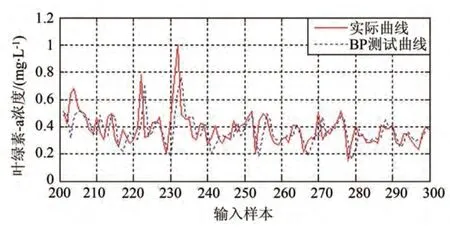
图10 针对BP神经网络的泛化性测试

表1 几种算法的测试均方误差比较

从表1 可以看出，SVR 算法的精确度最高，T-S模糊神经网络虽然也能达到一定精度，但是其算法较SVR 复杂，占用系统资源较大。BP 神经网络则误差较大，实际中还存在学习收敛稳定性欠佳的问题。

SVR方法具有较好的样本学习收敛性，模型稳定可靠，运算量适中，适合于在线辨识学习及模型在线校正。通过实验可以发现，针对这一海域的观测数据，上述方法具有较好的软测量建模及测试验证效果，它表明在这一海域条件下，上述方法是适合于针对海水藻类繁殖状态进行软测量预估的。此方法可对类似状态下海水环境关键理化因子的软测量提供借鉴。

5 结束语

大量研究表明，海水富营养化过程中大量繁殖的鞭毛藻等藻类植物的主要表征生物量即是叶绿素-a，因此，海水叶绿素-a 浓度可以有效反映海水藻类的繁殖状态，叶绿素-a浓度越高说明藻类在该水域繁殖越快。本文旨在提供一种用于实时获取海水叶绿素-a浓度的软测量方法，它提供了一种间接获取藻类繁殖状态信息的途径。籍于此还需要后续开展针对藻类繁殖状态评估方法等研究工作。

SVR 的最终决策函数是由其获得的支持向量所确定的，计算的复杂性取决于这些支持向量的数目，而不是样本空间的维数。通过融合灰色关联分析法针对数据样本进行相关度分析，可以实现针对软测量模型进行降维的目的。本文将数据预处理与软测量模型构建相结合，将筛选出的主要辅助变量作为软测量模型的输入变量，将反映海水藻类生物量指标的叶绿素-a 浓度作为软测量模型输出变量，实现了针对海水藻类繁殖状态软测量的目的。

[1]王冬云,黄焱歆.海水富营养化评价的人工神经网络方法[J].河北建筑科技学院学报,2001,18(4):27-29.

[2]张丽旭，张小伟.用于海洋环境科学的一种新方法—影响因子分析法[J].海洋科学进展，2004,22(1):33-36．

[3]Lee J H W, Huang Y, Dickman M. et al. Neural network modelling of coastal algal blooms [J]. Ecological Modelling, 2003, 159(2):179-201.

[4]Melesse A M, Krishnaswamy J, Zhang K Q. Modeling Coastal Eutrophication at Florida Bay using Neural Networks[J].Journal of Coastal Research,2008,24(2):190-196.

[5]郑丙辉,张远,富国,等.三峡水库营养状态评价标准研究[J].环境科学学报,2006,26(6):1022-1030.

[6]李雪,刘长发,朱学慧,等.基于BP 人工神经网络的海水水质综合评价[J].海洋通报,2010,29(2):225-230．

[7]Vapnik V, Chapelle O. Bounds on error expectation for support vector machines[J].Neural Computation,2000,12(9):2013-2036．

[8]Abe S，Inoue T. Fuzzy support vector machines for multiclass problems[C]. ESANN’2002 Proceedings- European Symposiumon Artificial Neural Networks,Bruges,Belgium,2002:113-118.

[9]Zaiwen L, WANG X, Lifeng C, et al. Research on Water Bloom Prediction Based on Least Squares Support Vector Machine[A].2009 World Congress on Computer Science and Information Engineering[C].LosAngeles,2009:764-768.

[10]李琳,张晓龙.基于RBF 核的SVM 学习算法的优化计算[J].计算机工程与应用,2006,29:190-192,204.

[11]王红瑞,闫五玖.环境质量的模糊综合评判—灰色关联分析复合模型及实例分析[J].北京师范大学学报,1997,20(4):39-43.