一种自主研磨作业机器人动力学仿真

王文忠

（长春工程学院工程训练中心，长春130012）

模具的研磨过程是直接影响到产品的最终质量的重要工艺过程，目前手动研磨是数控铣削后的金属模具的主要精加工过程，该过程需要专门的技术和工时。因此，需要提高其效率和质量稳定性。为了解决目前存在的问题，有学者开始了研磨大型自由曲面的轮式微小机器人在研究［1］，为了实现用微小机器人研磨大型模具自由曲面，本文设计了一种可研磨整个待加工自由曲面的5轴联动自主研磨机器人。该机器人结构由直角坐标机构、转动机构和摆动机构构成（如图1所示），工作方式类似一个5轴数控机床的工作过程。

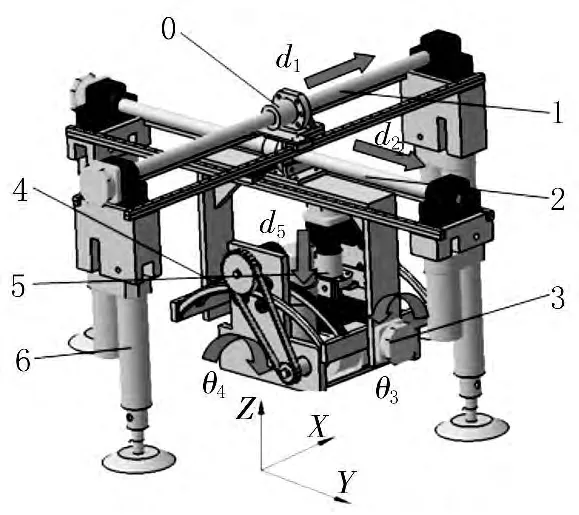
图1 移动机器人结构

目前进行机器人动力学分析的方法有很多种，如 Lagrange，Newton－Euler，Gauss，Kane，Motor，Roberson－Wittenburg等方法［2－4］。本文首先运用Lagrange法建立了机器人动力学模型，然后利用Matlab软件平台进行了运动学及动力学仿真［5－8］，最后总结了仿真结果。

1 机器人的动力学模型

1.1 坐标系统

自主研磨机器人的运动学逆解坐标系如图2所示，基坐标系O0－x0y0z0设置在移动平台上，其坐标原点设置在X方向运动与Y方向运动连接质心处，确定X方向运动的坐标系O1－x1y1z1，确定Y方向运动的坐标系O2－x2y2z2，坐标系O3－x3y3z3设置在转动机构上，坐标系O4－x4y4z4设置在摆动机构上，坐标系O5－x5y5z5设置在研磨工具头上。

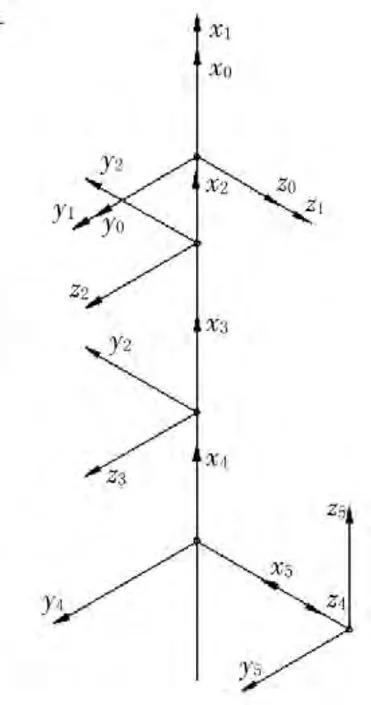
图2 坐标系

1.2 广义坐标

根据5轴联动的结构特点，移动平台实现X方向和Y方向运动，转动机构实现绕y3轴的转动，摆动机构实现绕y4轴的摆动，所以系统广义坐标为

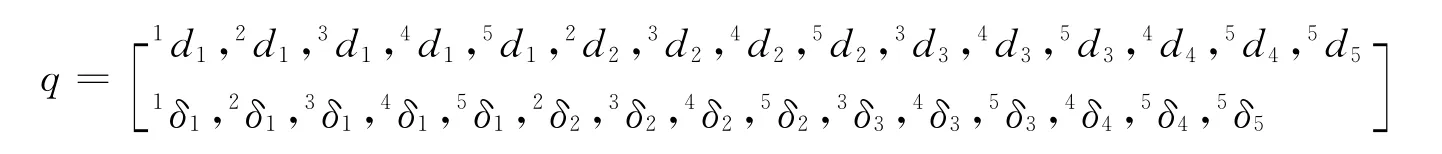
1.3 约束方程的建立

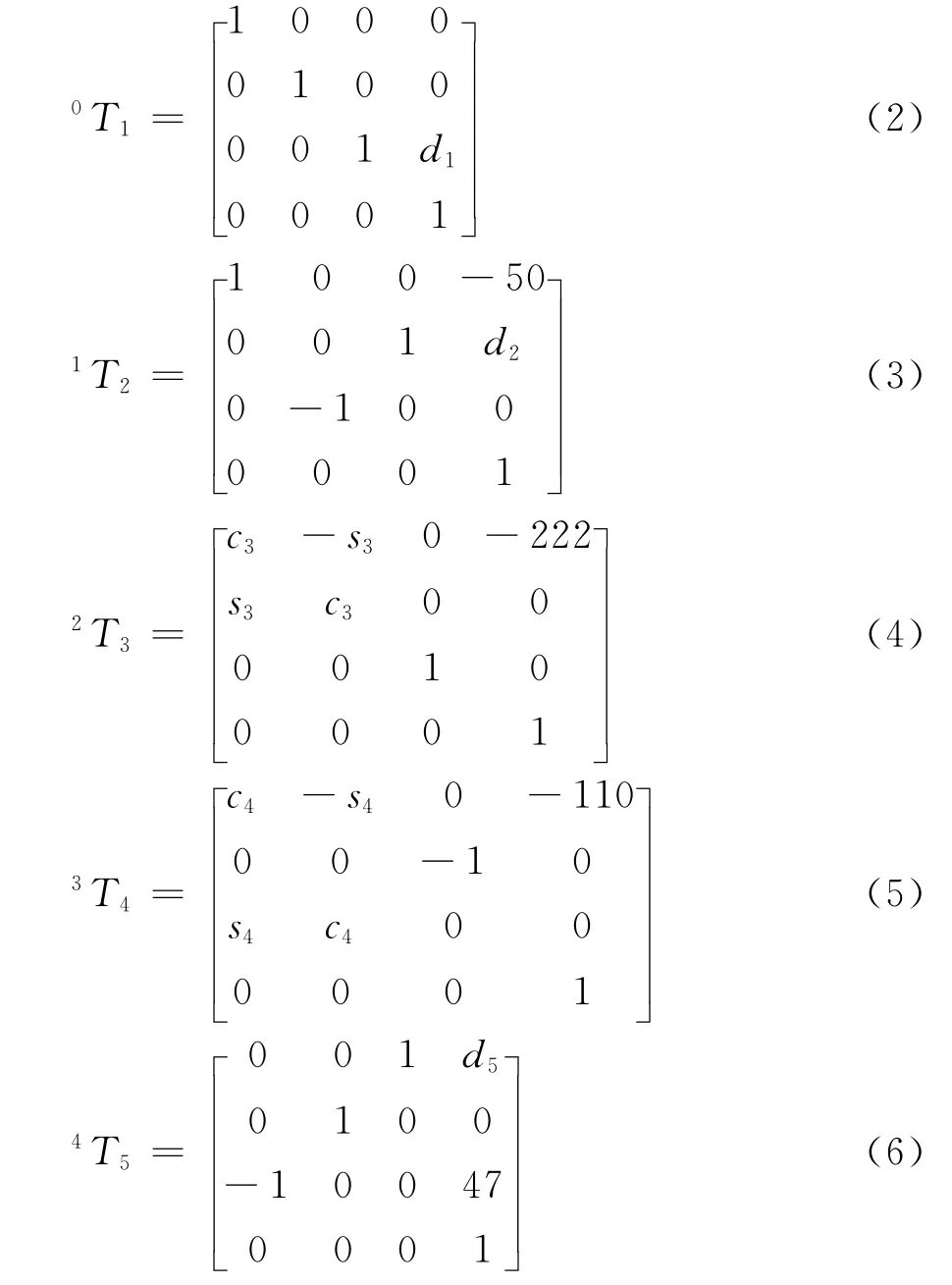
从坐标系O5－x5y5z5到坐标系O0－x0y0z0的变换矩阵，可由式（1）计算得到。

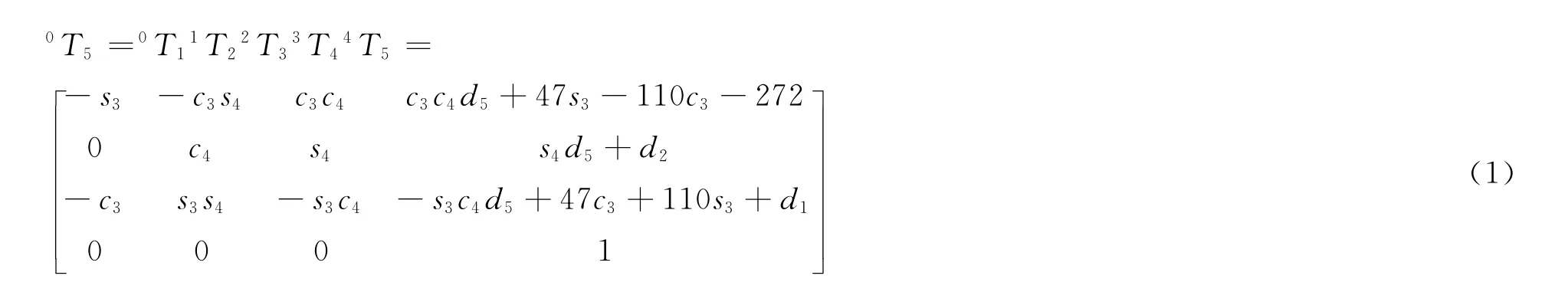
从坐标系O－xi＋1yi＋1zi＋1到坐标系O－xiyizi（i＝0，1，2，3，4）的变换矩阵iTi＋1如公式（2）～（6）所示，矩阵中的S和C分别表示正弦和余弦函数。

1.4 Lagrange方程［9－12］

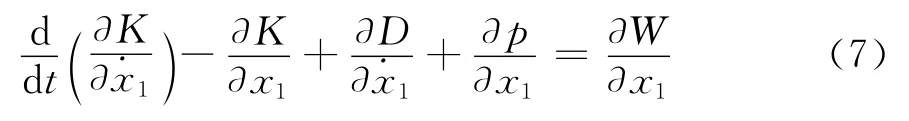
1.5 动力学建模［10］

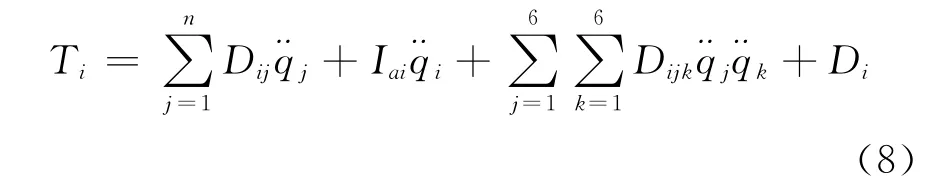
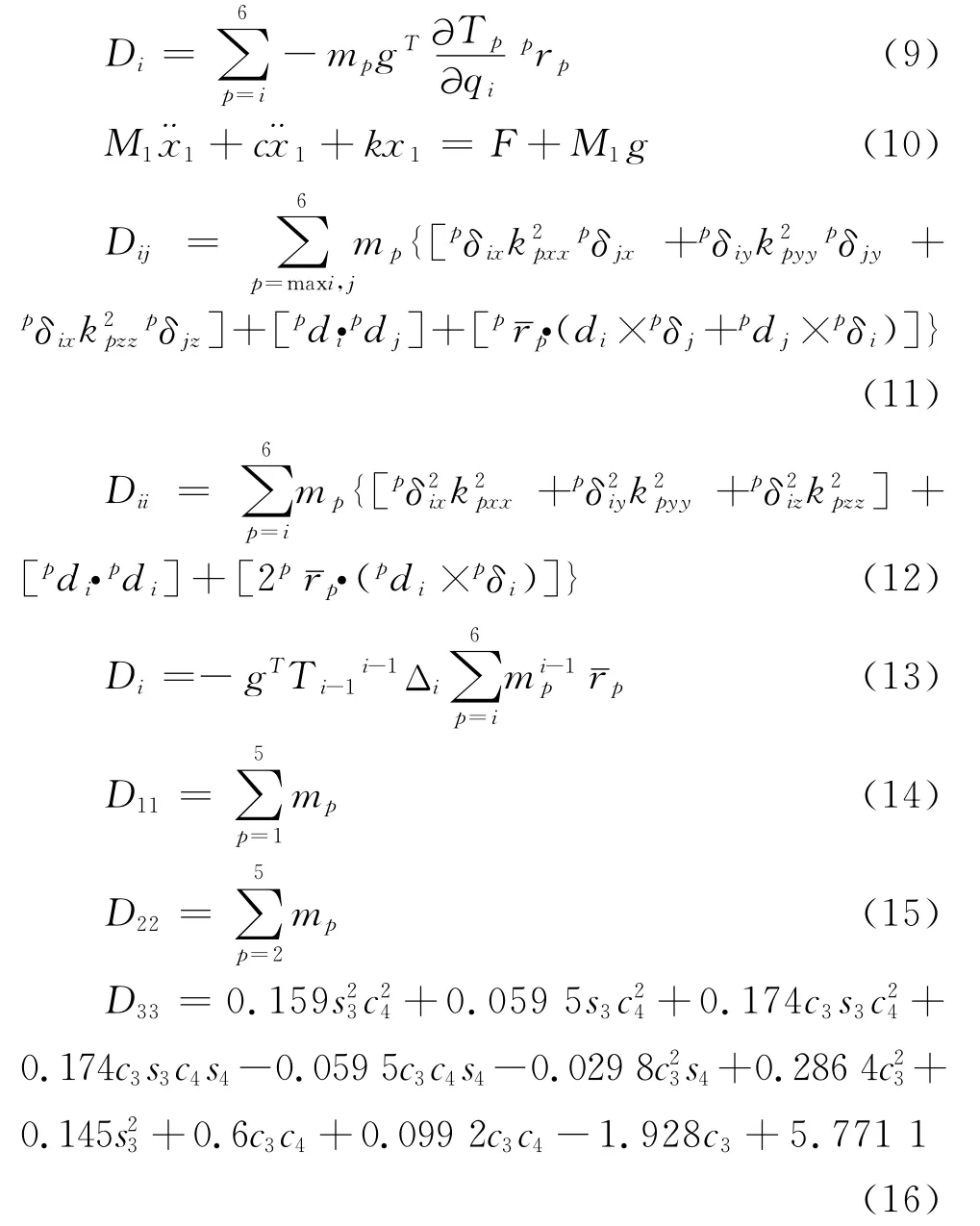
省略其他复杂的变换表达式。

2 数值仿真

2.1 运动学及动力学仿真

机器人的主要动力学参数（质量惯矩）如下：

质量参数

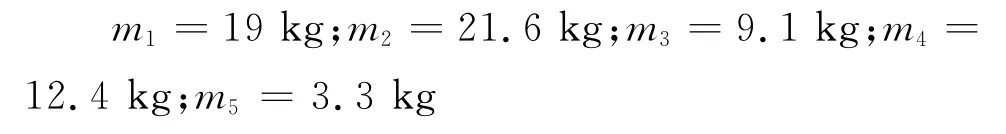
转动惯量

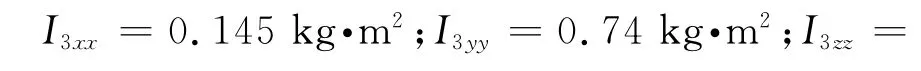
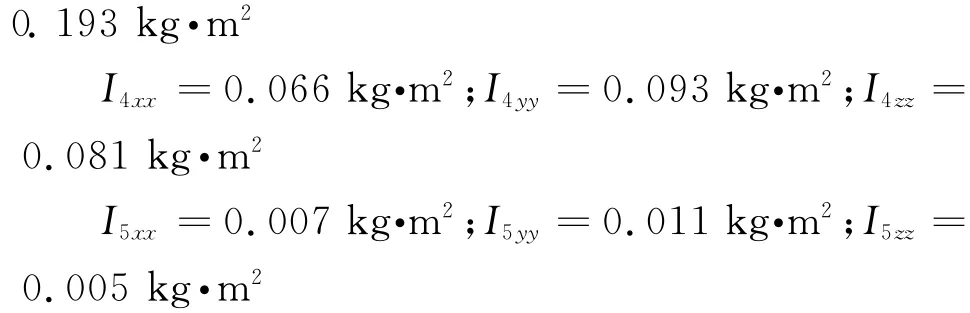
曲线路径

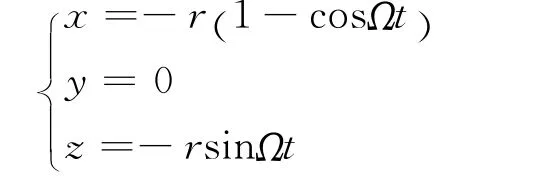
其中半径r＝40mm；仿真时间t＝0～20s；角速度Ω＝2°／s。

工具头末端轨迹如图3所示。

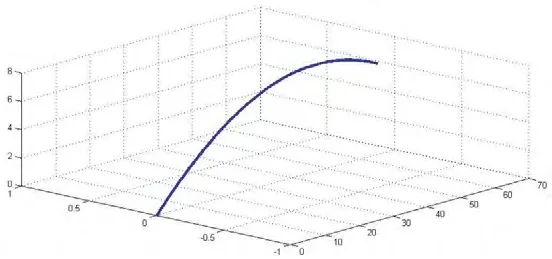
图3 工具头末端轨迹

2.2 仿真结果分析

经数值仿真，得到串联机器人对应构件节点的速度和角速度曲线、加速度和角加速度曲线、驱动力和力矩曲线，如图4～8所示。

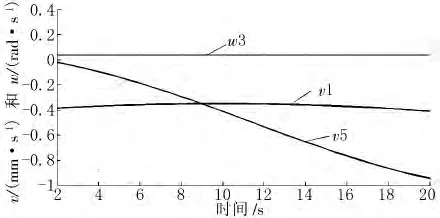
图4 关节O1，O3和O5的速度与角速度

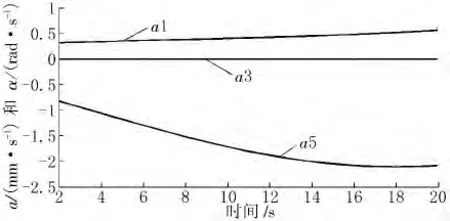
图5 关节O1，O3和O5的加速度

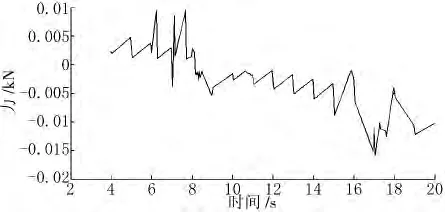
图6 关节O1的力仿真

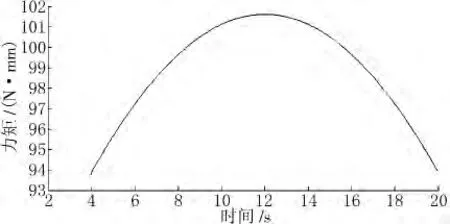
图7 关节O3的驱动力矩

图8 关节O5的力仿真

从所得的仿真曲线可以看出，机器人做如图3所示的轨迹运动时，驱动关节3和5的运动平稳，对电机也没有力矩的冲击，在加速与减速阶段，作用在关节1上的力存在波动和冲击。验证了文中自主研磨机器人的动力学稳定性，可以通过改变各关节驱动力矩来控制机器人各机构的运动和整体的运行状态。

3 结语

自主研磨机器人的运动学和动力学分析，解决了运动学的正、逆解问题。应用Lagrange法进行了动力学建模与计算，首先建立了机器人的Lagrange方程，然后获得了各部分的关联矩阵，最后实现了数值仿真。该方法所建立的动力学模型，计入了各运动构件的动力学计算，适合本文的自主研磨机器人建模。验证了自主研磨机器人的模型和分析是可行的，为进一步优化该机器人的运动学和动力学及控制系统仿真提供了依据。

［1］Chen G L，Zhao J，Zhang L，etc.Researching of a wheeled small polishing mobile robot for large freeform surface and its kinematic［C］／／Proceedings of the 8th International Conference on Frontiers of Design andMa－nufacturing.Tianjin：ICFDM，2008：341－345.

［2］William M Silver.On the equivalence of largrangian and newton－euler dynamics for manipulators［J］.The Intern.Honrnat of Robotics Research，1982，1（2）：60－70.

［3］Li J L，Lv T S.Study of dynamic stable control for a Leg－wheeled robot［J］.Journal of Harbin Institute of Technology：New Series，2006，13（1）：43－47.

［4］Kane Thomas R，Levinson David A.The use of kane's dynamical equation in robotics［J］.The Intern.Conf.on the Canada，1983，2（3）：3－21.

［5］Ibrahim Ouarda，Wisama Khalil.Inverse and direct dynamic models of hybrid robots［J］.Mechanism and Machine Theory，2010，45：627－640.

［6］Altuzarra Oscar，Zubizarreta Asier，Cabanes Itziar，etc..Dynamics of a four degrees－of－freedom parallel manipulator with parallelogram joints［J］.Mechatronics，2009，19：1269－1279.

［7］Schöner G，Dose M，Engels.Dynamics of behavior：Theory and applications for autonomous robot architectures［J］.Robotics and Autonomous Systems，1995，16：213－245.

［8］Kemal Ider S.Inverse dynamics of parallel manipulators in the presence of drive singularities［J］.Mechanism and Machine Theory，2005，40：33－44.

［9］刘延斌，韩秀英，薛玉君，等.3－RRRT并联机器人动力学仿真［J］.系统仿真学报，2006，18（7）：1962－1965.

［10］Armstrong B.The explicit dynamic model and inertial parameters of mobile robots［C］／／Proc.Of 16thISIE.Brussels，Belgium：ISIE，1986：483－490.

［11］蔡自兴.机器人学［M］.北京：清华大学出版社，2009.

［12］Bhaskar Dasgupta，Mruthyunjaya T S.Anewton－euler formulation for the inverse dynamics of the stewart platform manipulator［J］.Mechanism and Machine Theory，1998，33：1135－1152.