完全二部有向图的(，α)-因子分解

朱 莉，陆 健

(南通职业大学 基础部，江苏 南通226007)

0 引言

Km，n是完全二部图，其两个部分点集分别具有m和n个点表示对称的完全二部有向图，它是由Km，n的每条边替换成方向相反的两条有向弧而的到的有向图表示2k长有向圈，其点集为向弧集为－因子是的一个子图F，其满足(1)F的有向弧集可分解为若干个有向圈，(2)的每一个点都恰好出现在 F 的α个中。如果的有向弧集可以划分为－因子的和，则称存在，α)－因子分解，或称可－因子分解。本文用到图论方面的名词术语均参照图论著作［1］或［2］。

1 主要结论

证明:记 λKm，n和 Y 是的两个部分点集，且 | λKm，n|=m，|Y|=n。设的一－因子分解，其中Fi(1≤i≤r)是－因子。在每一个－因子 Fi(1≤i≤r)中，λKm，n中的每一个点和Y中的每一个点均出现α次。由 λKm，n中点计算－因子分解中，有－因子数得 r=n/α，再由 Y 中点计算，α)－因子数得 r=m/α，它们应该相等。所以有，m=n ≡0(mod α)。在每一个－因子中，的数量有，即 b=nα/k。由 r和b的表达式，我们可得m=n≡0(modαk/d)，其中d是α和k的最大公约数。必要性得证。

证明:设{F1，F2，...，Fs}是Ks，s的一个1－因子分解(其存在性见文献［1］)，其中 Fi(1≤i≤s)是 Ks，s的 1－因子。再设，其中的边。将 Ks，s的每一个点加权n，每条边ei，j看作是一个。由题设，令相对应－因子分解，其中是相对应－因子。则对于每一个是的一个－因子，而即是－因子分解。得证。

证明:令λKm，n和Y是的两个部分点集，且

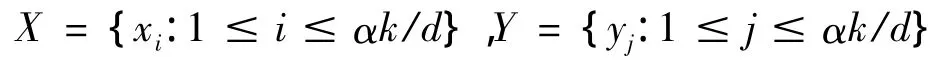
约定 xi和 yj的下标在{1，2，...，αk/d}进行模 αk/d 的运算。

对于任意1≤j≤n+1，构造如下有限圈

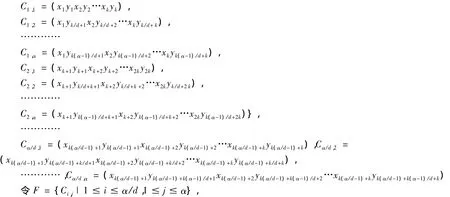
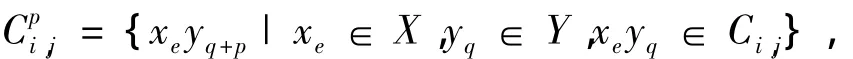
则可以验证每一个Fp(p∈Zp/d)都是－因子，且它们并集正好构成。从而，{Fp|p∈Zp/d}是－因子分解。

［1］Harary F.Graph Theory［M］.Massachusetts:Addison-Wesley，1969.

［2］Chartrand G，Lesniak L.Graphs＆ Digraph［M］.2nded，California:Wadsworth，1986.

［3］Jungnickel D，Mullin R C，Vanstone.The spectrum ofα-resolvable block designs with block size 3［J］.Discrete Math，1991，97(4):269－277.

［4］Zhang Y，Du B.α-resolvable group divisible designs with block size three［J］.Combin.Designs，2005，13(1):139－151.

［5］Ma X W，Tian Z H.α-resolvable cycle systems for cycle length 4［J］.Journal of Mathematical Research＆ Exposition，2009，29(6):1102－1106.