螺旋桨环流理论(升力线理论)设计
侯 奕,孙江龙,吕续舰
(华中科技大学 船舶与海洋工程学院 船舶和海洋水动力湖北省重点实验室,湖北 武汉430074)
0 引 言
船舶螺旋桨的设计经历了基于模型系列试验的图谱设计、升力线和升力面理论设计与计算和格林函数法理论设计与计算的不同发展阶段[1]。其中,升力面理论的应用日趋完善。而升力线理论设计结合升力面理论修正,可以较为便捷地提供初步数据以供参考和估计,因此基于升力线理论的螺旋桨设计依然具备其自身优点和使用价值。
在实际应用中,螺旋桨环流理论(升力线理论)设计有2 种方法:一种为近似法,即哥尔斯坦函数法;另一种为精确法。本文分别在近似法与精确法中应用了Morgan[2]与Lerbs[3]的理论和方法。一般说来,与近似法相比,精确法使用诱导因子对切向和轴向诱导速度等参数进行求解,对螺旋桨设计问题能够给出许多精确的解。而近似法设计计算简单,能够给出与精确法计算相比相当一致的结果。本文通过对比分析2 种设计方法计算得到的对应数据,验证了这一点。
1 基本理论
1.1 近似法
在螺旋桨升力线理论设计过程中,引入了一些假定:螺旋桨的尾流不收缩,忽略径向诱导速度,总的诱导速度与入流速度垂直等。按照上述假定,轴向和切向诱导速度之间有简单的三角关系表达式,而且与哥尔斯坦函数k 相关。计算中利用Kramer 曲线作为螺旋桨效率的第一次近似,以利于初步估算螺旋桨的水动螺距角。升力线理论是建立在无粘流体基础上的,粘性的作用使扭矩增大、推力减小,可进行必要的螺距修正[4]。
根据近似法理论,对于切向诱导速度Ut有

式中:VA为螺旋桨进速;β 为螺旋桨进角。
在获得了水动螺距角分布tanβi以后,可以计算升长系数。
对于均匀水流中的螺旋桨,有

式中:l 为叶剖面弦长;D 为螺旋桨直径;Z 为桨叶数目;x 为无量纲化的径向坐标(即x=r/R);k 为哥尔斯坦函数;λ 为螺旋桨进速系数。
对于每片桨叶的无量纲环量分布,有

1.2 精确法
在精确法中,考虑由Z 个等距的空间螺旋线所诱导的速度分量。这些螺旋涡线是从螺旋桨叶片发出的螺旋涡片元体。因此由涡片所诱导的速度分量可以由从涡线的各个单元分量的积分而得,同时在一根涡线也能以诱导因子来表达。
对于切向和轴向诱导速度,有

式中:Ut为切向诱导速度;Ua为轴向诱导速度;VA为螺旋桨进速;xh为毂径比;和可以通过积分运算得出。
定义一个位移速度U*,它反映了螺旋桨进角β与水动螺距角βi之间的如下关系:

在均匀水流中的螺旋桨,环量G 的近似求解方程的离散形式可以写成

升长系数可以写成

2 螺旋桨设计算例
分别应用近似法与精确法进行最佳环量敞水螺旋桨设计。
2.1 最佳环量敞水螺旋桨设计(近似法)
用近似法进行最佳环量敞水(均匀水流)螺旋桨设计,相关设计参数如表1所示。得到的计算结果(水动力参数)如表2所示。
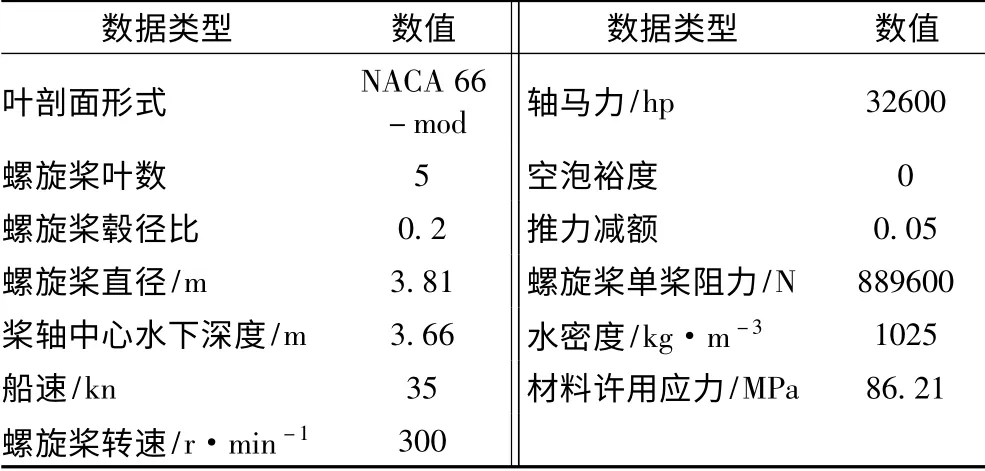
表1 近似法设计参数——螺旋桨参数Tab.1 Design parameters of Goldstein function method:propeller parameters
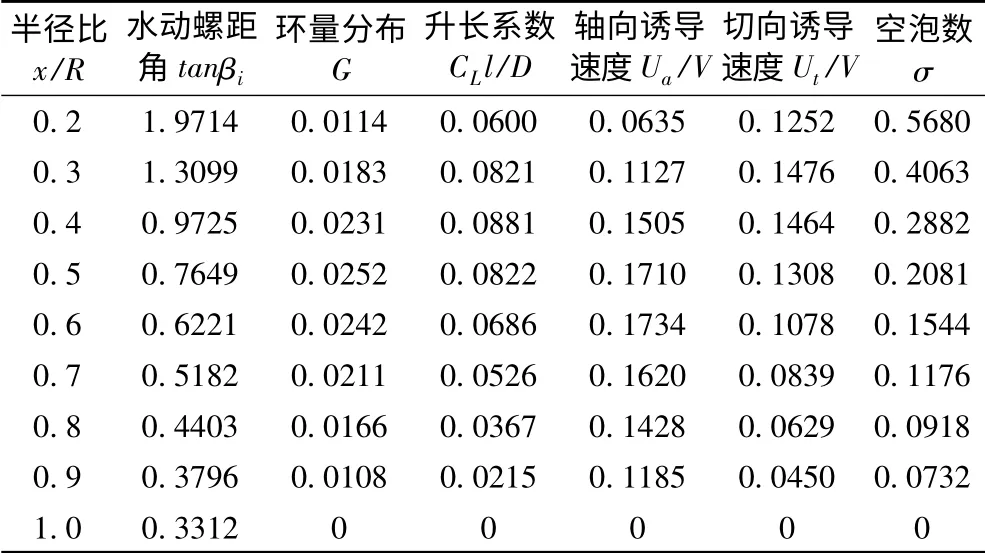
表2 近似法计算结果——水动力参数Tab.2 Hydrodynamic parameters calculated by Goldstein function method
2.2 最佳环量敞水螺旋桨设计(精确法)
用精确法进行最佳环量敞水(均匀水流)螺旋桨设计,相关设计参数如表3 ~表4所示。得到的计算结果(水动力参数)如表5所示。

表3 精确法设计参数——螺旋桨参数Tab.3 Design parameters of rigorous method:propeller parameters
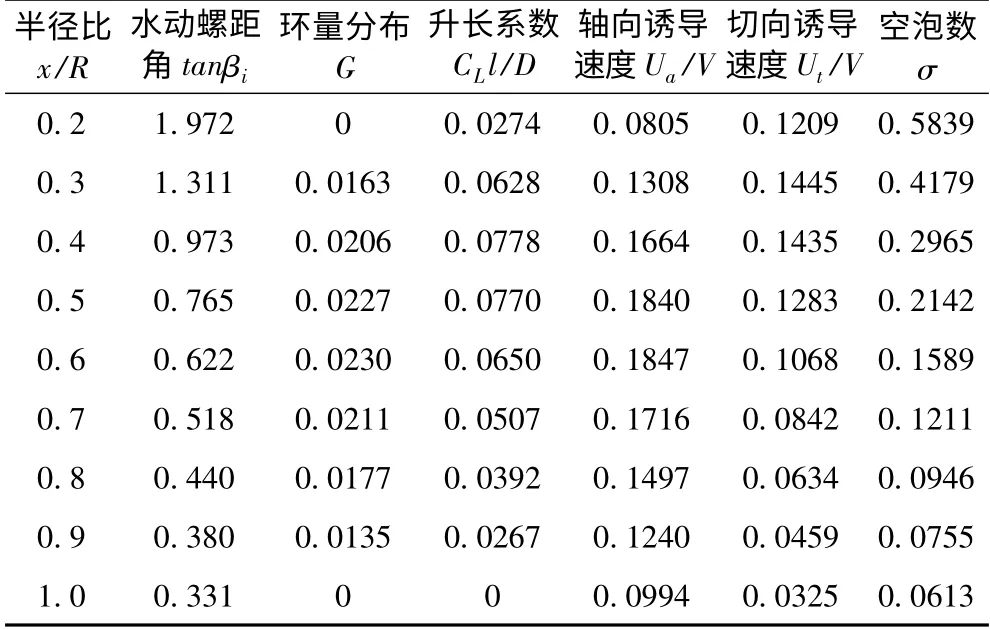
表5 精确法计算结果——水动力参数Tab.5 Hydrodynamic parameters calculated by rigorous method
3 近似法与精确法计算结果比较
对于最佳环量螺旋桨的设计,给定相同毂径比xh、进速系数λ、桨叶数Z、理想推力系数CTi和伴流分数ω 等设计要求,对于均匀水流(敞水)与适应伴流(船后),分别采用2 种不同的处理方法(近似法与精确法)进行计算,并比较分析。由于在设计过程中,2 种方法仅仅在计算环量G、轴向诱导速度Ua/V、切向诱导速度Ut/V和升长系数CLl/D 时有所差别,在计算得到各叶剖面的这4 个参数后,后续处理方法基本一致,因此此处仅对这4 个参数进行比较。
为了与近似法取得相同的初始设计条件,均匀水流螺旋桨的精确法设计中,需要给定一不随半径变化的位移速度U*(见式(6))。位移速度U*是直接影响水动螺距角分布、进而影响推力系数等性能参数的重要物理量。指定与近似法相似的水动螺距角分布形式
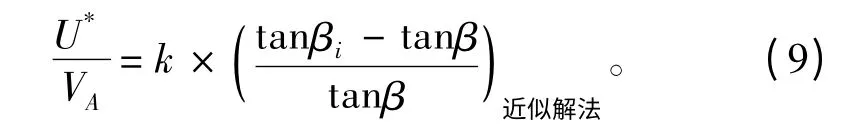
k 的取值由CTi决定:任意给定一k 值,然后进行螺旋桨设计计算,得到一相应的理想推力系数CTi。比较所得CTi与给定CTi,如果不同,则适当调整k,直到二者相等。
分别应用近似法与精确法在均匀水流(敞水)与适应伴流(船后)条件下进行最佳环量螺旋桨设计,计算得到的无因次环量、诱导速度和升长系数对比如图1 ~图6所示。
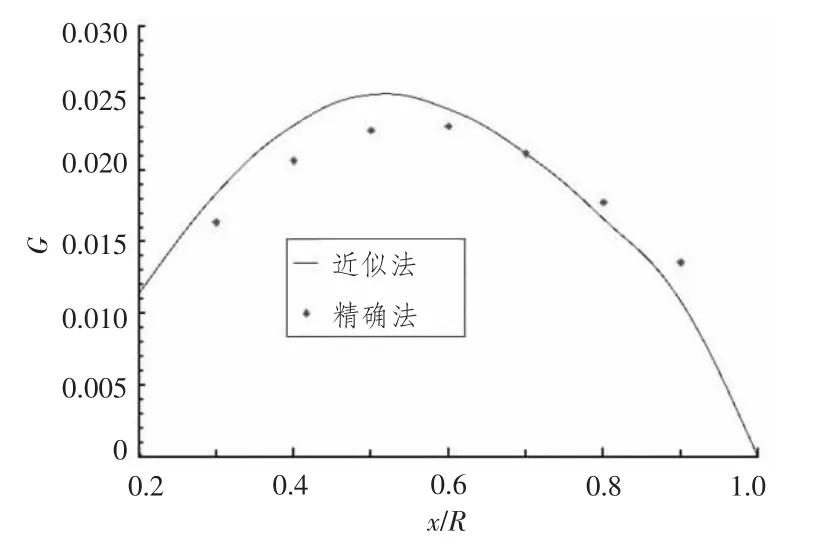
图1 均匀水流(敞水)螺旋桨近似法与精确法设计结果对比——无因次环量Fig.1 Propeller design results contrast of two methods underuniform wake(open water):dimensionless circulation
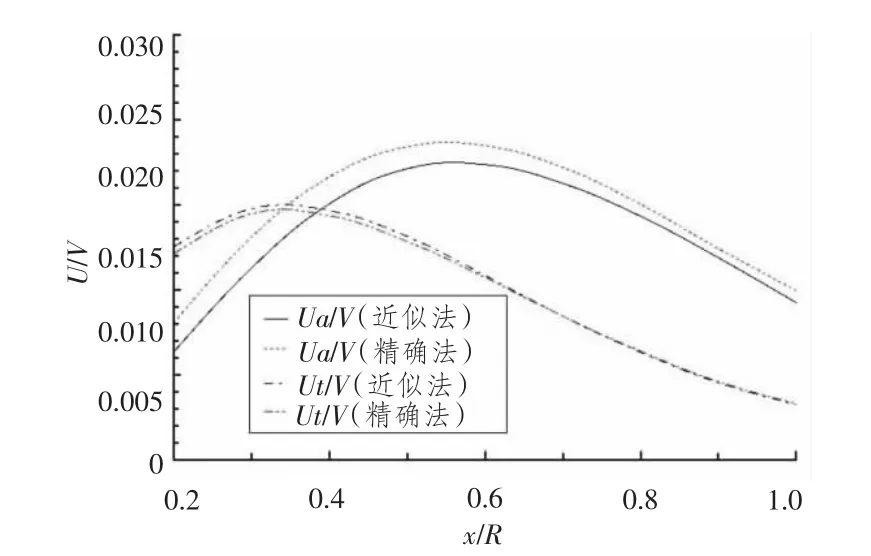
图2 均匀水流(敞水)螺旋桨近似法与精确法设计结果对比——诱导速度Fig.2 Propeller design results contrast of two methods under uniform wake(open water):induced velocity

图3 均匀水流(敞水)螺旋桨近似法与精确法设计结果对比——升长系数Fig.3 Propeller design results contrast of two methods under uniform wake(open water):lift coefficient

图4 适应伴流(船后)螺旋桨近似法与精确法设计结果对比——无因次环量Fig.4 Propeller design results contrast of two methods under non-uniform wake(after the ship):dimensionless circulation

图5 适应伴流(船后)螺旋桨近似法与精确法设计结果对比——诱导速度Fig.5 Propeller design results contrast of two methods under non-uniform wake(after the ship):induced velocity
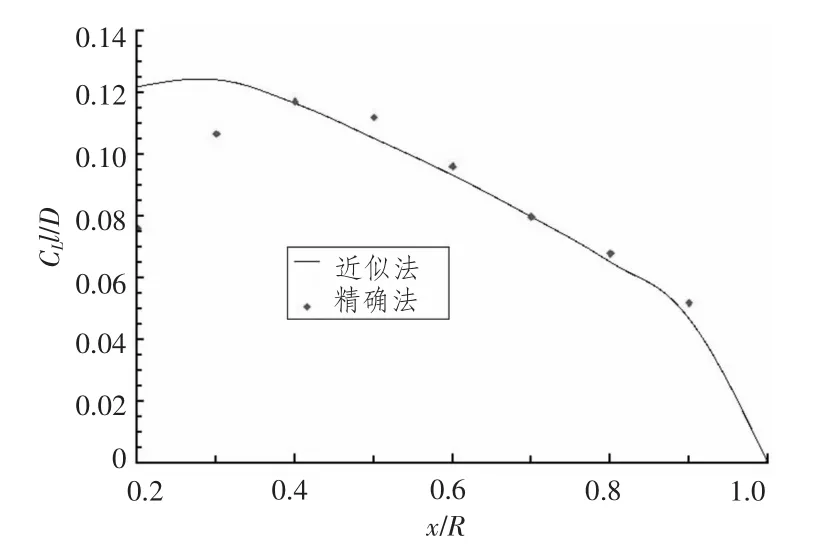
图6 适应伴流(船后)螺旋桨近似法与精确法设计结果对比——升长系数Fig.6 Propeller design results contrast of two methods under non-uniform wake(after the ship):lift coefficient
4 结 语
本文分别应用Morgan 关于近似法的理论与Lerbs 关于精确法的理论进行了螺旋桨理论设计。为了进行比较分析,提出了位移速度概念(U*),进而比较了2 种方法对应的环量分布、诱导速度和升长系数计算结果。通过对比可以看出,2 种方法的设计结果相当接近(特别是对于船后螺旋桨的水动力参数)。从而证实在实际进行螺旋桨设计时采用近似法进行初步估算可行。
[1]王言英.船用螺旋桨理论及其应用研究进展[J].大连理工大学学报,2006,46(2):306-312.
WANG Yan-ying.Technological advances in propeller propulsion of ships[J].Journal of Dalian University of Technology,2006,46(2):306-312.
[2]ECKHARDT M K,MORGAN W B.A Propeller design method[J].Trans SNAME,1968,76.
[3]LERBS H W.Moderately loaded propellers with a finite number of blades and an arbitrary distribution of circulation[J].Trans SNAME,1952,76.
[4]叶永兴.螺旋桨升力线理论在舰船设计及性能预报中的应用[J].舰船科学技术,1984(5):35-44.
YE Yong-xing.The application of propeller lifting line theory in ship′s design and performance prediction[J].Ship Science and Technology,1984(5):35-44.
[5]CARLTON J.Marine propellers and propulsion[M].Oxford:Butterworth Heinemann,2007.
[6]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,2005.

