纵横加肋圆柱壳稳定特性
王小明
(中国舰船研究设计中心,湖北 武汉430064)
0 引 言
圆柱壳结构具有力学性能好易于加工、耗材省的优点,广泛应用于海洋工程、船舶工程和水工建筑物。人们在设计圆柱壳结构时,一方面要保证其强度满足要求,另一方面还要保证其具有一定的稳定性。对于潜艇耐压壳来说,高强度材料的应用和潜艇大型化的发展,圆柱壳结构的稳定性往往显得更为重要。
环肋圆柱壳是指在圆柱壳内部或者外部加设环向肋骨的圆柱壳结构。对这类圆柱壳结构总体稳定性的讨论很多[1-7]。在讨论中,基本形成了共识:环肋圆柱壳总稳定性存在异常特性,异常特性产生的原因是环肋圆柱壳的纵向刚度不足。因此,要提高环肋圆柱壳总稳定理论临界压力必须提高圆柱壳结构的纵向刚度,可以增加板厚,也可以加设纵骨。后者充分利用材料,成为提高环肋圆柱壳稳定性临界压力的首选措施。这种横向设置环向肋骨、纵向加设纵骨的圆柱壳结构称之为纵横加肋圆柱壳。目前,对于纵横加肋圆柱壳总稳定性特性的讨论比较少,有必要对加设纵骨对环肋圆柱壳的稳定性影响进行研究。
1 环肋圆柱壳总稳定性的异常特性
环肋圆柱壳在各向均匀外压力作用下的总稳定理论临界压力公式如下[8]:
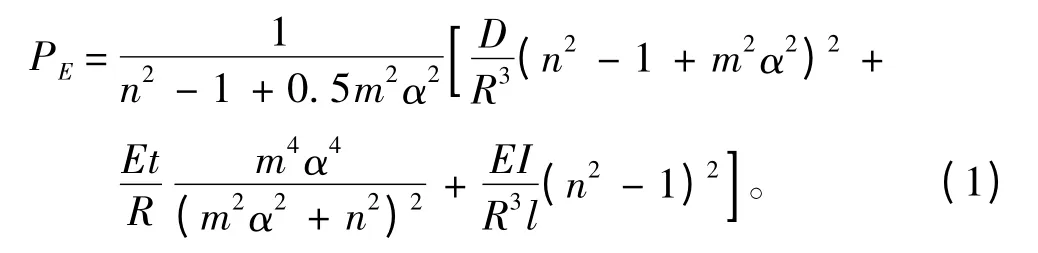
式中各字母所代表的含义可以参考文献[8]。
当环肋圆柱壳仅受纵向外压和仅受横向外压作用时,其总稳定理论临界压力和的计算公式[5]分别为:
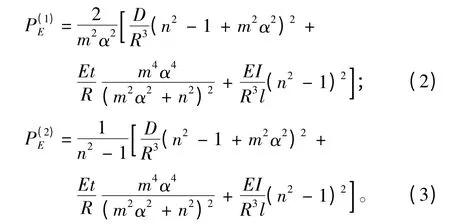
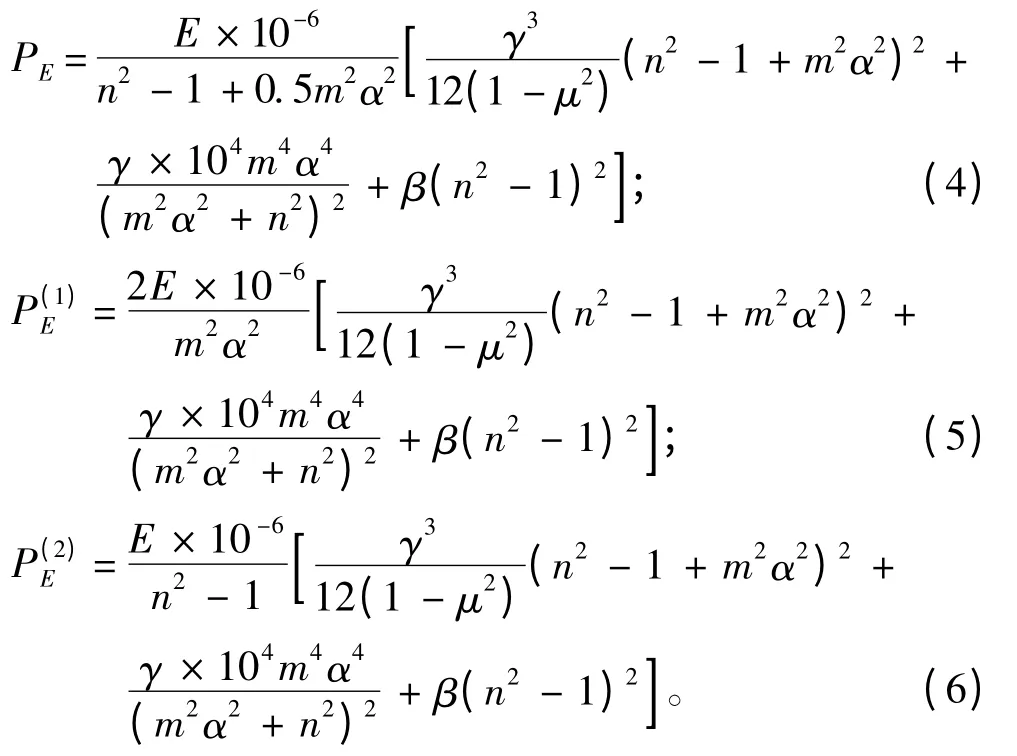
取β=3.0,γ=0.7[5],确定和随α 的变化规律,用编写的程序绘制和曲线,如图1所示。
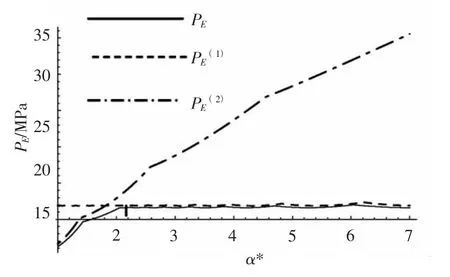
图1 PE-α 关系曲线Fig.1 PE-α relationship curves

图2 PE-β 关系曲线Fig.2 PE-β relationship curves
肋骨尺寸变化时,取α=2.5,γ=0.7[5],可以确定和随β 的变化规律,相应的PE和曲线如图2所示。
由图1和图2 可以看出,当α >α*或者β >β*时,增大α(减小舱长)或增大β(增大肋骨尺寸),环肋圆柱壳的总稳定理论临界压力几乎保持不变,这种特性即为环肋圆柱壳总稳定性的异常特性[1]。
对于图1,α >α*的区间称为异常特性区间Ⅰ;对于图2,β >β*的区间称之为异常特性区间Ⅱ。处在异常特性区间Ⅰ,Ⅱ的环肋圆柱壳,总稳定理论临界压力由纵向受压总稳定理论临界压力决定。要提高其总稳定临界压力,必须提高纵向刚度,以增加板厚亦可以加设纵骨。加设纵骨可以节省材料,发挥各个构件的优越性,成为首选。
2 纵横加肋圆柱壳总稳定性
2.1 纵横加肋圆柱壳总稳定性公式
纵横加肋圆柱壳的总稳定理论临界压力公式也可以类似式(1)的方法推导。实际上,仅需要在推导式(1)的过程中增加纵向肋骨的应变能即可[9]。每根纵向肋骨的应变能为:
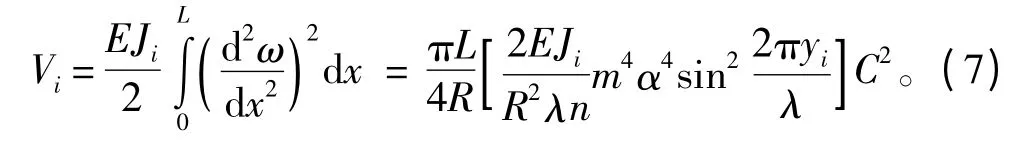
设圆周方向共加设N 根纵向肋骨,则纵向肋骨的总应变能为
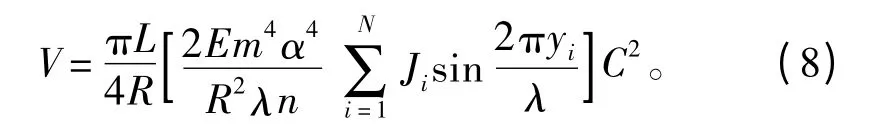
假设纵向肋骨等间距布置,截面尺寸相同,则Ji=J=常数。注意到纵向肋骨间距b=2πR/N,纵向肋骨之间的圆心夹角Δφ=2π/N,则b=Δφ·R。这样,式(8)可以表示为

式中i 为肋骨序数,i=1,2,3,…,N。当n·Δφ≠kπ,即n ≠kπR/b(k ∈N*)时,可以用三角公式证明。则
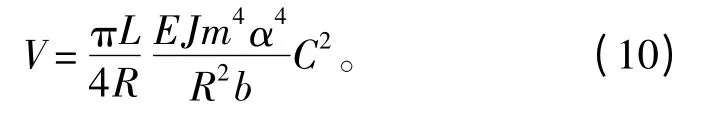
用类似于环肋圆柱壳总稳定理论临界压力公式的推导方法,可以得到纵横加肋圆柱壳总稳定理论临界压力公式

式中m,n 由相应于上式取得最小值条件确定。
2.2 纵向肋骨在总稳定性中的作用
用类似于推导式(2)和式(3)的方法,可以导出纵横加肋圆柱壳在仅受纵向外压作用下和在仅受横向外压作用下的总稳定理论临界压力公式。
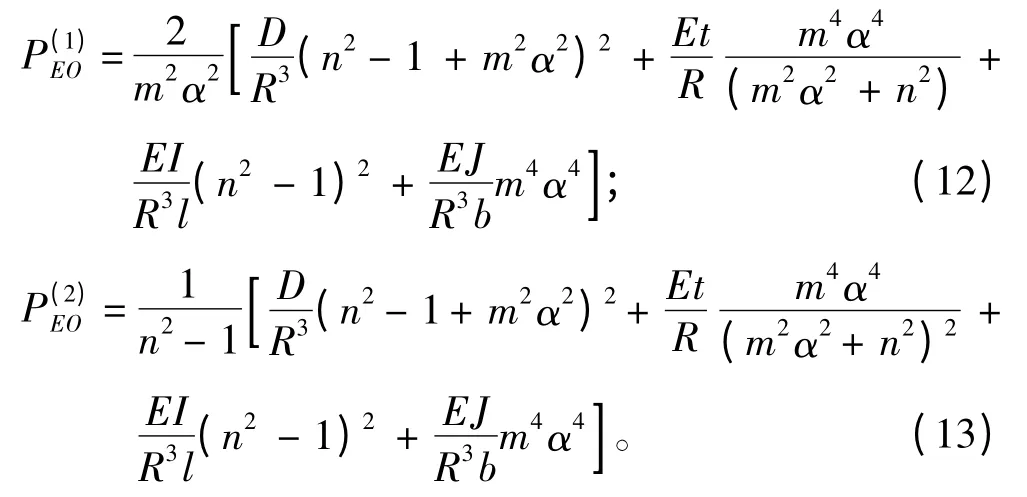
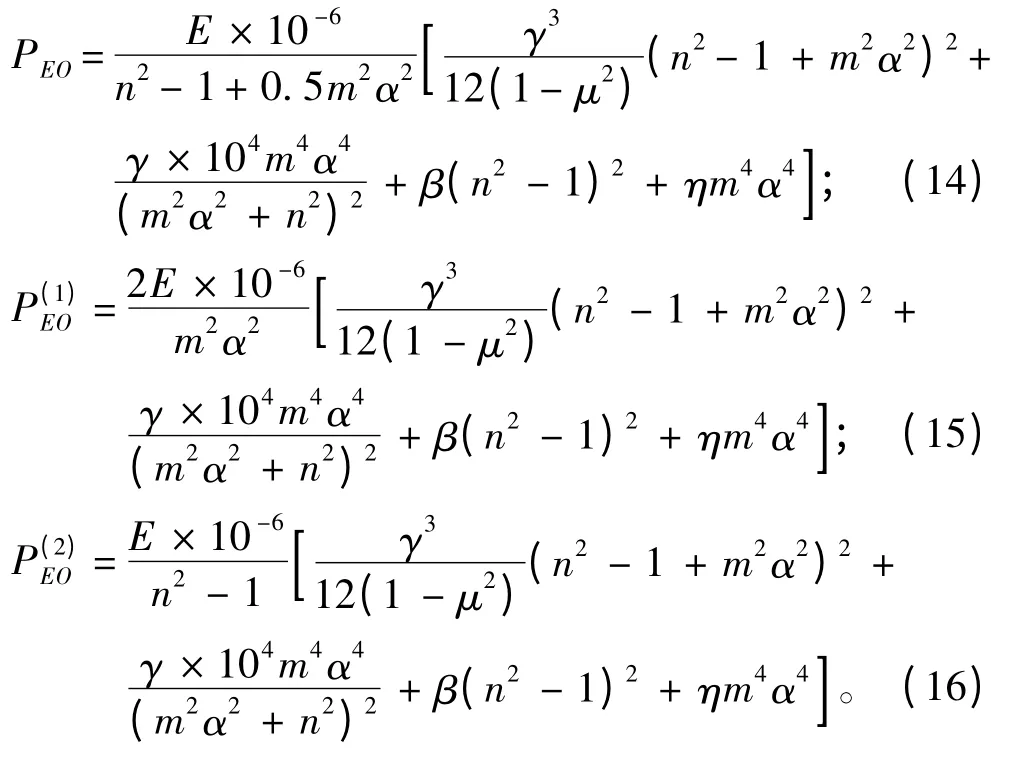

图3 PEO-η 关系曲线Fig.3 PEO-α relationship curves
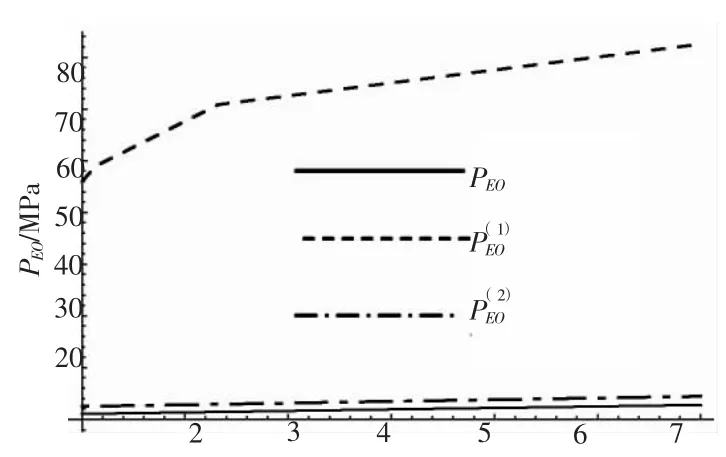
图4 PEO-η 关系曲线Fig.4 PEO-η relationship curves
当环肋圆柱壳处在正常特性区间时,加设纵骨。可以取α=1.5,β=3.0和α=2.5,β=2.0,绘出PEO-η 等3 条曲线,如图3和图4所示。
结合图1 ~图2 可以发现,α=1.5,β=3.0和α=2.5,β=2.0 都是处在环肋圆柱壳总稳定正常特性区间以内。从图3和图4 看出,这些区间内加设纵骨效果不明显,即总稳定理论临界压力增加不显著。
在环肋圆柱壳总稳定异常特性区间Ⅰ内加设纵骨,可以在图1 中取α=3.5,β=3.0和α=5.5,β=3.0,在这2 种条件下,纵骨对总稳定理论临界压力的影响区间如图5和图6所示。
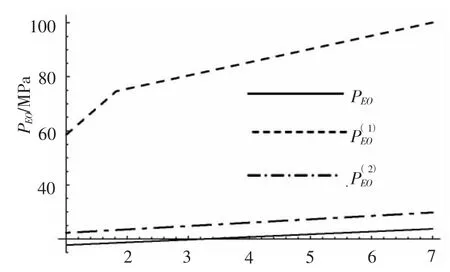
图5 PEO-η 关系曲线Fig.5 PEO-α relationship curves
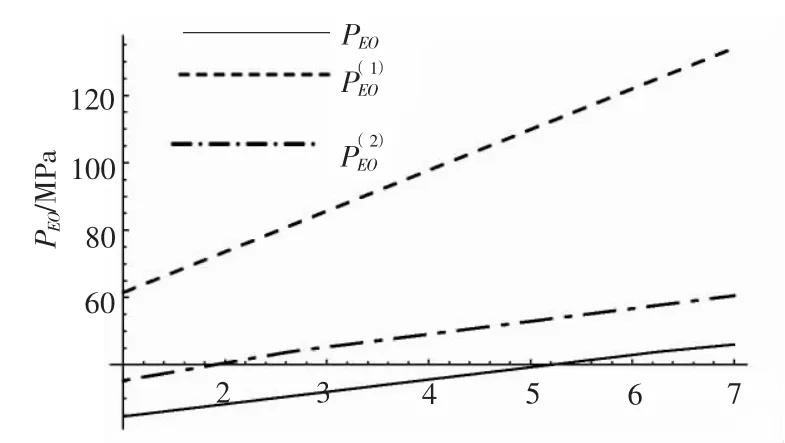
图6 PEO-η 关系曲线Fig.6 PEO-η relationship curves
图5和图6 反映的趋势是:在异常特性区间Ⅰ内,增加纵向肋骨可以提高总稳定临界压力,且α 越大(舱长越短),总稳定临界压力提高得越快。
考查环肋圆柱壳加设纵骨对总稳定临界压力的提高效果也要从图2 中选择异常特性区间点,取α=2.5,β=3.0和α=2.5,β=5.0。固定α,β,使η 变化,绘出这2 种情况下PEO-η 等3 条曲线,如图7和图8所示。

图7 PEO-η 关系曲线Fig.7 PEO-η relationship curves
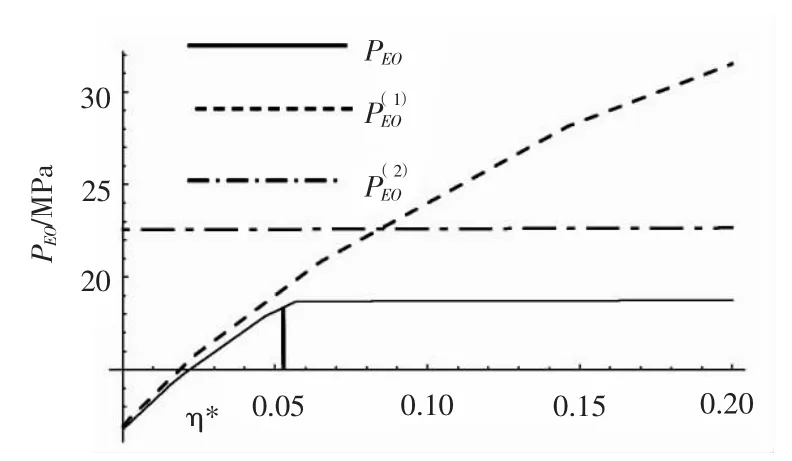
图8 PEO-η 关系曲线Fig.8 PEO-η relationship curves
图7和图8 共同反映了以下规律:在异常特性区间Ⅱ中,加设纵骨,环肋圆柱壳总稳定临界压力有所提高,且总稳定理论临界压力增长率较快仅发生在η值较小的一小段区间上。随后,总稳定理论临界压力几乎保持不变。这是因为在异常特性区间Ⅱ内,只需要增加少量的纵向刚度就可以使纵向受压临界压力大于横向受压临界压力,使得总稳定临界压力受制于横向受压临界压力。这时,η >η*区间内,增大纵骨尺寸,纵横加肋圆柱壳总稳定理论临界压力几乎不变,也是一类异常特性,这一区间称为异常特性区间Ⅲ。
3 相对厚度对加设纵骨效果的影响
以上讨论都基于相对厚度γ=0.7 所进行,随着潜艇耐压壳高强度材料的开发利用和潜艇大型化的需要,相对厚度γ 在逐渐减小。取γ=0.07,用同样的方法重新绘制图1和图2,重绘后的图形如图9和图10所示。

图9 PE-α 关系曲线Fig.9 PE-α relationship curves
当γ 减小后,异性特性区间扩大,因此第2 节所讨论的处在异常特性区间的点,现在依然处在异常特性区间内。将图5和图6 的相对厚度改成0.07,其余参数不变,重新绘制这2 个图形,如图11和图12所示。
再取异常特性区间Ⅱ内的点,取值与图7和图8 相同,即α=2.5,β=3.0和α=2.5,β=5.0,图13和图14 是相对厚度γ 改为0.07 后,上述2 种情况下的纵骨与总稳定理论临界压力的关系曲线。
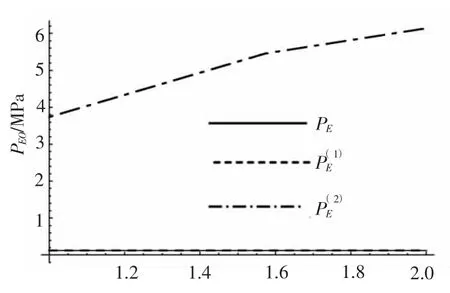
图10 PE-β 关系曲线Fig.10 PE-β relationship curves

图11 PEO-η 关系曲线Fig.11 PEO-η relationship curves
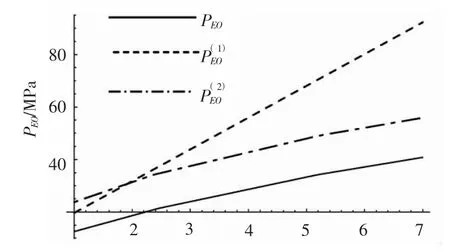
图12 PEO-η 关系曲线Fig.12 PEO-η relationship curves
将图11 ~图12 与图5 ~图6、图13 ~图14 与图7 ~图8 对比可以发现,相对厚度减小后,增加纵骨对总稳定理论临界压力的提高非常显著,即γ越小,加设纵骨的效果越明显。

图13 PEO-η 关系曲线Fig.13 PEO-η relationship curves
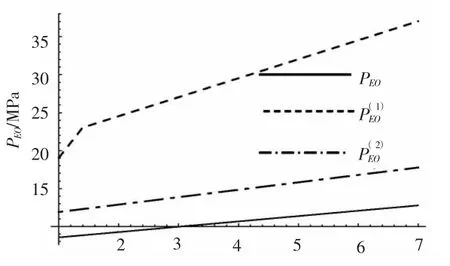
图14 PEO-η 关系曲线Fig.14 PEO-η relationship curves
4 结 语
环肋圆柱壳存在异常特性区间Ⅰ和异常特性区间Ⅱ,纵横加肋圆柱壳存在异常特性区间Ⅲ。出现前2类区间的原因是环肋圆柱壳的纵向刚度不足,后一类区间则是由于纵横加肋圆柱壳横向刚度不足所致。
在环肋圆柱壳的正常特性区间内加设纵骨不能提高总稳定临界压力。在异常特性区间Ⅰ内加设纵骨可以提高总稳定理论临界压力,且α 越大,理论临界压力提高得越快。在异常特性区间Ⅱ内增加纵骨,总稳定理论临界压力随纵骨尺寸增大出现先增大后保持不变,出现纵横加肋圆柱壳的异常特性区间Ⅲ,β 越大,异常特性区间Ⅲ就越小。
相对厚度γ 越小,用加设纵骨的办法来提高总稳定理论临界压力的效果越明显。
[1]谢祚水.环肋圆柱壳稳定特性研究[J].中国造船,1998(4):73-80.
[2]谢祚水,许辑平.潜艇薄壁大半径圆柱壳的总稳定性[J].中国造船,1994(2):82-88.
[3]武杰.环肋圆柱壳稳定性方程式特性探讨[J].中国造船,1995(1):45-53.
[4]王林,谢祚水.纵横加肋耐压圆柱壳结构稳定性[J].造船技术,1998(12):23-25.
[5]王晓天,姚文,梁超.不同纵横均匀外压作用下环肋圆柱壳稳定性分析[J].哈尔滨工程大学学报,2007(10):1079-1083.
[6]TATIANA V,PETER A.Buckling of circular cylindrical shells subject to uniform lateral pressure[J].Engineering structure,1996,18(8):604-614.
[7]ZOU R D,FOSTER C G.Simple solution for buckling of orthotropic circular cylindrical shells[J].Thin-Walled Structures,1995(22):143-158.
[8]许辑平.潜艇强度[M].北京:国防工业出版社,1980.
[9]谢祚水.受均匀外压力作用的圆柱壳结构形式的初步探讨[J].镇江船舶学院学报,1990,4(4):31-37.

