基于相干信号源的修正ISM算法

赵 曦，侯 朋，刘文帅

( 大连测控技术研究所，辽宁 大连116013)

0 引 言

1 宽带信号源模型

宽带信号相对于窄带信号来说，是指不满足窄带信号条件，与其中心频率相比具有很大带宽的信号。由于宽带信号的方向矢量与频率有关，所以宽带阵列信号可用频域模型表达为:

令:

写成宽带信号频域模型可表示为:

由式(2)可知，宽带信号源模型是与方向矩阵和频率有关的频域模型。

2 非相干子空间算法

非相干子空间算法(ISM)是最早出现的宽带DOA 估计算法，这种算法的基本思想是将宽带信号在不重叠的频域上分解为若干个子带，每个子带可以看作一个窄带信号分量，然后在每个子带上直接进行窄带处理，最后对所有子带的空间方位谱进行加权平均，得到宽带信号的DOA 估计。本文采用常规波束形成算法、MVDR 波束形成算法、MUSIC算法来进行窄带处理。

首先将观察时间T0内采集的信号分为K个子段，则每段时间长度为Tk=T0/K。然后对每段信号做J 点的离散傅立叶变换(DFT)得到K 组互不相关的窄带频域分量(K 为频域快拍)，由此得到K个快拍，记为Xk(fj)， (j=1，2…J;k=1，2，…K)。ISM的目的就是由这K个频域快拍估计多个目标的方位。接收信号各频率点输出为:

式中:Xk(fj)，Sk(fj)，Nk(fj)分别为某频率点的接收数据。信号噪声的DFT 变换，A(fj，θ)为方向矢量矩阵。接收信号在频率fj上的协方差矩阵:

湖北省汽车零部件产业转型升级的关键在于提升技术水平和提高产品研发能力，应紧跟汽车零部件产业技术前沿，按照“归类聚合、高新准入、短板先行、扩大规模”的指导思想，加快设备技术和企业管理的改造升级，通过存量升级提高自主技术创新能力，通过增量升级发展产业集群。

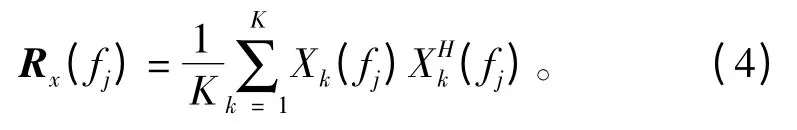
对协方差矩阵Rx(fj)进行特征值分解:

可以求出对应的信号子空间Es(fj)与噪声子空间En(fj)。

利用窄带信号CBF算法、MVDR算法、MUSIC算法在频率fj点上的方位谱:

再对J个频带得到的空间方位谱平均，即可得到ISM－CBF、ISM－MVDR、ISM－MUSIC 空间谱:

该方位谱出现峰值的方位即为信号方位估计值。

3 修正的非相干子空间算法

ISM算法是将宽带信号在频域上分解为若干个窄带分量，然后直接对每个窄带分量进行方位谱估计，这种算法能解决非相干信号源的DOA 估计问题，但对于相干信号源没有很好的分辨能力。在这里引入修正非相干子空间算法(MISM)［3］，通过对接收矩阵的去相关运算处理，实际上是一种空间平滑处理，使ISM算法可以扩展到宽带信号相干源DOA 估计中。具体算法如下:

首先对接收数据阵进行共轭重建，令

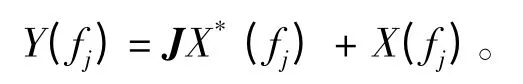
由此可见，在每一频率fj上使用新的协方差矩阵构造CBF，MVDR，MUSIC算法的空间方位谱，对所有子带的空间方位谱进行平均，可得到宽带信号的空间方位谱估计。

式中En(fj)为协方差矩阵R(fj)进行特征值分解所对应的噪声子空间。

对接收矩阵的共轭重建实际上是一种前后项空间平滑的处理方法，但实际上这里仅仅使用一个子阵，即子阵和原阵是完全一样且阵元数也相同，因此该方法不会损失阵列孔径。空间平滑处理消除了因相干信号存在而导致的基阵协方差矩阵的奇异性问题，从而解决了处理相干信号源的方位估计问题。

4 仿真实验分析

仿真条件:假设信号为宽带信号，阵元数为12，阵元间隔d=λ/2 ，采样频率fs=4f0，中心频率f0=1 500 Hz，基阵的工作频率带［fl，fh］=［f0/2，f0］。在频带［fl，fh］上有均匀频谱。背景噪声为与信号不相关的同频带高斯白噪声。

1)仿真实验一

要求采用ISM－ CBF、ISM－ MVDR、ISM－MUSIC 三种方法估计2个信号源的方位，改变入射信号的相干性，并讨论分析方法的性能。

①入射角－5°=［－5°，15°］，假设2个信号源为非相干信号，如图1所示。假设2个信号源为相干信号，如图2所示。

②入射角－2°=［－2° 2°］，假设2个信号源为非相干信号，如图3所示。假设2个信号源为相干信号，如图4所示。

图1 θ=［－5°，15°］非相干信号的ISMFig.1 ISM for incoherent signal (θ=－5°，15°)

图2 θ=［－5°，15°］相干信号的ISMFig.2 ISM for coherent signal (θ=－5°，15°)

图3 θ=［－2°，2°］非相干信号的ISMFig.3 ISM for incoherent signal (θ=－2°，2°)

图4 θ=［－2°，2°］相干信号的ISMFig.4 ISM for coherent signal (θ=－2°，2°)

图1和图3 显示了对应3 种方位估计的结果。从图中可以看出，当其他条件不变，减小2个非相关信号源入射方位间隔，常规波束扫描已无法分辨2个信号的方位，说明ISM－CBF 常规波束扫描方法对2个信号源的方位分辨力差，ISM－MVDR 波束扫描方法居中，ISM－MUSIC 方法具有最高的方位分辨力，它最小可分辨方位夹角小于CBF的1/3。

图1和图3 表示信号源为2个非相干的信号源;图2和图4 表示信号源为2个相干的信号源。当入射方位间隔比较大时，无论2个信号源时相干还是非相干，都能分辨出方位角度。但是当信号源是相干时，运用ISM 方法(见图1)，明显比图2 分辨能力好，抑制干扰噪声的能力强。当入射方位间隔减小，2个相干信号源已经无法分辨出入射角方位，分辨分辨能力严重下降。说明ISM 方法主要基于信号源非相干。

2)仿真实验二

假设2个信号源为相干信号，SNR=［15，15］，要求 采 用MISM－ CBF、MISM－ MVDR、MISM－MUSIC 三种方法估计2个信号源的方位，并且与入射信号为非相干信号的ISM算法进行对比分析。其他仿真条件与仿真实验一相同，如图5～图8所示。

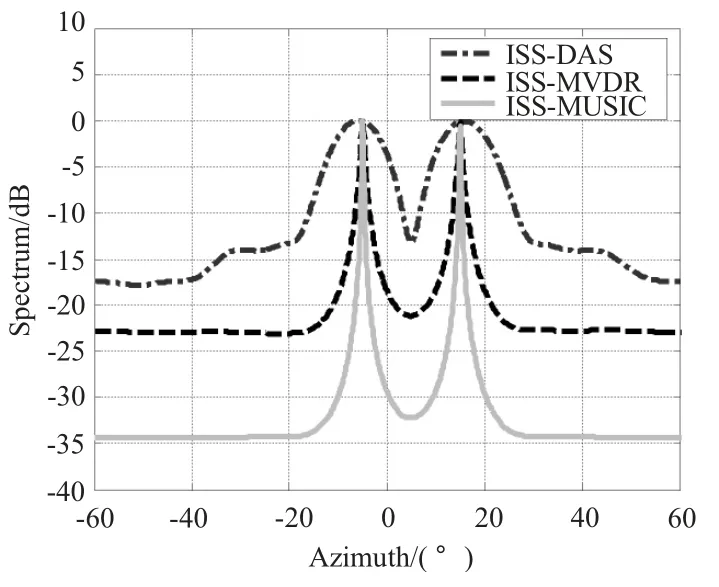
图5 θ=［－5°，15°］相干信号的MISMFig.5 MISM for coherent signal (θ=－5°，15°)

图6 θ=［－5°，15°］相干信号的ISMFig.6 ISM for coherent signal (θ=－5°，15°)

图7 θ=［－1°，4°］相干信号的MISMFig.7 MISM for coherent signal (θ=－1°，4°)

图8 θ=［－1°，4°］相干信号的ISMFig.8 ISM for coherent signal (θ=－1°，4°)

图5和图7 显示了对应3 种方位估计的结果。可以看出，当其他条件不变，减小2个相干信号源入射方位间隔，常规波束扫描已无法分辨2个信号的方位，说明MISM－CBF 常规波束扫描方法对2个信号源的方位分辨力差，MISM－MVDR 波束扫描方法居中，MISM－MUSIC 方法具有最高的方位分辨力，这与ISM算法结果相同。

图5和图6 表示信号源为2个相干的信号源，当入射方位间隔比较大时，都能分辨出方位角度。但运用如图5所示的MISM 方法，明显比图6 分辨能力好，抑制干扰噪声的能力强。当入射方位间隔减小，如图7和图8所示，相干信号的ISM 已经无法分辨出入射角方位，分辨分辨能力严重下降。而运用MISM 方法的相干信号，除了MISM－CBF 外其它2 种算法依然能够清晰的分辨出角度。说明修正的ISM算法能够解相干信号源，并且具有较窄的主瓣宽度和较低的旁瓣。这同时也说明了CBF算法对非相干信号源的分辨能力好于相干信号源。

5 结 语

本文介绍的基于相干信号源修正ISM的算法(MISM)，确实能解决入射为相干信号源问题，并且能获得较窄的主瓣宽度较低的旁瓣，验证了算法的有效性。通过仿真比较基于CBF、MVDR和MUSIC的ISM算法和MISM算法，可以得出MUSIC算法的分辨力和抑制噪声的能力最强，MVDR算法其次，CBF算法所反映出的能力最差。其中，CBF算法对非相干信号源的敏感度好于相干信号源。在后续的学习中将进一步通过外场实验验证算法的有效能力。

［1］VACCARO R J.The past，present and the future of underwater acoustic signal processingm［J］.IEEE Signal Processing Magazine，1998，15(4):21－51.

［2］WAX M，SHAH T，KAILATH T.Spatio-temporal spectral analysis by eigenstructure methods［J］.IEEE Trans.ASSP，Aug 1984，32:817－827.

［3］KUNDA D，Modified MUSIC algorithm for estimating DOA of signal［J］.Signal Processing，1996，48(1):85－90.

［4］CAPON J.High-resolution frequency-wavenumber spectrum analysis［J］.Proc of IEEE，1969，57(8):1408－1418.

［5］HIRAKAWA M，TSUJI H，SANO A.Computationally efficient DOA estimation based on linear prediction with Caponmethod.2001 IEEE International Conference on ASSP，Salt Lake City，UT，USA，2001(5):3009－3012.

［6］SCHMIDT R O.Multiple emitter location and signal parameter estimation［J］.IEEE Trans，1986，34(3):276－280.