基于时间扩展UML活动图的工作流过程建模方法

蔡 敏，卢 佩

（杭州电子科技大学 管理学院 工业工程与管理研究所，浙江 杭州 310018）

0 引言

工作流模型是对企业业务流程的详细描述，工作流强调企业业务流程的自动化。随着我国信息化的快速发展，工作流管理系统的应用越来越普遍，企业对其依赖越来越大，传统的工作流系统已经不能满足现在企业高效率的要求。提高效率最有效的办法，就是缩短产品生命周期，精炼企业业务流程，减少各个环节的处理时间，对时间进行有效全面地管理。

1 国内外研究现状分析

随着企业的不断发展，业务流程愈来愈复杂。以简单的建模方法将企业复杂工作流进行全面的建模，是企业一直以来的追求。工作流模型的核心是工作流过程模型，目前比较成熟的工作流过程建模方法主要有两种：①基于工作流图的建模方法，优点是比较适合建立复杂的业务流程，缺点是模型元素太多，建立的模型过于复杂，不易懂，对时间因素的考虑不太成熟；②基于Petri网的建模方法，优点是模型有现成的软件可以对其进行仿真优化，当然也有很多学者对Petri网进行了时间元素的研究，缺点是比较古板，不容易继承和扩展［1］。

目前国内外有许多学者都从事工作流系统的建模和研究。李宣东等给出了统一建模语言（Unified Modeling Language，UML）活动图的语义形式描述，并在此基础上提出了实时UML 活动图的语义描述，但他们考虑的时间因素相对比较简单［1］。然而企业的流程是复杂的，在运行过程中所遇到的时间因素也是形形色色的。文献［2］主要分析了用UML活动图建立工作流过程中各种模式的优势，并给予验证，同时指出UML活动图相比Petri网建模的优点，最后也给出了UML 活动图建模方面的不足：①缺少精确的语法和语义；②不能完整体现几种重要的活动之间的同步操作。文献［3］假设活动过程中不浪费时间，对UML 活动图的实时执行性进行了语义描述，这些语义都是基于状态图表形式进行的，但是对活动进行过程、活动转移过程而言，时间关系到企业生产、运营效率，是很要的因素。文献［4］主要对UML建模语言和Petri网建模语言进行了对比，指出UML对于工作流建模的优势，最后给出了Petri网到UML 的映射，完成了Petri网与UML建模的完美融合，但并没有涉及时间因素的处理。文献［5］和本文研究的相关度比较大，都是基于时间约束的UML 活动图的研究，不同之处在于文献［5］通过使用timedCSP 方法，对活动中的STOP／WAIT／SKIP等状态进行了语义形式的描述与时间限制，并给出了语义描述，但是没有考虑影响这些状态的时间因素，同时文献［5］只考虑了活动状态的时间约束，其实在活动转移的过程中也存在时间约束，例如产品设计完成后要进行设计的审阅，即从设计完成到设计审阅活动的转移过程可能会出现系统故障，即这个转移过程会延长，也就是活动的转移需要给予时间范围的约束。文献［6］提出建立和描述工作流应用的一套UML活动图的逐步精炼技术，并详细介绍了其精炼模式，最后提供实例证明了精炼模式的正确性。文献［7］指出在具有科学性的工作流中，对偶发性短暂性危害预防与阻止的重要性，并指出在优化或预防这种偶发性、短暂性危害流程中所面对的两个重要的基本问题。在此基础上提出一种新颖的算法，并通过最后的仿真实验验证了算法的正确性。

通过以上现状的分析可知，目前基于UML 活动图对工作流过程的建模有以下优点：①UML 活动图具有抽象性和用户友好性标识，业务专家和系统分析师都能很好地理解该模型；②可扩展性机制针对不同问题可进行柔性变通；③在业务建模和软件工程水平上的可应用性，有效地减少了业务建模工作者和软件工程师之间的代沟。当然UML活动图建模也有其不足之处，例如：①缺乏精确的语法语义，容易导致模糊性和模型死锁等问题；②UML 活动图在时间约束上缺乏有效的约束，目前仅存在于等待状态和活动状态；③UML 活动图在其流程模式上缺乏有效的研究。

本文针对UML 活动图所存在的第二个不足进行了研究，主要不同在于：①在考虑活动状态所具有的时间因素的同时，也考虑了活动转移的时间约束；②针对活动和转移的时间约束，考虑影响时间的6种因素（活动中资源到来时间、资源有效时间、活动延迟时间、跃迁有效时间、跃迁延迟时间、活动截止时间），通过语义形式进行了描述，并计算出活动最早开始时间、最晚开始时间、最早结束时间、最晚结束时间，跃迁的最早开始时间、最晚开始时间、最早结束时间、最晚结束时间，在时间上加强了活动与转移之间的紧密型；③除了对6种路由进行时间扩展外，还提出基于等待状态事件触发活动转移路由，解决了循环活动事件时间计算的问题。

基于以上理论研究，本文提出基于时间扩展的UML活动图的工作流模型，在语义描述的基础上，不仅有效解决了UML 活动图的模糊性，防止了流程死锁的发生，还对工作流程中的时间进行了全面控制与管理，以有效缩短产品上市周期，提高企业生产和运营效率。

2 基于时间扩展的UML活动图工作流过程语义描述

2.1 工作流与UML活动图的语义映射

UML活动图描述活动之间的顺序，展现从一个活动到另外一个活动的控制流，能够表现动作是怎样发生的、动作要干什么、动作是在何处发生等，因此使用UML活动图能够很好地对工作流进行描述。工作流概念模型到UML活动图之间的具体映射如下：

（1）用动作状态、活动状态表述工作流中的活动（任务）。

（2）用UML活动图中的初始状态、终止状态表示工作流过程中的开始节点和结束节点。

（3）用UML 活动图中的控制流表示活动之间的转移，即工作流模型中的控制流。

（4）用UML 活动图中的分叉或结合元素表示工作流模型中的同步元素。

（5）用UML 活动图中的分支或合并元素表示工作流模型中的选择元素。

（6）用UML 活动图中的对象节点表示工作流模型中的各种数据信息。

（7）用UML 活动图中的泳道元素表示工作流模型中的人员、角色、部门、职务元素。

（8）用UML 活动图中的对象流表示工作流模型中的资源流和数据流。

（9）用UML 活动图中的注释表示工作流模型中的标注元素。

通过以上UML活动图元素和工作流元素之间的完整映射，全面真切地描述工作流的各种属性和状态。

过程决定了案例的生命周期，被称为案例的“路由”。路由结构又称为工作流模式。工作流是通过控制流将各种活动按照一定的次序串接而成的，工作流模式则是反映工作流中控制流的一般特征，是从控制流中提取出来的、具有某种普遍特征的控制流片段。

工作流的6种路由与UML活动图路由的映射如下：

（1）顺序路由 描述活动发生的先后顺序，如图1所示。

（2）循环路由 描述活动的循环结构，如图2所示。

（3）与分支 活动完成后，其他活动可任意或者同时执行，如图3所示。

（4）与结合 描述几个活动完成后转移到下一个活动，如图4所示。

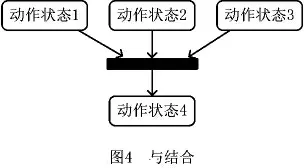
（5）或分支 分为带条件和不带条件的或分支路由，描述了活动在条件的约束下可以执行之后活动中的某一个，如图5所示。

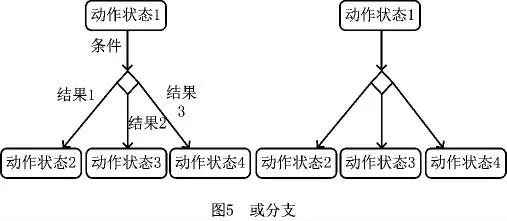
（6）或合并 分为带条件和不带条件的路由，描述了几个活动中条件为真的活动执行完成后转移到下一个活动的执行，如图6所示。

2.2 UML活动图语义描述

下面介绍UML活动图的形式语义。跃迁是从一种状态向另一种状态的流动。

定义1M和N是自然数集合，活动图D是一个多元组，D=（A，T，F，a1，aF）。其中：A=｛a1，a2，a3，a4，…，am｝是一个有限活动状态集；T=｛t1，t2，t3，t4，…，tn｝是一个有限完成跃迁集；F⊆（A×T）∪（T×A）是流关系；a1∈A是初始活动状态，aF∈A是终止活动状态。

只有一个跃迁t满足（a1，t′）∈F；对于任何t′∈T，（a1，t′）∉F且（aF，t′）∉F。

定义2D=（A，T，F，a1，aF）是一个活动图。D中的当前状态μ是A中的任意子集。对于任意跃迁，t∈T，＊t=｛a∈A｜（a，t）∈F｝和t＊=｛a∈A｜（t，a）∈F｝分别表示t的前提和后提。如果＊t⊆μ，则跃迁t对于状态集μ中是可触发的，否则是不可触发的。用enabled（μ）表示μ中可触发的跃迁集。

在某时刻，可触发的跃迁必须满足定义3所描述的两个条件。

定义3D=（A，T，F，a1，aF）是一个活动图。跃迁t∈T能从状态μ触发，当且仅当：

（1）t∈enabled（μ）；

（2）（μ-＊t）∩t＊=∅。

新状态μ′=（μ-＊t）∪t＊。

定义4D=（A，T，F，a1，aF）是一个活动图，D的一个运行σ是一个状态和跃迁的序列，

其中：μ0=｛a1｝，μn=｛aF｝；ti∈enabled（μt），i≥0；μi=（μi+1-＊ti-1）Yt＊i-1，i≥1。

2.3 时间扩展的UML活动图语义扩展

在以上叙述的基础上加入全面时间因素，形成基于时间的UML 活动图，扩展后的时间UML 活动图语义定义如下［8］：

定义5 改进

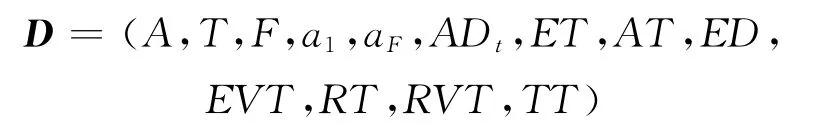
是一个13元组的活动图。

其中：

A=｛a1，a2，a3，a4，…，am｝是一个有限活动状态集。

T=｛t1，t2，t3，t4，…，tn｝是一个 有限完成跃迁集。

F⊆（A×T）∪（T×A）是流关系。

a1∈A是初始活动状态。

aF∈A是终止活动状态。

只有一个跃迁t满足（a1，t′）∈F；对于任何t′∈T，（a1，t′）∉F且（aF，t′）∉F，D=（A，T，F，a1，aF）构成一个活动图。

AD表示活动的延迟时间，一般活动的延迟时间都是取某个范围的值，记作AD=［c，d］，表示活动因某种外在因素导致活动执行时间延长。

ET表示跃迁的最早触发时间、最晚触发时间、最早结束时间、最晚结束时间的集合，记作ETt=｛EFTt，ELTt，EFFt，ELFt｝。

AT表示活动的最早开始时间、最晚开始时间、最早完成时间、最晚完成时间的集合，记作ATt=｛AFTt，ALTt，AFFt，ALFt｝。

ED表示跃迁的触发延迟时间，记作［a，b］，指跃迁经过EDt的延时时间才能触发t＊。

EVT表示跃迁有效时间，通常取值为某个范围，记作［e，f］（e和f为时间点，且0＜e＜f），设资源的到达时间为t，则该资源只在时间区间［e+t，f+t］上可用。

RT表示资源到达活动的时间。

RVT表示资源的有效时间，通常取值为某个范围，记作［g，h］（g和h为时间点，且0＜g＜h），设某个跃迁的达到时间即使能时间为t，则该跃迁只在时间区间［g+t，h+t］上可以触发。

TT表示整个活动流程的时限约束，如无此约束，则用-1表示。

定 义6D=（A，T，F，a1，aF，ADt，ET，AT，ED，EVT，RT，RVT，TT）是一个时间活动图。对于任意活动a∈＊t，活动的延迟时间为［c，d］，跃迁t∈T的有效触发时间为EVT（t）=［e，f］，经过EDt后，能从状态μ触发，当且仅当：

（1）t∈enabled（μ）；

（2）（μ-＊t）∩t＊=∅；

（3）对于任意的a∈＊t，EFT（a）≤Et+c+e；对于任意的a′∈μ，Et+d+f≤ELTt。

定 义7D=（A，T，F，a1，aF，ADt，ET，AT，ED，EVT，RT，RVT，TT）是一个基于时间的活动图。D的一次运行σ是一个状态、跃迁、跃迁延时时间、跃迁最早触发时间和跃迁最晚触发时间的序列，

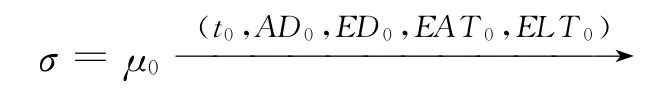
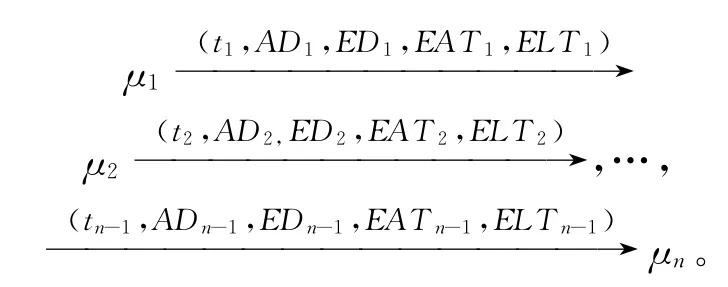
用delay（σ）表示运行σ的所有延时之和，即

其中：μ0=｛a1｝为初始状态，μn=｛aF｝为终止状态；对于任意的i（1≤i≤n），μi由μi-1 经过EDi-1+ADi-1延时后触发ti-1得到。

定 义8D=（A，T，F，a1，aF，ADt，ET，AT，ED，EVT，RT，RVT，TT）是一个基于时间扩展的活动图。如果对于任意活动a∈＊t存在事件的触发，则活动的最早开始时间与所有资源最大到达时间、资源有效时间、活动延迟时间有关。设活动a∈＊t，每一个资源到达时间为RT（ri），有效时间RVT（ri）=［gi，hi］，则活动的最早开始时间

如果活动a∈＊t不存在事件触发RT（ri）=0，RVT（ri）=［0，0］，则活动的最早开始时间AFT（a）=0。

定 义9D=（A，T，F，a1，aF，ADt，ET，AT，ED，EVT，RT，RVT，TT）是一个基于时间扩展的活动图，同理定义8活动a∈＊t的最晚开始时间

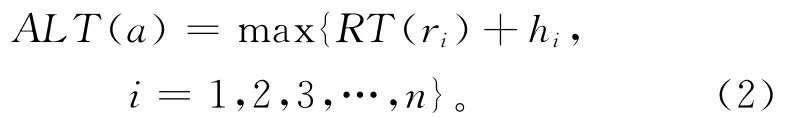
定义10 活动图跃迁t的事件e的使能时间Et，由跃迁输入的所有资源的最晚到达时间、有效时间和活动延迟时间确定，设跃迁t有n个输入资源，每一个资源的到达时间为RT（ri），有效时间RVT（ri）=［gi，hi］，活动延迟时间为［c，d］，则活动的最早完成时间

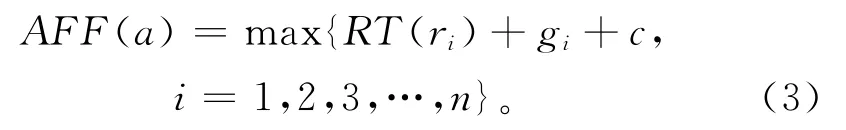
定义11D=（A，T，F，a1，aF，ADt，ET，AT，ED，EVT，RT，RVT，TT）是基于时间的活动图，同理定义8，活动的最晚完成时间

定义12 如果活动a的最晚完成时间大于截至期限TT（a），则活动的最晚完成时间ALF（a）=TT（a）；如果活动a+1的最早开始时间小于活动a的最晚完成时间，则AFT（a+1）=max｛ALF（a），AFT（a+1）｝。

定义13 跃迁t的事件e的最早触发时间EFTa由活动a的最晚完成时间和有效时间决定，设跃迁的使能时间为Et，跃迁t的有效时间为EVT（t）=［e，f］，则

定义14 跃迁t的事件e的最迟触发时间ELTt由以下几个时间因素决定：活动a的输入资源的到达时间、活动a的输入资源的有效时间、跃迁t的有效时间、活动的延迟时间、活动的最晚完成时间、跃迁t的触发延迟时间、整个流程的时限约束。

设活动a有n个输入资源，每个资源的到达时间为RT（ri），每个资源的有效时间为RVT（ri）=［gi，hi］，活动的最晚完成时间为ALF（a），跃迁t的触发延迟时间为［a，b］，跃迁t的有效时间为EVT（t）=［e，f］，活动延迟时间为［c，d］，整个活动流程的时限约束TT为m，则

定义15 跃迁t的事件e的最早完成时间由跃迁t的最早触发时间和跃迁的延时时间两个因素确定。设跃迁t的延迟时间为［a，b］，跃迁的最早触发时间为EFTt，则跃迁最早完成时间

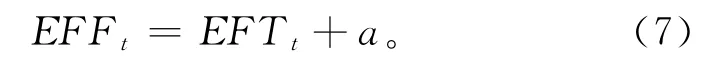
定义16 跃迁t的事件e的最晚完成时间由跃迁t的最晚触发时间和跃迁t的延时时间两个因素确定。设跃迁t的延迟时间为［a，b］，跃迁t的最晚触发时间为ELTt，则跃迁最晚完成时间

2.4 路由结构扩展

前文对工作流建模的6种路由结构［9］进行了分析，在此基础上加入基于等待状态的事件触发路由结构，如图7所示。本文的对象流状态有两种含义：①表示参与活动1的角色，这种类型的对象流方向只有由对象流状态指向活动1一种。②表示活动1所需的对象数据，这种对象流数据有两种流向。如果流向由对象流状态指向活动1，则表示活动1在执行时所需的数据信息；如果流向由活动1指向对象流状态，则表示活动1在执行过程中所产生的数据信息是要永久保存的数据。活动1执行完后进入等待状态，在事件2的触发下等待状态跃迁到活动2，这时时间约束位于控制流的上部，并且时间的各个属性用小括弧括起来，即活动1在内部事件1的触发下转移到活动2。

该路由结构中，因为等待状态是一种特殊的动作状态，不具有执行能力，必须等待事件的触发才能跃迁到下一个状态，所以其时间属性将在跃迁上予以表达。即事件触发的开始时间、事件触发的有效时间和事件触发的延迟时间决定该等待状态跃迁的四个时间参数（跃迁最早开始时间、跃迁最晚开始时间、跃迁最早结束时间、跃迁最晚结束时间）。

3 基于时间扩展的UML活动图的工作流过程模型检验

根据文献［10］，同样引入活动间的依赖约束来提高验证的可靠性。在活动图中，一般时间约束只限定在活动状态上，但是本文也将跃迁考虑在内，即对活动状态、跃迁间的约束进行定义。

3.1 约束语义描述

引理1 活动状态的相互依赖时序约束［3］。

约束语义的描述建立在以下引理的基础上：

（1）最大上界upb（i，j）活动状态i和j之间的时间要小于等于该值，表示为｛upb（i，j）｜upb（i，j）∈Z，i∈A∧T，j∈A∧T｝。

（2）最小下界lob（i，j）活动状态i和j之间的时间要大于等于该值，表示为｛lob（i，j）｜lob（i，j）∈Z，i∈A∧T，j∈A∧T｝。

引理2 活动状态之间的距离约束［3］。

（1）最小延迟d（i，j）活动i和j之间的最短时间，表示为｛d（i，j）｜d（i，j）∈Z，i∈A∧T且j∈A∧T｝。

（2）最大延迟D（i，j）活动i和j之间间隔的最长时间，表示为｛D（i，j）｜D（i，j）∈Z，i∈A∧T且j∈A∧T｝。

引理3 依赖约束一致性［3］。

称upb（i，j）（j≥i）满足一致性，当且仅当D（i，j）≤upb（i，j），相应地，当且仅当d（i，j）≥lob（i，j）；称活动i的时间限制满足时间约束一致性，当且仅当TTi≥max｛D（1，i）+AFT1｝。

同时规定活动i和j之间D（i-1，i）=ALT（i）-AFF（i-1）；活动i和j之间d（i-1，i）=AFT（i）-ALF（i-1）；同时把并行和选择结构看作复合的活动，这样，如果活动i到j是连通的，则i和j之间的所有D值之和等于D（i，j），同理活动i到j之间的所有d值之和等于d（i，j）。这样，对于upb和lob，可以通过求和计算来验证是否满足一致性；对于TT，计算出D（1，i），将其值与活动a1的最小开始时间AFT（a1）求和，然后与TT（i）比较，来检查是否满足一致性。

3.2 验证规则

依据上述的引理，对工作流中的顺序关系、嵌套（并行关系）进行验证规则的定义，具体如下：

（1）顺序关系

工作流中最简单的关系属顺序关系，它们之间不存在相互嵌套，这样的活动有1个必要条件和2个验证规则。顺序关系的必要条件（对于活动而言）为

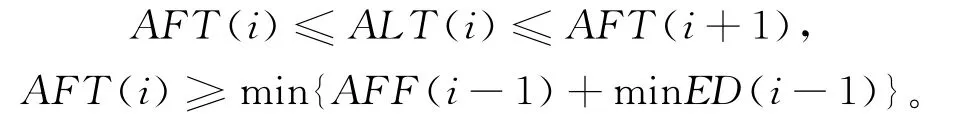
规则1 如果AFT（i）≥max｛TT（i-1）+EFF（i-1）｝，则活动i满足约束。

规则2 如果每项活动4个参数（最早开始时间AFT、最晚开始时间ALT、最早完成时间AFF、最晚完成时间ALF）之间存在关系AFT≤ALT≤ALF≤TT，且AFT≤AFF≤ALF≤TT，同时两项活动i和j之间也有ALF（i）≤AFT（j）（i≤j），则i和j满足时序一致性。

（2）嵌套或并行关系

对于嵌套或并行的任务，如果用上述4个参数验证，则情况过于复杂，可以通过任务间的依赖约束来验证，规则如下：

规则3 4个任务（i，j，k，l）组成两个约束X和Y。X表示i和j之间的约束，Y表示k和l之间的约束。嵌套如图8 所示。当且仅当D（k，i）+upb（i，j）+D（j，l）≤upb（k，l）时，称X和Y间的时序依赖是一致的。

4 实例验证

4.1 基于时间扩展的UML活动图的工作流过程建模

以西安某制造厂的设计制造一体化工作流程为例进行建模。

在制造业各个流程中，角色的到达时间一般均不可估计，一般可将其设为未知数，之后的八个参数通过角色到达时间、有效时间、活动延迟时间、跃迁有效时间、延迟时间五个常量计算而来。本文以该企业的设计制造一体化业务流程为例，为了增强本文的可理解性和验证的方便性，假设这一工作流角色的到达时间已知，根据其值可以推出之后的值，从而保证数据的实时性。

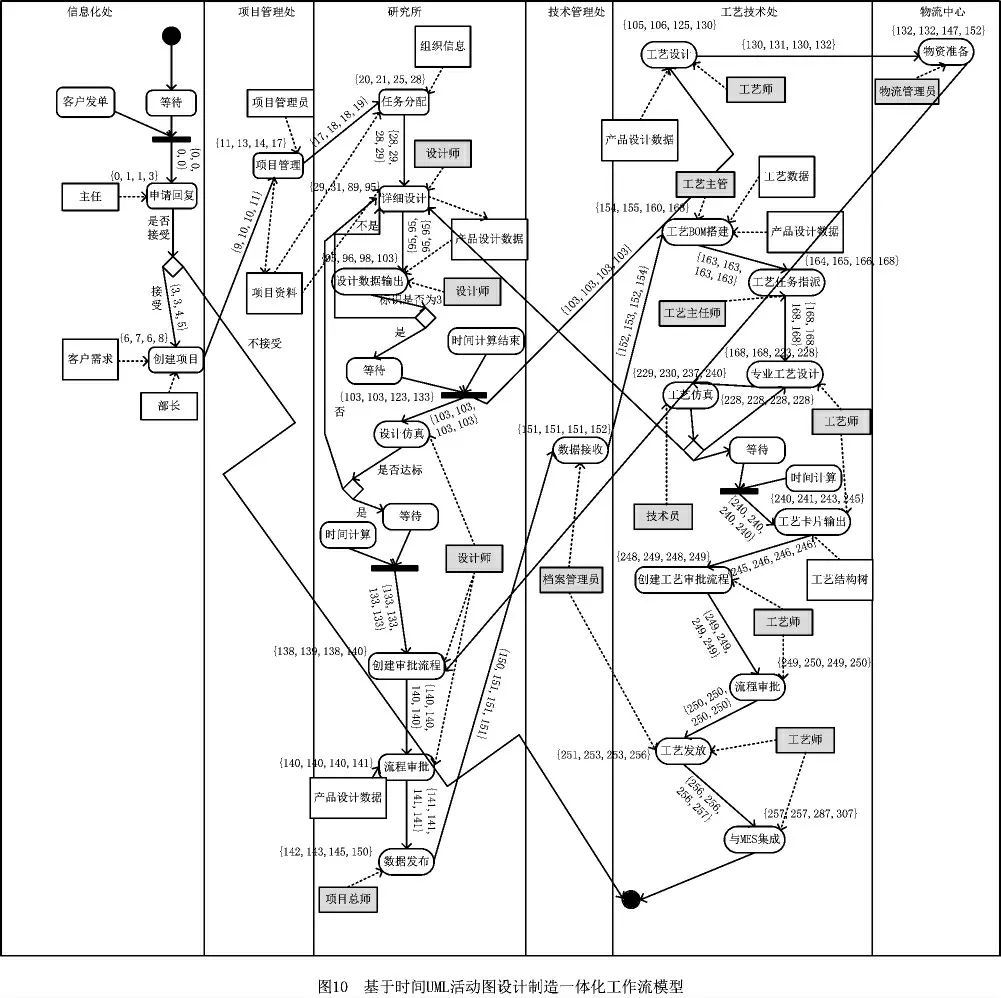
该企业以产品为主线、以项目为单位进行各项活动的运作，其设计制造一体化总共耗时310d，业务流程如图9所示。

此流程的时间基准点为3月1日，时间粒度为d，采用相对时间进行计算。通过对以上设计制造一体化工作流程进行分析，建立如图10所示的基于时间UML活动图的工作流模型，并根据本文所改进的检验方法，检验其工作流的时间一致性，以保证工作流模型时间因素的正确性、有效性和一致性。

4.2 模型验证

利用本文改进的验证引理，对实例中的UML活动图的时间约束进行验证：

（1）验证活动的必要条件

1）对于活动1 回复客户需求和活动2 创建项目，a1=｛0，1，1，3｝，t1=｛3，3，4，5｝；a2=｛6，7，6，8｝，t2=｛9，10，10，11｝，有

2）对于活动2创建项目和活动3项目管理，a2=｛6，7，6，8｝，t2=｛9，10，10，11｝；a3=｛11，13，14，17｝，t3=｛17，18，18，19｝，有

3）对于活动3项目管理和活动4任务分配，a3=｛11，13，14，17｝，t3=｛17，18，18，19｝；a4=｛20，21，25，28｝，t4=｛28，29，28，29｝，

4）对于活动4任务分配和活动5详细设计，a4=｛20，21，25，28｝，t4=｛28，29，28，29｝；a5=｛29，31，89，95｝，t5=｛95，95，95，95｝，有

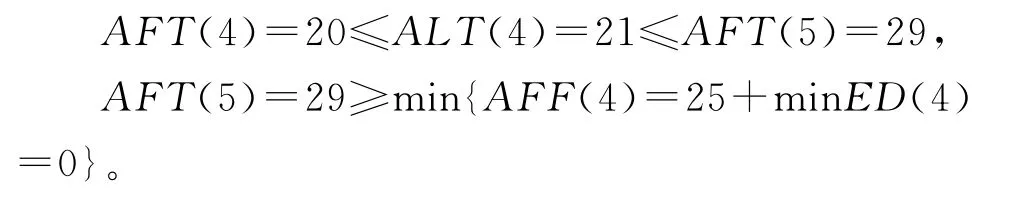
5）对于活动5详细设计和活动6设计输出，a5=｛29，31，89，95｝，t5=｛95，95，95，95｝；a6=｛95，96，98，103｝，t6=｛103，103，103，103｝，有

6）对于活动6设计输出和活动10设计仿真，a6=｛95，96，98，103｝，t6=｛103，103，103，103｝；a10=｛103，103，123，133｝，t10=｛133，133，133，133｝，有

同理，对活动7～活动27进行必要性计算和检查，发现顺序路径上的所有活动都满足必要条件。

（2）对每个活动计算D，根据规则1验证其截止期限

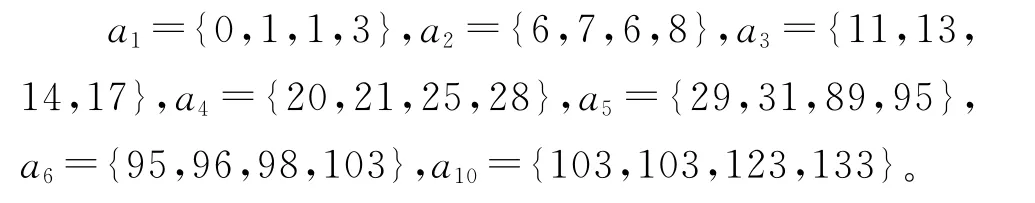
1）活动1需求回复

2）活动2创建项目

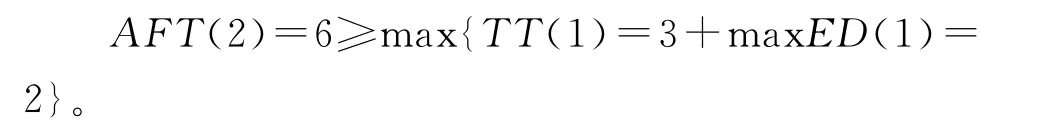
3）活动3项目管理

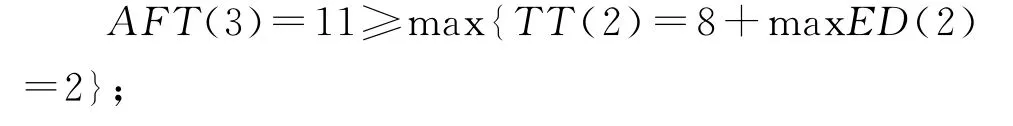
4）活动4任务分配

5）活动5详细设计

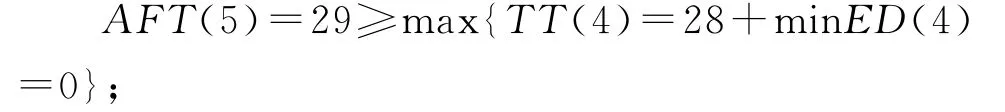
6）活动6设计输出

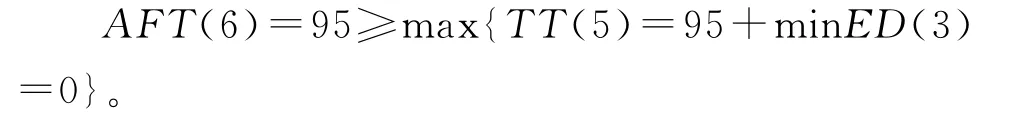
同理，活动7～活动27满足截止日期的一致性约束。验证截止日期：

TT（2）=8≥D（1，2）=5+AFT（1）=0，活动2满足截止时间约束；

TT（3）=17≥D（2，3）=7+AFT（1）=0，活动3满足截止时间约束；

TT（4）=28≥D（3，4）=7+AFT（1）=0，活动4满足截止时间约束；

TT（4）=28≥D（1，2）=5+D（2，3）=7+D（3，4）=7+AFT（1）=0，活动4满足截止时间约束。

以此类推，TT（27）=307≥D（1，27）=256+AFT（1）=0，即整个工作流程满足截止时间约束。

（3）验证活动之间的时序一致性

1）活动1回复需求

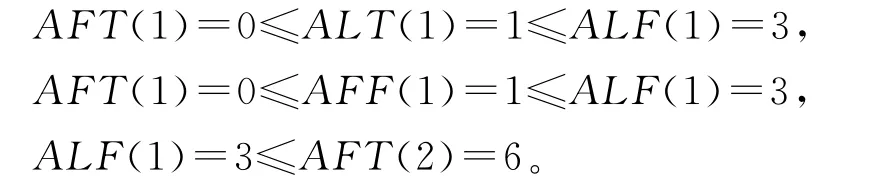
2）活动2创建项目

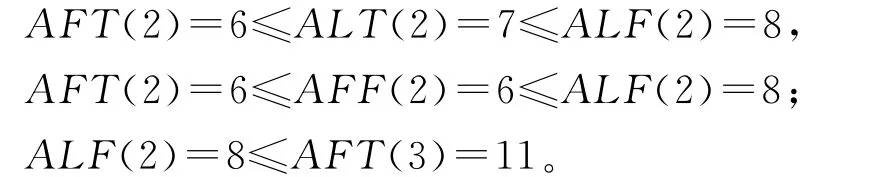
3）活动3项目管理

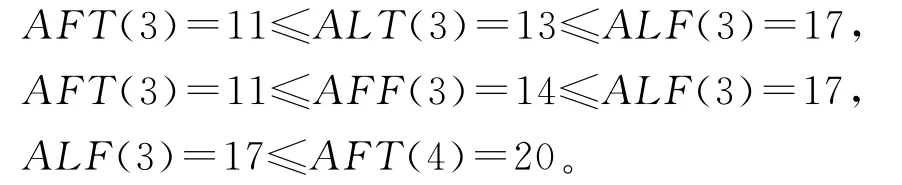
4）活动4指派任务

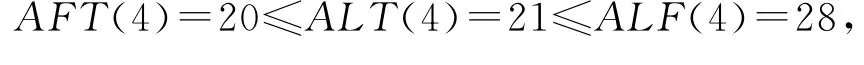
5）活动5详细设计

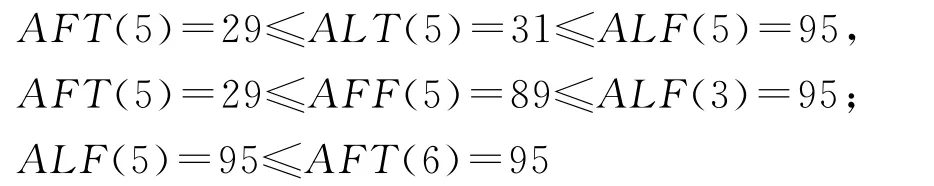
6）活动6设计输出

同理，经验证活动7～活动27满足活动时序一致性。

（4）验证嵌套或并行任务间依赖的一致性

在设计制造一体化过程流程中，设计数据输出活动6将所产生的设计数据信息并行转移到设计仿真活动10和工艺初步规划活动8两种活动。

根据规则3，X表示设计数据输出活动6 与设计仿真活动10之间的约束，Y表示详细设计活动5和创建审批流程15之间的约束。

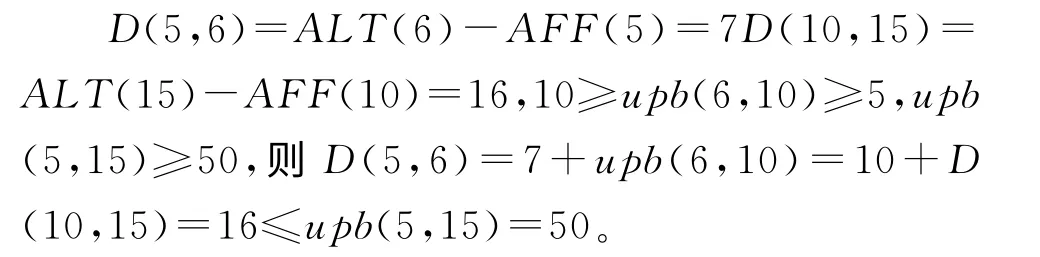
同理，经过检验，并行详细设计活动5、数据输出活动6、工艺初步规划活动13和创建审批流程活动15遵循时间约束一致性。

5 结束语

本文基于企业所面临的时间问题，综合考虑流程中遇到的时间因素，对UML 活动图进行扩展。本文方法的优点在于：①在考虑活动状态所具有的时间因素的同时，也考虑了活动转移的时间约束；②针对活动和转移的时间约束，考虑影响时间的6种因素（活动中资源到来时间、资源的有效时间、活动的延迟时间、跃迁的有效时间、跃迁的延迟时间、活动的截止时间），通过语义形式进行描述，并计算出活动的最早开始时间、最晚开始时间、最早结束时间、最晚结束时间，跃迁的最早开始时间、最晚开始时间、最早结束时间、最晚结束时间，在时间上加强了活动与转移之间的紧密型；③除了对6种路由进行时间扩展外，提出基于等待状态事件触发活动转移路由，解决了循环活动事件时间计算的问题。最后利用改进的时间一致性检验方法，通过实例应用，对所提方法进行检验，验证了其正确性、有效性和一致性。

本文存在以下不足：①未能对UML 活动图的工作流流程模式进行详细描述与改进；②建模的目的除了能够对业务流程有清晰的认识外，主要为系统的设计、流程的优化提供有力的支持，因此本文缺乏对系统设计方面的研究。

未来将着重以该模型为基础，不断优化工作流程的流动模式，同时逐步完成工作流引擎的设计与实现。因此，为了使模型与引擎能够达到完美的配合，今后会将本文建立的工作流模型通过接口转换为基于XPDL（extensible markup language process definition language）的XML文档，实现模型中的活动、过程与引擎中的活动、过程的完美映射，以达到模型与引擎的自动交互，最终完成基于时间约束的工作流引擎的开发工作，从而更好地管理制造企业业务流程中的时间问题，提高企业生产效率、降低企业生产成本、缩短产品生产周期。

［1］WANG Xiaohua.Modeling method of workflow process based on extended UML activity diagram［D］：Chongqing：Chongqing University，2005（in Chinese）.［王小花.基于扩展的UML活动图的工作流过程建模［D］：重庆：重庆大学，2005.］

［2］DUMANS M，TER HOFSTEDE A H M.UML activity diagrams as a workflow specification language［J］.Lecture Notes in Computer Science，2001，2185：76-90.

［3］ESHUIS R，WIERINGA R.A real-time execution semanticsfor UML activity diagrams［J］.Lecture Notes in Computer Science，2001，2029：76-90.

［4］CAI Yan.Comparative analysis of the workflow modeling［C］／／Proceedings of International Conference on Management of e-Commerce and e-Government.Washington，D.C.，USA：IEEE，2012：226-229.

［5］BENGHAZI K，GARRIDO J L，NOGUERA M，et al.Extending and formalizing UML 2.0activity diagrams for the specification of time-constrained business processes［C］／／Peoceedings of the 4th International Conference on Research Challenges in Information Science.Washington，D.C.，USA：IEEE，2010：93-100.

［6］YOUNES A B，AYED L J，HLAOUI Y B.UML AD refinement patterns for modeling workflow applications［C］／／Peoceedings of the 36th Annual Computer Software and Applications Conference Workshops.Washington，D.C.，USA：IEEE，2012：236-241.

［7］LIU Xiao，YANG Yun，JIANG Yuanchun，et.al.Preventing temporal violations in scientific workflows：where and how［J］.IEEE Transaction on Software engineering，2011，37（6）：805-825.

［8］CUI Meng，YUAN Hai，LI Xuandong，et al.Analyze on timing constraint UML activity diagram model［EB／OL］.［2013-03-21］.http：／／d.g.wanfangdata.com.cn／Conference ＿3511043.aspx（in Chinese）.［崔 萌，袁 海，李宣东，等.带时间约束的UML 活动图模型的分析［EB／OL］.［2013-03-21］.http：／／d.g.wanfangdata.com.cn／Conference＿3511043.aspx.］

［9］YU Jia.Study on workflow model based on time Petri net［D］.Hangzhou：Zhejiang Industry and Commerce University，2010（in Chinese）.［虞 甲.基于时间Petri网的工作流模型研究［D］.杭州：浙江工商大学，2010.］

［10］LI Dan，CHEN Qizhang，LIU Qiang.Research and verification of Petri-net based time model in workflow［J］.Computer Engineering，2007（7）：84-86（in Chinese）.［李 丹，陈启璋，刘 强.一种基于Petri网的时间工作流模型的研究与验证［J］.计算机工程，2007（7）：84-86.］

［11］PANG Hui，FANG Zongde，ZHAO Yong.Simplification analysis and schedulability verification of timing constraint workflow model［J］.Computer Integrated Manufacturing Systems，2008，14（11）：2217-2223（Chinese）.［庞 辉，方宗德，赵 勇.时间约束工作流模型的简化分析与可调度性验证［J］.计算机集成制造系统，2008，14（11）：2217-2223.］

［12］YI Chuntao.The workflow model based on UML activity diagram［D］.Daqing：Daqing Petroleum Institue，2007（in Chinese）.［伊春涛.基于UML 活动图的工作流模型［D］.大庆：大庆石油学院，2007.］

［13］YANG Nianhua，YU Huiqun，SUN Hua，et al.Modeling activity diagrams with extended Petri nets［J］.Intelligent Automation and Soft Computing，2011，17（6）：725-735.

［14］ESHUIS R，WIERINGA.Comparing Petri netand activity diagram variantsfor workflow modelling-aquest for reactive Petri nets［M］.Berlin，Germany：Springer-Verlag，2005：945-953.