一类具有等式约束的带乘性噪声系统的最优滤波算法*

褚东升，于兴凯，张 玲

（中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室，山东 青岛 266100）

目前国内外的众多学者，针对带有约束条件的卡尔曼滤波算法做了大量的研究工作。运用系统特性到实际系统的等式关系，结合卡尔曼滤波算法Tahk［1］，Blair和Alouani寻找解决了目标运动，Chen和Chiang［2］解决了信号失真等问题。Simon D［3］，Chia T L［4］提出状态约束滤波算法和针对统计状态约束条件出现的情况下的约束滤波算法。针对非线性系统Teixeira［5］，Simon D［3］提出了适应于非线性系统的附有状态等式约束条件的状态估计算法。同时众多学者给出许多应用实例。目前处理等式约束卡尔曼滤波问题的主要方法可以归纳为以下几种：伪测量法［1］、数学投影法［6］、减少模型参数化方法、两步约束法［7］、再参数化法。

虽然对带有等式约束动态滤波算法的研究进行了相当长的时间。但带有等式约束动态滤波算法大都建立在线性系统模型之上，而在实际系统中还往往存在着乘性噪声的干扰，观测方程往往本质上是非线性的，而带乘性噪声随机系统的控制和滤波问题研究已广泛应用于石油地震勘探、目标识别、语音处理、水下目标跟踪等领域。针对带乘性噪声系统状态附等式约束的滤波问题是一个新的研究方向。

本文针对乘性噪声系统状态附等式约束的最优滤波算法进行研究。把状态等式约束扩维到观测方程中，然后基于投影定理对扩维后的系统进行最优滤波求解。把求解得到的滤波算法各个量用无约束最优滤波算法的各个量表示出来，得到的算法结果与基于数学最优化理论求解得到的算法进行比较。同时对一个算例进行仿真，验证该算法的有效性。

1 乘性噪声无约束系统的状态滤波算法

对于带乘性噪声的离散随机无约束系统，其状态空间方程表示为

其中：xk∈Rm为状态向量；zk∈Rn为量测向量；wk∈Rr为系统噪声；vk∈Rn为量测噪声；mk为一维乘性噪声；A，C为相应维数的系数阵。设系统满足以下条件：

D5：随机序列 ｛mk｝，｛wk｝，｛vk｝及初始状态x0相互统计独立。

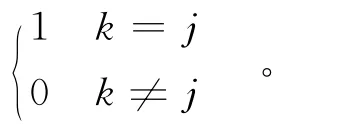
则有系统的状态滤波公式［8］如下：

其中：Dk是s×m阶常量矩阵；dk是s×1阶常向量；s是状态约束量，并且s≤m。本文假设Dk是满秩矩阵，且秩为s阶。

基于（1）、（2）、（9），系统可变形为

其中：xkD∈Rm为状态向量；zkD∈Rn＋s为量测向量；wk∈Rr为过程噪声；vkD∈Rn＋s为量测噪声；mk为一维乘性噪声；A，CD为相应维数的系数阵。设该系统满足以下条件：

D5：随机序列mk，wk，vkD及初始状态x0D相互统计独立。

这里用上标D来表示状态附有等式约束的乘性噪声系统各个量。不加上标表示常量或变量与无约束系统中的量相同。

2 基于投影定理求解最优滤波算法

对（10）、（11）构成的系统用文献［9］介绍的基于投影定理和扩维卡尔曼滤波方法，求得状态最优滤波公式如下：

3 算法比较

根据文献［4，11］用基于数学最优化理论的方法求解系统（1）、（2）、（9）的状态滤波公式，该法是把无约束卡尔曼滤波映射到约束空间中。对于任意时刻k，用xkM/k表示状态受约束的估计值，xk/k表示状态没有约束的状态滤波值，Wk是任意对称正定权重矩阵。

根据这种方法求解得到的状态滤波值为：

根据误差最小化可以得到Wk＝Pk－/k1 时得到的状态滤波值最优。即：

更新后估计误差协方差可用下公式求得：

用文献［4］方法求解可以看到有以下不足之处：

（1）每一步都需要求解无约束系统的状态滤波值和估计误差协方差，增加了计算量；

（2）只是基于数学最优化方法求解状态最优滤波值，没有去考虑整套滤波公式的实时递推；

（3）没有考虑到观测方程对结果的影响。

下面对系统（10）（11）的状态约束滤波公式结果用系统（1）（2）的无约束滤波公式各个量进行表示，寻找其中的联系，并与数学最优化算法的求解结果进行对比分析。假设2个系统k－1时刻（初始启动时刻）的滤波值、误差协方差、状态Sk－1值相同，于是对比k时刻两个系统滤波结果。

假设：

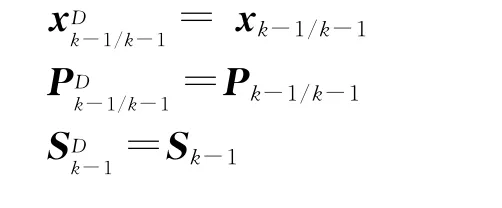
则可以得到：

再求新息：

同时：

根据文献［12］，

由（16）、（17）、（22）、（23）可以求得：

定理1 本文基于投影定理求解的最优滤波算法中增益量（16）与无约束滤波算法增益量（7）有如下关系

证毕。

由（13）、（22）、（24）、（25）可得：

定理2 本文基于投影定理求解的最优滤波算法中滤波值（13）与无约束滤波算法滤波值（4）有如下关系：

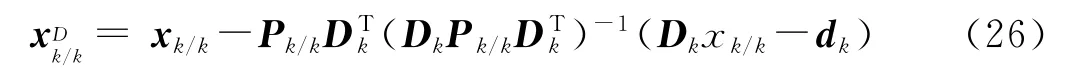
证明

证毕。

定理3 本文基于投影定理求解的最优滤波算法中误差方差矩阵（15）与无约束滤波算法误差方差矩阵（6）有如下关系

证明

由此可得：

证毕。

根据式（19）～（26）可以得到用本文介绍的方法求解的状态最优滤波与无约束状态滤波公式的联系。同时可以看到该法与数学最优化方法求解结果［4，6，11］的不同之处。对比（18）与（25）可得到本文介绍方法得到的状态最优滤波值与文献［4］方法的滤波值在结果上是等价的。不同之处在于式（23）、（24）、（26）表示的变量。

通过对比可以得到本文介绍的算法保证了增益、误差协方差及状态估计值的实时更新特性。同时避免了用无约束滤波值作为中间变量的麻烦，保证算法的简洁精确。减小了计算量和计算误差，提高了算法运行效率。两种方法求得的状态估计值都有以下两个性质［4，11］：

性质1 根据系统（10）、（11）进行滤波得到状态估计值（26）是状态真实值的一个无偏估计。即

性质2 约束卡尔曼滤波估计值的误差协方差比无约束的卡尔曼滤波估计的误差协方差更小。即

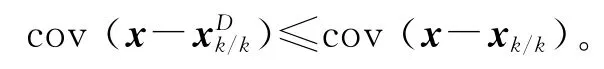
证明过程与参考文献［4，11］推导类似。

4 算例分析

车辆运动系统的状态方程和观测方程给出如下［13］：

假设状态向量x的前2个分量是地面车辆的北坐标和东坐标，后2个分量是北方向速度和东方向速度。由东逆时针测定航向角度θ，汽车沿着角度θ行驶。位置观测设备给出了带观测噪声的北方向和东方向位置值。

其中T表示离散步长，即历远间隔，设T＝1s。取θ＝π/3。过程噪声协方差为Qk＝Diag（4，4，1，1），观测噪声协方差为Rk＝Diag（5，5）。乘性噪声均值为＝2，方差为＝0.2。初始估计误差协方差P0＝Diag（9，9，4，4）。根据实际情况，如果知道汽车行驶在航向角为θ的道路上，可以得到tanθ＝x1/x2＝x3/x4。由此可得到等式约束Dkxk＝dk。其中

利用Matlab分别对基于数学最优化理论算法［4］和本文中基于投影定理的算法进行仿真，历元总数为300s，北方向和东方向绝对误差如图所示。其中红线代表本文算法绝对误差，蓝线代表数学最优化理论算法绝对误差。

通过图1和2可以看出前2个状态在2种算法下绝对误差的大小，可以很直观的看到本文算法优于文献［3］算法，说明了本文算法的有效性。考虑到信噪信噪比（SNR）对滤波结果的影响。本文做了大量的仿真实验，表一给出前2个状态量在不同信噪比及不同算法下误差的平均值大小。从表1中可以看出，信噪比越大，滤波误差平均值越小，即滤波效果越好。同时通过对比可以直观得到本文算法的有效性。

仿真中乘性噪声解释为观测中存在的信号的延迟、信道的衰减及无关数据的干扰等复杂因素的综合。以上仿真结果验证了本文算法的有效性，通过多次仿真本文算法的高效性也可以体现。同时在仿真中也显现出来了该方法的不足，在信噪比较小（小于10－2）时，仿真对比效果不明显，所有算法效果都不好。对于信噪比很小的特殊情形有待进一步研究。

图1 北方向位置绝对误差Fig.1 The absolute error of North position

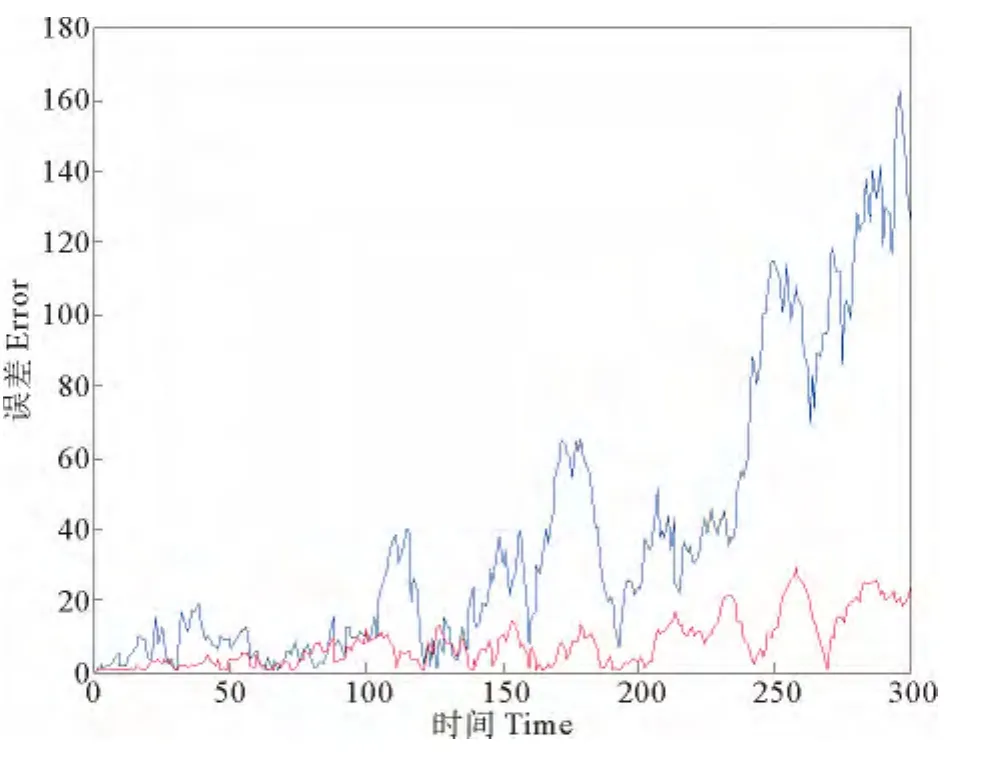
图2 东方向位置绝对误差Fig.2 The absolute error of East position

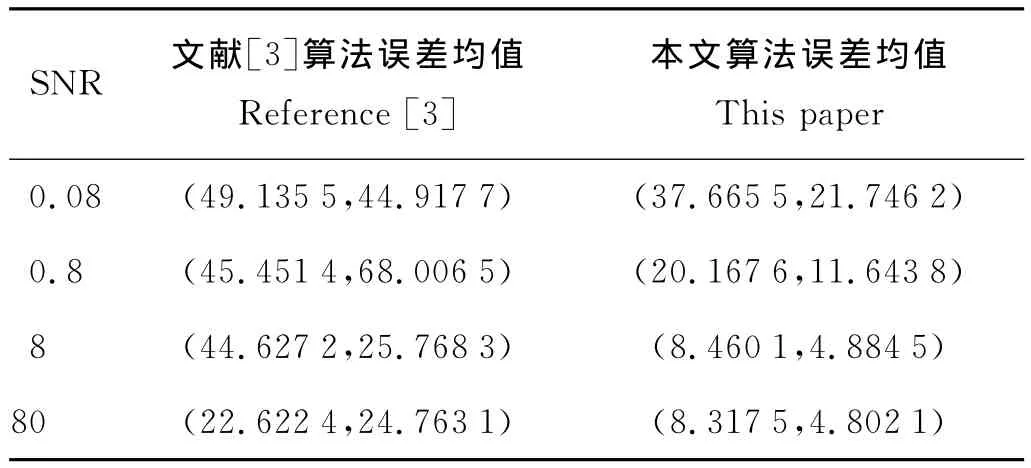
表1 不同信噪比滤波误差均值的大小Table 1 Filtering average error average with different signal to noise ratio

5 结语

本文给出了在乘性噪声系统中状态附等式约束的一套最优滤波算法。该算法是通过把状态等式约束扩维到观测向量中，利用投影定理对变形后的系统进行最优滤波求解。进一步把得到的算法各个量用无约束滤波算法对应各个量表示出来，并与无约束滤波算法和基于数学最优化理论方法得到的算法进行比较分析验证该算法的更新特性和简洁有效性。实例仿真进一步验证了该算法误差小、效率高的特性。本文介绍的等式约束是线性的，对于带乘性噪声系统非线性的等式约束问题有待进一步研究。

［1］Tahk M，Speyer J L.Target tracking problems subject to kinematic constraints［J］.IEEE Tram Automat Cont，1990，35（3）：324-326.

［2］Chen Y H，Chiang C T.Adaptive beamforming using the constrained Kalman filter［J］.IEEE Transaction on Antennas and Propagation，1993，41（11）：1576-1580.

［3］Simon D，Chia T L.Kalman filtering with state equality constraints［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（1）：128-136.

［4］Chia T L，Simon D，Chizeck H J.Kalman filtering with statistical state constraints［J］.Control and Intelligent Systems，2006，34（1）：73-79.

［5］Teixeira B O S.State Estimation for Equality-Constrained Linear Systems［C］.LA：Proceeding of the 46th IEEE Conference on Decision and Control New Orleans，2007：12-14.

［6］Simon D.Kalman filtering with state constraints：a survey of linear and nonlinear algorithms［J］.IET Control Theory and Applications，2010，4（8）：1303-1318.

［7］Simon J，Julier Joseph J，LaViola Jr.On Kalman filtering with nonlinear equality constraints ［J］.IEEE Transaction on Signal Processing，2007，55（6）：2774-2784.

［8］褚东升，张玲.通道相关时带乘性噪声系统最优滤波 ［J］.青岛海洋大学学报，2002，32（6）：987-992.

［9］宋文尧，张牙.卡尔曼滤波［M］.北京：科学出版社，1991.

［10］Benzi M，Golub G H，Liesen J.Numerical solution of saddle point problems［J］.Acta Numerica，2005，14（1）：1-137.

［11］Simon D.Kalman filtering with state constraints［J］.IET Control Theory Appl，2010，4（8）：1303-1318.

［12］Gupta N，Hauser R，Johnson N F.Forecasting Financial Time-Series using Artificial Market Models［C］.Oxford na-tr：Proceedings of the 10th Annual Workshop on Economic Heterogeneous Interacting，2005，05/09.

［13］宋迎春.动态定位中的卡尔曼滤波研究 ［D］.长沙：中南大学，2006.

［14］Chun Yang，Erik Blasch.Kalman filtering with nonlinear state constraints［J］.IEEE Transactions On Aerospace and Electronic Systems J，2009，45（1）：70-84.