基于多属性系统结构模型的火力打击方案评估＊

（海军陆战学院 广州 510430）

1 引言

未来渡海登岛作战中，舰炮火力是支援登陆兵作战的一支重要火力打击力量［1～2］。由于涉及的因素繁多，各种关系错综复杂，如何科学、合理地使用舰炮火力是一个复杂的系统分析问题［3～5］。为了更好地发挥舰炮火力在登陆作战中的重要作用，根据系统论的相关原理，本文通过建立多属性的系统结构模型，对舰炮火力打击方案进行评估研究，以期为指挥员合理使用舰炮火力提供科学的决策依据。

2 多属性的系统结构模型

系统结构模型是对问题系统进行分析的最基本的描述性模型，它描述了系统各要素之间的关系，记录了对系统结构定性关系的认识，同时它又是激发和诱导进一步分析系统的媒介。因此，如果能够准确识别系统的构成要素，以及描述要素功能和状态的属性，就可以运用该模型解决实际问题［6～7］。

2．1 多属性的系统结构模型建立

建立系统结构模型，首先应识别出系统构成要素并对每个要素通过描述其功能和状态给出要素的属性。在识别出系统构成要素及每个要素的各属性后，以要素的属性为准则，按照两两比较方法建立模糊关系矩阵，具体步骤如下［8～9］：

1）在系统的n个构成要素S1，S2，…，Sn中任选一个要素Sk为参考点。

2）对于参考点Sk，考虑那些对它有影响的n′个要素，并依次以它的第l个属性，不妨假定l＝1，2，…，m为准则，进行两两比较，判断哪一个要素对参考点Sk的属性影响更大，大多少。若对两两比较结果采用1～9的比例标度来描述，可得到判断矩阵：

3）求判断矩阵的最大特征值及其对应的特征向量，即：

4）检验判断矩阵的一致性。若一致性指标C．Ⅰ．与平均随机一致性指标R．Ⅰ．之比小于0．1，则满足一致性检验。一致性指标C．Ⅰ．按下式计算：

重新编写下标，上式可写成如下形式：

式中≥0。这样，扩充向量rk，l就能全面反映出这n项要素对要素Sk的属性的影响程度。

6）重复上述步骤，可以得到要素对属性的模糊关系矩阵：

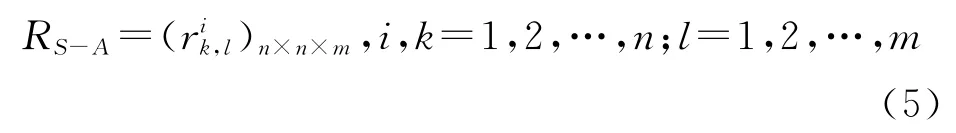
进一步，可以将要素Si对要素Sk的属性的影响程度按照要素Si的属性（j＝1，2，…，m）分解成要素Si的属性对要素Sk的属性Akl的影响程度。在分解时，首先，通过两两比较方法确定其对要素Sk的属性的影响权重，且＝1，然后，按权重确定，即这样就可得到属性对属性的模糊关系矩阵RS-S＝i，k＝1，2，…，n；j，l＝1，2，…，m。

2．2 系统要素及其关联度模型

关联度反映了各要素之间相互影响、相互联系的紧密程度。因此本文定义要素Sk的关联度RLk为该要素Sk的输出信息与输入信息之和，它反映出该要素Sk与哪些要素联系多以及联系程度，因此，它也反映出该要素的信息占有量和信息处理能力［10～11］。

对于要素Sk，属性的输出信息应反映出该属性对所有其它要素的支配情况。如果该要素的属性对其它要素的个属性有影响，则：

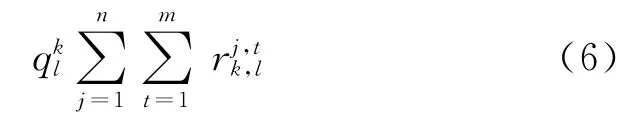
就是要素Sk的属性的输出信息。

对于要素Sk，属性的输入信息应反映出该属性接受所有其它要素支配的情况。如果该要素的属性受到其它要素的个属性的影响，则：

就是要素Sk的属性的输入信息。所以该要素的关联度RLk可表示为

由于在模糊关系矩阵RA-A中关于属性下标都是规范化的，则有：

若用表示要素Sk的属性的关联程度，则有下式成立：

这样，利用式（10）就可以分析要素Sk的关联程度的构成，指明哪些属性的关联度处于主导地位。

3 实例分析

在一次登陆作战中，红方舰艇部队利用先进的侦察情报系统，获取了登陆兵作战地域内敌目标情况，确定敌集结坦克阵地（S1）、指挥所（S2）、交通枢纽（S3）、炮兵阵地（S4）四类目标作为敌防御体系中的重要节点予以打击。在此，把这四类目标看作敌防御体系的四个要素，而要素中的不同目标，可看作描述要素的不同属性，例如敌集结坦克阵地（S1）包含四个连阵地：坦克1连（A11）、坦克2连（A12）、坦克3连（A13）和坦克4连（A14），即把它们描述为要素S1的四个属性。虽然表面上看这些目标之间好像没有什么联系，但为达成共同的防御作战目的，作战任务使它们成了密不可分的整体。在确定了敌防御体系的构成要素及每个要素的各属性之后，以要素的属性为准则，按照两两比较方法建立模糊关系矩阵，具体步骤如下：

第一步：分别选择敌防御体系的四个要素S1、S2、S3、S4作为参考点，并以它们的各个属性为准则，经专家两两比较打分得出各属性的判断矩阵如下：

第二步：求各个判断矩阵的最大特征值及其对应的特征向量，满足一致性检验之后，扩充得到要素对属性的模糊关系矩阵RS-A，如表1所示。

表1 要素对属性的模糊关系矩阵RS-A

第三步：确定各要素内部属性对要素的影响权重，经专家两两比较打分得出各要素属性之间的判断矩阵Pi（i＝1，2，3，4）如下：

计算各判断矩阵的最大特征值及其对应的特征向量，经一致性检验之后，求出各个属性对要素的影响权重：

要素S1的各个属性A11、A12、A13、A14对其的影响权重分别为：0．2246、0．1658、0．1101、0．4995；

要素S2的各个属性A21、A22对其的影响权重分别为：0．75、0．25；

要素S3的各个属性A31、A32、A33、A34对其的影响权重分别为：0．4755、0．1585、0．0915、0．2745；

要素S4的各个属性A41、A42、A43对其的影响权重分别为：0．4286、0．2271、0．3443。

第四步：通过权重将要素对属性的模糊关系矩阵RS-A分解成属性对属性的模糊关系矩阵RS-S，如表2所示。

表2 系统结构模糊关系矩阵RS-S

第五步：根据多属性的系统结构模型及关联度的计算模型，可以计算出敌防御体系中各目标的关联度，结果如表3所示。

由以上的分析可知，在确定舰炮火力打击方案时，应首先打击S2敌指挥所，表3计算结论表明，指挥所和其它目标的关联度最大，反映了其“神经中枢”作用，其中A21营指挥所关联度最大，应最先摧毁，A22炮兵指挥所次之。其次是炮兵阵地目标，说明现代海战中火力作战单元发挥着非常重要的作用，交通枢纽和敌集结坦克阵地两者关联程度稍小。

表3 要素及属性的关联度

4 结语

敌防御体系是由若干相互联系、相互作用的目标单元综合集成的具有一定结构形式的有机整体，为达成对敌重要目标节点予以打击以实现体系破击的目的，根据系统论的相关原理，本文将敌防御体系这个“大系统”分解成若干个“小系统”来研究。通过建立多属性的系统结构模型，揭示了敌防御体系中各目标之间的影响关系，分析了各目标对整个体系的关联、贡献等问题，从而为舰炮火力的合理优化使用提供决策依据。

［1］郝子舟，霍高珍．战术学教程［M］．北京：军事科学出版社，2000：121-137．

［2］谭安胜．水面舰艇编队作战运筹分析［M］．北京：国防工业出版社，2009：269-335．

［3］邵鹏举，潘红华，王志民．舰炮对岸应召射击最优火力分配［J］．指挥控制与仿真，2008（5）：40-42．

［4］蔡鸥，马墨翰，岳峰，等．炮兵计划火力的目标选取方法［J］．火力与指挥控制，2007（12）：136-139．

［5］赵敬宝，李斌，吴映军，等．炮兵火力打击决策方案优选的方法［J］．弹道学报，2005（4）：79-83．

［6］谭璐，姜璐．系统科学导论［M］．北京：北京师范大学出版社，2009：119-136．

［7］谭跃进，陈英武，罗鹏程，等．系统工程原理［M］．北京：科学出版社，2010：55-62．

［8］张最良，李长生，等．军事运筹学［M］．北京：军事科学出版社，1999：403-411．

［9］周杰．矩阵分析及应用［M］．成都：四川大学出版社，2008：71-108．

［10］杜栋，庞庆华．现代综合评价方法与案例精选［M］．北京：清华大学出版社，2005：5-18．

［11］马亚龙，邵秋峰，孙明，等．评估理论和方法及其军事应用［M］．北京：国防工业出版社，2013：182-195．