2D雷达与红外异地配置下的航迹关联方法＊

宋君才 沈正华 李 峰

（1．驻上海地区水声导航系统军事代表室 上海 200136）（2．上海航海仪器有限责任公司 上海 200136）

1 引言

在目标跟踪中，由雷达和红外传感器组成的系统，是一种典型的异类多传感器融合系统。如何充分发挥红外、雷达两种传感器的互补性，使其相得益彰，是近年来国内外专家研究的热点。然而，异类传感器信息融合却面临着许多困难，其最主要的困难是目前尚没有统一的数学工具与方法［1～2］。因此，我们对于异类传感器信息融合只能针对具体的对象进行融合方法的讨论。文献［3］分析了同平台集中式单目标雷达／红外双传感器融合跟踪算法；文献［4～5］讨论了不同平台雷达与红外传感器通过所在位置的转换测量和相应的测量误差进行航迹融合。由于2D雷达和红外传感器的探测信息都不能完整表达一个三维空间目标的位置：前者缺乏仰角信息，坐标转换误差较大；后者没有距离信息，不能进行坐标转换；从而导致了融合性能的下降［6］。

针对不同平台2D 雷达与红外传感器航迹关联问题，本文提出一种基于假设检验的异类传感器航迹关联算法，该方法在假设条件下通过纯方位交叉定位获得传感器量测空间的平面公共向量，再结合高精度红外测角与雷达的测距信息，分别获得各自垂直向量的估计，最后根据垂直向量的相似程度判断航迹是否真正关联。仿真实验证明，该方法简单有效。

2 问题描述

设2D 雷达位于（x1，y1），其测距和方位误差是相互独立的零均值高斯分布随机变量，方差分别为；红外传感器位于（x2，y2），其方位角和仰角误差也是零均值高斯分布随机变量，方差为，。雷达关于目标距离和方位测量值分别为d1，α1，红外传感器关于目标的方位和仰角测量分别为α2，β2。由于本文主要讨论2D 雷达与红外传感器的航迹关联问题，因此忽略时间对准［7］问题。

因此，对于异地配置的2D 雷达与红外传感器航迹关联问题，就是要判定t时刻来自2D 雷达的探测信息与来自红外传感器的探测信息是否代表相同的目标。

3 航迹关联方法

3．1 建立关联假设条件

2D 雷达探测航迹对应一个目标，红外传感器探测航迹对应一个目标，将2D 雷达航迹与一个红外传感器航迹的关联问题就转化为一个如下的假设检验问题：

H0：假设2D 雷达航迹与红外航迹关联，且＜，则2D 航迹与红外航迹关联成功；

H1：假设2D 雷达航迹与红外航迹关联，有≥，则2D 航迹与红外航迹关联失败。3．2 方位交叉定位

首先通过2D 雷达与红外传感器探测的方位角信息进行交叉定位，如图1所示。

图1 2D 雷达与红外传感器空间位置分布

根据假设前提，2D 雷达探测目标与红外传感器探测目标已是同一目标，则方位交叉位置为（x，y），可建立方程式如下：

利用式（1）与式（2）联立可计算获得x和y值。

3．2 目标高度估计

假设2D 雷达与红外传感器探测目标交叉位置为（x，y，z），在3．1节中，利用两个传感器的方位信息获得了量测空间的平面向量（x，y）；在本节中，利用2D 雷达的测距和红外传感器的测角信息分别获得各自的垂直向量z。

建立方程式如下：

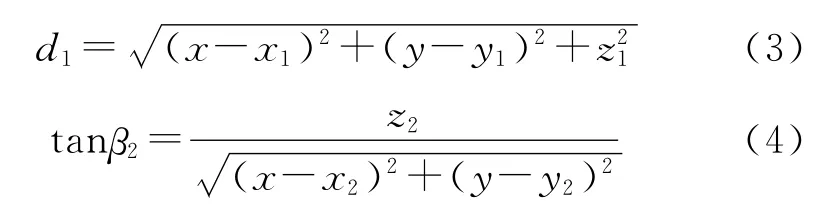
由式（3）可以求得2D 雷达探测目标的垂直向量z1，由式（4）可以求得红外传感器探测目标的垂直向量z2。

3．3 目标高度相似度计算

从3．1节与3．2节中可以获得2D 雷达探测目标信息为（x，y，z1），红外传感器探测目标信息为（x，y，z2），其中（x，y）为两传感器方位信息共同计算获得，而z1，z2是分别利用了2D 雷达的测距和红外传感器的测角信息获得，最后通过对z1与z2相似度的判定确定航迹是否关联。

由式（1）～（4）联立可以获得z1，z2的函数，即

记z＝z1-z2，则：

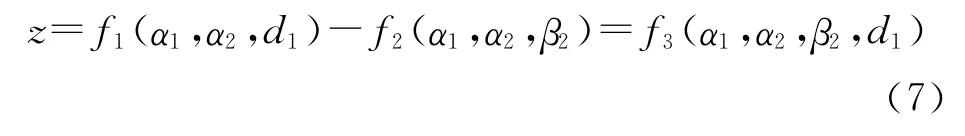
Δz的定位误差为［8］

该定位误差是零均值的随机变量，其方差为

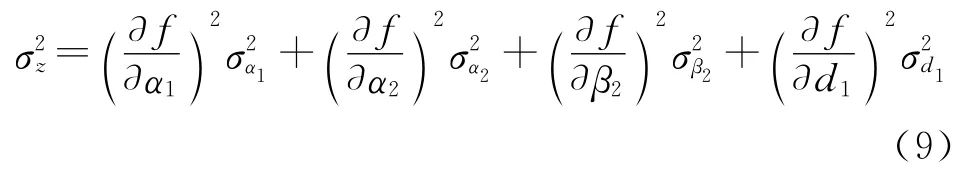
z1，z2是否关联？根据“最近邻”的思想，给定统计距离定义为新息向量的加权范数＝，其中，表示残差向量，Sk为新息协方差矩阵，为残差向量的范数，可以理解两探测航迹之间的统计距离。是一个归一化的随机变量。当为正态分布时，则＝x服从自由度为M的χ2分布的概率密度函数：

其中，M为测量维数。实际上就是把两个航迹是否落入关联门或波门内的问题变成了一个统计检验的问题。

3．4 假设检验

通过的计算，根据χ2检验可知

若随机变量小于临界值，就认为关联成功，接受检验H0；

若随机变量大于或等于临界值，就认为关联失败，接受检验H1［9］。

这样就把波门的大小与落入概率联系起来了。由以上表达式可以看出，波门的边界与相对应，波门的大小主要取决于测量噪声。临界点可根据自由度M以及给定的落入概率P由χ2分布表中可以查到。

如果在两传感器关联过程中存在多义性问题，则可以取最小的与之对应［10］。

4 数值实验

设红外传感器坐标为R1（0，0）在原点O处，2D雷达坐标为R2（-40km，0），目标相对于原点O的距离为20km、方位分别为0°，10°，20°，30°…340°，350°，仰角为23．5°呈圆形分布。2D 雷达距离误差均方差σd1＝50m，方位误差均方差σα1＝0．25°；红外传感器方位误差均方差σα2＝0．1°，仰角误差均方差σβ2＝0．1°。如表1所示。

在这里我们取自由度M＝1，给定置信水平P＝0．99，得到如下仿真模拟结果。

表1 2D 雷达与红外传感器在不同位置的关联正确率

5 结语

通过上述数据实验可以看出，不同平台2D 雷达与红外传感器在探测不同方位的目标的航迹关联正确率均在93．0%以上，满足实际的要求。本方法充分利用2D 雷达与红外传感器互补性，有效实现不同平台2D 雷达与红外传感器航迹关联，具有一定的工程应用价值。

［1］王国宏，等．雷达与红外数据融合评述［J］．火力与指挥控制，2001，27（3）：3-6．

［2］王国宏，毛士艺，何友．红外传感器目标跟踪算法［J］．火力与指挥控制，2001，26（2）：5-9．

［3］武俊，等．雷达与红外的同步航迹融合［J］．舰船电子工程，2007，27（4）：113-114．

［4］黄宵腾，杨宏文，等．基于两坐标雷达与红外传感器融合跟踪［J］．火力与指挥控制，2006，31（9）：54-57．

［5］车志宇，等．雷达-红外异地配置下的数据融合算法［J］．弹箭与制导学报，2005，25（1）：385-387．

［6］韩崇昭，朱洪艳，段战胜，等．多源信息融合［M］．北京：清华大学出版社，2006：365-423．

［7］Bar-shalom，Y．Fortmann，T．E．Tracking and Data Association［M］．New York：Academic press，1988．

［8］何友，王国红，等．多传感器信息融合与应用［M］．北京：北京电子工业出版社，2000．

［9］杨万海．多传感器数据融合及其应用［M］．西安：西安电子科技大学出版社，2004，4：77-81．

［10］胡淑礼．模糊数学及其应用［M］．成都：四川大学出版社，1994：12．