基于时间序列分析的年最大流量预测

吴士夫，伏 琳，罗 兴

（1.长江委水文中游局赤壁分局，湖北 赤壁 437302；2.长江委水文中游局河道勘测中心，武汉 430012）

水文时间序列中的暴雨序列、年最大洪峰流量序列等几乎都是非线性、非平稳、弱相依且高度复杂的时频多变序列［1］，对非平稳时间序列进行分析，具有重大的意义。本文应用时间序列分析方法，将年最大流量时间序列分解为趋势序列、周期序列和平稳随机序列，并采用时序递阶组合模型来预测。

1 时序递阶组合模型的建立

水文时间序列x（t），一般由趋势项f（t），周期项p（t）和随机项η（t）组成，可以用以下组合模型描述：

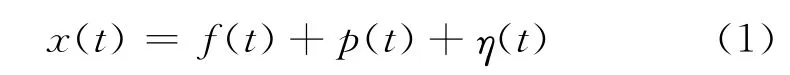
趋势项反映的是水文现象因水文或气象因素而引起的季节性趋势或多年变化趋势，周期项反映的是水文现象的周期性变化，这两项反映的是水文时间序列变化中的确定性成分。通过对序列趋势项、周期项的识别和提取，剩余系列就是随机项，可用平稳的时间序列来分析。在此基础上建立时序递阶组合模型，即可对年最大流量进行预测。

1.1 趋势项分析

时间序列的趋势性可以通过斯波曼（Spearman）秩次相关检验、肯德尔（Kendal）秩次相关检验、滑动平均以及游程检验等方法来检验。本文采用Kendall秩次相关检验法［2］进行趋势性识别。

Kendall秩次相关法是建立在连续实测值的比例数基础上，是一种非参数统计检验法。对于水文序列xi，先确定所有对偶值（xi，xj；j＞i，i＝1，2，…，n－1；j＝i＋1，i＋2，…，n）中的xi＜xj的出现个数p，对于无趋势的序列，p的数学期望值为：

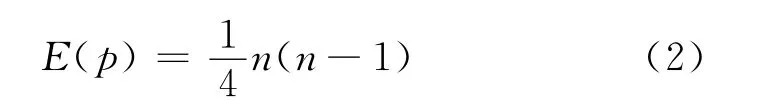
构建Mann－Kendall秩次相关检验的统计量：

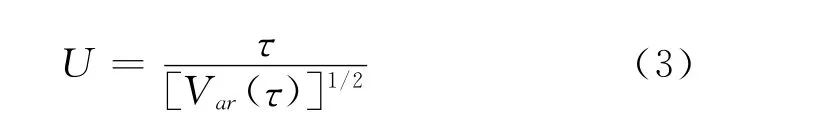
当n增加时，U很快收敛于标准化正态分布。假定序列无变化趋势，当给定显著水平α后，可在正态分布表中查得临界值Ua／2，当｜U｜＞Ua／2时，拒绝假设，即序列的趋势性显著。反之，趋势不显著。

确定序列存在趋势项之后，一般采用线性关系式、对数关系式、指数关系式或者多项式关系式来对趋势项进行曲线拟合。

1.2 周期项分析

水文时间序列经分离出趋势项后，将剩余的序列进行周期分析，本文采用方差分析法［3］分析水文时间序列的周期性，方法简述如下。

（1）识别最大可能的周期数K。

则序列中可能存在的周期长度为2，3，4，…，［N／2］。

（2）按试验周期排列数据，计算组间和组内离差平方和。

式中，j表示组别，j＝1，2，…，b表示分为b组；i为每组含有的项数，i＝1，2，…，aj表示每组有aj个数据。

（3）计算试验周期的方差比。

式中，f1＝b－1，表示组间自由度，f2＝n－b，表示组内自由度。

（4）F检验确定显著周期。选定某一信度α（常取0.05或0.1）。由α，f1，f2查F分布表，可得该信度下F值。若F＞Fα，则该试验周期显著；若F＜Fα，则该试验周期不显著。

（5）从所有的显著试验周期中选择F最大的试验周期为第一周期，并将其从初始序列中滤去。将剩余序列再重复上述步骤，直至不存在显著周期。

（6）将各周期值叠加并外推，即可拟合周期项并进行周期项预报。

1.3 随机项分析

水文时间序列经适当的提取趋势项和周期项后，剩余的最终余波即为平稳随机序列，因此可用线性自回归模型AR（p）对其进行拟合和预报。

（1）模型的建立。

自回归模型AR（p）的形式为：

式中，bp，i（i＝1，2，…，p）为自回归模型系数，p为模型阶数，ε（t）为残差项，自回归模型系数可通过建立Yuler－Walker方程组［4］，采用下列递推公式求得：

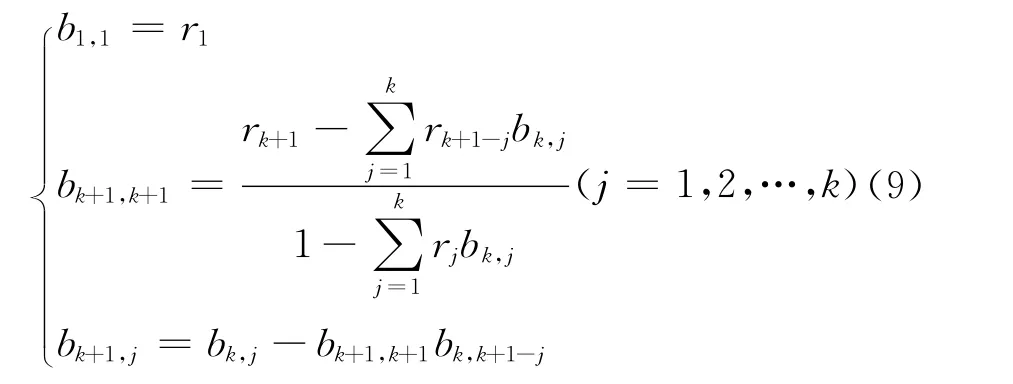
式中，rk为序列的k阶自相关系数，用下式计算：

（2）模型的识别。

模型阶数p的识别，对AR（p）模型来讲甚为重要，可用FPE（最终预报误差）准则来确定。

式中，k为所取阶数，n为样本数，为k阶预报误差方差，可由下式算得：

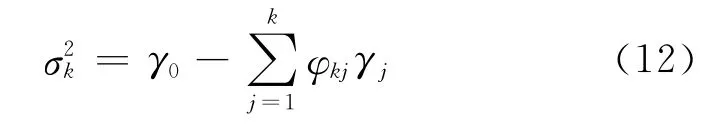
截止阶数p的取法按经验来取。

1.4 预 测

在对最终余波建立合适的AR（p）模型后，便可对最终余波进行预测，设系列在t＋1时刻的预测值为，将它与前面分析的各周期波叠加，再经差分还原计算，即得到最终的预报值，即

式中，pi（t＋1）为周期波i在时刻t＋1的值。

2 年最大流量预测模型的建立与应用

毛家桥水文站位于湖北省崇阳县白霓镇桥局村，是控制陆水水库小港南支高堤河水情的基本站，控制流域面积364km2，是一个典型的山溪性河流测站，水位暴涨暴落，洪峰时间持续较短。

采用毛家桥水文站1961～2010年的年最大流量资料，以1961～2000年共40年的资料建立时序递阶组合模型，用2001～2010年共10年的资料对模型进行检验，以确认模型的精度。

2.1 趋势项分析

根据毛家桥水文站1961～2000年的年最大流量资料，用Kendall相关检验法对其进行分析，计算得Kendall统计量值U＝1.174。

取显著性水平α＝0.05，则相应的检验临界值为Uα／2＝1.96，｜U｜＜Uα／2，即表明毛家桥水文站年最大流量序列不存在明显的趋势成分，无须进行趋势项拟合。

2.2 周期项分析

用方差分析法对年最大流量系列进行周期分析识别，选择信度α＝0.05，经分析，第一周期T＝8，方差比F＝3.902＞F（0.05）＝2.3，第二周期T＝13，方差比F＝2.112＞F（0.05）＝2.07，从年最大流量系列中依次剔除这些周期项后，得到最终余波。

2.3 平稳随机模型的建立

对最终余波进行自回归分析，建立AR（p）模型。通过计算，确定AR（5）模型为最终预报模型，即：

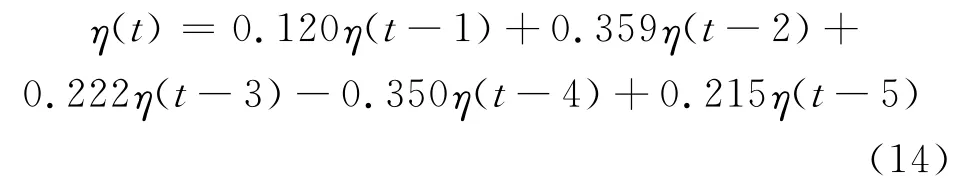
2.4 成果拟合与检验

将8年、13年两个周期波与最终余波的预测值叠加，分别进行模拟和检验，即可得到序列的模拟值和检验值。

利用该组合模型对毛家桥水文站1961～2000年的年最大流量资料进行拟合，用2001～2010年的实测资料对模型进行检验，并将拟合值和实测值进行比较，拟合效果见图1。按20%为允许误差标准，拟合段合格率为82.5%，检验段合格率为70%。模型拟合效果较好，但外延效果一般。

图1 毛家桥水文站时序递阶组合模型预测年最大流量过程

3 总结与讨论

（1）模型拟合效果较好，但外延效果一般。在2001年到2010年共10年的年最大流量预测结果中，前5年预测值相对于实测值的误差都小于10%，预测精度较高。后5年的预测误差较大，这是由于平稳随机序列模型后一年的预测值依赖于前一年的预测值，预测误差存在叠加放大的趋势所致。在实际应用过程中，建议外推年限一般不要超过5年。

（2）时间序列分析方法是一种对历史数据进行分析的数学方法，其精度取决于用于建模的历史数据，资料系列越长拟合精度就越高。一般建议资料系列长度不宜短于30年。

（3）平稳随机序列模型后一年的预测值依赖于前一年的预测值，因此在应用时序递阶组合模型进行外推预测时，应尽可能结合气象要素等的变化特征或近几年水文要素的演变趋势等进行综合分析，并把近年的新序列加到原序列中，重新建立模型，以提高预测的精度。

［1］王义民，张 珏.HHT在年最大洪峰流量规律分析中的应用［J］.计算机工程与应用，2009，45，（34）：204－211.

［2］李春晖，杨志峰.黄河流域分区天然径流量趋势性与持续性特征［J］.水文，2005，25，（1）：13－14.

［3］范钟秀.中长期水文预报［M］.南京：河海大学出版社，1999.

［4］丁 晶，邓育仁.随机水文学［M］.成都：成都科技大学出版社，1988.