多港口挂靠班轮航线配船数学模型及其应用

杜 红， 谢新连， 唐 磊， 赵家保

(大连海事大学 综合运输研究所，辽宁 大连 116026)

谢新连(1956-),男,辽宁大连人,教授,博士生导师,主要从事交通运输规划与管理方面的研究。E-mail: xxlian77@yahoo.com.

多港口挂靠班轮航线配船数学模型及其应用

杜 红， 谢新连， 唐 磊， 赵家保

(大连海事大学 综合运输研究所，辽宁 大连 116026)

为满足班轮运输定时、定期服务的要求，提高班轮运输系统的优化配置水平，根据班轮多港口挂靠与货物直达运输航线形式的特点，综合考虑货运需求、单船最大载货量、最小发船班次、运价水平等多种因素，以研究期内船队营运利润最大为目标，建立班轮航线配船优化数学模型，并系统地介绍建模原理。通过求解算例，验证模型的合理性。计算结果表明：提出的优化方法可有效模拟班轮运输的运营组织特征，有助于制定研究期内航线配船、发船班次的最优方案决策。模型结构简洁、易于理解、求解便利、实用性强。

水路运输；多港口挂靠；班轮运输；航线配船；数学模型

班轮公司在运输组织过程中必然要解决这样一个问题：如何配置班轮船队中不同类型的船舶到公司经营的各条航线上，使整个船队取得最佳的经济效益，即班轮航线配船问题。班轮航线配船决策应该满足两个基本要求：

1. 技术上可行，要求船舶的各项技术参数能够满足航线营运的条件。这可以根据客观因素及实际经验进行判断、解决。

2. 经济上合理、最有利。这是一个最优化问题，也是班轮航线配船的主要研究内容。

由于问题的复杂性，在实践中，一直是依靠投资经营者的个人经验和主观判断来进行班轮船队航线配船，缺乏科学、系统的决策分析方法。因此，从20世纪90年代起，国内外学者们开始对大型班轮船队进行航线配船和船队规划方面的探索，力求建立一套科学的数学方法和技术来解决这个问题。文献[1-2]探讨了更切合实际的航线配船非线性影响及其模型建立问题；文献[3]建立了适用于在同一航线上配置相同船型的典型班轮运输模式的班轮船队规划混合整数非线性规划模型。这些研究工作虽然在理论上取得了一些进展，做出了有益的探索，但由于模型解算复杂，在实用性上还存在一定的差距。

鉴于此，本文基于班轮运输组织方式的特点和要求，利用便于求解计算大规模问题的线性规划理论，研究、建立一个适于多港口挂靠班轮航线配船优化的数学模型，并通过算例对模型进行验证和分析。

1 问题描述与假设

针对一个具有一定规模的班轮船队，可通过货源调查和预测掌握研究期内其运营航线上任意港口间的货运需求量及运价水平。要求设计出最优的航线配船和发船班次方案，在技术可行的基础上，使班轮公司获得的经济效益最佳。

数学建模中采用的基本假设：

1. 研究期为一年、一个季度、一个月或其他单位时间。

2. 班轮公司经营的航线共G条，均为传统的多港口挂靠、货物直达运输航线，即船舶从起始港出发沿一个方向航行，中途可以挂靠多个港口，到达终点港卸完所有货物后重新装货，返回始发港，然后再进行下一个往返航次。[3]每艘船舶在去程和回程中都可以在多个中途港装、卸货物，并且不要求去程与回程必须访问相同的港口。

3. 班轮公司运营的航线网上挂靠港口总数为n，所有挂靠港口统一编号为1～n，每条航线上去程与回程的挂靠港口顺序确定。

4. 研究期内共有K种船型可供选择。

5. 各港口之间的货运需求量及运价水平已预测或确定。

6. 以集装箱量TEU为单位衡量船舶的承载能力和货运需求量，并且只考虑整箱装运，不考虑拼箱运输的情况。

7. 在两挂靠港口之间的往返运价不一定相同，即Fhij不一定等于Fhji。

8. 预先确定研究期内各型船在各航线上以最佳航速[4]航行时可以完成的往返航次数。

9. 为了提高服务质量，班轮公司会在经营的航线上保持稳定的班期，即规定研究期内航线的最小发船班次。

10. 船舶在给定航线上的往返航次成本不会因航次载货量变化而受到影响。

2 模型构建及求解

2.1数学模型

对于上述问题，以研究期内船队利润(总收入-航次营运成本)最大为目标，建立多港口挂靠班轮航线配船数学模型为

(1)

约束条件为

(2)

h=1,2,…,G;r=1,2,…,nph-1

(3)

h=1,2,…,G;r=1,2,…,ndh-1

(4)

(5)

(6)

xhij≥0h=1,2,…,G;i=1,2,…,n;

j=1,2,…,n

(7)

yhm≥0h=1,2,…,G;m=1,2,…,K

(8)

船舶航次营运成本Chm可由下式确定。[4]

(9)

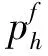
上述优化模型中，式(2)为货运量约束条件，要求研究期内船舶运输某种货物的总量不超过其货运需求量；式(3)和式(4)分别为每个挂靠港口正反两方向运输时船舶货运承载量约束[5-6]，船舶在任何港口装(卸)完货物驶向下一个港口时，船上所载货物总量不能超过其在此航线上的货运承载量(单船最大载货量与船舶在此航线上的平均装载率之积)；式(5)是对航线最小发船班次的约束，研究期内所有船舶在同一航线上完成的总航次数不能小于班轮公司要求的此航线最小发船班次；式(6)是对各型船数量的约束，研究期内用于运输的各型船数量之和不能大于船队中该型船的数量；式(7)和式(8)是决策变量非负约束。式(1)～式(8)构成了一个完整的混合整数线性规划模型。

2.2模型求解

分析表明，模型中有些变量和约束条件没有实际意义。例如，当i=j时，xhij为每个挂靠港向本港运输的集装箱数量；Vij为每个挂靠港到本港的集装箱运输需求量。在运用混合整数规划方法求解模型之前，可选择以下两种方式对这些变量和约束条件进行处理：

1) 在确定模型参数时，对于h航线上不能挂靠的港口对(i，j)，预先设定Fhij为一适当负值，可保证在最优解中h航线上船舶在(i，j)港口对间无运量发生，即xhij=0；在约束条件(2)中，对于所有航线都不能挂靠的港口对(i，j)，令Vij=0。

2) 从模型中将这些变量和约束条件消除。

采用第二种处理方式可减少模型的变量和约束条件，从而有效提高求解速度。

3 计算案例

3.1参数准备

某班轮公司经营3条沿海内贸集装箱航线，具体的航线图见图1。

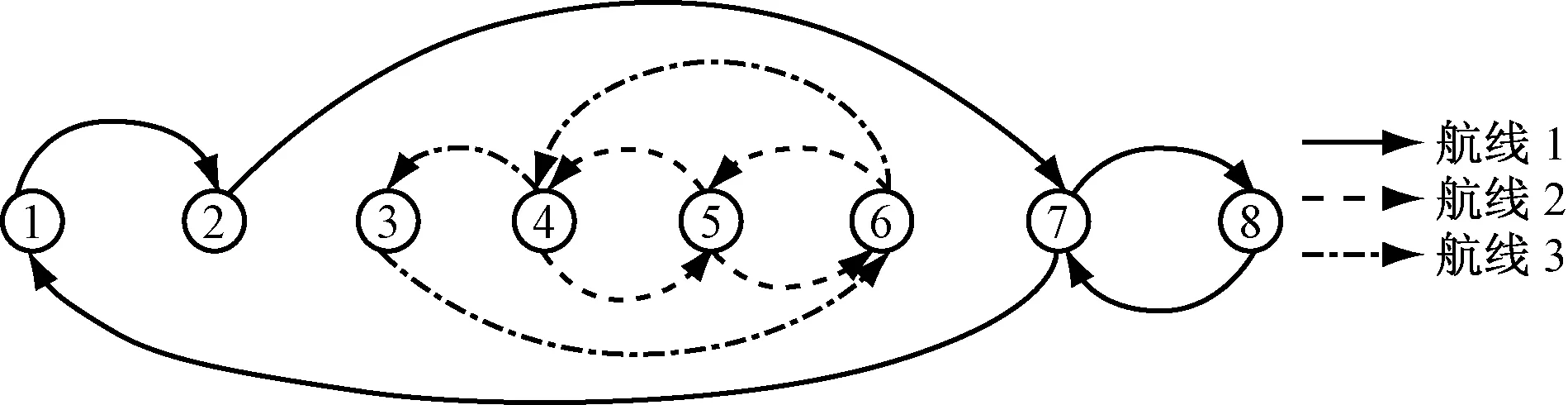
(注：1-天津，2-秦皇岛，3-大连，4-营口，5-烟台，6-上海，7-宁波，8-广州南沙)

设研究期为1 a，该班轮公司拥有的各型船舶数量及单船最大载货量见表1，为计算方便，本例中假设各型船在各航线上的平均载货率相同，取θ为0.7；研究期内各航线的挂靠港口及最小发船班次见表2；预测或确定的各挂靠港之间的货运需求量及运价见表3；各型船在各航线上的最大往返航次数及航次费用见表4。其中，由于客观条件限制，1型船不能在1航线上运营。

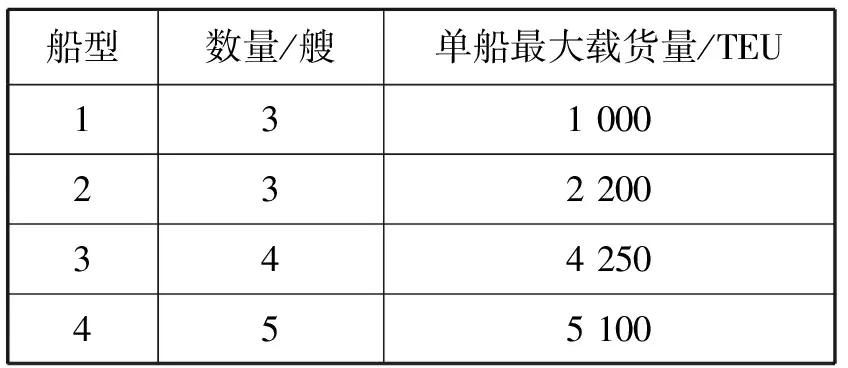
表1 各型船数量及单船最大载货量

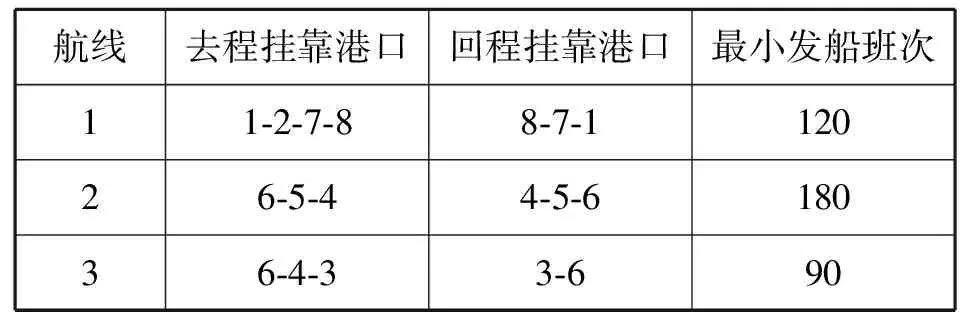
表2 研究期内各航线的挂靠港口及最小发船班次

3.2求解计算及结果分析

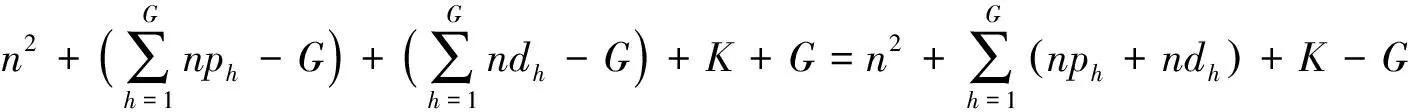
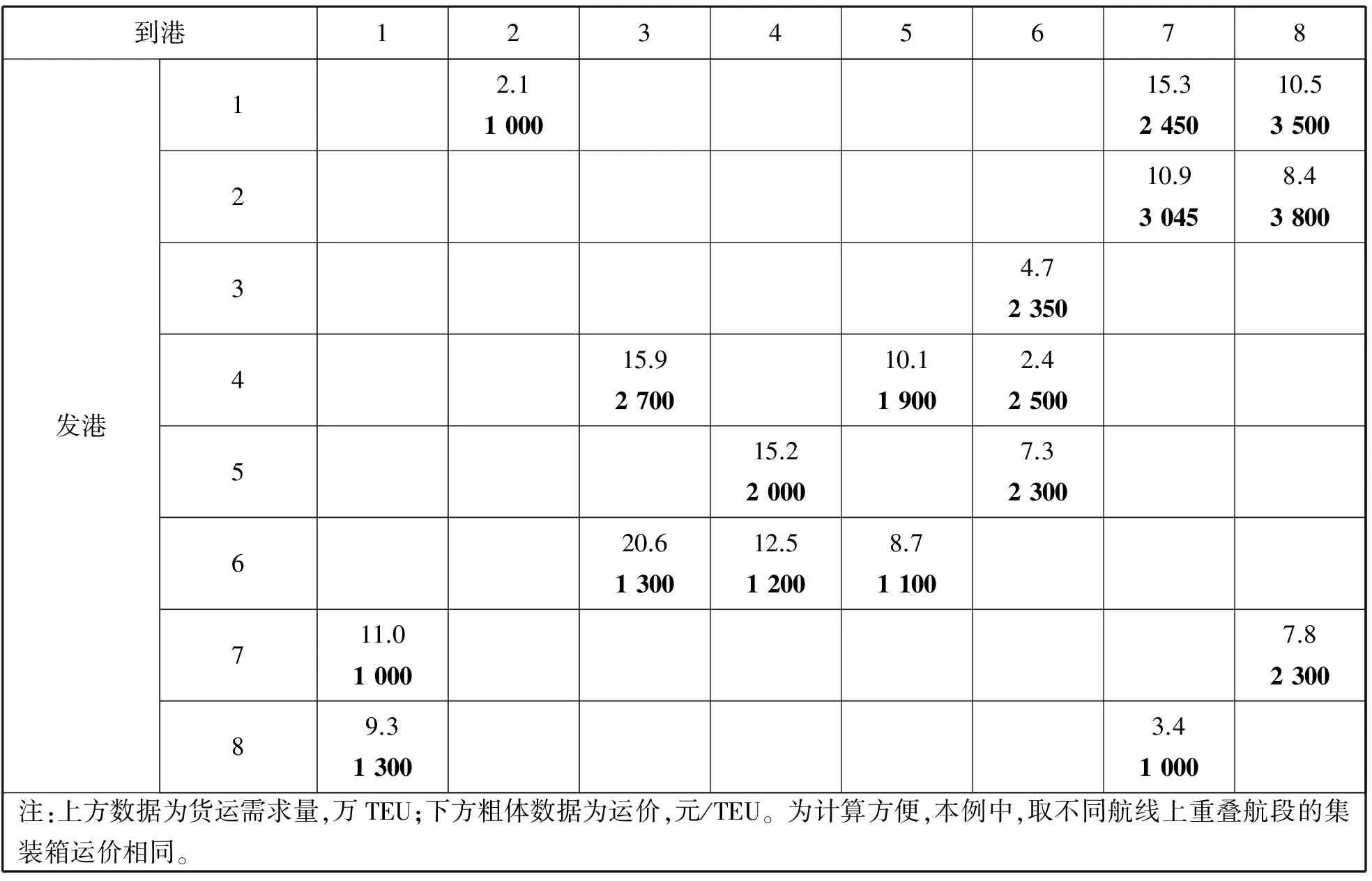
表3 研究期内各挂靠港之间货运需求量及运价

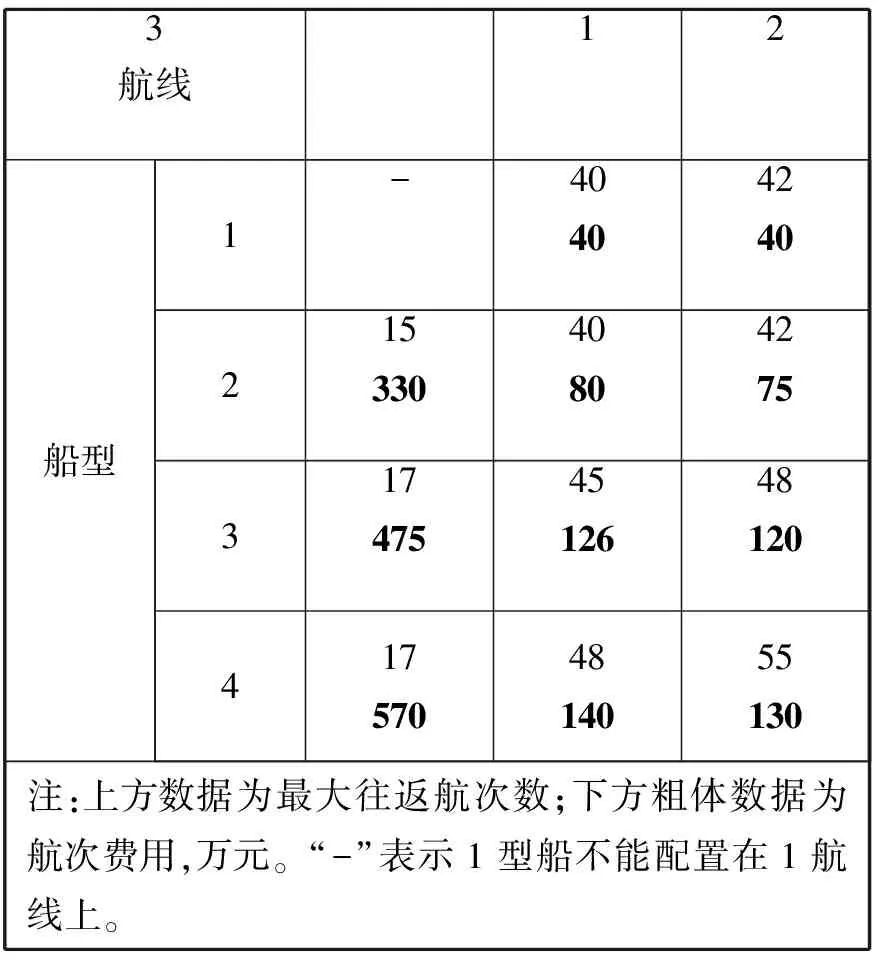
表4 研究期内各型船在各航线上的最大往返航次数及航次费用

y11(本算例中1型船不能配置在航线1上运营)；可以消除的约束条件包括式(2)中当i=j时对应的约束条件和(i，j)不是任何航线上的港口对时所对应的约束条件。算例中，在消除这类变量和约束条件后，有效变量为30个(见表5)，其中整数变量变为11个；有效约束条件为37个。消除这些变量和约束条件后，可大大提高模型的求解速度。

用上述混合整数线性规划模型求解该问题，得到的最优解见表5。按照表5的方案安排船队，除挂靠港1(天津)到挂靠港7(宁波)的部分货运需求外，该方案可满足表4中列出的各挂靠港间的运输需求。可验证计算结果能够保证式(2)～式(6)成立。得到的此优化计算结果(y值)是仅根据研究期内货运需求量确定的，而各航线上的具体发船间隔需根据货流分布特征进一步确定。

从优化结果的形式上看，本算例具有多个最优解，但各最优解的目标函数值(z值)及船队航线配船方案(y值)都相同(见表5)，区别仅在于挂靠港6(上海)到挂靠港4(营口)之间的货运量xhij不同。显然，当两挂靠港间的货物以不同航线运输但运价相同且船舶没有在所有港口都满载时，货流可能在不同航线(具有重叠航段)的船舶间适当转移，这种转移并不改变运输总收入和总成本，这是最优解不唯一的原因。这种最优解的多值性也表明，按照优化结果设置的航线配船方案对货流在一定范围内的变化具有适应性。

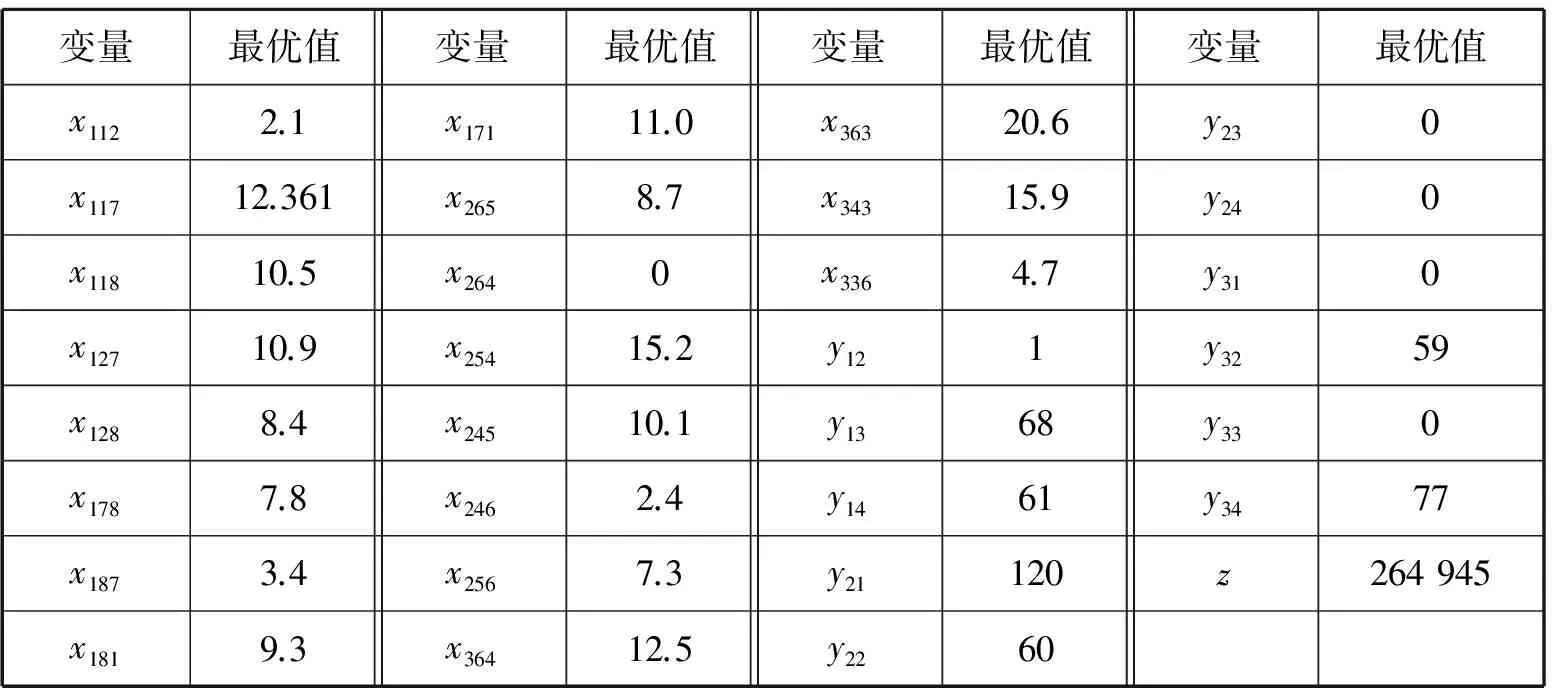
表5 最优解

表6 研究期内各型船平均闲置情况

4 结 语

根据班轮多港口挂靠与货物直达运输航线形式的特点，建立班轮航线配船混合整数线性优化模型。模型以追求研究期内班轮船队利润最大为目标，较全面地考虑货运需求、单船最大载货量、最小发船班次、运价水平等影响班轮航线配船的主要因素，更客观地反映了班轮运输组织的特征和规律。对于大型班轮船队，虽然模型的变量和约束条件较多、规模较大，但可以通过变量消减达到快速求解的目的。最后通过模拟和优化某班轮公司船队在研究期内的航线配船方案，验证提出模型的可行性，模型结构简洁、易于理解，且实用性强。

[1] XIE X，JI Z，YANG Y．Nonlinear Programming for Fleet Planning[J]．International Shipbuilding Progress，1993，40 (421)：93-103．

[2] 赵刚．班轮航线配船模型的分析与改进[J]．系统工程学报，1997，12(1)：80-86．

[3] 杨秋平，谢新连，裴光石．班轮运输船队规划模型与仿真[J]．西南交通大学学报，2011，46(6)：1046-1054．

[4] 谢新连．船舶运输管理与经营[M]．2版．大连：大连海事大学出版社，2009：189-195．

[5] 谢新连，王少成，杨秋平，等．一种公路客运线网优化设计方法[J]．大连海事大学学报，2009，35(4)：59-62．

[6] 王少成，凡亚军，杨秋平，等．大连市域内公路长途客运主要班车线网优化研究[J]．公路，2009(10)：171-175．

MathematicalModelofShip-RouteAllocationforMulti-CallLinerServiceanditsApplication

DUHong,XIEXinlian,TANGLei,ZHAOJiabao
(Integrated Transport Institute, Dalian Maritime University, Dalian 116026, China)

In order to meet the requirements of liner services with fixed schedules, and to optimize the liner shipping system, a mathematical optimization model for liner shipping allocation is established based on the multi-call liner route pattern, by comprehensively taking into account related factors, such as cargo demand, the capacity of a single ship, the minimum sail frequency and the tariff level. The objective of the model is to maximize the total profits of a liner fleet during an interested period. The modeling principle is introduced and the liner fleet of a shipping company is taken as an example to demonstrate the rationality of the model. The results indicate that the model correctly reflects the organization characteristics of liner shipping and optimizes the ship allocation and sail frequency. The form of the model is concise and easily understood, the solving process is fast and the model is very practical.

waterway transportation; multi-call; liner shipping; ship allocation; mathematical model

2014-01-02

高等学校博士学科点专项科研基金资助课题(20102125110002)

杜 红(1989-),女,山东潍坊人,硕士生,主要从事交通运输规划与管理方面的研究。E-mail:duhong.19890214@163.com.

1000-4653(2014)02-0113-05

F550；U692.3

A