供应船纵向加速度导数的估算方法

赵小仨, 罗 薇, 柯枭冰, 徐海祥

(武汉理工大学 a.高性能船舶技术教育部重点实验室； b.交通学院， 武汉 430063)

供应船纵向加速度导数的估算方法

赵小仨a,b, 罗 薇a,b, 柯枭冰a,b, 徐海祥a,b

(武汉理工大学 a.高性能船舶技术教育部重点实验室； b.交通学院， 武汉 430063)

由于作为海洋研究和开发的重要载体的供应船的控制技术决定着船舶能否按预定位置航行或停泊，因此，解决控制技术中的一个关键问题即确定船舶数学模型中的水动力导数很重要。采用CFD商用软件FLUENT，结合动网格技术，对系列供应船的纵荡运动进行数值模拟，得到系列船舶的纵向水动力，进而获得相应的纵向加速度导数，并分析数值计算结果的合理性。在此基础上，采用偏最小二乘的回归方法，得出供应船纵向加速度导数关于船型参数和呆木参数的估算公式。

水路运输；供应船；纵向加速度导数；数值计算；回归公式

在对海洋资源进行勘探开发的过程中，船舶或平台等海洋结构物经常需要固定于海洋中的特定位置进行作业。供应船[1]作为一种专门向船舶和海上设施运送物资的船舶，同样要求有一定的定点工作能力。为解决船舶位置和艏向的保持问题，基于动力定位的船舶控制技术[2]应运而生。其中，精确地计算船舶运动数学模型中的水动力导数是动力定位控制技术中的关键问题之一。因此，通过研究供应船的船型参数和呆木参数对水动力导数的影响，给出水动力导数的估算公式，为供应船控制系统的设计提供快捷、准确的数学模型参数，从而实现较精确的动力定位。

船舶有诸多水动力导数，国内外学者已对横向和艏摇方向水动力导数的计算做了大量工作。2008年国际专题研讨会SIMMAN 2008上提供了KVLCC1等船模纯横荡和纯艏摇运动的试验资料。邹早建等[3-5]通过求解非定常RANS方程，对KVLCC1裸船体的纯横荡和纯艏摇运动进行了数值模拟。刘山[6]用FINE-Marine软件模拟了DTMB5415的非定常纯横荡和纯艏摇运动。

目前,有关纵向水动力导数的研究还较少，特别是对于安装有艉呆木的供应船的研究。周昭明等[7-8]对日本著名的元良图谱进行多元回归,得到了纵向附加质量的估算公式,但其适用范围易受到限制，且预报精度难以保证。

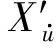
1 数值计算方法

1.1计算模型

计算模型的原型为一艘75 m供应船，缩尺比为1∶20。三维模型及其几何参数见图1和表1。

图1 三维船模

垂线间长/m船宽/m吃水/m方形系数3．40．8630．330．72

1.2坐标系

原点位于船中；X轴指向船首为正；Y轴指向左舷为正；Z轴正向依据右手定则。

1.3计算域和网格划分

选择计算域尺寸[3-6]：船首上游取1.5倍船长，船尾下游取3倍船长，船两侧取2倍船长，水深方向取8.3倍吃水。采用分块的方法，建全结构化网格。船体周围布置边界层，以提高计算精度。

1.4数值计算方法

1.4.1边界条件

入流面设为速度入口；出流面设为自由流出口；船体表面设为壁面无滑移；考虑到供应船在定位时低速航行，忽略自由面兴波影响，自由面设为对称面。

1.4.2定义动网格(Dynamic Mesh)

编写用户自定义函数(User Defined Feature,UDF)；网格更新方法选择网格光顺方法和动态层方法。

1.4.3离散格式和求解算法

空间离散采用二阶迎风差分格式；时间积分采用一阶隐式；求解算法采用SIMPLEC算法。

1.5计算工况

供应船在定点工作时属于低速、低频运动，拟采用线性操纵运动方程对其进行表达。基于以上思想，需保证船舶作低频微幅振荡。由于数值模拟不能直接计算出零频率下的水动力导数，因此分别模拟多个不同低频率时的纵荡运动，然后对频率进行线性拟合，最终得到零频率对应的水动力导数。

1.5.1选取纵荡频率[5,9]

综合已发表文章中的数值模拟实例与意大利罗马水池(INSEAN)的船模实验资料，此处的数值计算纵荡频率ω取为0.4 rad/s和0.3 rad/s。

1.5.2选取纵荡速度[10]

据第22届国际拖曳水池会议对船模PMM试验状态的选取建议，船模纵向速度Uc取0.6 m/s，u′取0.1。其中，u′为纵荡无因次纵向速度幅值，u′=ua/Uc。

1.6数据处理方案

1) 纯纵荡运动的条件

ψ=r=y=v=0

(1)

2) 运动的规律

(2)

式(2)中：a为纵荡幅值；ω为纵荡运动圆频率。

3) 基于线性假定，根据纯纵荡的运动规律，其水动力模型[11]可表示为

(3)

取FLUENT中计算稳定后的一个周期数据，在MATLAB中用最小二乘法拟合出各工况下的水动力函数关系，即得式(3)中的水动力导数，然后按式(4)进行无因次化，随后再把各个频率的无因次化水动力导数线性拟合至零频率。

(4)

1.7数值计算方法验证

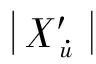
图2 长椭球体网格图

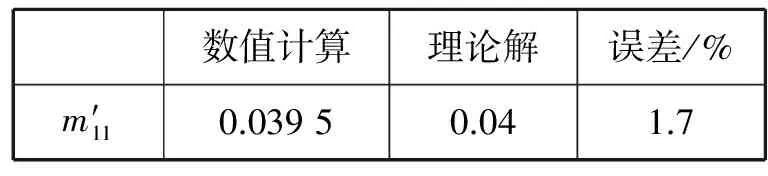
数值计算理论解误差/%m′110．03950．041．7

2 数值计算结果及公式回归

根据供应船实船资料，统计出船舶主尺度变化范围(见表3)，其中:L为垂线间长；B为船宽；d为吃水；Cb为方形系数；Am为呆木侧投影面积。

表3 供应船的船型参数变化范围

2.1系列船型变换方案

为减小尺度效应造成的误差，变换船型过程中保证排水量Δ不变，采用L/B与Cb交叉组合的方式派生出符合要求的16条新船型，其他船型参数作为被动变量。船型变换方案见图3。

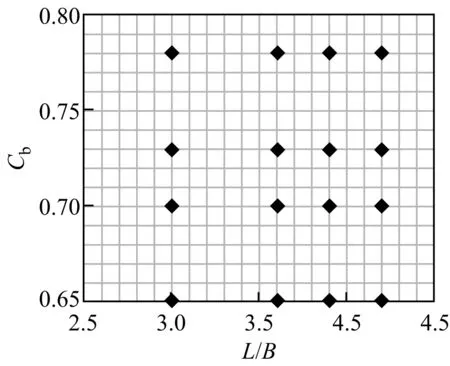
图3 供应船的系列船型变换

2.2系列呆木变换方案

系列呆木变换中的自变量为呆木侧投影面积Am。此处保持船型及呆木斜度θ不变，固定住呆木前端，把呆木后端分别向前或向后平移，派生出新呆木F1，F2和F4，母型船呆木记为F3，则系列呆木变换见图4。

2.3计算结果与分析

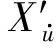
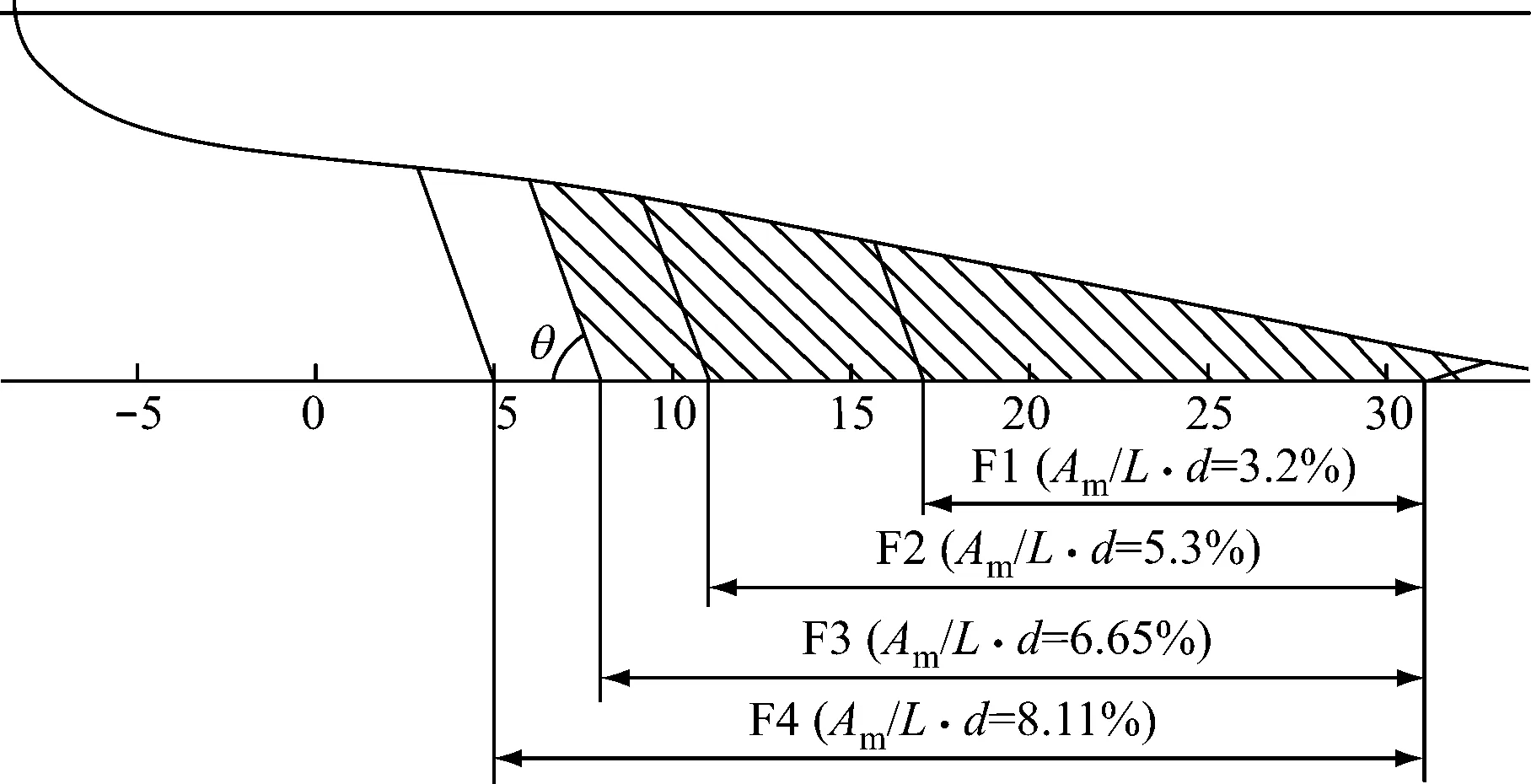
图4 系列呆木变换

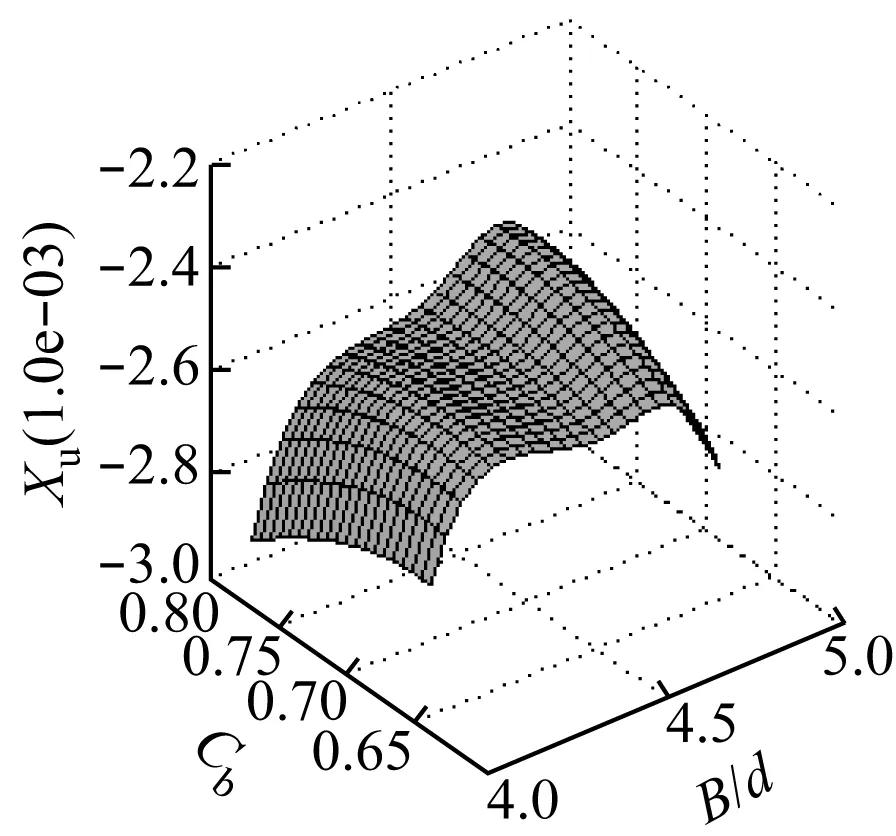
图5 无因次纵向加速度导数随船型参数的变化

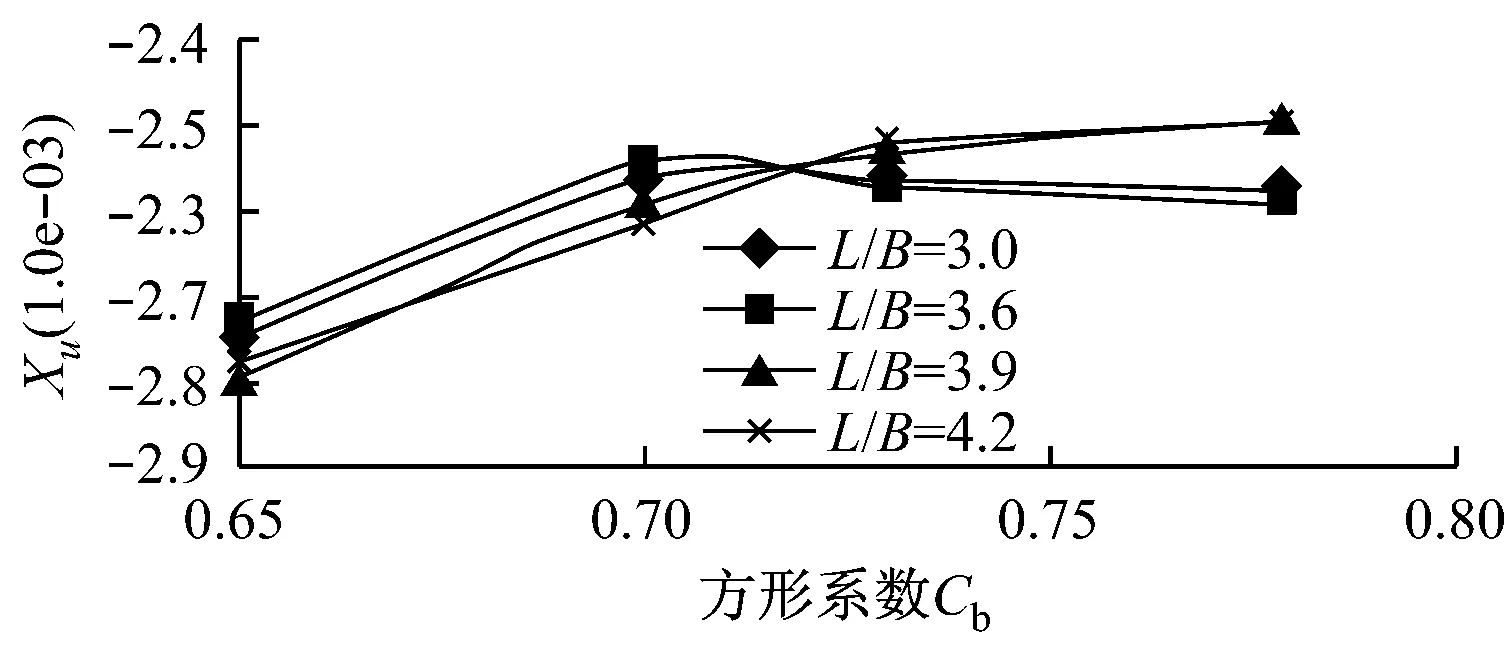
图6 零频率时随Cb的变化

表4 零频率时系列呆木的值

2.4纵向加速度导数的多元回归

水动力导数一般主要与船型参数L，B，d，Cb有关，取水动力导数的无因次量为因变量，船型参数的无因次量以及二次耦合量为自变量。由于研究对象为带有呆木的供应船，因此自变量需加上呆木面积的无因次量。

[8]和[13]中的回归公式，可假设水动力导数与船型参数之间的关系为线性的。把自变量记为xi(i=1,2,…)，建立回归模型为

(5)

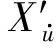
(6)

式(6)的适用范围为：船型参数在表5统计范围内的供应船。为考察回归模型的精度，绘制样本点预测图(见图7)。从图7中可看出，观测值与预测值拟合效果较好。残差平方和为4.1e-8，调整判定系数R2为0.997。

图7 水动力导数的预测图

为直观、迅速地观察各个自变量对因变量的解释能力，绘制变量投影重要性指标图[4](Variable Importance in Projection, VIP)。图8表示置信度取为95%的VIP图。可看出前5个自变量的VIP值超过1，说明其在解释因变量时起到了比较重要的作用。总体上各自变量的VIP值均在0.5以上，进一步说明自变量集合的选取较合理。

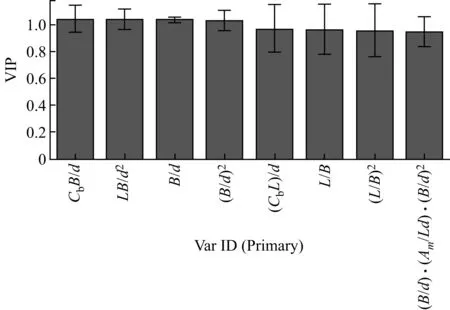
图8 变量投影重要性指标VIP

3 结 语

参考文献

[1] 林洪波.供应船的稳性特点[J].天津航海,1987(3):27-29.

[2] 边信黔,付明玉,王元慧.船舶动力定位[M].北京：科学出版社,2011：118-201.

[3] 邹早建,杨勇,张晨曦.深浅水中KVLCC船体横荡运动水动力数值计算[J].水动力学研究与进展,2011,26(1):85-92.

[4] 杨勇,邹早建,楼鹏宇.小振幅平面运动机构试验黏性流场数值模拟[C].第二十三届全国水动力学研讨会第十届全国水动力学学术会议文集,2011.

[5] 杨勇.非定常操纵运动船体水动力数值计算[D].上海：上海交通大学,2011.

[6] 刘山.基于CFD技术数值模拟平面运动机构试验[D].武汉：武汉理工大学,2012.

[7] 周昭明,盛子寅,冯悟时.多用途货船的操纵性预报计算[J].船舶工程,1983(6):21-31.

[8] 贾欣乐，杨盐生.船舶运动数学模型-机理建模与辨识建模[M].大连:大连海事大学出版社,1999:146.

[9] 姜哲,石珣,王磊.动力定位船舶水动力参数数值试验研究[J].实验室研究与探索,2005,24(12):14-17.

[10] VANTORRE M. Captive Manoeuvring Tests with Ship Models: A Review of Actual Practice, Based on the 22nd ITTC Manoeuvring Committee Questionnaire[D]. Ghent: University of Ghent, Ghent.

[11] 盛振邦,刘应中.船舶原理(下)[M].上海:上海交通大学出版社,2004:280-284.

[12] 吴秀恒,张乐文,王仁康.船舶操纵性与耐波性[M].人民交通出版社,1988:123-128.

[13] 杨盐生,于晓利.低速域船体流体动力的实用估算法[J].大连海事大学学报, 1998,24(2):6-10.

[14] 李世玲.基于PLS成分的变量筛选法[J].信息与电子工程, 2003,1(2):31-35.

[15] 王惠文,吴载斌,孟洁.偏最小二乘回归的线性与非线性方法[M].北京：国防工业出版社,2006:279-307.

MethodforEstimatingLongitudinalAccelerationDerivativesofSupplyVessels

ZHAOXiaosaa,b,LUOWeia,b,KEXiaobinga,b,XUHaixianga,b

(a. Key Laboratory of High Performance Ship Technology of Ministry of Education; b. School of Transportation, Wuhan University of Technology, Wuhan 430063, China)

The accuracy of ship model parameters is of critical importance to oceanographic research support ships which need motion control to move or stop according to given plan. The dynamic characteristics of a series of oceanographic research support ships are studied through numerical simulation of surge motion of ships, using commercial CFD software FLUENT and dynamic mesh technology. The hydrodynamic longitudinal derivatives of the ships are determined in the process. After the rationality of the results of the numerical calculation has been checked, the formula relating the ship longitudinal acceleration derivative to ship hull form and deadwood parameters are obtained by partial least square regression method.

waterway transportation; supply vessel; longitudinal acceleration derivative; numerical calculation; regression formula

2014-08-11

赵小仨(1989—), 女, 湖北襄阳人，硕士，研究方向为船舶水动力。E-mail:741504374@qq.com

1000-4653(2014)04-0088-04

U661

A