宏程序嵌套编程在数控铣削加工中的应用

郑向周 杨 冰



宏程序嵌套编程在数控铣削加工中的应用

郑向周 杨 冰

(运城职业技术学院机电工程系 山西运城 044000)

宏程序是数控编程的高级语言。用户宏程序通过数控系统对变量进行算术运算、逻辑运算和函数的混合运算，再通过条件循环语句以及程序嵌套的综合运用，可以用较少的编程语句完成较大的编程工作，减少了手工编程时繁琐的数值计算。实现了椭圆、抛物线、双曲线等曲线编程，又能通过参数改变进行零件形状的改变，充分发挥了数控机床智能、高效、柔性、自动化的特点，扩展了其应用范围。

宏程序 铣削加工 倒角 椭圆

机械零件边缘轮廓根据需要经常设计成倒棱或圆角形状。回转类工件在车床上进行倒(圆)角加工是容易实现的，非回转形状的倒(圆)角可以在数控镗铣床上进行加工。对于轮廓形状比较简单、手工编程容易实现的形状，可以用倒(圆)角成型刀具进行加工，但需要准备不同类型的刀具，其成本较大且不具备柔性加工能力。也可以借助CAD/CAM软件进行自动编程[1]，实现轮廓插补功能，但程序冗长且效率不高。以下就尝试用宏程序变半径补偿及嵌套功能的编程方法实现任意形状的倒(圆)角加工。

1 用球头铣刀加工任意圆角及倒角的方法

在数控铣床上进行倒(圆)角实际上是一种两轴半加工，通过刀具切削深度的变化实现层加工，刀具半径补偿值的变化实现所要求的倒(圆)角形状拟合，其刀具轨迹类似地图中的等高线。华中数控系统对于半径补偿设置有两种方法，可以在刀补表中设立刀补半径值，通过G41或G42的调用实现，适用于刀具半径补偿值不变的状态；也可以用#100～#199全局变量来定义半径补偿量[2]，赋值与变量，使其在循环中变化，实现刀具半径补偿的不断改变，从而改变刀具的径向加工轨迹。以下推导使用球头铣刀加工倒(圆)角时，刀具切削位置和变量之间的数学逻辑关系。

1.1 圆角的加工

如图1所示，要将圆弧加工出来，刀具从位置运动到位置。设所加工圆角半径值，刀具半径，得到刀具深度切削值随变量变化关系为：

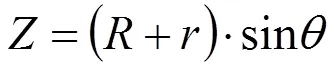
在圆角底部刀具半径补偿值为，在顶部刀补值为-, 得到刀具半径补偿随变量变化关系式为：

从0°增加至90°可以将圆角拟合加工完成。

数控系统循环语句的格式为：

运用到本例，程序如下：

1.2 倒角的加工

如图2所示，加工的倒角尺寸高,角度。铣刀刀位点在球头圆心处。在起刀位置，铣刀与倒角延长线相切。

图2 倒角的加工

根据几何关系得到铣刀刀位点1尺寸：

设上平面为零面，终止位置高度尺寸2:

2=· cos

工件上平面定位零位置，设铣刀层升高变量值，得到刀具切削高度随变量的变化关系：

=(1-)+

起始位置刀补半径值为，抬刀则刀补半径缩小/tan,随变量变化规律：

#101=-/tan

运用宏程序循环语句得到程序如下：

2 宏程序加工椭圆方法

数控编程未对椭圆、抛物线等数学可表达曲线提供编程指令，但是利用宏程序功能能够实现对这些曲线轮廓插补的功能。以下给出椭圆宏程序编程方法，其他曲线编程方法类同。

3 用宏程序嵌套方法加工斜椭圆倒圆角

如图3所示，轮廓的倒圆角，椭圆长半轴35，短半轴20，顺转45°。通过循环嵌套的使用，椭圆插补程序为内循环，倒圆角为外循环，实现层叠加工将圆角拟合而成。

图3 倾斜 45°的椭圆

如图4所示，采用普通平底铣刀进行加工。刀具的刀位点为刀具中心，刀尖从位置运动到位置，得到刀具切削深度公式：

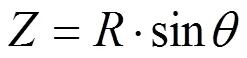
刀补半径补偿起始值为，层加工到位置时可以看出向加工方向靠近(-·cos)，所以刀补半径值的变化式：

#101=-(-·cos)

本例用12铣刀加工5圆角，完整的应用程序如下：

%0001

N10 G00 G40 G49 G5400100

N20 M03 S500 M07

N30 G6800 P45

N4040

N5060-60

N60 G01-5 F100

N70 #1=6；刀具半径

N80 #2=5；圆角半径

N90 #3=0；圆弧拟合初始角0°

N100 WHILE #3 LE 90；圆角加工外循环开始

N110 G01 Z[#2*SIN[#3*PI/180]-#2]；定刀具深度

N120 #101=#1-[#2-#2*COS[#3*PI/180]]；变刀补半径

N130 G0135 G42 D101；加刀补

N1400

N150 #4=0；椭圆步距角初始值0

N160 #5=35；椭圆长半轴

N170 #6=20；椭圆短半轴

N180 WHILE #4 LE 360；椭圆插补内循环开始

N190 G01X[#5*COS[#4*PI/180]]

Y[#6*SIN[#4*PI/180]](按参数方程进行轮廓插补)

N200 #4=#4+1；椭圆插补步距角为1°

N210 ENDW；内循环结束

N220 #3=#3+3；圆弧拟合步距角3°

N230 ENDW；外循环结束

N240 G0050

N25000 G40

N260 G69

N270 M05 M30

4 结语

通过用宏程序完成倒(圆)角编程的阐述，并以旋转45°椭圆形状倒圆角为例进行了讲解，充分利用了数控铣削功能指令。参数化编程作为手工编程的扩充，增强了零件加工程序的可读性与灵活性，扩展了数控系统的使用功能[3]，为解决一些特殊结构零件的加工提供了一种新的思路。

[1] 倪春杰.变半径补偿宏程序在轮廓倒圆角中的应用[J]. 兰州石化职业技术学院学报,2009,9(2):19-20.

[2] 武汉华中数控股份有限公司.世纪星铣床数控系统编程说明书[Z].2009.

[3] 卢培文.参数化编程在数控铣削中轮廓倒圆角的应用[J].金属加工,2008(2):37-38.