变电构架温度应力计算
刘安禄,孙谋成
(1.东北电力设计院,长春 130021;2.国网本溪供电公司,辽宁 本溪 117000)
连续多跨变电构架和双向联合构架具有足够的侧向刚度,端撑构架和刚架结构具有很高的抗侧向荷载能力和抗变形刚度,但在构架正常使用与构架安装温度不同时,产生了构架温度应力。本文通过常用的人字柱变电构架温度应力分析,提出解决温度应力计算的基本方法和思路。
1 带端撑的变电构架温度应力计算
1.1 建立计算模型
在单位荷载作用下,中间柱的侧向刚度是端撑的(1/80~1/120),所以假定梁的伸缩温度应力全由两个端撑承担,当温度升高(降低)时,端撑推力等于梁的压缩力,考虑端撑销钉及梁柱连接螺栓松动变形损失后,梁的总变形量是梁的温度伸长(缩短)变形与有端撑边柱的推力(拉伸)变形之和,构架最后变形为:梁的温度力变形与柱顶推移变形之和等于梁的温度变形与梁柱连接螺栓松动变形损失值之差。
设温度应力为pW,则计算公式为:
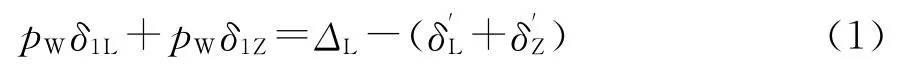
式(1)整理简化后为:

1.2 采用虚功原理计算构架杆件弹性变形
梁的单位力变形计算公式为:

式中:N1为虚拟单位力产生的轴力;NP为外荷载;L为梁总长的1/2;E为钢的弹性模量,E=2.06×105;A为钢管梁截面面积,或桁架梁下弦面积(下弦两主材)。
N1=NP=1,式(3)整理简化后为:

边柱的单位力变形计算公式为:

式中:h为柱高,端撑斜长≈h;b为端撑跟开(人字外);AD为端撑钢管面积;AB为边柱(肢)钢管面积。
因为单位力与外力相等,N1=Np,N1Np=≈(h/b)2,设端撑钢管面积/边柱(肢)钢管面积k=AD/AB,式(5)简化为δ1Z=(2+k)/2k×(EAB),考虑到边柱的弯矩变形,上式再乘1.1增大系数,则:δ1Z=1.1(2+k)/2k×,通常端撑与边柱面积基本相同,即K≈1,式(5)简化为:

1.3 梁的温度变形计算
梁的温度变形计算公式为:

式中:α为钢的线膨胀系数,α=1.2×10-5;Δt为设计温差,与大风组合,根据DL/T 5457《变电站建筑结构设计技术规程》规定,Δt=35℃。对于我国新疆、内蒙古、东北等高寒或寒冷地区,根据实际环境条件,Δt可酌情放大。
1.4 梁柱的变形损失值计算
梁柱的变形损失值,应按实测资料计算,在没有足够实测资料之前,可按桁架变位的经验来推算,工程实践表明,按《电力工程高压送电线路设计手册》(以下简称手册)(6-5-3)式计算,桁架梁斜材螺栓松动变形实测值大于计算值约1.5倍,原因是主斜材单螺栓连接孔壁挤压塑性变形较大,局部受力较大杆件,比如梁柱支座斜材销钉与孔壁的间隙e值可达2.5mm。
a.边柱变形损失值。带端撑的人字柱,边柱销钉松动变形,销钉与孔壁的间隙为2~4 mm,因销钉直径较大(多在60~80 mm),孔壁又宽,无挤压变形,取销钉孔间隙e平均值偏下2.5mm(施工图中销钉孔间隙不宜过大),考虑取松动的一半,所以再除以2。边柱的变形损失值计算公式:

式中:e=2.5 mm;n为每个杆件两头连接点数量,一般为2,但边柱端撑与基础端无螺栓连接,所以n=1;N1=h/b为杆件数,边柱只有拉压两杆(边柱2AB算一件),总共2件=2。
式(8)简化整理后:

b.梁的变形损失值。分梁支座柱连接及桁架梁下弦主材连接两部分,构架梁支座与柱的连接形式通常有3 种:角钢桁架梁端部与柱头连接(见图1a),钢管桁架梁与柱头连接(见图1b),单钢管与柱头法兰连接(见图1c)。角钢桁架梁端部与柱头连接螺栓,220kV 以下桁架梁多为单排连接;500kV及以上采用钢管桁架梁时,每根钢管主材用4个螺栓,剪切集中受力;最大设计风速时连续构架两端连接螺栓容易产生塑性挤压变形,螺栓间隙e可取2.0mm 以上,对于单钢管与柱头法兰连接,基本不存在螺栓拉压的塑性变形。
桁架梁下主材角钢(内外包)连接出现温度应力之前,螺栓孔隙变形已经基本完成,再加温度拉应力,松动变形很小。桁架梁下主材钢管连接松动变形更小,为了简化计算,所有桁架梁下主材变形损可失忽略不计,桁架梁变形损失,考虑全部集中在梁支座与柱连接的孔壁挤压应力上,温度应力略占不同梁长(电压等级)大风工况水平力的15%~30%,可按受力大小,取不同螺栓间隙e值来计算梁的变形损失值。
桁架梁两端柱头连接螺栓孔隙变形损失,由于梁的长度差别较大,按电压等级分为220kV 及以下,500kV 及1 000kV3种,梁长度分别为13、27、54m,计算温差取Δt=35℃,其弹性变形分别为5.46、11.34、22.68mm,梁支座螺孔间隙e 按传递的水平力大小分别取1.5、2.0、2.5 mm,则梁的变形损失为0.27L、0.17L 及0.11L,简化取整为0.3L、0.2L、0.1L(对应的e 值为1.7、2.2、2.3 mm)。
综合以上分析,有端撑构架梁柱变形损失δ′=
角钢或钢管桁架梁的构架变形损失为:


图1 构架梁支座与柱的连接形式
钢管梁与柱头法兰连接的构架变形损失为:

式中:n梁跨13m 及以下取0.3,27m 取0.2,54m取0.1,带入式(2)并整理后,有端撑构架的温度应力作用为:

式中:m 是桁架梁的温度应力损失数。单钢管梁与柱头法兰连接的构架m 取1.0;通过剪切螺栓与柱头连接的桁架梁,跨长13m 及以下时m 取0.7;跨长27m 时m 取0.8;跨长54m 时m 取0.9。
按以上思路,以下3种情况,220kV10跨13m长角钢桁架梁、220kV 构架5 跨24 m 长钢管梁、1 000kV4跨54m 长桁架角钢梁,温度应力计值分别为20.3、44.2、68.9kN。
2 不带端撑的变电构架温度应力计算
2.1 计算模型
近几年工程在220kV 构架中常用单钢管梁与人字柱组成刚架结构无端撑连续构架,构架梁柱连接采用法兰对接,温度应力基本不存在损失(横梁纵向温度拉压应力为5~10N/mm2),这种连续刚架结构计算适合采用有限元位移法,具体步骤如下。
两端固结杆件(设杆端为A 及B)单位侧移杆端内力,也可称为固端滑动弯矩:

式中:E为构架柱的弹性模量;I为构架柱的惯性矩(人字柱是双柱,用2EI);H为构架柱计算长度。
按公式(7)计算整排构架梁长一半的温度变形Δn,Δn=αΔtLn。刚架两端最大温度应力侧移弯矩Mn=6EIΔn/H2,倒数第2柱弯矩Mn-1=Δn-16EI/H2,n为整排构架一半的跨数,Δ1为单跨梁的温度变形,Δ1=Δn/n,Δn-1=Δn-Δ1。
将Mn,Mn-1当外荷载作用在端柱和倒数第2根柱的上下两端,端柱有最大温度应力,但导线张力只有1根半,倒数第2根柱,温度应力较小,但导线张力是3根,柱截面计算选用两者中较大值。
2.2 应用举例
66kV 钢管人字柱构架连续7跨梁柱固结,梁跨13m(每跨前后6根导线风压)柱子2φ300mm×6mm,高9m,构架示意图见图2。

图2 7跨66 kV固结钢管构架示意图
梁的温度变形Δ3.5计算:α=1.2×10-5;Δt=35℃;L3.5=91 000mm/2=45 500mm
Δ3.5=αΔtL3.5=19.11mm
最后一根柱端弯矩计算:Δ3.5=19.11mm;E=2.06×105;H=9 000mm;I=119.8×106。
M3.5=Δ3.56EI/H2;=34.93kN·m
倒数第2根柱的柱顶变位值计算:
Δ1=Δ3.5/n=5.46mm
Δ2.5=Δ3.5-Δ1=13.65mm
M2.5=Δ2.56EI/H2=24.92×106kN·m
将此柱顶柱底弯矩反向,以节点荷载施加到结构计算模型中,进行结构内力计算与分析,当与大风组合时,还需要再乘荷载组合系数0.85。
3 结论
a.当连续多跨变电构架两端设有端撑时,作用在梁及端撑上的温度应力计算公式为:

b.不带端撑梁柱固结变电构架的温度应力计算公式为:最后一根端柱温度应力Mn=Δn6EI/H2;倒数第二根柱温度应力Mn-1=Δn-16EI/H2。将Mn,Mn-1当外荷载分别加在最后一根端柱及倒数第二根柱的上下端,与大风工况组合后取较大值。
c.温度应力效与大风组合时,须乘荷载组合系数0.85。
以上构架温度应力的计算方法,是基于目前工程中常规设计方案进行分析,总体上仍偏于安全,当构架出现特殊的构造时,还应针对具体构造进行具体分析。

