高铁列车移动荷载对下穿隧道影响的数值分析
巫裕斌,张梦楠,漆泰岳,李 延
(1.西南交通大学交通隧道工程教育部重点实验室,四川成都 610031;2.西南交通大学土木工程学院,四川 成都 610031)
随着我国铁路和城市轨道交通建设的飞速发展,不同交通形式的空间交叉问题将会越来越多,地铁隧道下穿既有铁路的情况也会越来越常见,高速列车正常的运行以及地铁隧道下穿过程中的安全等问题也会越来越突出。其中,关于加固方案和沉降控制的研究成果较多,徐干成等[1]通过数值模拟认为对下穿段一定范围内土体进行注浆加固可以有效地控制既有铁路的沉降;霍军帅等[2]分析了板桩组合结构加固方案的适用性;许恺等[3]分析了列车速度对地铁施工和地表沉降的影响并提出合理的列车限速值。
地铁建成投入运营后,地表高铁列车通过时仍然对该下穿段地铁的围岩和隧道结构产生影响。根据《高速铁路设计规范(试行)》,列车荷载采用拟静力法进行简化,即在静荷载作用的基础上乘以一个放大系数用来模拟动荷载。但是根据目前的发展状况,高速铁路列车速度越来越快,拟静力法的适用性越来越差。因此,越来越多的学者开始研究移动荷载对地基的影响。张学钢等[4]研究了地铁移动荷载作用下软土地基的沉降特性并进行了动力分析;张玉娥等[5]根据现场试验得出列车激振荷载表达式。本文以实际工程为背景,采用MIDAS/GTS建立地铁隧道下穿高速铁路路基的有限元模型进行动力分析,分析高铁列车以不同速度通过时对地表的动力响应和变形情况,通过对比分析给出列车通过该段的建议时速。
1 工程概况
广州某地铁下穿广州火车北站段,区间隧道采用盾构法施工。盾构穿越铁路下方隧道长度约100 m,其间下穿武广客专2条股道,隧道与轨道间的平面夹角大致为70°,其位置关系如图1。下穿段地铁区间隧道埋深约为7.8~9.0 m。为满足工后沉降需求,对区间隧道上方一定范围进行注浆加固,加固区域宽23.5 m,高4.5 m,其顶部距地表4 m。注浆孔布置为纵向间距6 m,排距6 m,梅花形布置。根据武广客专广州北站部分地质钻孔资料,该地段地貌上属于河流冲洪积平原,地势平坦宽广,局部为剥蚀垄状残丘,揭露第四系地层为人工填土,冲洪积砂层和黏性土层及残积层,基岩为石炭系灰岩。
广州北站作为武广客专的中途站,绝大部分列车将按照设计速度约300 km/h越行通过。而路基、轨道平整度直接影响高速铁路运营安全,加之下穿浅埋地铁盾构隧道条件复杂,有必要先通过数值模拟的方法对列车通过速度对路基、地铁隧道的影响以及该设计通过速度是否合理进行讨论。
2 数值模型建立
本文使用MIDAS/GTS建立该下穿段的三维有限元模型。建模过程中做如下几点考虑:
1)轨道板、支撑层视为一个整体,轨道板、土体、注浆体采用实体单元模拟,采用摩尔—库伦屈服准则;管片通过析取隧道单元获得,视为弹性单元。
2)列车移动荷载简化为作用在轨道板中心线上随时间变化的均布荷载,假设两轨道板上列车荷载移动方向相同,即模拟两列车同向通过时的情况,列车通过速度分别取80,120,200 和300 km/h。
3)日本《板式轨道用路基结构设计、施工手册》中规定,新干线采用的路基挠曲量为L/1600(L为按照简支梁的挠曲假设时的假设跨度),挠曲曲面为半正弦波形。根据此规定,当L=20 m时,其不均匀沉降控制标准为 12.5 mm/20 m[6]。
德国铁路技术规范对路基沉降量也作出了相应的规定。对于无砟轨道工后总沉降SR不允许超过最大调整量减去5 mm,当路基长度>20 m且为均匀沉降时,可以将工后沉降量提高为折减调整量的2倍,控制标准为30 mm/20 m,其中扣除的5 mm是预留的由通车后列车荷载引起的常规基础沉降[7]。
我国《高速铁路设计规范(试行)》及《新建时速300~350公里客运专线铁路设计暂行规定》规定,无砟轨道路基工后沉降一般不应超过扣件允许调整的沉降调高量15 mm。对于长度>20 m且均匀沉降的路基,如果调整轨面高程后(轨面为圆顺的竖曲线),允许将最大工后沉降调至30 mm[8]。
在已有下穿工程中,北京地铁14号线区间盾构隧道下穿京津城际高速铁路的路基沉降控制标准为15 mm。由于下穿浅埋隧道工程实例较少并且本文进行动力分析,工程条件相对复杂,结合上述数据并参考国内外相关条文规范,拟定路基沉降控制标准为20 mm。
2.1 几何尺寸拟定
模型拟采用尺寸:宽×高×长=60 m×90 m×25 m。圆形隧道半径为3 m,衬砌厚度为0.3 m,拱顶距地表9 m;左右线间距为12 m,距模型边界均为18 m;轨道板宽×高=2.8 m×0.24 m。
2.2 力学参数拟定
根据该段岩土地质勘察报告,模型计算所需材料的力学参数如表1所示[9]。表中土层分布按照从地表向下的顺序排列。
2.3 荷载拟定
在缺乏现场实测数据的情况下,参考现有的研究成果及相关试验结论,主要根据参考文献[10]确定列车激振荷载表达式为
式中:P0为列车车轮静载;Pi为相应频率的震动荷载幅值,Pi=M0αiω2i,M0为列车簧下质量,αi为相应于不平稳控制条件下的几何不平顺矢高(钢轨基本振动振幅),ωi为振动圆频率,ωi=2πvi/L,vi为列车的行车速度,L为钢轨几何不平顺曲线的波长。
取单边静轮载 P0为125 kN,簧下质量 M0为750 kg,矢高αi为14 mm,波长L为2 m。以列车通过速度v=80 km/h为例,由式(1)求得列车荷载前10 s的列车激振荷载的时程曲线如图2所示。
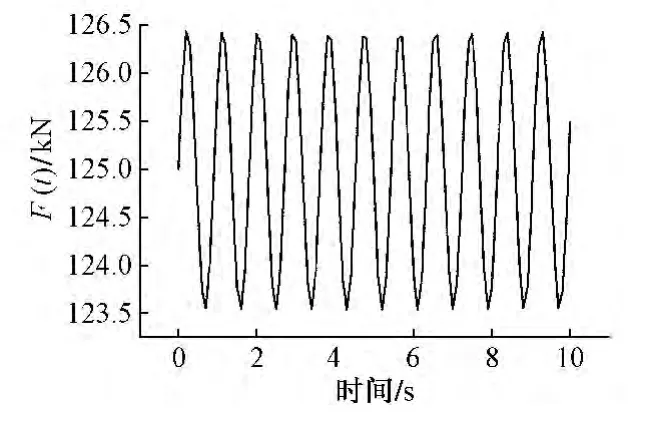
图2 列车荷载时程曲线(v=80 km/h)
2.4 约束条件拟定
根据动力计算相关理论,首先要先计算模型的特征值,然后选择模态较大的频率作为基准计算模型的瑞利阻尼系数。因此,用弹性吸收边界模拟模型约束条件。约束边界计算公式如下[11-12]
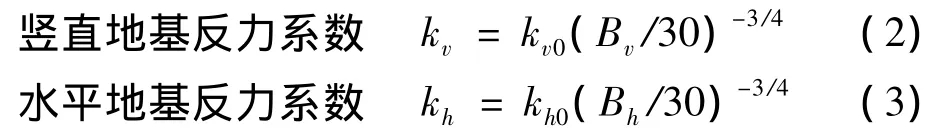

3 计算结果
列车高速通过必然会引起地表及以下一定范围内土层的振动而产生变形,并且有可能影响隧道结构和高铁行车安全,有必要关注沿轨道板轴线地表的最大沉降和地铁隧道拱顶的最大位移以及动力响应。
3.1 最大位移
列车通过后地表沉降的最大位置均位于模型地表中部轨道板沿线上。v=80 km/h时,轨道板下方路基最大沉降值为18.5 mm;v=120 km/h时,最大沉降值为20.4 mm;v=200 km/h时,最大沉降值为26.5 mm;v=300 km/h时,最大沉降值为28.8 mm。根据本文前述所拟定的沉降标准,当列车速度>200 km/h时沉降值已超限。列车高速通过下穿段时会造成地表部分区域隆起,当车速为300 km/h时,隆起的区域距离轨道板较近,隆起最大值为19.2 mm。
列车以不同速度通过时沿轨道板轴线方向地表的最大总沉降如图3所示。
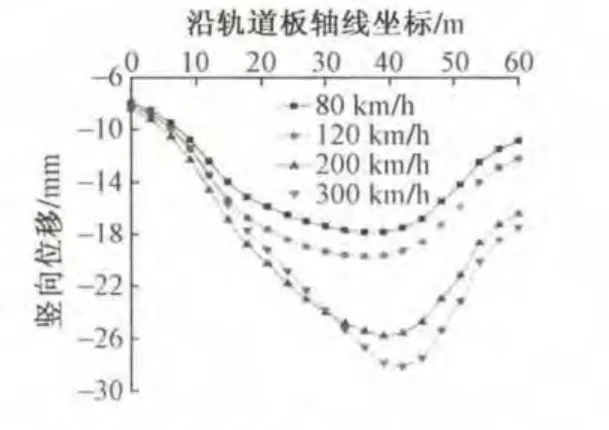
图3 地表最大位移曲线
3.2 位移时程结果
模型地表中部的位移随时间的变化曲线如图4所示。由图4可以明显看出地表最大瞬时沉降值随列车通过速度的增加而增大;位移衰减程度随着列车通过速度的增大而减小。
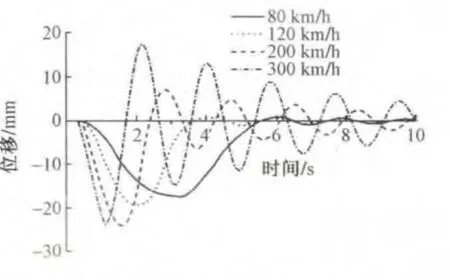
图4 地表沉降时程结果曲线
4 结论
1)高铁列车通过时列车荷载对地表沉降影响较大并且受列车通过速度影响很大。当以300 km/h的速度通过时地表产生的沉降最大达到28.8 mm,并且会造成地表较大范围内土体隆起。
2)根据地表的沉降时程曲线,受列车荷载波动影响最大沉降发生在列车完全通过后一定时间内。通过速度越大,地表位移衰减速度越慢,振动范围越大,振动周期越短。
3)根据数值模拟结果,列车通过下穿段的速度改变对地表沉降和地铁隧道结构影响较大,当车速>200 km/h时,地表沉降>20 mm,将会影响行车安全,并且对隧道结构的影响也相对较大。因此,当地铁隧道处于施工状态时,建议高铁列车通过速度≤120 km/h;地铁隧道竣工投入运营后,建议高铁列车通过此段时将车速控制在200 km/h内。
4)虽然路基沉降满足既定要求,但是根据以往工程经验,沉降量仍然偏大。可以通过改变注浆体参数或者采用其他注浆方式以提高注浆体强度,控制路基沉降量在更小的范围内。
[1]徐干成,李成学,王后裕,等.地铁盾构隧道下穿京津城际高速铁路影响分析[J].岩土力学,2009,30(增 2):269-276.
[2]霍军帅,王炳龙,周顺华.地铁盾构隧道下穿城际铁路地基加固方案安全性分析[J].中国铁道科学,2011,32(5):71-77.
[3]许恺,练松良,黄俊飞.地铁施工穿越铁路车站对列车限速的影响[J].同济大学学报,2003,31(2):174-177.
[4]张学钢,黄阿岗,郭旺军.列车荷载长期作用下隧道地基固结变形的数值分析[J].铁道工程学报,2011(4):22-26.
[5]张玉娥,白宝鸿.高速铁路隧道列车振动响应数值分析方法[J].振动与冲击,2001,20(3):91-93.
[6]罗建华.客运专线线下工程工后零沉降建设理念探索[J].路基工程,2008(3):73-74.
[7]FREYSTEIN H.MUNCKE M.德国铁路基础设施设计手册[M].2007.
[8]中华人民共和国铁道部.TB/T 10621—2009 高速铁路设计规范(试行)[S].北京:中国铁道出版社,2009.
[9]王科甫.盾构隧道下穿客运专线沉降预测及控制研究[D].成都:西南交通大学,2011.
[10]邱延峻,张晓靖,魏永幸.列车速度对无碴轨道路基动力特性的影响[J].交通运输工程学报,2007,7(2):1-5.
[11]刘晶波,谷音,杜义欣.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075.
[12]李庆.盾构法施工及列车荷载作用下粉土地基沉降特性研究[D].郑州:河南工业大学,2011.

