一种新插值法在卫星导航广播星历中的应用
申俊飞,郑 冲,陈金春
(北京卫星导航中心,北京 100094)
1 引言
在卫星导航定位中需要不断地计算出导航卫星的瞬时坐标和速度,而卫星坐标和速度是根据接收到的广播星历来计算的,而每次计算都需要占用大量内存,影响计算速度。卫星在轨道上的位置和速度用星历表示,具体形式可以是卫星位置和速度的时间列表,也可以是一组以时间为引数的轨道参数。卫星通过发布星历参数为用户提供实时定位、精确导航以及授时等服务;用户根据提供的星历参数由用户终端设备按固定公式计算出的卫星位置和速度称之为导航卫星广播星历。当然,广播星历还包括其他一些如卫星钟等参数,这里只讨论星历中发播的轨道参数[1]。
广播星历是通过卫星导航系统的测轨分系统外推轨道得到,随着时间的推移,预报轨道会偏离实际轨道,导航和定位的精度降低,所以只能保证一定时间段内的精度要求。随着卫星导航系统的不断发展,一方面对广播星历的精度和实时性提出了更高的要求,因此,如何快速、精确、方便地为用户提供导航卫星的位置和速度信息是卫星导航定位应用中的一个极其重要的问题[2]。
2 新插值方法
考虑到提供给用户的广播星历的精确性和实时性要求,广播星历应是尽可能精确的提供卫星轨道预报值,即考虑了卫星所受的地心引力和各种摄动力;广播星历参数能很好的拟合这些值,计算误差应尽量小,用户利用广播星历参数计算卫星位置的过程应尽量简单。
为此,将导航卫星星历表示为某种特定的多项式(即将一定时间段内的卫星星历拟合于选定的多项式),然后将多项式系数作为星历参数广播给用户是一种可行的方式。目前在星历数据处理中,应用较多的是Lagrange多项式插值,切比雪夫多项式在轨道拟合标准化中也由于其良好的插值精度有着广泛的应用[3-5]。
文献[6]提出了广义延拓插值法的基本原理与方法,并对其精度进行评价,但没有探讨三个参数的取值对插值结果的影响。本文采用广义延拓插值法进行导航卫星广播星历的插值,探讨了三个参数的取值与插值精度之间的关系。
3 广义延拓插值原理
广义延拓插值是在插值法和拟合法的基础上,发展起来的一种插值方法。它一方面在分片边界点上满足插值条件,使得分片之间的变化具有一定的协调性;另一方面又利用分片插值区域的周围节点的信息,实现分片区域内部的最佳拟合。
设函数u有一组离散数据
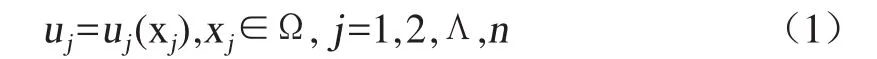
欲在区域Ω上构造一个近似函数U满足

将Ω划分为m个互不重叠的子区域Ωe(e=1,2,…,m),称作单元域Ω,单元域共有r个节点,其相应的节点坐标为xi(i=1,2,Λ,r),节点函数值为ui(i=1,2,Λ,r)。将单元域拓展,得单元延拓域Ωe'。
设Ωe'内有s个节点,其中属于Ωe的有r个节点(r 式中,g1(x),g2(x),Λ,gt(x)为Ωe'上的一组基函数;ak(k=1,2,Λ,t)为待定系数;t为逼近函数项数,且r 利用最佳平方逼近,求a1,a2,Λ,at,使 同时,使Ue(x)满足Ωe上的插值条件 将两式合并写成 由式(6)解出逼近函数式(3)中的待定系数,便可确定Ωe上的插值函数。式(6)称为广义延拓逼近方法的数学模型。 本文中用美国国家大地测量机构(National Geodetic Survey,NGS)提供的精密星历来进行广义延拓插值计算,然后对结果进行分析。轨道拟合的效果受到多项式阶数、拟合时段长度等参数的影响,分析这些参数的影响以及参数间的关系对于更好地使用广播星历有一定的意义。 目前,NGS精密星历采样间隔为15min,本文采用NGS跟踪站提供的2002年1月1日PRN1卫星15min等间隔的GPS精密星历,利用广义延拓插值法将15min间隔的数据插值到5min间隔,依次改变单元域节点数r、延拓域节点数s和逼近函数的项数t等三个参数的取值,组成多种组合,比较在取不同参数时插值的精度,分析参数和精度之间的关系,并与GPS精密坐标的值进行比较,计算结果见表1。 表1中给出了三个参数取得不同值时,广义延拓插值结果与精密星历坐标的最大差值。可以看出,三个参数的取值和插值精度之间存在着一定的规律,当三个参数取值较小时,插值误差较大,r=3,s=5,t=4时最大误差可达到90米以上。随着r,s,t三个参数的增大,插值的精度不断提高,在一定的范围内,精度保持稳定,具有较高的精度。从表1中数据可以看出,插值精度与参数s的关系最为密切,可以看到当s大于10时才能得到较高的插值精度;而当s的取值固定时,插值精度随着t的变化而改变,t和s越接近,插值精度就越高,当t=s-1时,精度最高。一般地,当s大于10后,再增加三个参数的值,插值精度基本保持稳定,不会有明显的变化,可以认为r=7,s=11,t=10即满足需要。X,Y,Z的最大误差为2.7mm,2.1mm,1.8mm,具有很高的精度,达到毫米级。参数继续增加时,计算量增加,插值精度反而不断降低。 表1 插值结果与GPS精密坐标比较 由以上可见,用广义延拓插值法是可以满足导航定位精度要求的。对于广播星历来说,如果采用r,s,t三个参数分别为7,11,10时,在广播星历播送时,只需要知道X,Y,Z三个方向上的系数ak(k=1,2,Λ,t),即t=10时共计30个参数即可。 并且这30个参数可由主控站将卫星在在地球协议坐标系中的轨道直接拟合得到。用户收到这30个广播星历参数后,应用广义延拓逼近多项式,可直接计算卫星在地球协议坐标系中对应时刻的位置和速度,无需进行坐标转换,物理意义明确,计算简单,速度快。 由以上结果分析,可以得到以下结论: (1)用项数为10的广义延拓逼近多项式逼近拟合卫星轨道,将多项式系数作为导航卫星星历参数广播,这是一种新的广播星历形式。导航定位终端利用这组星历参数解算实时导航定位时所需卫星轨道,方法简单、快捷。 (2)利用这组星历参数解算卫星轨道,其优点是计算过程简洁,计算速度快,占用计算机内存空间少,能满足精度要求等;同时,对广义延拓逼近多项式系数可根据实际精度需要进行合理选择。该方法在GPS定位测量中,为实现卫星轨道标准化提供了一种较好的、行之有效的方法。 (3)这种方法是否适用于具有多种轨道类型的导航卫星系统还待研究,这对于我国具有多种轨道类型共存的北斗二号卫星导航系统具有一定的参考价值。■ [1] 朱俊,文援兰,廖瑛.一类适用于各种轨道类型的导航卫星广播星历研究[J] .航天控制,2005(12) [2] 陈春花,高成发.卫星轨道标准化及其算法实现[J].现代测绘,2008(5.) [3] 丁文武,刘万科,李征航.基于广播星历的GPS卫星坐标的多项式拟合算法[J].海洋测绘,2007(10) [4] 陈正阳,易重海.用切比雪夫多项式进行GPS卫星轨道标准化[J].矿山测量,2002(6) [5] 李明峰,江国焰,张凯.IGS精密星历内插与拟合法精度的比较[J].大地测量与地球动力学,2008(4) [6] 施浒立,颜毅华,徐国华.工程科学中的广义延拓逼近法[M].北京:科学出版社,2005
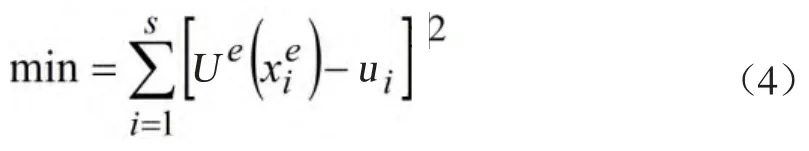
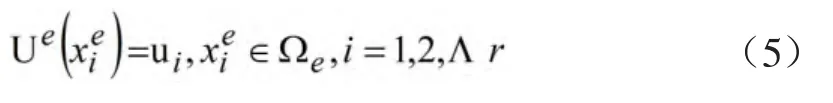
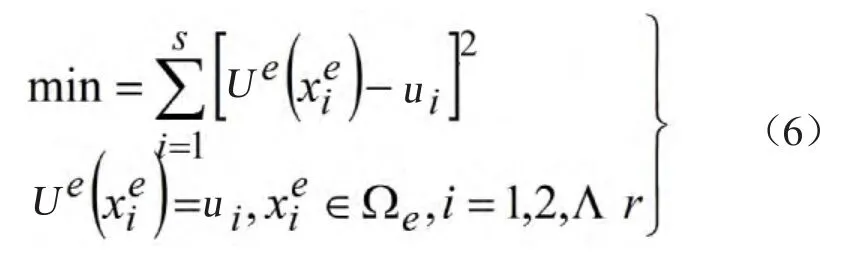
4 结果分析及应用
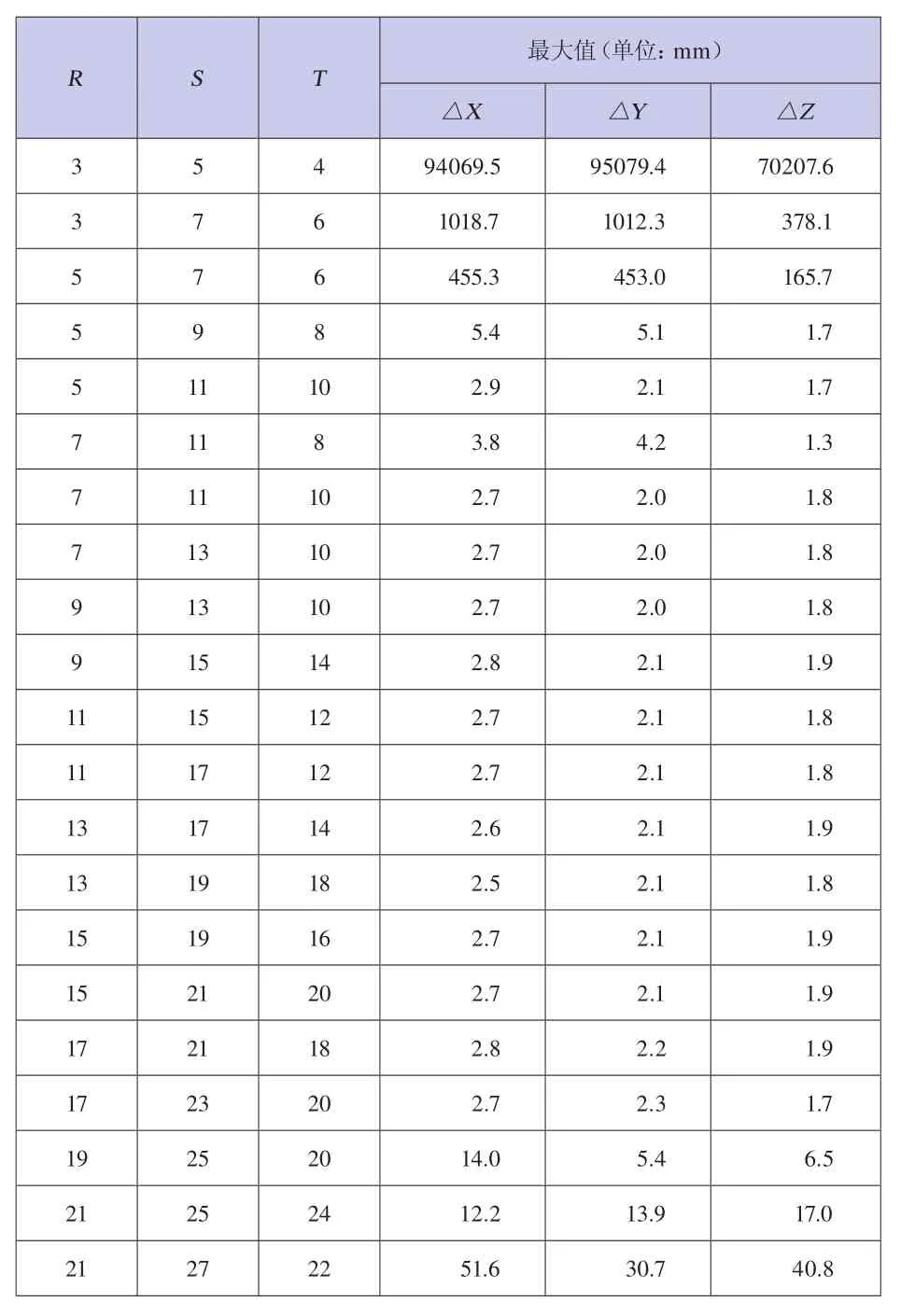
5 结束语

