高动态GPS接收机捕获技术研究
王 璇,郇 浩,赵玉梅,陶 然,贾丽娟
(北京理工大学信息与电子学院,北京 100081)
1 引言
GPS接收机接收到卫星信号后,必须先对信号进行捕获,才能开始信号的跟踪、伪距测量、定位导航等后续处理流程,因此,信号捕获是接收机的最关键技术问题之一。传统的信号捕获方法有基于时域自相关的串行搜索技术、基于快速傅里叶变换(FFT)的循环相关捕获技术和基于FFT的分段匹配滤波快速捕获技术。但是,在高动态条件下,由于载体高速及高加速运动使信号产生了较大的多普勒频率,并伴随有较大的多普勒频率变化率,这使得信号的捕获变得非常困难。传统基于FFT的快速捕获方法只能补偿接收机高速运动引起的多普勒频率分量,难以对由加速度引起的多普勒频率变化率分量进行有效补偿。本文在对传统信号捕获方法进行分析的基础上,提出了基于分数阶傅里叶变换(FRFT)的捕获方法,在对多普勒频率进行补偿的同时对多普勒频率变化率分量进行有效补偿,解决了传统方法在高动态环境下难以对信号进行长时间相干积累的难题。同时,为了进一步提高检测信噪比,本文通过对相干积累和非相干积累所获得的信噪比增益的详细分析,并根据GPS信号的特点,提出一种高效的积累策略。理论分析和仿真结果表明,本文所提出的方法能提高信号的捕获概率,缩短捕获时间,在高动态环境下易于实现信号的快速捕获。
2 GPS信号捕获方法
2.1 基于时域自相关的串行搜索技术
基于时域自相关的串行搜索技术一般用于GPS硬件接收机中。接收机在搜索到卫星的伪随机噪声(PRN)码后,针对此PRN码对载波频率和伪码相位进行二维搜索。此种方法实现简单,但是捕获时间长,一般情况下不采用。
2.2 基于FFT的循环相关捕获技术
基于FFT的循环相关捕获技术是利用本地PRN码与输入信号做相关,在搜索一个载波频点的同时,完成整个PRN码相位的搜索。此方法将时域内的相关运算转换成频域内的相乘,当本地PRN码与接收信号中的PRN码对齐时,就会输出对应的相关峰值,这样就将载波频率、伪码相位二维搜索降为一维频率搜索,大大缩短了捕获时间。但是此方法在进行傅里叶变换及其逆变换时,会有大量的复乘运算,运算复杂度较高,一般也不采用。此方法的捕获原理如图1所示。
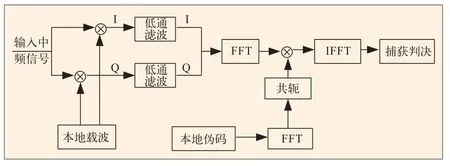
图1 基于FFT的循环相关捕获技术原理框图
2.3 基于FFT的分段匹配滤波快速捕获技术
基于FFT的分段匹配滤波快速捕获技术,在搜索一个伪码相位的同时完成整个多普勒频率范围的搜索,同样是将二维搜索降为一维搜索,缩短了捕获时间。其基本思想是:将输入信号与本地PRN码相乘进行伪码剥离,本地PRN码相位与输入信号对齐时会得到一个连续的正弦波,这样对信号进行FFT谱分析就可以很容易得到载波多普勒频率的估计值。这种方法减少了做FFT的点数,使运算量大大降低,加快了整体的捕获速度。此方法的捕获原理框图如图2所示。
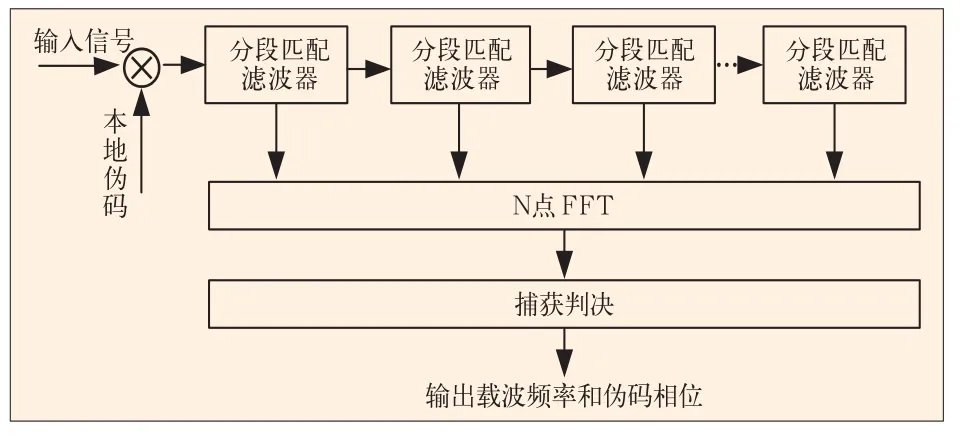
图2 基于分段匹配滤波器捕获技术原理框图
2.4 传统捕获方法性能分析
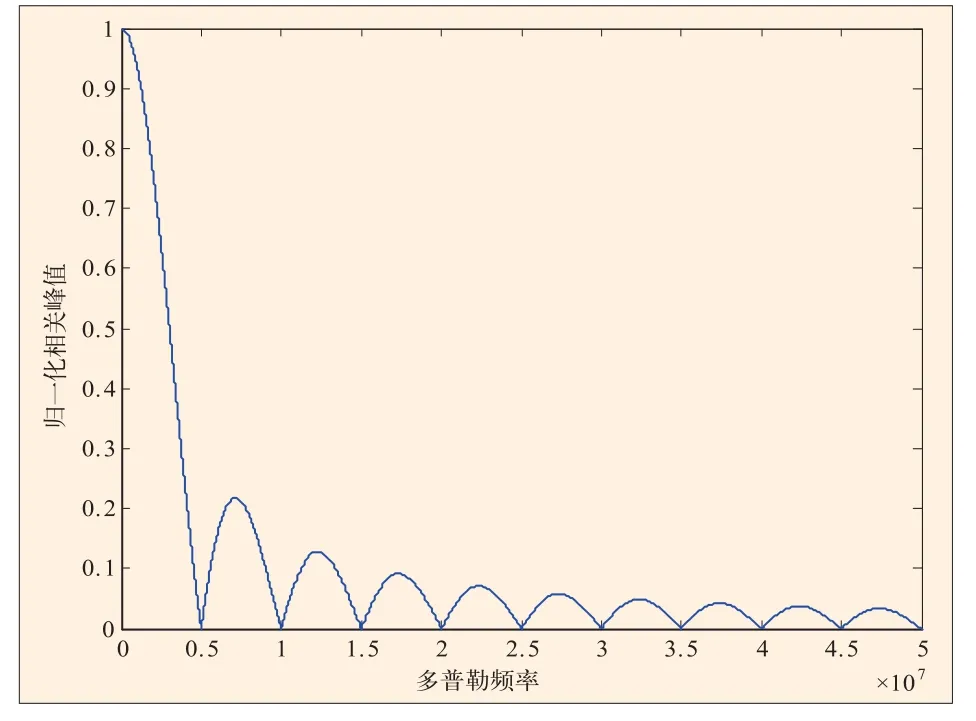
图3 多普勒频率对相关峰的影响
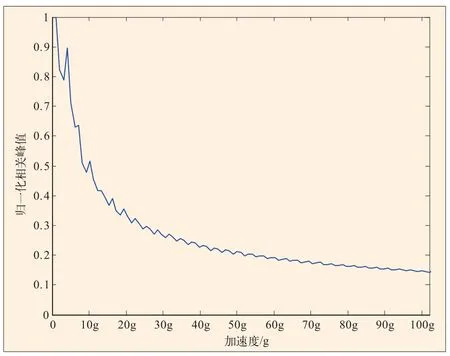
图4 加速度对相关峰的影响
现对高动态环境下传统方法的捕获性能进行分析。在高动态环境下,接收机必须满足实时性的要求,即能对高动态信号进行快速捕获。其中PRN码和载波多普勒的捕获速度是影响接收机捕获速度的两个重要因素。基于时域自相关的串行搜索技术需要对伪码相位和载波多普勒频率进行二维搜索,显然不能满足高动态接收机实时性的要求。基于FFT的捕获方法虽然将传统的二维搜索降为一维搜索,加快了信号的捕获速度,但是在高动态环境下,由于载体的高速及高加速运动,使调制载波信号产生较大的多普勒频率和多普勒频率变化率,这会对信号做FFT之后的相关峰产生很大的影响。图3是相关峰值和多普勒频率之间的关系仿真曲线,可以看出,多普勒频率越大,相关峰值越小。图4是加速度与相关峰值之间的关系曲线,仿真结果表明,随着加速度的增大,相关峰值是减小的。因此在高动态环境下,基于FFT方法的捕获效果并不理想。
3 分数阶傅里叶域的相干积累和非相干积累
3.1 基于分数阶傅里叶变换的快速捕获技术
以上分析表明,传统的捕获方法不适合高动态信号的快速捕获。高动态环境下,调制载波信号呈现出近似线性调频(chirp)信号的形式。传统基于FFT的捕获方法只能补偿接收机高速运动引起的多普勒频率分量,而不能对由高加速运动引起的多普勒变化率分量进行有效补偿。针对以上问题,本文提出了基于分数阶傅里叶变换的高动态信号捕获方法,能同时对载波多普勒频率及其变化率分量进行有效补偿。
分数阶傅里叶变换是一种新兴的时频分析工具,它利用线性调频函数(chirp基)对信号进行分解,因此它特别适合处理chirp类信号。本方法利用分数阶傅里叶变换对线性调频(chirp)信号的聚焦特性对信号进行捕获。
分数阶傅里叶变换的定义为:
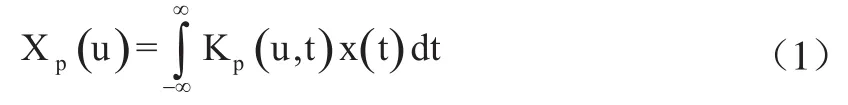
式中,p=2α/π,为分数阶傅里叶变换的阶次;α为旋转角度;Kp(u,t)为分数阶傅里叶变换的核函数,其定义为:
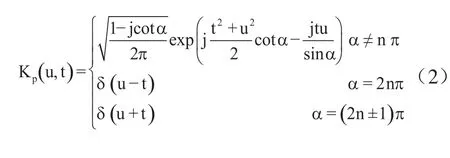
在此我们用离散分数阶傅里叶变换(DFRFT),其定义为:

式中,Δu=(2N+1)·|cosα|·Δt/2M+1,Δu和Δt分别是Xp(u)和x(t)的采样间隔。利用上式定义的离散分数阶傅里叶算法只需两次chirp乘积和一次FFT运算,运算量小,运算速度快,能够快速实现信号最优阶次的分数阶傅里叶变换。当本地PRN码与输入信号对齐时,会在相应的分数阶傅里叶域输出相关峰值,进而得到伪码相位、载波多普勒频率及其变化率的估计值。在实现时可以根据载体加速度的搜索范围对输入信号做最优阶次的分数阶傅里叶变换。当变换阶次p=-(2/π)arccot(2fca/c)时,实现了分数阶傅里叶域的相干积累,其中fc为射频载波频率,α为载体的加速度,c为光速。仿真结果表明在信噪比较低、载体加速度较大的情况下,传统基于FFT的方法不易捕获到信号,而基于分数阶傅里叶变换的方法能很好的捕获到信号。图5和图6分别是基于FFT和基于FRFT的高加速、低信噪比信号捕获仿真图。从仿真图可以看出,当载体存在高加速运动时,传统的基于FFT的方法所获得的相关峰并不是特别明显,而基于FRFT的方法却能得到较明显的相关峰,易于实现信号的捕获。
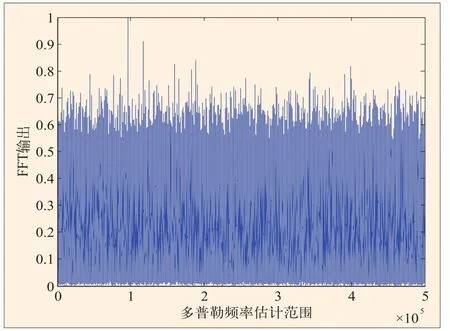
图5 基于FFT的高加速、低信噪比信号捕获
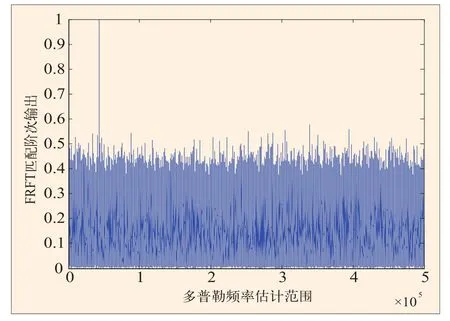
图6 基于FRFT的高加速、低信噪比信号捕获
3.2 相干积累和非相干积累
载体的高动态运动导致接收信号的强度会发生剧烈变化,信号的信噪比也相应产生剧烈变化,因此接收机接收到的GPS信号一般情况下信噪比极低,这就要求GPS接收机具有一定的抗噪声性能,能在低信噪比的情况下提取卫星信号。由于GPS信号是直接序列扩频信号,其抗噪声性能与扩频增益成正比,若我们选取一个数据码周期的信号进行处理,可以获得较高的扩频增益,但是由于数据比特跳变的影响,信号的选取不能太长,一般选取一个伪码周期长度的信号进行处理,这样只能获得低的扩频增益,降低了捕获过程的抗噪声性能。为了降低噪声的影响,获得高的检测信噪比,常用的方法是对信号进行相干积累和非相干积累。当GPS信号中的伪码被剥离掉后,输入信号变为连续的正弦波,对其进行谱分析便可得到载波频率,这一过程称为相干积累。相干积累是GPS信号捕获中的第一步。对多个相干积累的输出幅值进行相加称为非相干积累。但是进行相干积累和非相干积累时间长度的选取需要折中考虑,且两种方法所获得的信噪比增益是不同的。现对其进行建模分析并仿真验证。
选取两个伪码周期,即2ms长的信号进行分析,则进行伪码剥离后的数字基带信号为x(n)=ejwn+ε(n)(此处忽略数据跳变的影响,省略了调制在信号上的数据码信息),假设总共有2N个点,信号上混有高斯白噪声ε(n)。将信号平均分成两段x1(n),x2(n),每段长1ms,考虑对信号做以下几种处理后的检测信噪比:
(1)对连续2ms信号x(n)进行相干积累,即
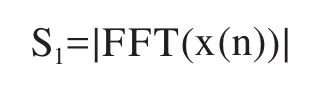
(2)对x1(n),x2(n)进行1ms分段相干积累,即
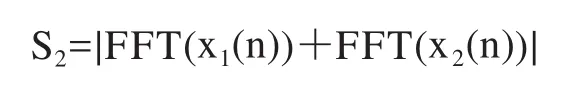
(3)对x1(n),x2(n)进行1ms分段非相干积累,即
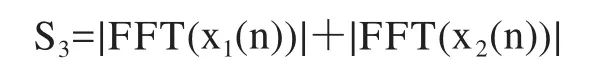
首先从定义的角度对1和2两种方法进行分析:
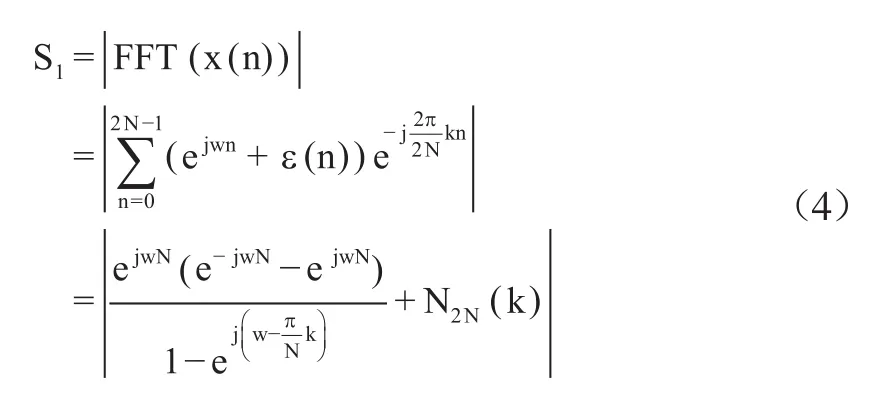
式中,N2N(k)表示对噪声做2N点的FFT。
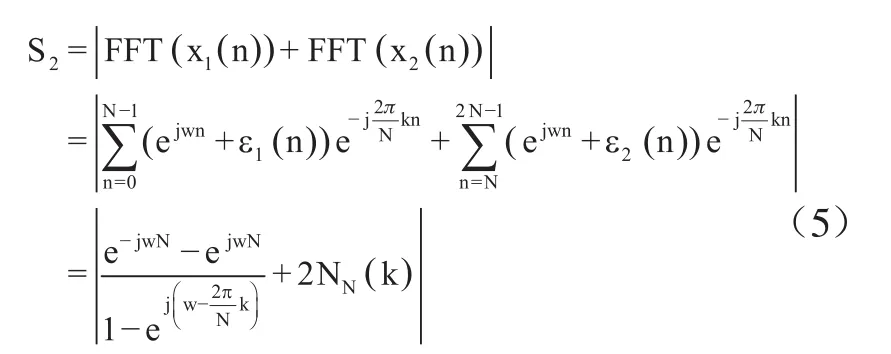
式中,N2N(k)表示高斯白噪声的2N点FFT;NN(k)表示噪声的N点FFT,N2N(k)=2NN(k)。观察(4)式和(5)式可知,两种情况其结果差别主要体现在相位上。由于多普勒频率的不确定性,被截断的信号可能为非整周期,这导致FFT后的信号在相加时,受信号截断相位的影响,幅度互相抵消,信号幅值降低。而当被截断的信号为整周期时,两种情况所得的幅值是相等的。
为了更直观的说明这两种情况的效果,在多普勒频率分别为5000Hz,5300Hz,5500Hz时,分别取2ms载波信号按上述两种方式进行处理。图7是多普勒频率为5000Hz时的情况,图中正弦信号在截断前和截断后都是整周期的,此时2ms相干积累和1ms分段相干积累所得信号峰值相等。图8是多普勒频率为5300Hz的情况,此时2ms信号并非整周期,被截断的两段1ms信号也是非整周期的,且两段信号的起始相位是不同的,这样分段相干积累后,信号幅值较2ms相关积累更低,大约下降2.77dB。图9是多普勒频率为5500Hz的情况,2ms信号包含11个载波周期,但是被截断为两个1ms长的信号后,两段信号的起始相位正好反向,这导致分段相干积累后的幅值大大削减,结果几乎为0。为了补偿这种相位差引起的峰值削减问题,一般可以首先计算截断的两段信号的相位差,当相位差的绝对值小于π/2时,
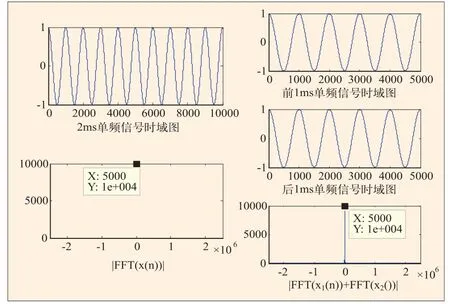
图7 fd=5000Hz时,2ms相干积累和2ms分段相干积累
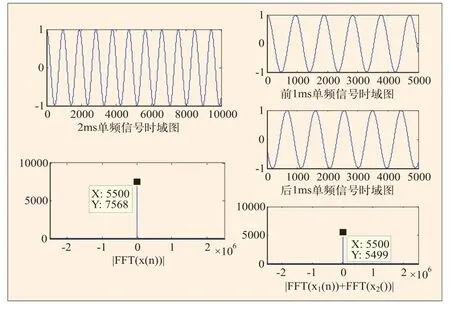
图8 fd=5300Hz时,2ms相干积累和2ms分段相干积累
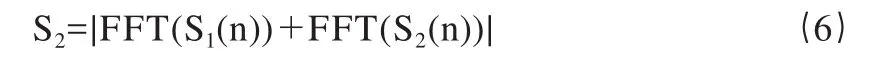
当相位差的绝对值大于π/2时,
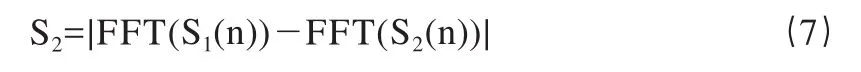
对S2和S3两种方法进行分析:
S2为分段相干积累,两段信号分别做FFT后对其和取模值,相当于信号的幅值变为原来的二倍,信号的功率变为原来的四倍。而信号中叠加的噪声是高斯白噪声,可正可负的白噪声进行相加,其分布特性不变,噪声的功率变为原来的二倍。因此采用相干积累方法后,信噪比变为原来的二倍。相对于1ms数据进行相干积累的信噪比,对n ms数据进行相干积累后,其信噪比增益G为:

因此相对于1ms的相干积累,S2的信噪比增益为3dB。
S3为非相干积累方式,两段信号分别做FFT且取模后再求和,信号的幅值变为原来的二倍,功率变为原来的四倍,但对信号进行求模运算的同时也对噪声进行了求模运算,其分布特性不再是高斯分布,均值不为零,噪声功率比大于原来的二倍,这就引入了平方损耗。
假如同相和正交两路信号1ms相干积累的结果为I和Q,其中叠加的噪声分别为nI和nQ,它们都是均值为0,方差相等的高斯白噪声,则求模运算后信号的功率为:
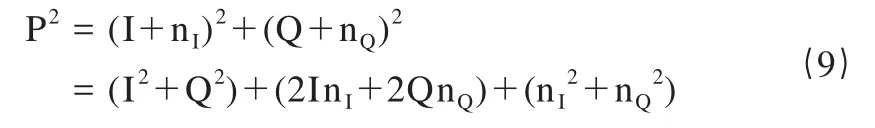
从(9)式可以看出,最后一项噪声不再服从高斯分布,均值也不为0,这是平方损耗的根源所在。非相干积分的平方损耗定义为:
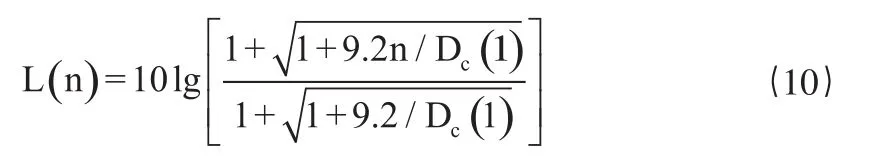
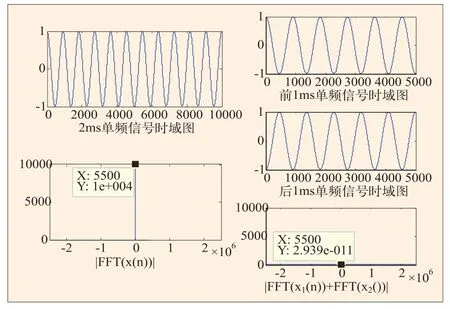
图9 fd=5500Hz时,2ms相干积累和2ms分段相干积累
式中,n为相对于1ms的非相干积分个数;Dc(l)为理想检测能力因子,是检测概率Pd和虚警概率Pfa的函数,其定义为:
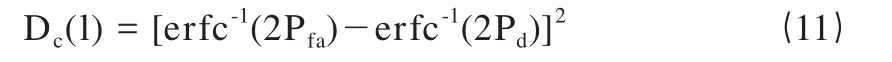
式中,erfc-1(y)为互补误差函数的反函数。则非相干积累的信噪比增益为:

因此相对于1ms的相干积累,S3的信噪比增益显然要小于3dB。
由以上分析可知,与相干积累方式相比,非相干积累对系统检测信噪比的改善要弱一些。因此为了提高捕获概率,增强系统的抗噪声性能,我们可以适当选取较长时间的信号进行相干积累,然后对多个相干积累的输出进一步做非相干积累,以获得高的信噪比增益。
在分数阶傅里叶域对信号进行相干积累与非相干积累,其原理与在傅里叶域是一样的。但是由于载体加速度的影响,相关峰值输出频率点的位置会发生偏移,因此在分数阶傅里叶域进行非相干积累时需要对相干积累输出结果进行相应的时间频率调整,以保证在相同频率点上的相关幅值得到增强,达到提高信噪比的目的。
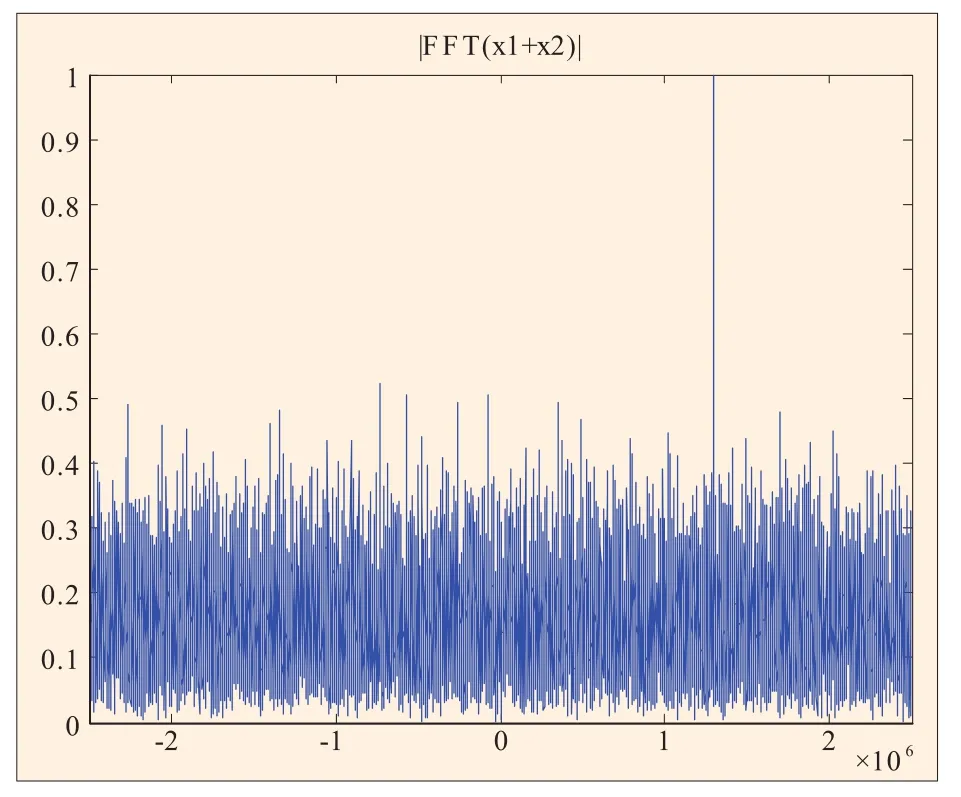
图10 连续2ms相干积累(fd=50kHz)
4 仿真验证
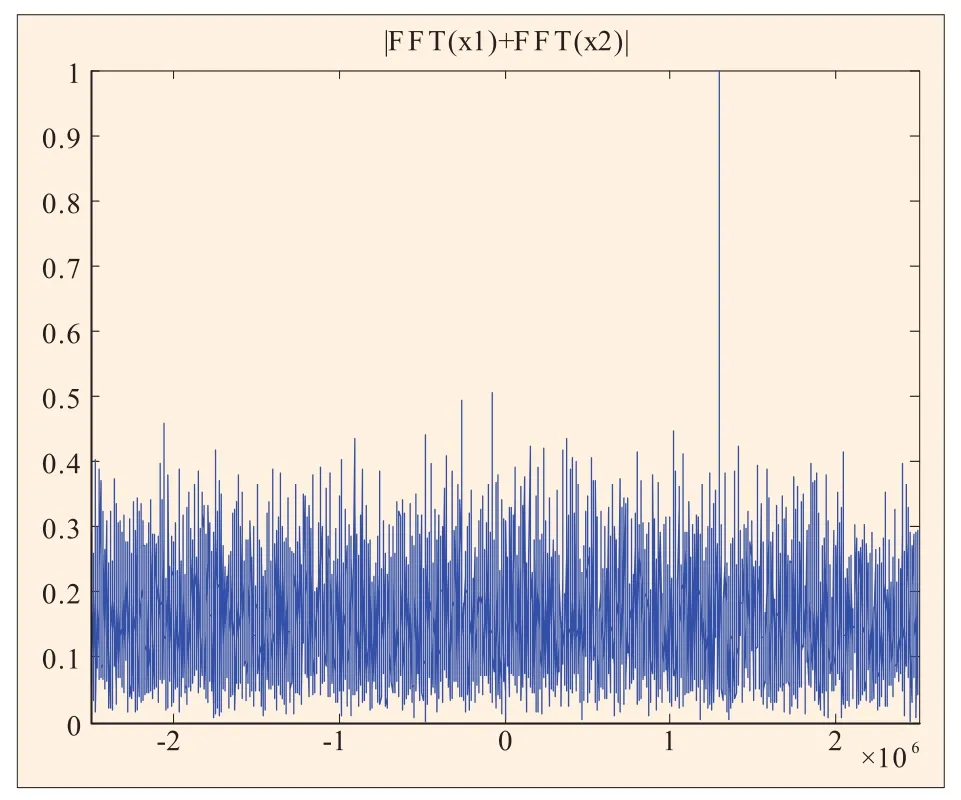
图11 1ms分段相干积累(fd=50kHz)
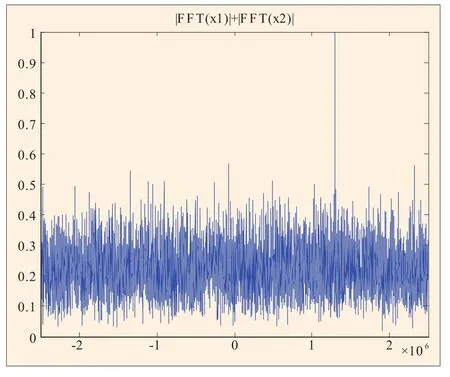
图12 1ms分段非相干积累(fd=50kHz)
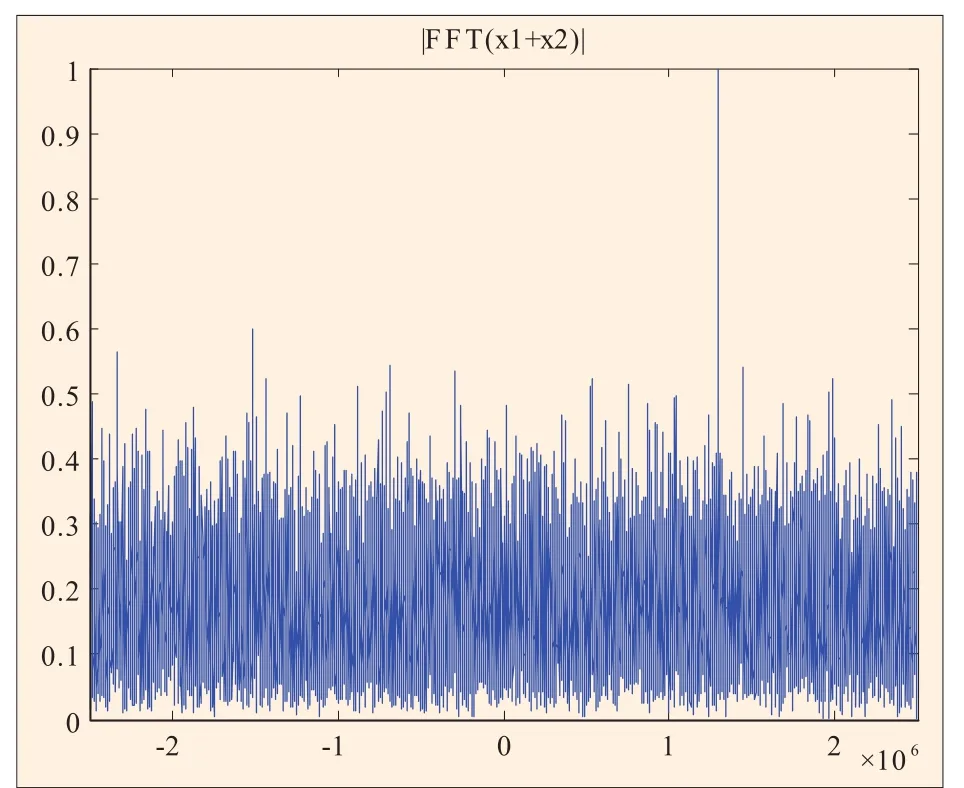
图13 连续2ms相干积累(fd=50.353kHz)
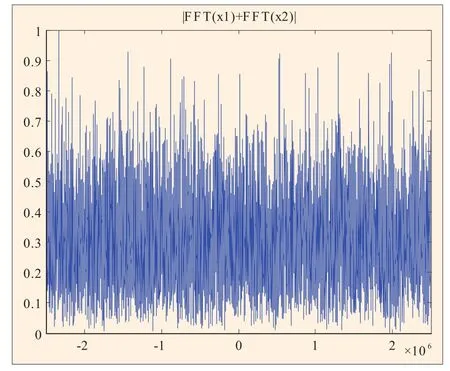
图14 1ms分段相干积累(fd=50.353kHz)
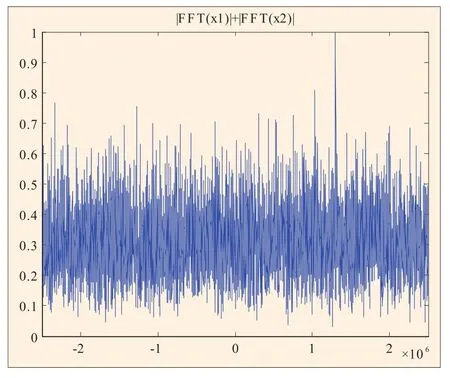
图15 1ms分段非相干积累(fd=50.353kHz)
仿真实验采用实测的GPS数据,正交下变频后中频频率为21.25MHz,假设多普勒频率分别为50kHz和50.353kHz,采样频率为5MHz,则在MATLAB中输出的数字频率分别为1.3MHz和1.300353MHz。选取2ms的数据进行仿真验证,假设本地PRN码与输入信号完全对齐,在不同多普勒频率的条件下,分别对信号进行连续2ms相干积累、1ms分段相干积累和1ms分段非相干积累,频率分辨率分别为500Hz和1kHz,其仿真结果分别如图10至图15所示,在不同输入信噪比情况下,所得的检测信噪比如表1和表2所示。
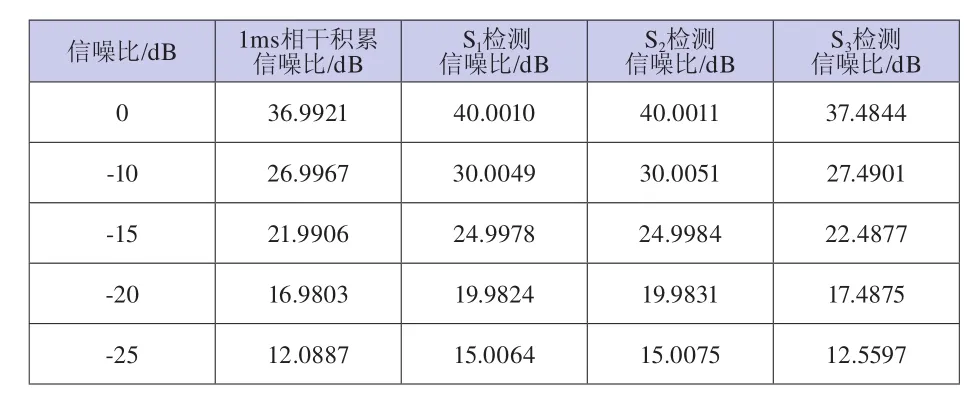
表1 检测信噪比(fd=50kHz)
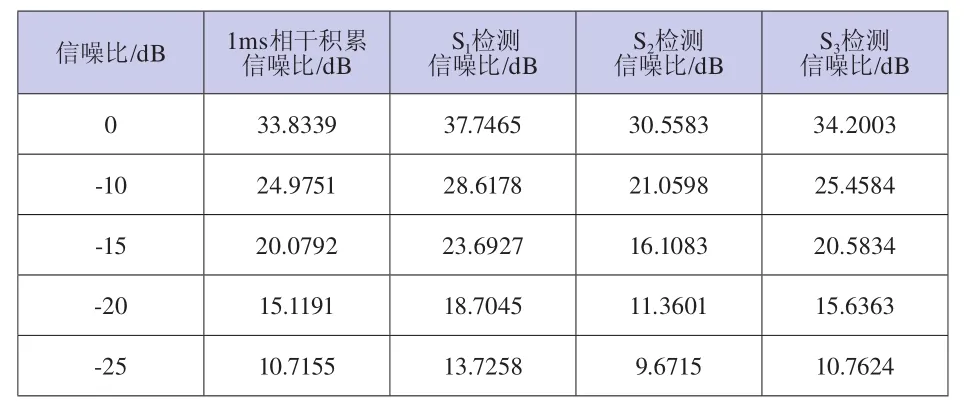
表2 检测信噪比(fd=50.353kHz)
以上仿真图和仿真数据表明,当输出频率使信号截断后仍为整周期时,信号连续2ms相干积累所得的检测信噪比与1ms分段相干积累所得的检测信噪比是相等的,并且相对于1ms相干积累的信噪比增益大约为3dB,而1ms分段非相干积累所得的信噪比增益较低。当输出频率使信号截断后为非整周期时,信号连续2ms相干积累所得的检测信噪比明显要高于1ms分段相干积累所得的检测信噪比,与理论分析相符。从仿真图也可以看出,图13中并没有出现明显的相关峰值,不易于信号的捕获。表2中的数据也表明此时1ms分段相干积累所得检测信噪比增益很低,甚至使信噪比恶化。因此,为了提高检测信噪比,增强系统的抗噪声性能,在不受数据比特跳变影响的情况下,我们可以适当选取较长时间的信号进行相干积累,然后对其输出进一步做非相干积累,以获得高的信噪比增益。
5 结束语
本文在对传统捕获方法进行分析的基础上,提出了一种新的基于分数阶傅里叶变换的捕获方法,在高动态、低信噪比情况下,能显著提高信号的检测信噪比,易于实现信号的捕获。为了进一步提高检测信噪比,一般需要采取相干积累和非相干积累的方法。本文对相干积累和非相干积累方法进行了详细的建模分析并仿真验证,指出受多普勒频率的影响,对长度相同的信号进行连续相干积累和分段相干积累所得信噪比是不同的,并提出在不受数据比特跳变影响的前提下,可适当选取较长时间信号进行相干积累以提高检测信噪比,然后对多个相干积累的输出做非相干积累,进一步提高检测信噪比。理论分析和仿真结果表明,本文提出的方法能显著提升输出信号的信噪比增益,增强系统的抗噪声性能,易于实现高动态环境下信号的快速捕获。■
[1] GPS原理与应用(第二版)[M].寇艳红译.北京:电子工业出版社,2007
[2] 鲁郁.GPS全球定位接收机——原理与软件实现[M] .北京:电子工业出版社,2009
[3] Sascha M.Spangenberg, Iain Scott et al.An FFT-Based Approach for Fast Acquisition in Spread Spectrum Communication Systems[J].Wireless Personal Communications, 2000, 13: 27-56
[4] 徐峰,邵定荣,李署坚.一种高动态直扩接收机快速码捕获方法[J] .北京航空航天大学学报,2007, 33(6): 672-676
[5] 陶然,邓兵,王越.分数阶傅里叶变换及其应用[M] .北京:清华大学出版社,2009
[6] 王云,陈培,杨颖,陈杰.GNSS接收接最优中频积累时间研究[J] .电子科技大学学报,2010, 39(1): 21-24
[7] JAMES BAL-YEN TSUI.GPS软件接收机基础(第2版)[M] .陈军,潘高峰等译,北京:电子工业出版社,2007
[8] 张斌,孔敏,吴从兵.基于窗函数下频谱泄露的研究[J] .信息化纵横,2009:10-12.
[9] 谢钢.GPS原理与接收机设计[M] .北京:电子工业出版社,2009

