基于LLC 直流变压器（LLC-DCT）效率优化的死区时间与励磁电感设计

任 仁 张方华 刘 硕

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

随着信息技术和半导体器件的发展，同时对能量管理提出了更高的要求，高效率和高功率密度已经成为推动通信电源技术发展的关键因素。分布式电源系统架构由于其高性能和高可靠性被广泛采用在通信和计算机电源中，而其中 AC-DC 后端的DC-DC 变换器和中转母线变换器作为架构中关键组件也对效率和功率密度提出了更高的要求。

由于LLC 谐振变换器电压增益特性和很小的开关损耗，使它同时获得了高效率和宽输入范围的能力，如图1 所示，成为一个十分有潜力的拓扑并被广泛应用在分布式架构组件中。LLC 变换器可以工作在两个状态，即直流变换器（LLC-D2D）和直流变压器（LLC-DCT）。LLC-D2D 最常被使用在AC-DC 后端的DC-DC 变换器中，其参数设计在文献[1-8]中已经提出了很详细的方法。LLC-DCT 相比LLC-D2D，不存在补偿环路通过调节频率来稳定输出电压，而是维持一个恒定的直流增益比，所以常被使用在中转母线变换器中。同时为了维持恒定直流增益比，尽可能让其增益曲线在一定开关频率范围内平坦而不受温度等环境因素影响，这使得LLC-DCT 的参数设计与LLC-D2D 的参数设计存在一定的差异，但是基本没有文献提到LLC-DCT 参数设计的方法。

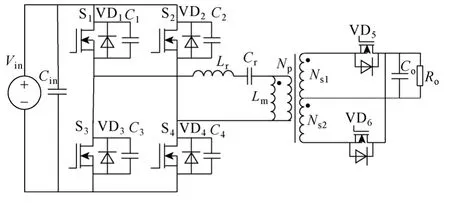
图1 LLC 谐振变换器拓扑Fig.1 Topology of the LLC converter

大部分涉及到LLC-D2D 参数设计的文献都参考了文献[1]，文献[1]通过推导原副边电流有效值得出了当LLC 工作在谐振频率时，影响导通损耗大小的唯一参数是励磁电感，励磁电感感值越大，其损耗越小。所以根据桥臂间换流的死区时间可以算出一个满足原边开关管ZVS 开通的最大励磁电感，认为该励磁电感值为最佳值。但该文没提到死区时间的选取，这导致励磁电感和死区时间存在无数组解，而其他文献中以PWM 变换器中的经验，认为保证桥臂不直通的情况下，死区时间越小，效率越高。本文在第2 节中仔细分析了原副边电流有效值、开关损耗和死区时间的关系，推出了定量表达式，最终从损耗和死区时间的曲线图上得到了效率最佳化的死区时间，从而确定了最佳励磁电感的感值。

最后针对低压大电流场合下LLC-DCT 工作特性，对励磁电感与谐振电感比值Ln的设计进行了讨论，并由此设计合适的Q值。

2 励磁电感和死区时间的最优化设计

2.1 原副边电流有效值与死区时间定量推导

无论是LLC-D2D 或者是LLC-DCT 均希望工作在谐振频率下，不仅可以获得最高的效率[9-11]，还可以获得不随负载发生变化的直流增益。图2和图3 分别为LLC 工作在谐振频率处的关键电流波形和等效电路，其中iLr为谐振电流，im为励磁电流。从图2 得出，谐振频率处的谐振电流为正弦波形，表达式为

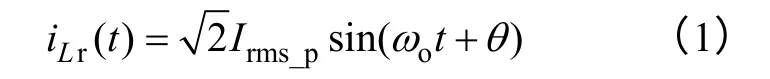
式中，Irms_p为原边电流的有效值；ωo为谐振频率的角频率；θ为谐振电流与励磁电感电流的相位差。

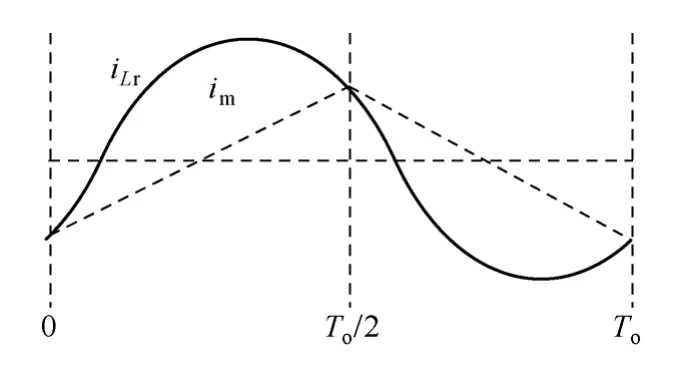
图2 谐振电流和励磁电感电流Fig.2 The resonant current and the magnetizing current

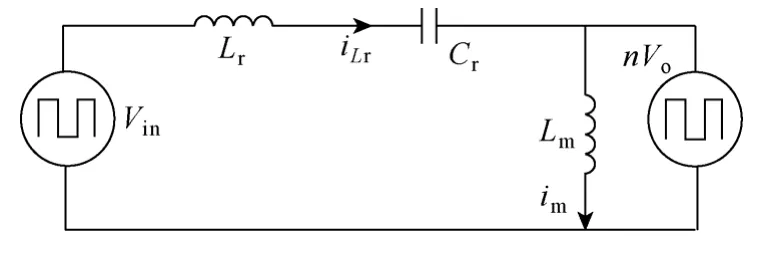
图3 谐振频率处的等效电路Fig.3 Equivalent circuit at resonant frequency

从图2 还可看出，二分之一谐振周期时励磁电流和谐振电流相等。此时为励磁电流的峰值，大小为

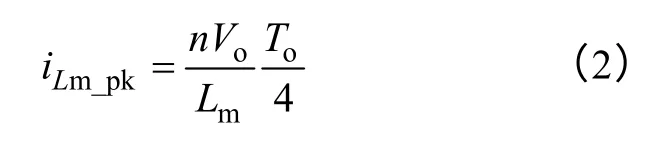
同时在二分之一谐振周期内，谐振电流与励磁电流之差的平均值为折算到原边的输出电流平均值。所以建立以下两个等式

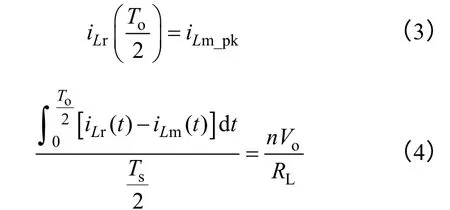
式中，RL为负载电阻；Ts为开关周期，To为谐振周期，和死区时间Td的关系为

由式（3）和式（4）可推出原边电流有效值的表达式为

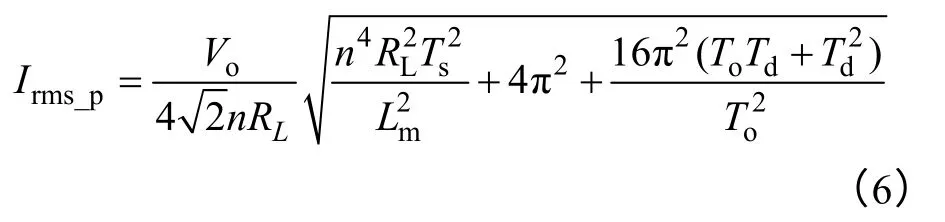
副边电流等效为原边谐振电流和励磁电流之差折合到副边的电流，所以副边电流有效值可以表达为

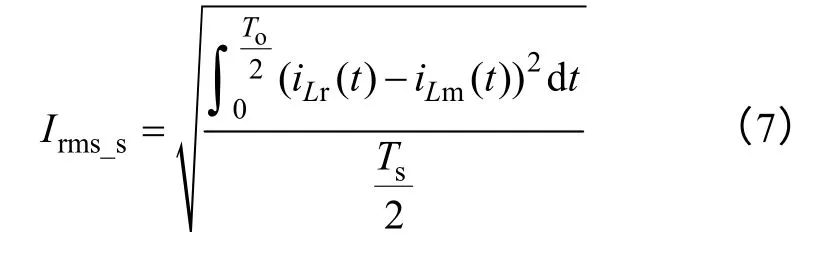
由式（1）和式（7）可以得出

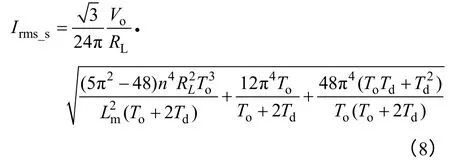
以上式子只在谐振频率处成立，为了不让Td变化对谐振周期造成影响，这里保证To不变，Td的变化只影响开关周期Ts。保证了以上式子在Td变化的情况下均成立。

同时为了实现原边开关管的ZVS 开通，应满足关断时励磁电流峰值足够来为开关管的结电容抽流。这里认为抽流期间，励磁电流为恒值，则应满足

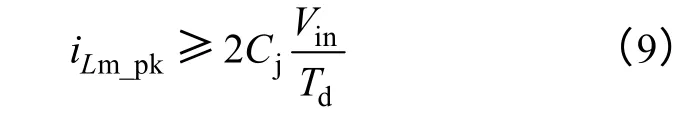
由式（2）和式（9）可以得到Lm和Td的一个约束关系为

式中，Cj为开关管结电容容值，为了取得最小的导通损耗，Lm在满足式（10）的条件下越大越好，所以可以由此建立等式

由式（11）可以看出，Lm和Td存在无数组解，不能凭借在PWM 变换器中的经验认为Td越小变换器效率越高而人为地将Td设定一个较小数值。无穷解里一定存在一组效率最优解，所以将式（11）分别代入式（6）和式（8）中，可以得到原副边电流有效值与死区时间Td定量表达式为

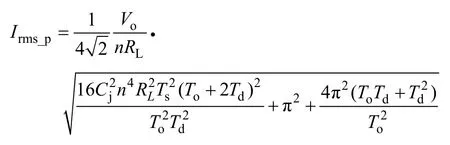
根据样机设计的谐振频率fo为500kHz，输入48V，输出12V，变压器电压比n=4，满载功率150W，原边开关管型号为infineon 公司的BSC047N08NS3，Cj在开关管DS 电压48V 下为1 000pF。将这些数据代入式（12）中，利用mathcad 可以画出原副边电流有效值和死区时间Td的曲线如图4和图5 所示。

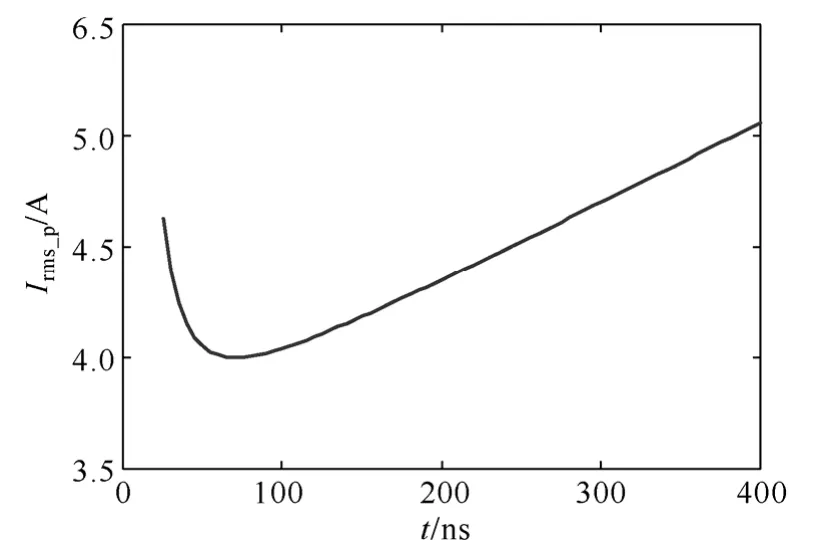
图4 原边电流有效值与死区时间曲线Fig.4 Relationship between the primary current and the dead time

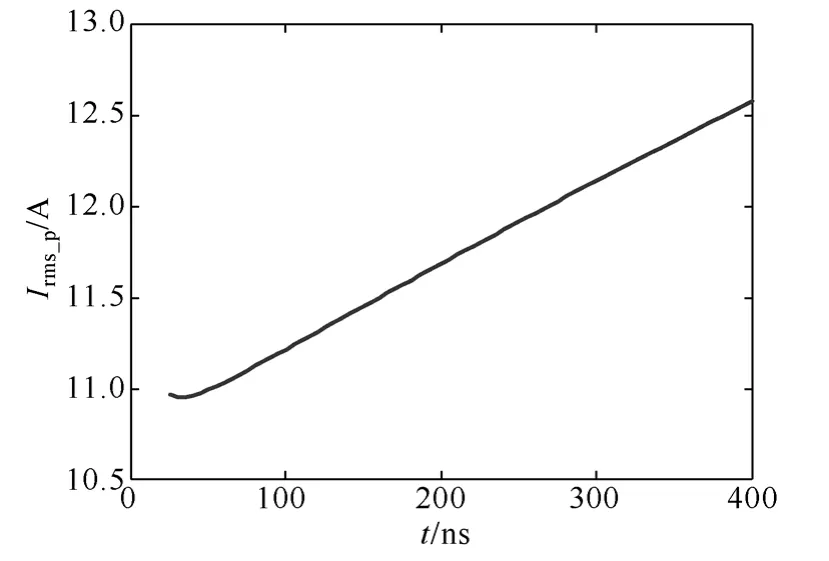
图5 副边电流有效值与死区时间曲线Fig.5 Relationship between the secondary current and the dead time

可以看出原边电流有效值和死区时间并不是单调关系，副边电流有效值基本与死区时间成正比，而导通损耗近似与原副边电流有效值成正比关系，所以导通损耗与死区时间也不是简单的单调关系，而是存在一个最小导通损耗对应的死区时间Td。

2.2 开关损耗与死区时间定量推导

LLC 的开关损耗集中在原边开关管的关断损耗上，与励磁电感电流的峰值有关。原边关断损耗可以粗略由式（13）表示。

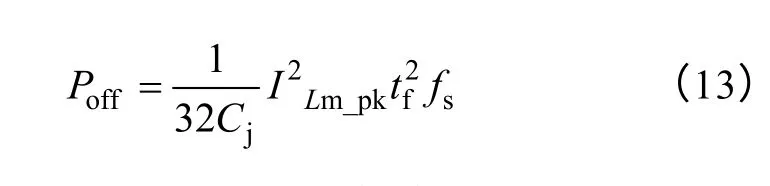
式中，ILm_pk为开关管关断时刻的电流，即为励磁电流峰值。tf为开关管关断电流下降时间。将式（2）、式（11）代入式（13）中，可以得到关断损耗与死区时间Td的定量表达式为

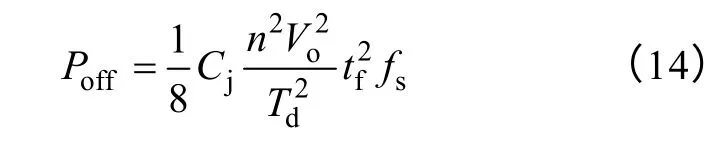
同样利用mathcad 可将开关损耗和死区时间Td的曲线图画出，如图6 所示。

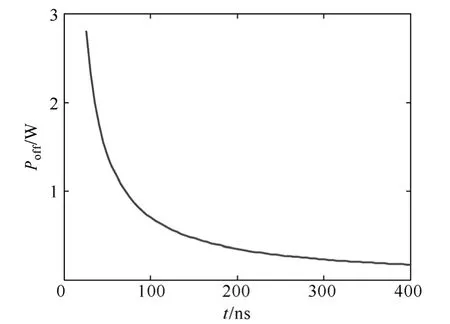
图6 开关损耗与死区时间曲线Fig.6 Relationship between the switching loss and the dead time

由图6 可以看出，开关损耗与死区时间成反比，死区越大，开关损耗越低。

2.3 总损耗与死区时间的关系

综合2.1和2.2 节分析，可以画出总损耗与死区时间的曲线图，如图7 所示。

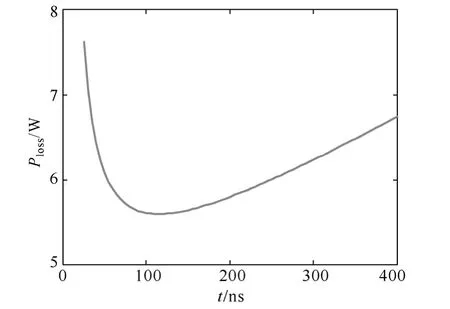
图7 总损耗与死区时间曲线Fig.7 Relationship between the total loss and the dead time

从图7 可以看出，并不是死区时间越小，损耗越小。而是存在一个最佳死区时间使得总损耗最小化，可以从图上读出来，该死区时间大小为125ns，根据式（11）的约束条件可以得到与之相对应的励磁电感值，即得到Lm和Td的最优化解为

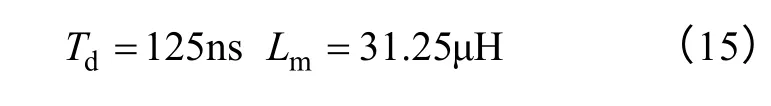
3 Ln与Q 值的优化选取

首先定义一下Ln和Q，Ln为励磁电感Lm和谐振电感Lr的比值，而Q为谐振腔的品质因数。Ln和Q的定义表达式为

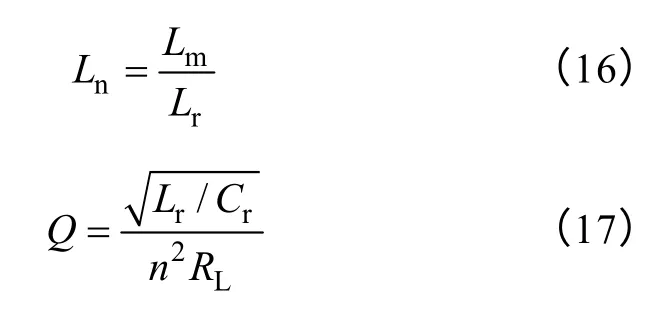
在谐振频率确定的情况下，可以看出Ln和Q是两个相关量，只要其中一个确定就可以确定另外一个。LLC-D2D 设计中，因为要获得宽输入范围，所以要对其最大增益有一定要求。如图8 所示的是一组固定Q值，不同Ln值下LLC 增益曲线。可以看出Ln越小，增益峰值越高，而且对于需要闭环调频来稳压的LLC-D2D 而言，较小的Ln可以实现较窄的变频范围。但是对于LLC-DCT 来说，希望在较宽的频率范围内都保持较为一致的增益，这样不仅可以抑制温度环境等因素对谐振参数的影响，还可以在不同负载下获得稳定的直流增益。所以 LLCDCT 一般会选取较大的Ln值，同时较大的Ln使得Lr的感值减小，便于磁集成在变压器中或者使用变压器漏感来充当谐振电感。

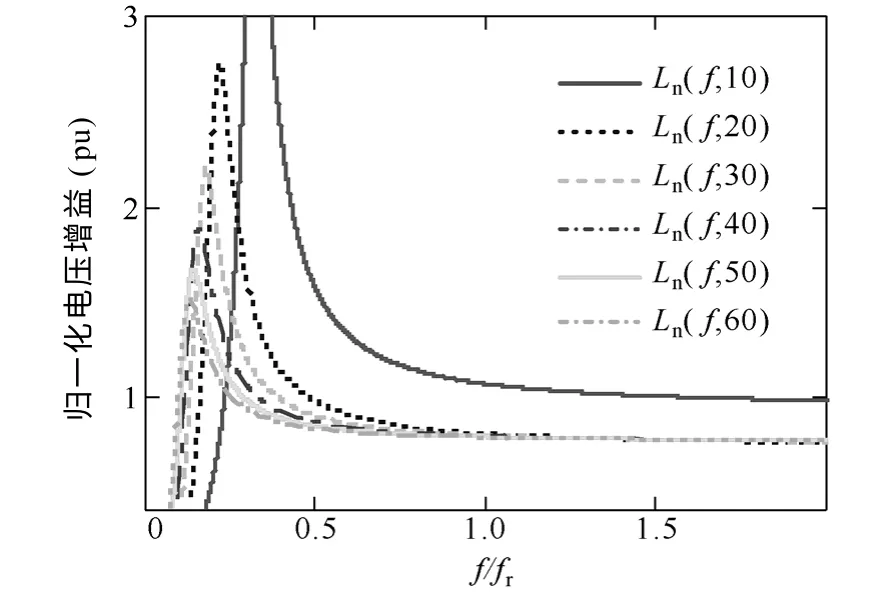
图8 LLC 不同Ln下的增益曲线Fig.8 Gain characteristic of LLC converter on the different Ln

LLC-DCT 作为中转母线变换器时，通常为48V转12V，输出低压且电流较大时负载RL的阻值很小，由式（17）可知由此可能会造成Q值偏大。以本文中样机为例，主变压器采用平面变压器，使用变压器漏感来充当谐振电感，变压器漏感为0.61μH，谐振电容为166nF，如果负载电阻RL为0.6Ω。那么这时Q值计算得

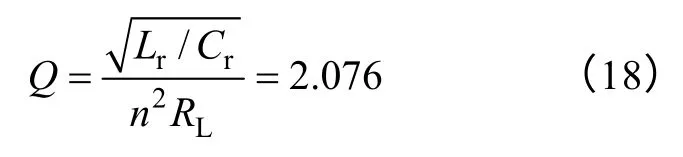
图9 所示是一组Ln固定、不同Q值下的增益曲线，可以看出Q值为2.076 时，其增益曲线特性非常软，如果开关频率与谐振频率稍有差别会导致输出电压掉落。解决这个问题的方法一是合理设计平面变压器，使得变压器的磁路耦合加强，漏感减小，使得Q值减小；二是使用谐振频率跟踪技术[12-15]，使得开关频率一直工作在谐振频率处。

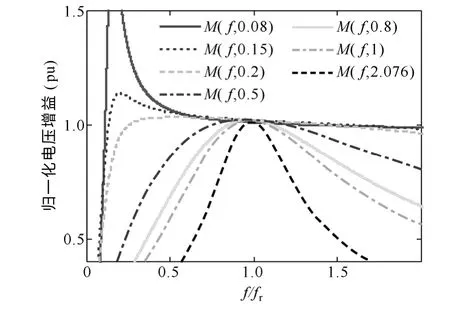
图9 LLC 在不同Q 值下的增益曲线Fig.9 Gain characteristic of LLC converter on the different Q

4 实验验证

为了验证以上结论，设计了一台LLC-DCT 样机作为中转母线变换器，输入48V，输出12V，满载150W，体积为标准1/4 砖。谐振频率为500kHz，漏感 0.61μH，同时作为谐振电感，谐振电容为166nF，控制采用TI 公司的DspF28027。如图10 所示，为实验样机照片。图11 所示的是两组不同死区时间下的工作波形。

图10 实验样机照片Fig.10 Converter prototype

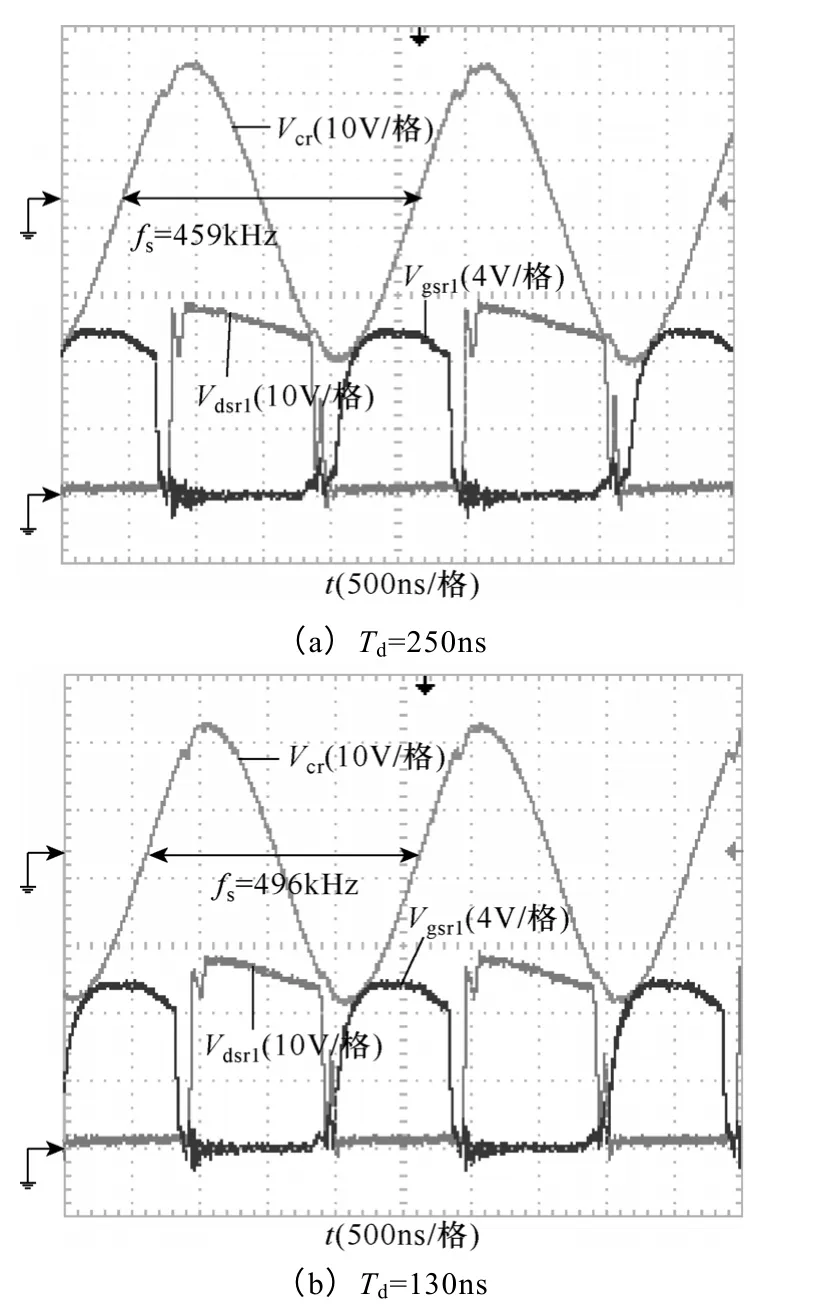
图11 不同死区时间下的工作波形Fig.11 The experimental curve on the different dead time

为了验证设计正确性，做了对比性实验，设置了三组死区时间Td和其对应的Lm值，见下表。其三组效率随输出功率变化曲线如图12 所示。

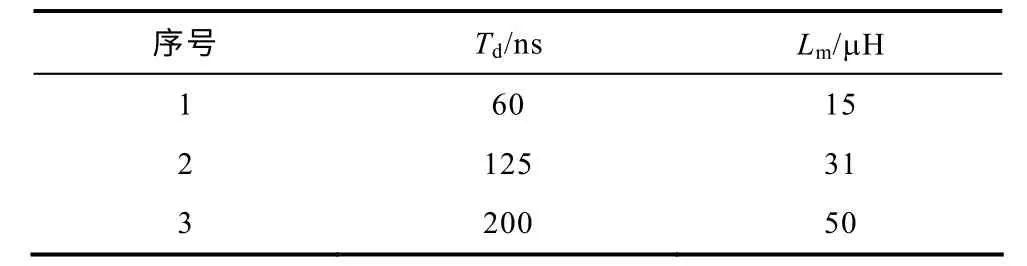
表 3组对照实验Td与Lm值Tab.The value of Tdand Lmon three comparative experiments

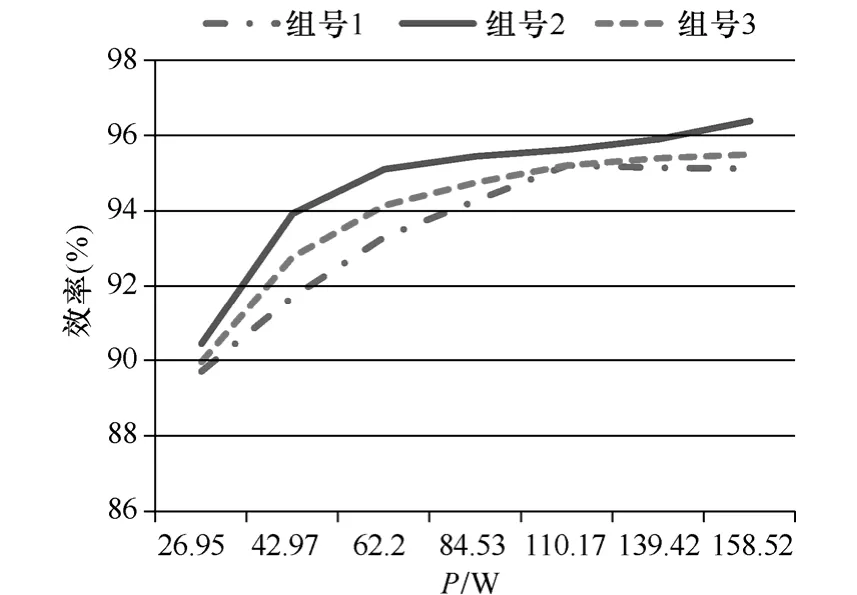
图12 LLC-DCT 在3组Td值下的效率曲线Fig.12 The efficiency curve of LLC-DCT on three comparative experiments

从图12 可以看出，组号2 在全负载范围内的效率均比其他两组高，可以说明以上述设计方法设计的死区时间和励磁电感可以使得LLC 谐振变换器总损耗得到最小化，从而获得较优的效率。

5 结论

本文研究了一种基于死区时间Td和励磁电感Lm最优解的LLC 谐振参数设计方法。通过最佳死区时间和励磁电感选取，得到最优化整机效率，并针对LLC-DCT 的特点，对Ln和Q值的选取进行了讨论，得出了Ln越大，Q值越小，越有利于LLC-DCT 维持稳定直流增益的结论。最后设计一台150W 的中转母线变换器，对以上结论进行了验证。

[1]Lu Bing,Liu Wenduo,Liang Yan,et al.Optimal design methodology for LLC resonant converter[C].IEEE Applied Power Electronics Conference and Exposition,2006:553-538.

[2]Yu Ruiyang,Ho Godwin Kwun Yuan,Pong Bryan Man Hay,et al.Computer-aided design and optimization of high-efficiency LLC series resonant converter[J].IEEE Transaction on Power Electronics,2012,27(7):3243-3256.

[3]王镇道,赵亚魁,章兢.LLC 半桥式谐振变换器参数模型与设计[J].电工技术学报,2012,27(12):51-54.Wang Zhendao,Zhao Yakui,Zhang Jing,et al.Parameter model and design for LLC resonant halfbridge converter[J].Transactions of China Electrotechnical Society,2012,27(12):51-54.

[4]陈申,吕征宇,姚玮.LLC 谐振型软开关直流变压器的研究与实现[J].电工技术学报,2012,27(10):163-167.Chen Shen,Lü Zhengyu,Yao Wei.Research and verification on LLC resonant soft switching DC-DC transformer[J].Transactions of China Electrotechnical Society,2012,27(12):163-167.

[5]Adragna C,De Simone S.Designing LLC resonant converters for optimum efficiency[C].13th European Conference on Power Electronics and Applications,2009:1-10.

[6]Yu Ruiyang,Ho Godwin,Kwun Yuan,et al.Computeraided design and optimization of high-efficiency LLC series resonant converter[J].IEEE Transaction on Power Electronics,2012,27(7):3243-3256.

[7]Sihun Yang,S Shoyama M.Parametric analysis of LLC resonant converter using flat transformer for loss reduction[C].14th International Power Electronics and Motion Control Conference,2010,T2-204-T2-209.

[8]Fang Y,Xu D,Zhang Y,et al.Design of high power density LLC resonant converter with extra wide input range[C].Twenty-Second Annual IEEE Applied Power Electronics Conference,APEC 2007:976-981.

[9]Lee J Y,Jeong Y S,Chae H J,et al.Two-stage insulated bidirectional DC/DC power converter using a constant duty ratio LLC resonant converter:U.S.,2011/0090717A1[P].2011-4-21.

[10]Ryu B W,Moon G W,Choi S W,et al.Adapter power supply:U.S.,2012/0069603A1[P].2012-3-22.

[11]Vinciarelli P.Factorized power architecture with point of load sine amplitude converters:U.S.,6984965B2[P].2006-01-10.

[12]Zwerver H J.Automatic frequency control for series resonant switched mode power supply:U.S.,2009/0115381A1[P].2009-03-07.

[13]Weiyi Feng,Paolo Mattavelli,Fred C Lee.Pulse width locked loop (PWLL) for automatic resonant frequency tracking in LLC DC-DC transformer (LLCDCX)[J].IEEE Transaction on Power Electronics,2013,28(4):1862-1869.

[14]Heng H,Pei Y,Yang X,et al.Frequency tracking control for cap-charging parallel resonant converter with phase-locked loop[C].Proceedings of IEEE Applied Power Electronics Conference,2007:1287-1292.

[15]Yan Y,Shirazi M,Zane R.Electronic ballast control IC with digital phase control and lamp current regulation[J].IEEE Transaction on Power Electronics,2008,23(1):11-18.