一种零电压转换双升压有源功率因数校正变换器

胡 玮 康 勇 周小宁 王学华

（1.华中科技大学 强电磁工程与新技术国家重点实验室 武汉 430074 2.武汉全华光电科技有限公司 武汉 430070）

1 引言

无桥升压功率因数校正（Boost Power Factor Correction,Boost PFC）变换器相较普通Boost PFC变换器可通过减少整流二极管数量来降低了导通损耗，提高了变换器效率，近年来得到越来越多的研究[1-3]。但普通无桥Boost PFC 变换器由于升压电感的位置在交流测，高频工作状态下线间寄生电容使得变换器的共模噪声急剧变大[4-6]，产生严重的电磁干扰（Electromagnetic Interference，EMI）。一般情况下，大功率无桥Boost PFC 变换器须配备多级EMI 滤波器，导致其功率密度大幅度下降，限制了其在工业领域的推广使用。针对上述问题，文献[7-9]提出了一种含回路二极管的双升压有源功率因数校正（Dual Boost Power Factor Correction,DBPFC）变换器拓扑，电路增加了两个回路二极管VDa和VDb（慢恢复二极管）与输入电压vin建立联系，在输入电压（频率为工频）正负半周期交替开通，大幅降低了变换器的共模干扰。

无桥 Boost PFC 变换器拓扑仅降低了导通损耗，对于降低开关损耗，目前的研究主要集中在软开关技术上。在无源软开关技术研究方面，文献[10]提出了一种无桥软开关 Boost PFC 变换器拓扑，两对谐振电感和电容在主开关管开通和关断时刻谐振，实现了开关管的零电流开通和升压二极管的自然关断；文献[11]提出了另一种无桥软开关 Boost PFC 变换器拓扑，通过采用耦合电感，实现了开关管的零电流开通、零电压关断和升压二极管的自然关断。无源软开关技术的主要局限在于由于没有辅助开关管控制，谐振电感和电容在整个开关周期均工作，额外损耗大，使得整体效率提升均不显著。同时，在其工作频率范围内，电压、电流应力会受到谐振器件参数的约束。在有源软开关技术研究方面，目前零电压转换（Zero-Voltage Transition,ZVT）技术被认为是最优选的方案，因为它可实现主开关管的零电压开关（Zero-Voltage Switching,ZVS）和升压二极管的自然开关，并且不增加各开关器件的电压应力。文献[12-14]提出了一种ZVT Boost PFC变换器拓扑，可实现主开关管的ZVS和升压二极管的自然开关，但该拓扑的辅助开关管是硬关断，使得变换器整体效率提升不理想；文献[15]提出了一种适用于无桥Boost PFC 主电路的ZVT Boost PFC变换器拓扑；文献[16-18]通过在文献[12]的变换器拓扑上增加一些饱和电感或耦合电感来改善辅助开关管的关断特性，降低变换器的EMI，但这一系列拓扑均增加了系统的成本和复杂性；文献[19-21]在文献[12]的变换器拓扑上增加了一个谐振电容，即实现了辅助开关管的零电压关断，改善了关断特性，提高了效率。

综合以上文献的优点，本文研究了一种 ZVT DBPFC 变换器，该变换器可以实现主开关管的ZVS和升压二极管的自然开关，与此同时实现辅助开关管的零电流开通和零电压关断，大幅减少了开关管开关损耗和升压二极管反相恢复损耗，提高了系统效率，同时并未增大各开关器件的电压应力。本文对该变换器拓扑在一个开关周期内的工作模态进行理论分析，详细讨论了软开关实现条件和控制策略并给出了主要仿真波形。最终完成了一台开关频率100kHz，输出功率600W 的平均电流控制方式的原理样机，验证了理论分析的正确性。

2 工作原理

2.1 拓扑结构分析

本文提出的ZVT DBPFC 变换器由含回路二极管的DBPFC 变换器和有源辅助谐振支路组成。其中含回路二极管的DBPFC 变换器是主电路，升压电感L1、L2，升压二极管VD1，主开关管S1、S2与回路二极管VDb构成输入电压vin工频正半周期的主电路拓扑；升压电感L2、L1，升压二极管VD2，主开关管S2、S1与回路二极管VDa构成输入电压vin工频负半周期的主电路拓扑。谐振电感Lr，辅助开关管Sr，谐振电容Cr，连通二极管VD3、VD4、VD5和VD6与主开关管并联谐振电容CS1、CS2构成有源辅助谐振支路。C0为输出滤波电容，R0为等效负载电阻。ZVT DBPFC 变换器本质是两路相同拓扑的单管Boost PFC 变换器和有源辅助谐振支路在输入电压正负半周期分别工作。其变换器拓扑如图1所示。

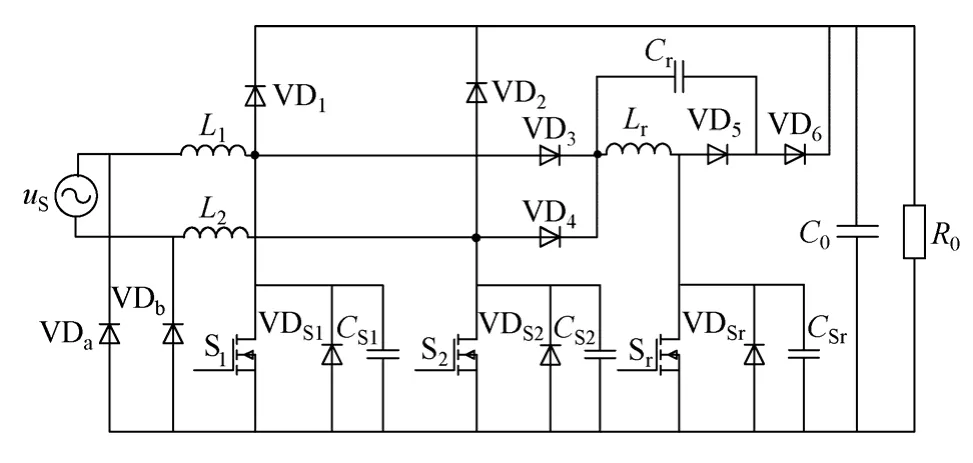
图1 ZVT DBPFC 变换器拓扑Fig.1 The topology of the ZVT DBPFC converter

2.2 工作模态分析

为方便分析，不考虑各开关管和二极管开通时间、导通压降等问题，也不考虑辅助开关管的寄生二极管和寄生电容对变换器工作模态的影响。由于S1和S2在输入电压vin正、负半周期交替工作，工作过程是完全对称的，故仅分析vin正半周期输入时变换器的工作模态，此时，电感电流iL1（即输入电流）的返回路径是流经通路二极管VDb和不工作的主开关管S2的体二极管VDS2。在任一开关周期内，升压电感L1可以作为一个恒定的电流源IL1，输出电容C0可以作为一个恒定的电压源V0。ZVT DBPFC 变换器关键波形如图2 所示。波形从上到下依次为S1的驱动信号vg1；Sr的驱动信号vgr；Lr的电流iLr；S1的漏-源电压vS1和电流iS1；VD1的电压vVD1和电流iVD1；Sr的漏-源电压vSr和电流iSr；Cr的电压vCr；VD6的电流iVD6。

具体工作模态分析如图3 所示[22,23]。

模态1[t7～t0]：在t0时刻之前，有源辅助谐振支路未工作，主开关管S1、辅助开关管Sr均关断。由于升压电感L1的存在，IL1可以认为大小不变，在此模态下，iVD1=IL1，vS1=V0。

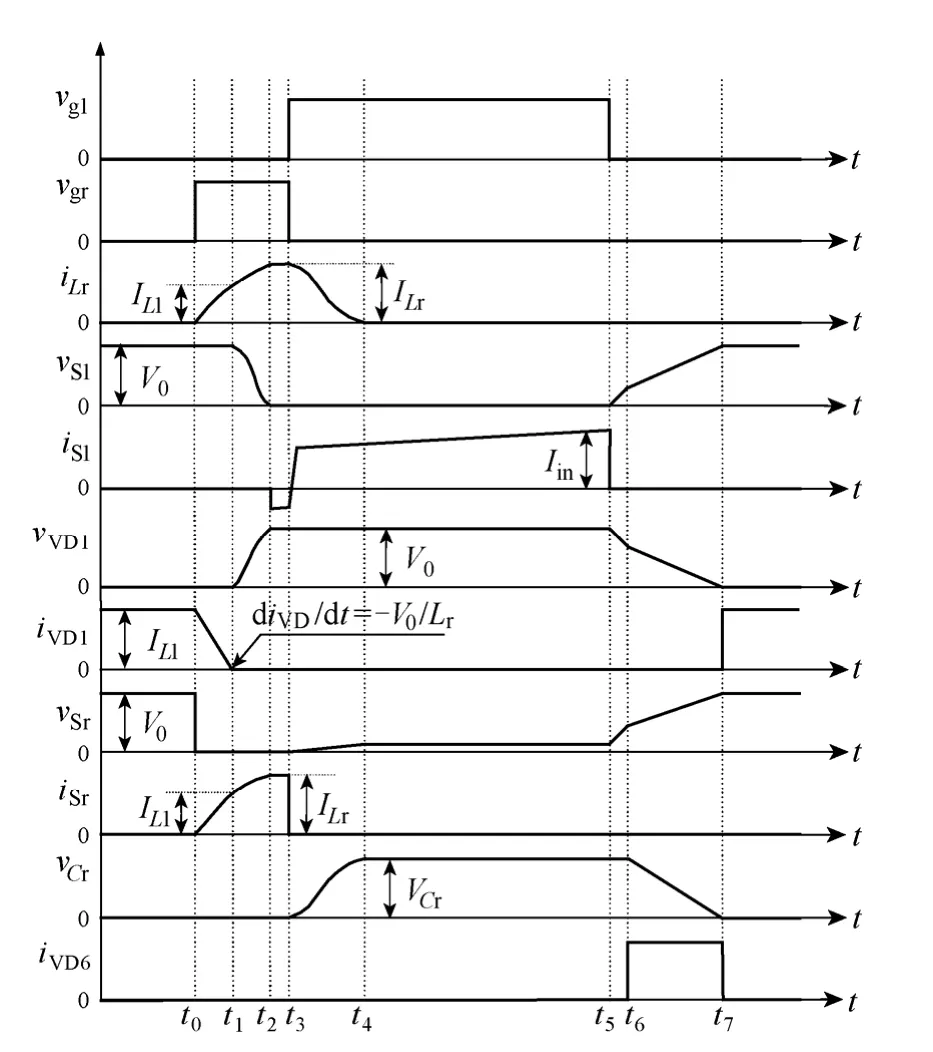
图2 ZVT DBPFC 变换器关键波形Fig.2 Key waveforms of the ZVT DBPFC converter

模态2[t0～t1]：在t0时刻开始模态2，此时Sr导通，由于谐振电感Lr的存在，Sr的电流不能突变，Sr是零电流开通的，VD3自然开通。在此模态下，随着iLr的不断增加，iVD1不断减小，直到iLr达到IL1，升压二极管VD1自然关断。有方程

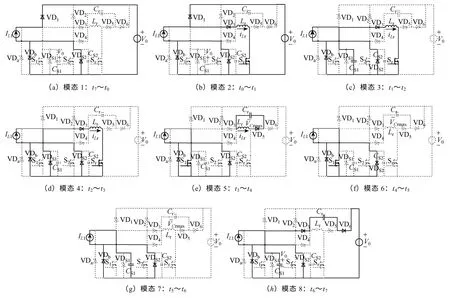
图3 ZVT DBPFC 变换器模态分析Fig.3 Operating modes of the ZVT DBPFC converter

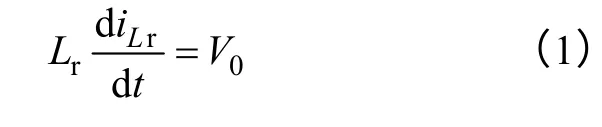
约束条件为

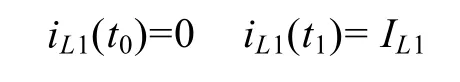
此模态持续时间为

模态3[t1～t2)：在t1时刻开始模态3，此时iVD1=0，VD1自然关断，而S1尚未开通，vVD1仍为零，VD1反向恢复损耗接近为零。在此模态下，vS1(t1)=V0，Lr与S1两端的并联电容CS1开始谐振，CS1开始放电，iLr继续增大。有方程

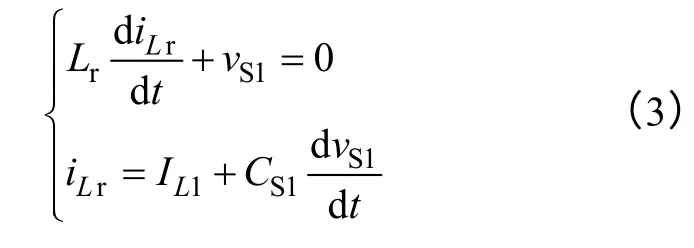
约束条件为

可解得

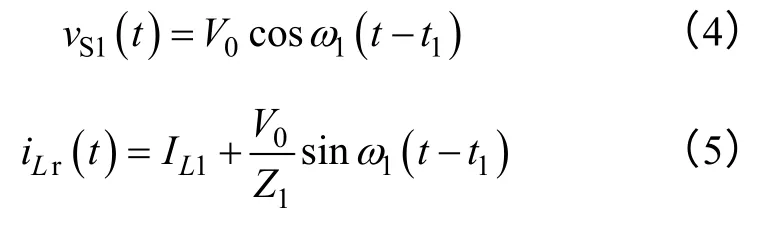
式中

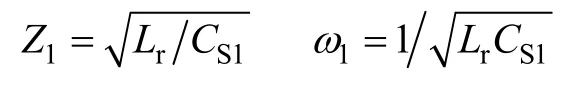
此模态持续时间为

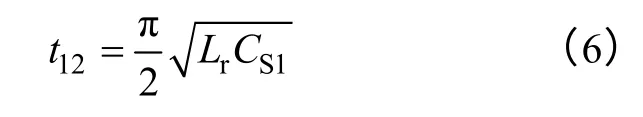
模态4[t2～t3]：在t2时刻开始模态4，此时vS1=0，iLr达到此开关周期电流最大值ILr=IL1+V0/Z1，S1的体内反并二极管VDS1开通，维持S1的反向电流iS1。在此模态下，iLr继流，且维持在iLr=ILr，S1达到零电压开通条件。

模态5[t3～t4]：在t3时刻开始模态5，此时Sr关断，S1零电压开通，开通损耗很小；由于谐振电容Cr的存在，Sr的电压不能突变，其关断特性好，近似于零电压关断，VD3自然关断。在此模态下，Lr与Cr开始串联谐振，VD5自然开通。有方程如下：

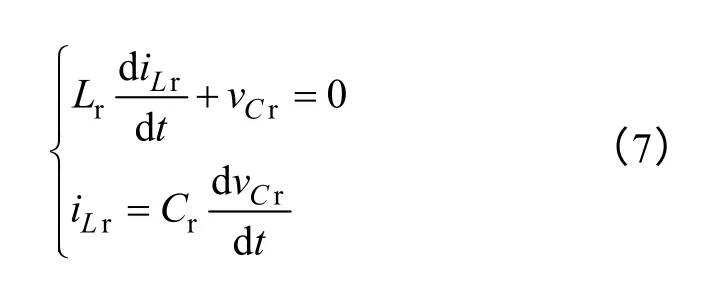
约束条件为

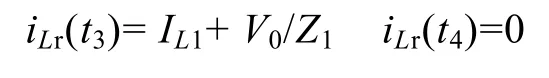
可解得

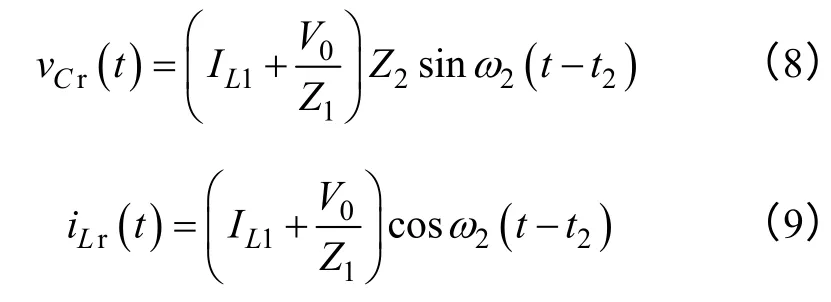
其中

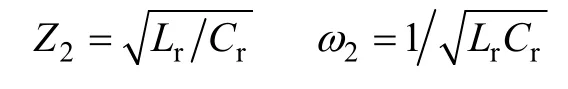
此模态持续时间为

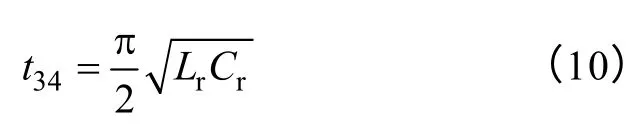
Lr通过串联谐振将其存储的能量传递给Cr，在t4时刻，vCr达到此开关周期的电压最大值

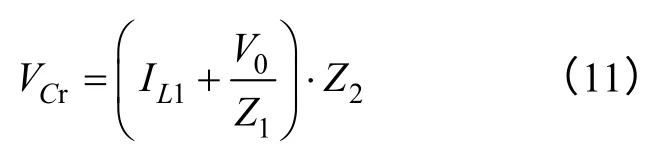
如果VCr≥V0，则vCr被钳位在V0。

模态6[t4～t5)：在t4时刻开始模态6，此时Lr与Cr谐振结束，iLr=0，VD5自然关断，有源辅助谐振支路不工作。在此模态下，含回路二极管的DBPFC主电路继续工作。

模态7[t5～t6)：在t5时刻开始模态7，此时S1关断，由于CS1的存在，S1是零电压关断的，关断损耗远小于硬关断。在此模态下，IL1对CS1充电。有方程

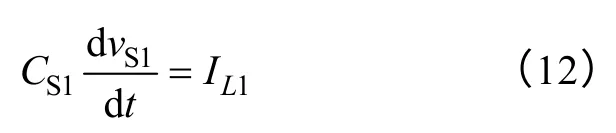
约束条件为

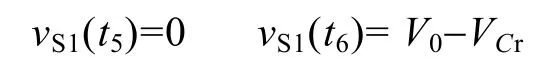
此模态持续时间为

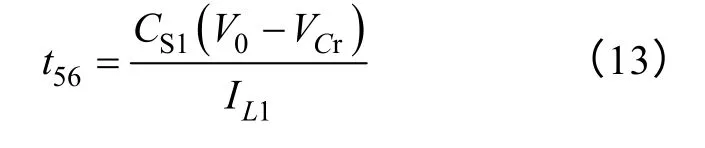
模态 8[t6～t7)：在t6时刻开始模态 8，此时vS1+VCr=V0。在此模态下，CS1继续充电，同时Cr开始放电，VD3、VD6自然开通。有方程

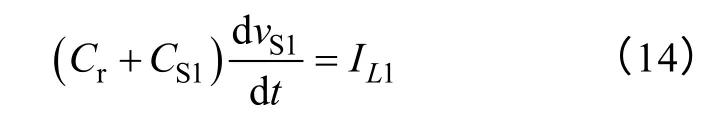
约束条件为

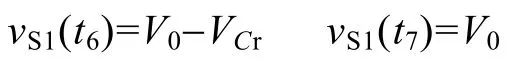
此模态持续时间为

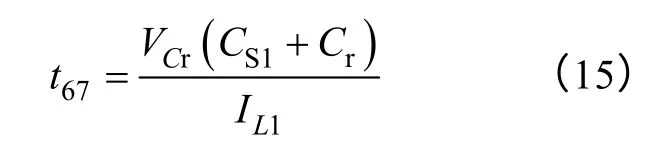
到t7时刻，CS1充电结束，vS1=V0，同时Cr放电结束，vCr=0，VD3、VD6自然关断，VD1自然开通，电路回到下一个开关周期过程。

3 电路讨论

3.1 软开关实现条件

通过主开关管与辅助开关管的交错开通，可实现主开关管S1、S2的ZVS。以S1为例，在S1关断时，CS1限制了S1的电压上升率，自然实现了S1的零电压关断；而在S1开通时，必须要将CS1上的电荷释放到0，即vS1=0，才能实现零电压开通。

谐振电感Lr在一个开关周期中参与两次谐振，在主开关管S1开通前，Lr首先与CS1串联谐振，将CS1上的电荷释放到0；在辅助开关管Sr关断时，Lr与Cr串联谐振，将储存的能量转移到Cr中，并最终释放到负载中。由此得出ZVT DBPFC变换器实现软开关的两个约束条件，首先辅助开关管Sr的开通时间tSr必须保证通过谐振，CS1中存储的能量完全被释放，即

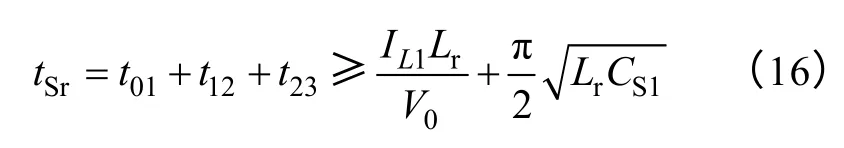
式（16）中t23时间很短，可以忽略。只有满足此条件时，才能实现S1开通时CS1存储的能量已完全释放。其次，Lr与Cr串联谐振，将储存的能量转移到Cr中的时间要比S1的开通时间短，保证Lr将能量完全转移到Cr中，并在S1关断后进一步将Cr的能量释放到负载中。

3.2 控制策略

ZVT DBPFC 变换器只能工作在电感电流连续模式（Continuous Current Mode,CCM），平均电流法在CCM 模式下能有效地减小跟踪误差产生的畸变，故对ZVT DBPFC 变换器采用平均电流法进行控制，控制芯片采用UC3854。通过一个由R1和C1组成的脉冲移相电路和一个若干门电路组成的逻辑控制电路产生电压驱动信号vg1、vg2和vgr，其中脉冲移相电路的移相时间即为辅助开关管的开通时间tSr，即tSr=R1C1，tSr需满足式（16）。同时逻辑控制电路使S1、S2与Sr交错开通，ZVT DBPFC 变换器系统电路如图4 所示。

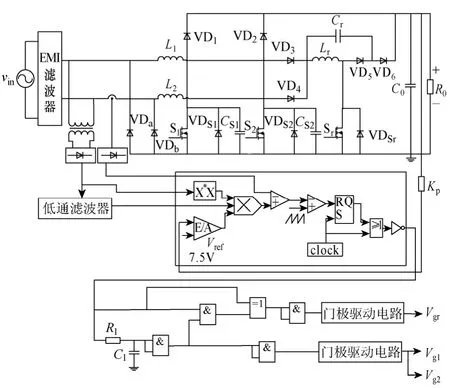
图4 ZVT DBPFC 系统电路图Fig.4 System circuit diagram of the ZVT DBPFC

3.3 有源辅助谐振支路参数设计

ZVT DBPFC 变换器的有源辅助谐振支路参数设计主要考虑在最小电压输入（Vinmin=90V），额定输出时的情况。设定η≈0.9，此时最大电感电流有效值为IL1rms=P0/(Vinminη)=7.5A，最大电感电流峰值为IL1max=10.5A。

3.3.1 谐振电感的设计

当iL1达到电感电流峰值IL1max时，t01达到最大值。为了减少有源辅助谐振支路的导通损耗，本文设定其开通时间为开关周期TS的1/10，即

进而得出谐振电感Lr的取值范围

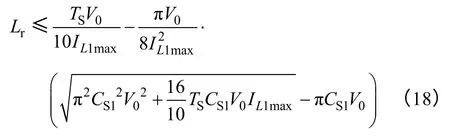
流过Lr的最大峰值电流ILrmax为

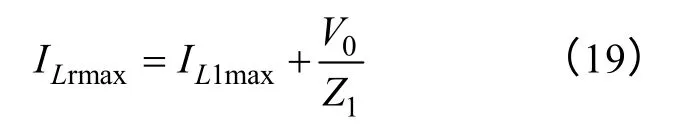
流过Lr的最大有效值电流ILrmax为

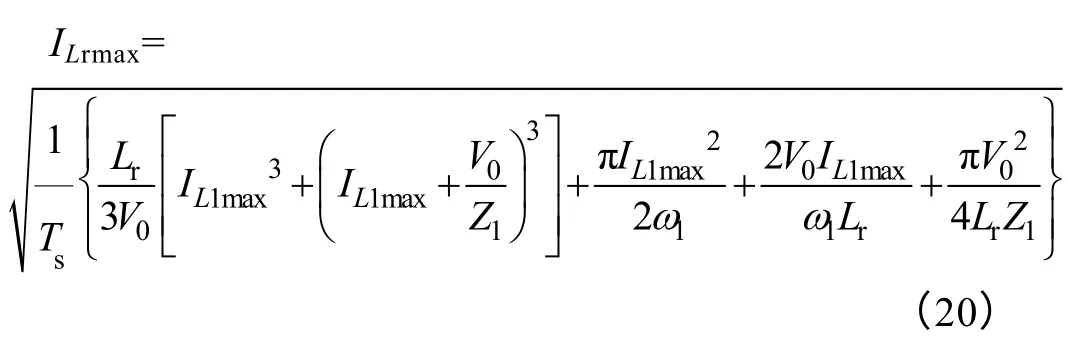
3.2.2 谐振电容的设计

谐振电容CS1作为S1的缓冲电容，使得vS1的上升率不要太快，以降低S1的关断损耗。本文选择在最小电压输入、额定输出时，vS1从0 上升到V0的时间为S1关断时间toff的2 倍，即

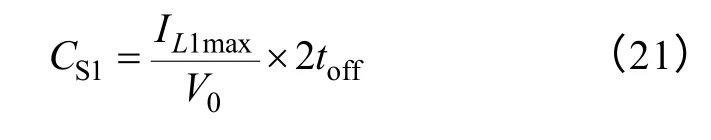
Cr同时作为S1和Sr关断时的缓冲电容，以降低S1和Sr的关断损耗。但S1的电流定额更大，在选择Cr时，主要考虑S1的关断特性，使得Cr在放电时速度不要太快。本文选择在最小电压输入，额定输出时，vCr从VCr下降到0 的时间为S1关断时间toff的10 倍，即

3.3.3 辅助开关管的选择

流过辅助开关管Sr的最大电流峰值与流过谐振电感Lr的最大电流峰值相同，均为

Sr的最大电流有效值为

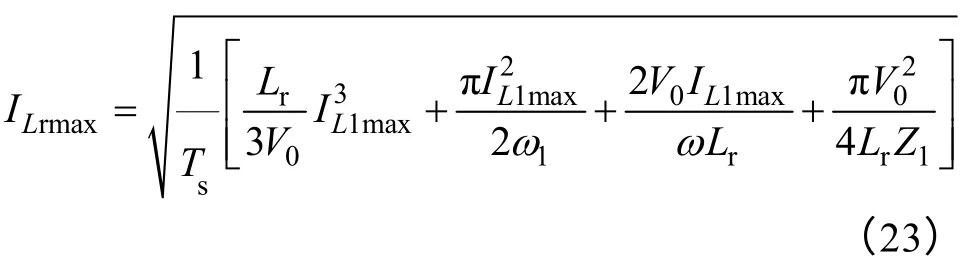
Sr所承受的最大电压为V0。

4 仿真研究

本文对ZVT DBPFC 变换器进行了Saber 仿真研究，仿真条件为：输入电压220V、50Hz，输出电压400V，额定输出功率600W，开关频率100kHz。升压电感L1、L2取值为0.5mH，谐振电感Lr取值为8.1μH，谐振电容CS1、CS2取值为2nF，Cr取值为10nF，输出电容C0取值为1 120μF。图5 为主要仿真波形，其中图5a 为S1的驱动信号vg1，图5b 为Sr的驱动信号vgr，图5c 为L1的电流iL1和Lr的电流iLr，图5d 为S1的漏-源电压vS1，图5e 为VD1的电压vVD1，图5f 为VD1的电流iVD1，图5g 为Sr的漏-源电压vSr，图5h 为Sr的电流iSr，图5i 为Cr的电压vCr，图5j 为Cr的电流iCr。

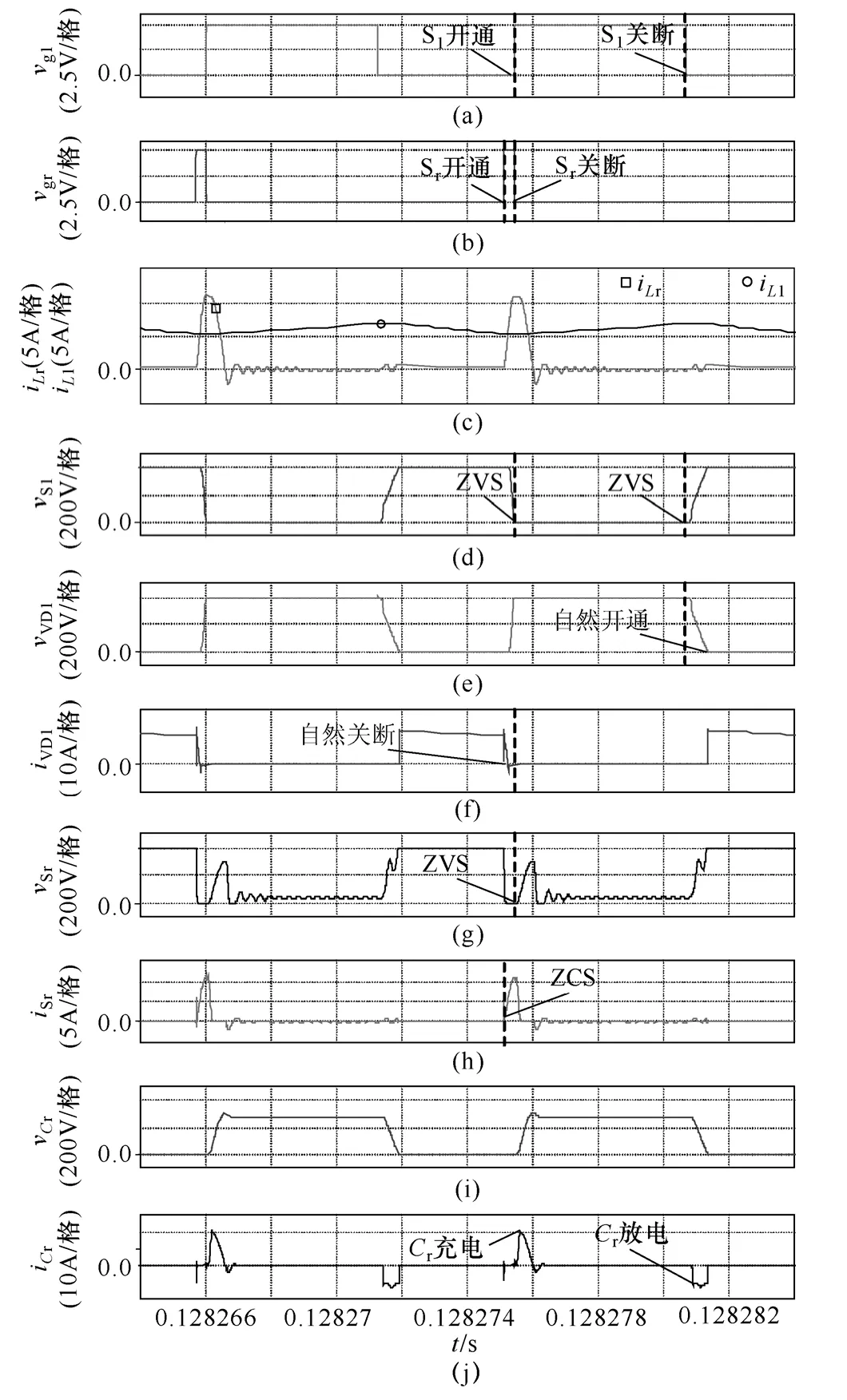
图5 ZVT DBPFC 变换器仿真波形Fig.5 Simulation waveforms of the ZVT DBPFC converter

图5c 显示Lr的工作时间只占一个开关周期的一小部分，有源辅助谐振支路的导通损耗非常小；iL1在一个周期内基本维持不变，可认为是一个恒定的电流源IL1。图5d 显示当S1开通时，有源辅助谐振支路已使vS1下降到零，并且VDS1已开通，因此S1是零电压开通的；而当S1关断时，CS1限制了vS1的上升率，电压缓慢上升，因此S1是零电压关断的。图5e 显示当S1关断时，CS1限制了vVD1的下降率，其电压缓慢降低到零，因此VD1是自然开通的。图5f 显示当S1开通时，iVD1已下降为零，因此VD1不存在反向恢复损耗，是自然关断的。图5g 显示当Sr关断时，Cr限制了vSr的上升率，电压缓慢上升，因此Sr是零电压关断的。图5h 显示当Sr开通时，Lr限制了iSr的上升率，电流缓慢上升，因此Sr是零电流开通的。图5i和图5j 显示Cr在一个开关周期内充放电一次。当Sr关断时，Cr充电，它作为Sr的缓冲电容，使得Sr零电压关断；当S1关断时，Cr放电，它与CS1并联作为S1的缓冲电容，使得S1零电压关断。

5 实验验证

为验证理论分析和仿真结果的正确性，设计并搭建了ZVT DBPFC 变换器原理样机，实验条件与仿真条件相同，主开关管S1、S2和辅助开关管Sr选用IRFP460；升压二极管VD1、VD2和通路二极管VD3、VD4、VD5、VD6选用MUR1560；回路二极管VDa、VDb选用HER606；谐振电感Lr磁心选取铁硅铝磁环 MS-130026-2，μ=26 绕制。考虑到IRFP460 的结电容约为500pF，CS1、CS2选取1.5nF，其与Cr均选取高频瓷片电容。

图6 显示在输入电压220V，输出电压400V，输出功率600W 的情况下输入电压vin与电感电流iL1的波形；iL1的波形显示ZVT DBPFC 变换器具有很高的功率因数和较低的总谐波失真（Total Harmonic Distortion,THD），达到了功率因数校正的目的。

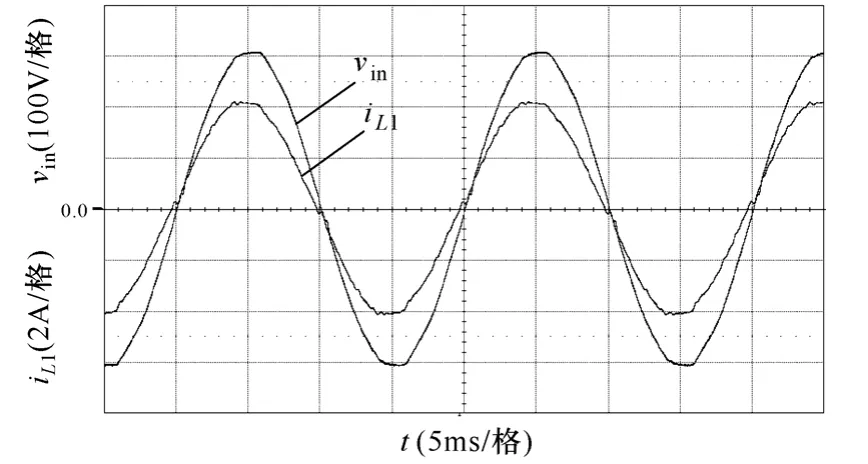
图6 额定电压满载时输入电压和电感电流波形Fig.6 Measured key waveforms of the input voltage and the inductor current at rated voltage and full load

图7显示了S1、VD1和Sr的电压、电流的波形，其中虚线部分为电压、电流交叠区，即开关损耗出现时刻。图7a显示S1实现了零电压开通，即在S1开通前，iS1反向通过S1的体二极管VDS1，其电压、电流交叠区为0，开通损耗为0；同时S1实现了零电压关断，其电压、电流交叠区很小，关断损耗大幅减小。图7b显示VD1实现了自然导通，其电压、电流交叠区很小，开通损耗大幅减小；同时VD1实现了自然关断，即在iVD1下降为0时，vVD1才开始上升，不存在反向恢复问题，关断损耗为0。图7c显示了Sr实现了零电流开通，其电压、电流交叠区很小，开通损耗大幅减小；同时Sr实现了零电压关断，其电压上升率和幅值都受到了限制，电压、电流交叠区非常小，关断损耗基本为0。

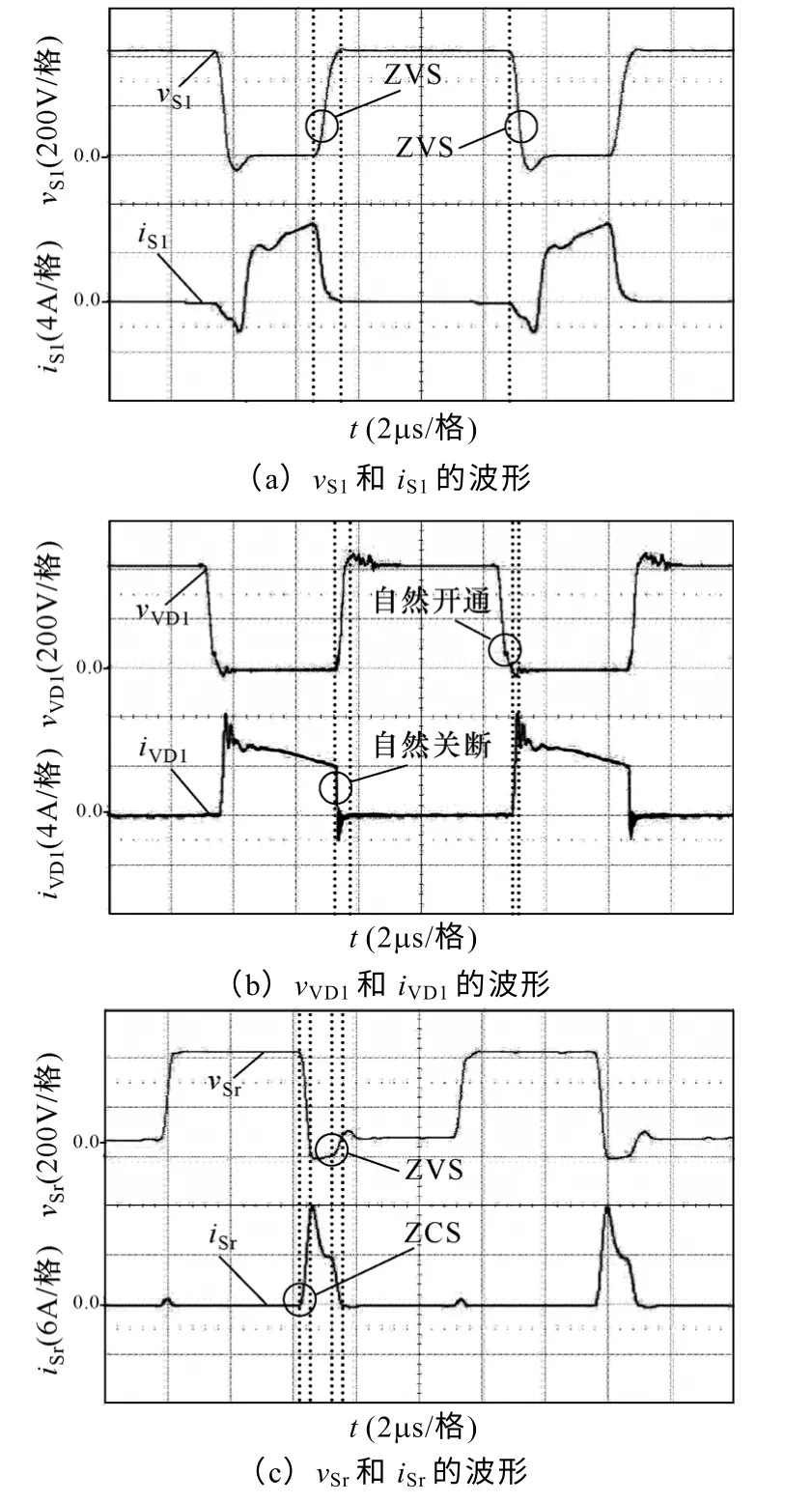
图7 各开关管和升压二极管的电压电流波形Fig.7 Measured key waveform of voltages and currents of the switchs and the Boost diode

图8 显示了在一个开关周期中谐振电感Lr的电流波形，驱动信号vg1和vgr驱动S1和Sr交错开通，Lr在Sr上升沿与CS1谐振储能，iLr从零上升至此开关周期电流最大值ILr；随后在下降沿与Cr谐振放电，iLr在Sr关断前从ILr下降至0。

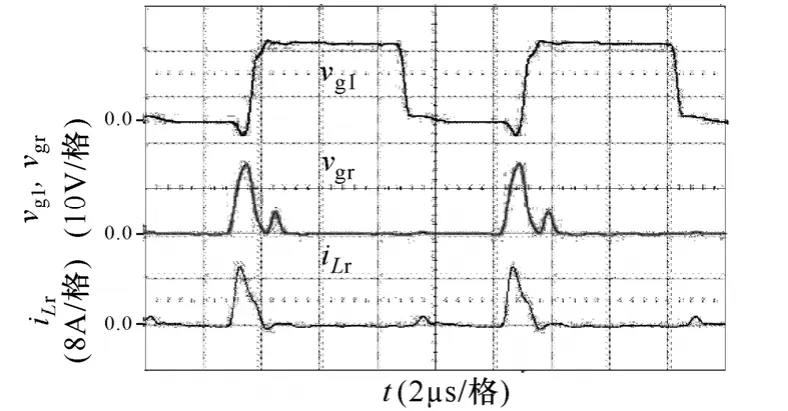
图8 谐振电感的电流波形Fig.8 Measured key waveforms of current of the resonant inductor

图9 显示了在一个开关周期中谐振电容Cr的电压、电流波形。当Sr关断时，Cr吸收Lr的电量，vCr从0 增加到此开关周期最大值VCr；当S1关断且vS1增加至vS1=V0-VCr时，Cr开始将存储电量释放到负载，vCr从VCr下降至0。iCr波形显示了Cr的充放电过程。

图9 谐振电容的电压电流波形Fig.9 Measured key waveforms of voltage and current of the resonant capacitor

图9 显示了ZVT DBPFC 样机与文献[7]提出的硬开关DBPFC 样机和文献[22]提出的ZVZCS 样机的效率对比曲线，比较条件是样机输出功率为600W，输入电压在85～265V 之间变化。实验证明本文提出变换器的开关损耗和导通损耗均非常低，取得了最佳的效率曲线，效率峰值均达到了96.7%。相较硬开关 DBPFC 样机，电路提升效率 1.2%～2.2%，显示有源辅助谐振支路大幅降低了开关损耗；相较ZVZCS 样机，电路提升效率0.6%～1.0%，显示含回路二极管的 DBPFC 主电路相较于传统Boost PFC 主电路降低了导通损耗。特别在低电压大电流输入的情况下，二极管的反向恢复更严重，效率提升更明显，随着输入电压的增加，效率提升逐渐减小并趋于稳定。

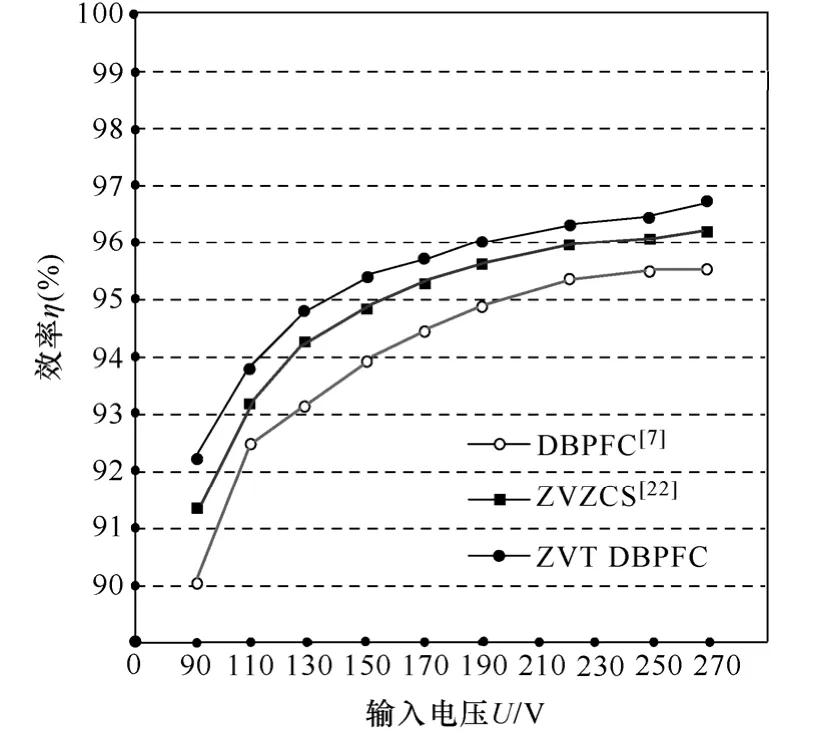
图10 满载时电路效率随输入电压的变化曲线Fig.10 Measured power efficiencies with relation to the input voltage at full load

硬开关DBPFC 变换器的EMI 远小于普通无桥PFC 变换器，与传统Boost PFC 变换器相等[11]，而相较于硬开关DBPFC 变换器，ZVT DBPFC 变换器大幅改善了功率器件的电压变化率dv/dt和电流变化率di/dt，EMI 得到了进一步降低。针对dv/dt和di/dt与EMI 之间的关系，文献[21]给出了分析，本文不再详细讨论。

6 结论

本文提出了一种ZVT DBPFC 变换器，该变换器通过在含回路二极管的DBPFC 主电路中增加一个有源辅助谐振支路，提高了工作效率。本文详细讨论了主开关管和升压二极管实现软开关的条件并给出了有源辅助谐振支路的参数设计。理论分析和实验证明了变换器可以实现主开关管的ZVS和升压二极管的自然开关，与此同时实现了辅助开关管的零电流开通和零电压关断，大幅减少了开关管的开关损耗和升压二极管的反相恢复损耗。工作效率对比分析显示该变换器能显著提升工作效率，同时解决了普通无桥PFC 变换器EMI 较高的缺点，在实际应用中具有良好的可推广性。

[1]王玉斌,厉吉文,田召广,等.一种新型的基于单周控制的功率因数校正方法及实验研究[J].电工技术学报,2007,22(2):137-143.Wang Yubin,Li Jiwen,Tian Zhaoguang,et al.A new PFC method and experimental study based on onecycle control[J].Transactions of China Electrotechnical Society,2007,22(2):137-143.

[2]王议锋,徐殿国,徐博,等.图腾柱式无桥零纹波交错并联Boost 功率因数校正器[J].电工技术学报,2011,26(9):175-182.Wang Yifeng,Xu Dianguo,Xu Bo,et al.An interleaved totem-pole bridgeless Boost PFC rectifier with zeroripple current filter[J].Transactions of China Electrotechnical Society,2011,26(9):175-182.

[3]Gopinath M,Prabakaran,Ramareddy S.A brief analysis on bridgeless boost PFC converter[C].Sustainable Energy and Intelligent Systems,Chennai,India,2011:242-246.

[5]Kong Pengju,Wang Shuo,Lee F C.Common mode EMI noise suppression in bridgeless Boost PFC converter[C].Applied Power Electronics Conference,Anaheim,CA,USA,2007:929-935.

[6]Ye Haoyi,Yang Zhihui,Dai Jingya,et al.Common mode noise modeling and analysis of dual Boost PFC circuit[C].Telecommunications Energy Conference,Shanghai,China,2004:575-582.

[7]Huber L,Jang Yungtaek,Jovanovic M M.Performance evaluation of bridgeless PFC Boost rectifiers[J].IEEE Transactions on Power Electronics,2008,23(3):1381-1390.

[8]胡玮,康勇,周小宁.一种含回路二极管双Boost PFC电路[J].电力电子技术,2013,47(7):61-63,98.Hu Wei,Kang Yong,Zhou Xiaoning.A dual Boost PFC circuit with return diodes[J].Power Electronics,2013,47(7):61-63,98.

[9]胡玮,康勇,王学华,等.一种改进型双升压功率因数校正电路[J].电机与控制学报,2013,17(3):40-48.Hu Wei,Kang Yong,Wang Xuehua.Improved dual Boost power factor correction converter[J].Electric Machines and Control,2013,17(3):40-48.

[10]Liu Yaoping,Smedley K.A new passive soft-switching dual-Boost topology for power factor correction[C].Power Electronics Specialist Conference,June 15-19,2003,Irvine,CA,USA,2003:669-676.

[11]王慧贞,张军达.一种新型无桥Boost PFC 电路[J].电工技术学报,2010,25(5):109-115.Wang Huizhen,Zhang Junda.A bridgeless Boost PFC converter[J].Transactions of China Electrotechnical Society,2010,25(5):109-115.

[12]Hua Guichao,Leu Chingshan,Jiang Yimin,et al.Novel zero-voltage-transition PWM converters[J].IEEE Transactions on Power Electronics,1994,9(2):213-219.

[13]Kanaan H Y,Sauriol G,Alhaddad K.Small-signal modeling and linear control of a high efficiency dual Boost single-phase power factor correction circuit[J].IEEE Transactions on Power Electronics,2009,2(6):665-674.

[14]Lu Di,Li Xiang,Liu Chen.PFC study based on ZVT-PWM soft switching technology[C].Power Electronics for Distributed Generation Systems,Hefei,China,2010:148-151.

[15]De Souza A F,Barbi I.A new ZVS-PWM unity power factor rectifier with reduced conduction losses[J].IEEE Transactions on Power Electronics,1995,10(6):746-752.

[16]Du Zhongyi,Zhao Guoyou.Development of the high power factor high efficiency soft-switching power supply for telecommunication application[C].Power Electronics and Motion Control Conference,Beijing,China,2000:473-475.

[17]Lin Jonglick,Yang Sungpei,Yu Chihhsiung.Averaged modeling of a ZVT soft switching PFC converter[C].Circuits and Systems,Tainan,2004:741-744.

[18]Lee I O,Lee D Y,Cho B H.High performance Boost PFC pre-regulator with improved zero-voltage-transition(ZVT) converter[C].Power Electronics Specialists Conference,Seoul,Korea,2002,3:1387-1391.

[19]Mahesh M,Panda A K.High-power factor three-phase ac-dc soft-switched converter incorporating zero-voltage transition topology in modular systems for high-power industry applications[J].IEEE Transactions on Power Electronics,2011,4(9):1032-1042.

[20]Tseng Chingjung,Chen Chernlin.Novel ZVT-PWM converters with active snubbers[J].IEEE Transactions on Power Electronics,1998,13(5):861-869.

[21]Zhu Julian,Ding Daohong.Zero-voltage-and zerocurrent-switched PWM DC-DC converters using active snubber[J].IEEE Transactions on Industry Applications,1999,35(6):1406-1412.

[22]阮新波,严仰光.直流开关电源的软开关技术[M].北京:科学出版社,2000.

[23]Wang Chienming.A novel zero-voltage-switching PWM Boost rectifier with high power factor and low conduction losses[J].IEEE Transactions on Industrial Electronics,2005,52(2):427-435.