基于Mie理论的激光雾中传输衰减特性研究*
魏海亮 邵利民 李茂林
(1.海军大连舰艇学院研究生管理大队 大连 116018)(2.海军大连舰艇学院军事海洋系 大连 116018)
1 引言
海雾是指海洋与大气相互作用特定条件下出现在海上或沿海地区上空低层大气中的一种凝结现象,是悬浮于大气边界层中大量水滴或冰晶使得水平能见度低于1km 的危险性天气现象[1]。海雾一般为平流雾,根据其水平能见度V的大小,等级可分为:1km<V<10km 为轻雾或霭、200m<V<500m 为大雾、50m<V<200m 为浓雾、V<50m 为重雾、当雾有滴水感时为雨雾。观测表明,雾滴半径通常在1μm~60μm 之间,在温度为正时大多数雾滴半径为7μm~15μm,温度为负时为2μm~5μm,平流雾雾滴平均直径一般在20μm。
随着激光技术的不断发展,其在军事领域的应用日益广泛,越来越多的激光设备装备于现代舰船,同时也将受到海雾环境的影响和制约。海雾对激光的影响主要是液态雾滴的吸收和散射,使其传输过程受到干扰、能量被衰减,导致激光设备不能发挥应有的效能。因此了解激光雾中传输特性,并准确快速预测其传输衰减对有效利用激光技术至关重要。本文将Mie散射理论应用于激光衰减计算中,并与其他经验衰减模型进行比较,同时分析了衰减系数随波长、能见度及温度的变化关系。
2 Mie衰减模型
由于雾滴粒子在空间取向的任意性和随机性,且粒子尺度较小,因此统计平均上将其看作各向同性的球形粒子进行分析。雾滴粒子的尺寸和激光波长差不多时,产生的散射可用Mie理论进行严格求解,因此Mie理论在研究激光雾中的传输特性方面有着广泛的应用。
根据Mie理论,消光系数定义如下
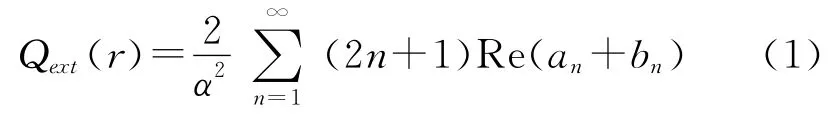
其中α=为尺度参数,r为粒子半径,λ为入射激光波长,n为本征值,an、bn为Mie系数。
目前被广泛使用的雾滴谱模型是两参数的Г分布(Khragian-Mazin分布)模型[2~3],其表达式为

a、b为确定雾滴谱分布的参数,当雾滴半径、能见度和含水量W分别以m、km 和g/m3为单位时,有以下关系[4]:

由于直接测量海雾含水量比较困难,通常用能见度来描述其的特征,平流雾含水量与能见度的经验关系[5]为
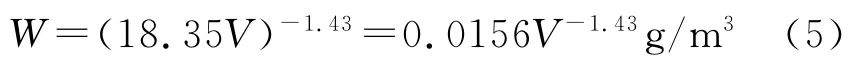
基于以上各参数之间的相互关系,将式(3)、(4)、(5)代入式(2),可以得到平流雾雾滴谱分布与能见度的关系,当雾滴半径用μm 表示时,所以得到的平流雾雾滴谱分布n(r)如下[6]
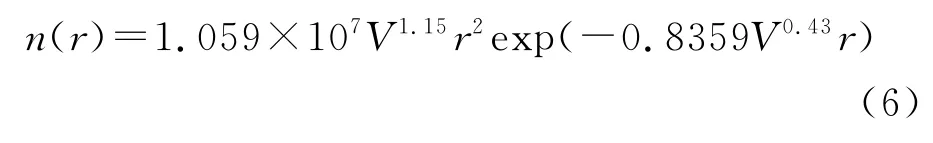
根据Mie散射理论,由雾滴谱分布及消光系数可以得出衰减系数γ为[7]

其中水的复折射指数通过双Debye 模型公式[8]计算得出。
平流雾的模式半径r0与能见度的经验关系为[9]
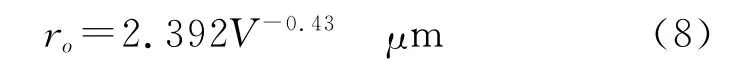
3 与其他经验衰减模型的比较与分析
激光雾中传输时,其衰减与温度、液态水含量及能见度等因素有很大关系。由于能见度测量较为容易,基于能见度的经验模型在工程中应用广泛。通常雾的衰减预测模型有ITU-R 模型[10]、Naboulsi模型[11]、Kreid模型[4]等。
1)ITU-R 模型
ITU-R 计算激光雾中衰减系数模型为

其中:Kl为比衰减系数。

式中f为频率(GHz),以及η=为水的复介电常数的实部和虚部,通过双Debye模型公式计算得出。
2)Naboulsi模型
Naboulsi模型的平流雾激光衰减系数为
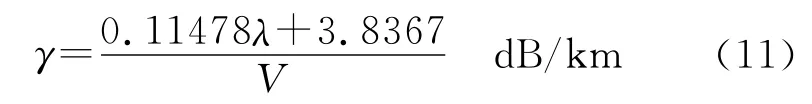
3)Kreid模型
Kreid模型指出雾的衰减系数与能见度的关系可用简单公式表示:

A为经验常数,波长λ=0.63μm 时,A=3.18,λ=10.6μm 时,A=2.1。
下面分别以常用的0.63μm 和10.6μm 波长为例,当温度为5℃,能见度为1km 时,对Mie散射模型、ITU-R 模型、Naboulsi模型和Kreid模型进行仿真分析。从图1中可以看出,各模型仿真结果总体衰减趋势相同,在重雾(能见度小于50m)情况下,各模型仿真曲线虽然有不同,但都高于200dB/km,考虑实际情况可认为没有差别;在浓雾、大雾情况下,各模型衰减系数差别较明显,均是Mie散射模型衰减系数最大,ITU-R 模型最小;当能见度大于0.5km 时各模型衰减系数差别较小,各曲线几乎重合。在计算中,经验公式仅仅反映了激光传输雾中衰减随能见度和波长变化的关系,ITU-R模型考虑了激光传输环境温度、波长和能见度等因素,而Mie散射模型不仅综合了上述各因素,同时还重点考虑了雾滴粒子尺度分布。这些因素都直接或间接地影响衰减计算的准确度,因此,相比而言Mie散射模型物理机理和概念清晰,能够全面反映传输环境物理特性对模型的影响,因而在分析计算激光雾中传输衰减特性更合理、更可靠。
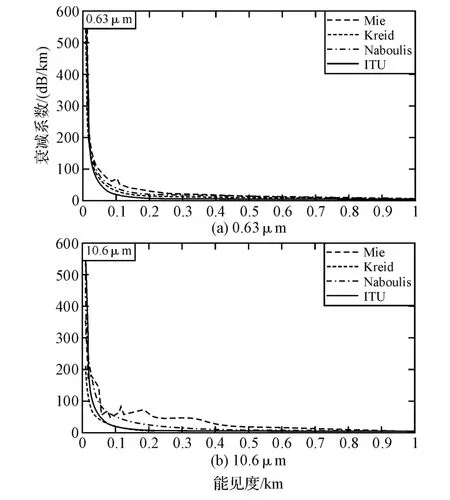
图1 0.63μm 和10.6μm 激光各模型衰减系数随能见度的变化曲线
4 激光雾中传输衰减
Mie散射模型考虑了激光与传输环境的相互作用,充分反映了海雾的物理特性对激光衰减特性的影响,提高了传输衰减的计算精度。下面通过仿真衰减系数随波长、能见度及温度的变化关系,分析三者对激光衰减的影响。
图2反映了平流雾中温度为5℃,能见度分别为0.2km、0.5km、1km 和3km 时衰减系数随波长的变化关系。从图中可以看出激光衰减并不是波长的单调函数,衰减系数随波长的变化是振荡的,在可见光波段(380nm~780nm)振荡幅度较小,在红外波段振荡幅度较大。雾滴对不同频段激光的吸收和散射效应强弱有别,而衰减系数的大小是雾滴对激光吸收和散射作用的综合体现,因此海雾对各频段激光的衰减特征是振荡变化的。随着波长的继续增大,尺度参数越来越小,散射进入瑞利散射近似区,衰减与波长成反比。
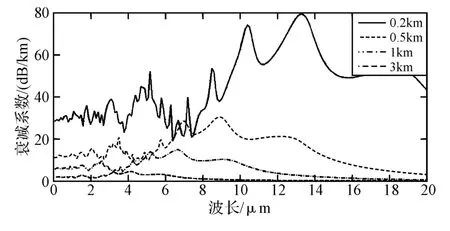
图2 衰减系数与波长变化曲线
图3反映了平流雾中温度为5℃,入射波长分别为0.63μm、1.06μm、1.55μm 和10.6μm 时衰减系数随能见度的变化关系。从上文可知,能见度与含水量关系密切,二者成反比关系,能见度越低则含水量越大,对激光造成的衰减就越强烈。从图中可以看出能见度对激光传输的影响是非常显著的,当能见度大于1km 时轻雾或者霭对激光的衰减作用不明显,但当海雾发生时,其对激光的衰减作用显著增强,尤其是当能见度低于0.3km 时,衰减系数迅速增大,在重雾情况下衰减系数更是达到200dB/km 以上,此时激光设备基本不能有效工作。

图3 衰减系数与能见度变化曲线
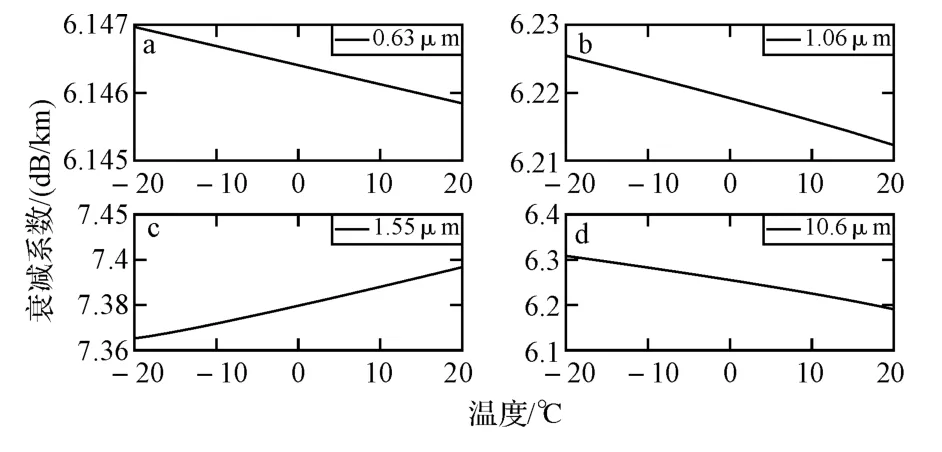
图4 不同波长条件下衰减系数随温度变化曲线
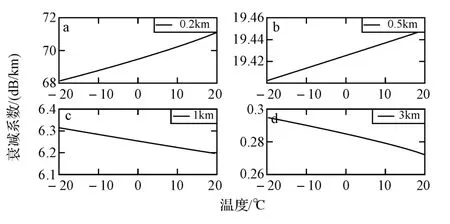
图5 不同能见度条件下衰减系数随温度变化曲线
图4~图5分别反映了平流雾中不同激光波长和能见度时衰减系数随温度的变化关系。衰减计算中,温度是在计算雾滴的复折射率时引入的,而衰减特性与海雾的复折射率密切相关。从图中可以看出,不同波长或能见度条件下温度变化对衰减系数的影响是不一样的,并且相比波长和能见度,温度变化对衰减系数的影响比较小。通过研究发现,波长一定时,衰减系数在能见度小于0.9km 时随温度的升高而增大,能见度大于0.9km 时随温度的升高而减小。而当能见度一定时,衰减系数随温度的变化在一些波段成正比,有些波段则成反比,这是由于水的介电常数受温度的影响变化对不同波段的散射与吸收不同所致。但在实际海雾天气过程中,近海面层温度变化非常有限,因此温度对激光传输衰减特性的影响不大。
5 误差来源分析
Mie衰减模型计算的精度主要依赖于对传输环境物理特性的评估,从模型中的相关参数可以看出,在分析激光雾中传输特性时,能见度、雾滴半径及雾滴谱分布是否与实际相符直接或间接地影响着衰减计算的精确性、可靠性。下面对模型中的主要误差来源进行分析。
1)雾滴谱分布
由于很难测量海雾的粒径分布和粒子密度,当前有关激光雾中传输衰减研究中雾滴谱分布通常采用经典雾滴谱如指数谱分布(如Khragian-Mazin分布模型)、幂指数率分布(如Junge谱)和对数正分布等,或者根据一定的实测数据结合各分布进行拟合[12],如此得出的雾滴谱在一定程度下可以代表某区域的雾滴谱分布,但与实际雾环境还是有相当大的差别。
2)衰减截面
本文在计算单个雾滴衰减截面时对雾滴粒径的处理上采用模式半径,由于模式半径是能见度的幂指数函数,因此当能见度一定时雾滴的衰减截面也是确定的,而不同半径雾滴的衰减截面是不同的,因此相比根据雾滴谱分布中各变化半径得出的衰减结果有一定的误差。
3)能见度
能见度的测量主要有传统人眼观测、利用观测仪器进行测量等。前者由于受观测者主观因素的影响而产生较大的观测误差,后者由于观测原理等原因使得其测量精度难以保证。在本文衰减计算中,能见度不仅对模式半径有影响,也是雾滴谱分布中的关键参数,因此能见度测量的中的误差将对计算结果产生较大影响。
随着海雾数值模式的发展与完善,利用气象数值预报模式对海雾的激光传输特性进行分析已成为可能。利用WRF、MM5 或RAMS等海雾数值模式可以得出实时海雾特征参量,再通过Fortran和Matlab编程工具将模式输出数据与Mie散射模型进行连接,进而可提高模型计算的精确性和有效性,这也是下一步需要继续研究的内容。
6 结语
本文基于Mie理论建立了激光雾中传输衰减模型:
1)通过与其他经验模型的比较分析,说明了Mie衰减模型更可靠、有效。
2)仿真了衰减系数随波长、能见度及温度的变化,通过分析发现,衰减系数随着波长变大而振荡变化;能见度对衰减系数的影响最大,二者成反比关系;相对波长、能见度,温度对衰减特性的影响相对较小。
3)总结分析了雾滴谱分布、衰减截面、能见度三者的误差对Mie衰减模型计算的影响,提出一种提高模型计算精度的方法,并分析了其可行性。
[1]王彬华.海雾[M].北京:海洋出版社,1983:1-5.
[2]盛裴轩,毛节泰,李建国,等.大气物理学[M].北京:北京大学出版社,2003:301-303.
[3]周星里,谢亚楠,杨正得.雨雾对电磁传输特性影响的研究[J].气象科技,2011,39(5):661-665.
[4]ZHAO Zhen-Wei,WU Zhen-Sen.Millimeter-wave attenuation due to fog and clouds.Conference Digest[C]//25th International Conference on Infrared Millimeter Waves,Beijing,2000:469-470.
[5]Ippolito L J.Propagation effects handbook for satellite system design[J].NASA Reference Publication,1989,1082(4):6-71.
[6]柯熙政,马冬冬,刘佳妮.激光在雾中传输的衰减研究[J].光散射学报,2009,21(2):104-109.
[7]李娣,陈辉.激光大气传输的雨雾衰减特性研究[J].电子设计工程,2011,19(9):1-5.
[8]肖璐.Ka频段雨衰减特性的测量和模型研究[D].西安:西安电子科技大学,2010.
[9]孙超,王红霞,傅关新,等.雾对激光的衰减特性研究[J].光散射学报,2011(3):201-205.
[10]REC.ITU-R P.840-4:Attenuation due to clouds and fog[S].2009,10:1-3.
[11]Nadeem F,Flecker B,Leitgeb E,et al.Comparing the fog effects on hybrid network using optical wireless and GHz links[C]//Networks and Digital Signal Processing,2008:278-282.
[12]李学彬,宫纯文,李超,等.雾滴谱分布和雾对红外的衰减[J].激光与红外,2009,39(7):742-745.

