基于混合优化算法的曲线曲面优化设计方法研究

2014-11-22 02:12:12王毛毛赵卫国冯盈雪

机械工程师 2014年1期

王毛毛，赵卫国，冯盈雪

（内蒙古工业大学机械学院机械工程系，呼和浩特 010051）

0 引言

随着社会的进步，科学技术的不断发展，人们对产品的外形有了多方面的要求，对产品曲面精度要求也越来越高，因此曲线曲面的光顺要求就成了曲面造型设计的重要部分，如何评判曲线曲面是否光顺以及怎样使曲线曲面更加光顺就成了曲线曲面造型的核心问题。能量法是曲线曲面光顺常用的一种整体优化法，它是把光顺问题转化为最优化问题而进行求解的。遗传算法是通过生物自然选择中的选择、遗传、变异等自然机制来提高各个个体的适应性，从而选择出更能适应生存的个体。遗传算法的最好优点就是能与其他算法进行结合，对其它算法的兼容性比较好。所以提出遗传算法结合蚁群算法，形成一种新的曲线曲面光顺方法，该方法结合改进的网格能量法，能够得到更好的曲线曲面光顺效果。

1 曲线光顺优化能量法

1.1 能量法的基本原理

根据能量法原理，把通过所有数据型值点Pi（i=0，1，…，n）连接而成的三次均匀B 样条曲线设定为P0（t），而P（t）是光顺后的三次均匀B 样条曲线，数学分析中P（t）是过型值点Qi（i=0，1，…，n）连成曲线的样条函数，则曲线P（t）的应变能为：

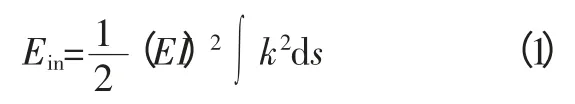
式中，常数EI 表示样条的刚度系数，k 表示曲率。在曲线曲面光顺性的曲率分析中，若希望曲线曲面更光顺，只需使三次均匀B 样条曲线的应变能更小即可。根据此原理，建立一个模型，就是把光顺前后的型值点Pi与Qi之间挂上一条小弹簧，弹簧的弹性系数为βi，由于光顺前后的型值点都有偏移，所以每个小弹簧上都有能量，所有小弹簧总的能量为：

小弹簧的能量模型已经建立，这样就能得到优化的模型（即样条和小弹簧在内的整个系统总能量），总能量的表达式为：

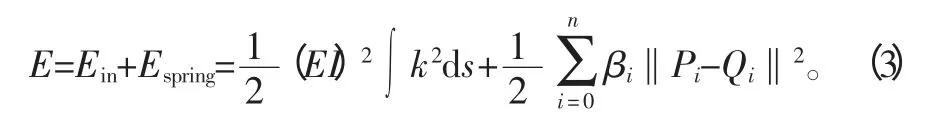
式中：（EI）2＝α，曲线P（t）光顺的目的就是使曲线的总能量E 达到极小值；Ein的大小表示曲线光顺的情况；Espring反映了光顺后的曲线逼近原始曲线的情况。对于曲线P（t）光顺程度要求越高，则曲线光顺的应变能Ein就得越小，对于要求光顺后的曲线越是逼近光顺前的原始曲线，则小弹簧的总能量Espring越小［1］。至此，这样就能把实物模型的曲线光顺的问题转换成数学模型进行优化的问题。

1.2 能量法光顺的基本公式

设曲线P0（t）和P（t）分别为光顺前后的三次B 样条曲线，其表达式分别为：

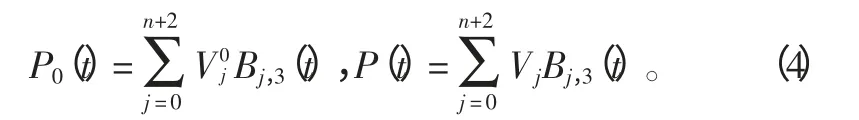
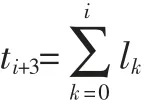
将式（3）代入Vi-Vt=λ（Vt-Vj）中得到：

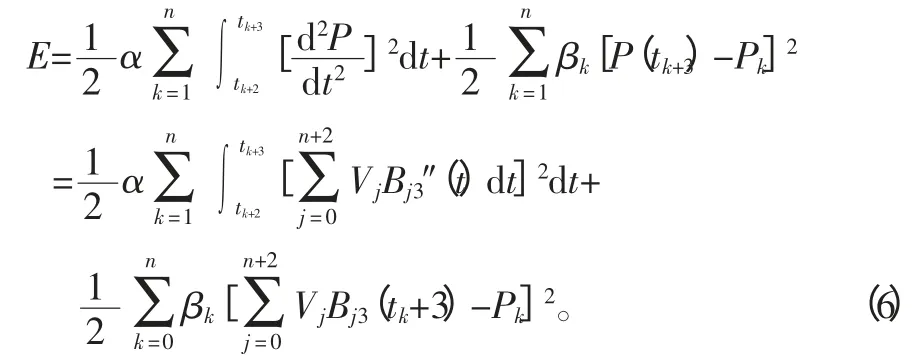
为使E=min，令∂E/∂Vt=0 得到

式（4）是关于｛Vi｝（i=0，1，…，n+2）建立的方程组。记V=（V0，V1，…，Vn+2）T则可以改将式（7）写成如下矩阵形式：

式中，A＝（αij）n+3，n+3是根据α 建立的系数矩阵，其元素表达式为：

C＝（C0，C1，…，Cn+2）为式（7）右端向量，其分量为:

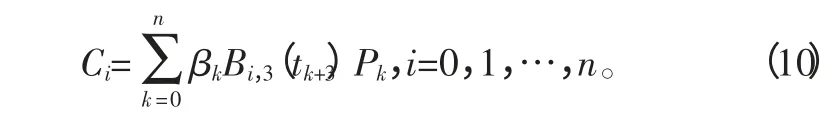
当｜i-j｜＞3 时，αij=0 是线性方程组的系数矩阵，利用高等数学方法求解线性方程组，求得的有化解就是曲线的控制顶点Vi（j=0，1，…，n+2），代入式（2）就能得到光顺后的曲线P（t）。

1.3 改进的曲线能量法

根据实际情况，为了在用能量法对目标函数进行光顺处理时，得到符合要求的后背曲线曲面，提出了两种约束方法，即对控制点和型值点的约束。最终设定人体后背脊柱曲线的目标函数及约束条件如下：

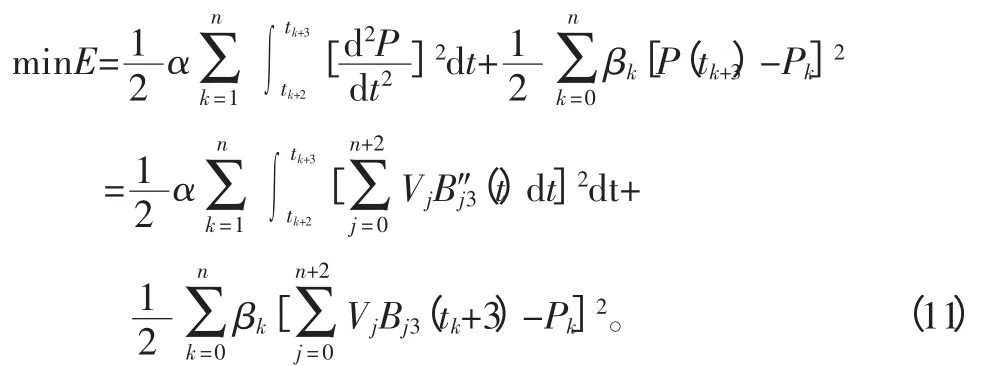
约束条件：

2 基于遗传蚁群算法的曲线优化

2.1 遗传蚁群算法的基本思想

遗传蚁群算法GAACA 的原理就是吸取遗传算法和蚁群算法的精华，去掉遗传算法和蚁群算法糟粕，就是分别吸取各自的优点，去掉不足，使两种方法更好地结合。遗传算法相比蚁群算法优点是计算速度快，精度不足，而蚁群算法相比遗传算法就是精度准确，计算速率比较缓慢。遗传蚁群算法继承了两种算法的优点，就是计算速度快，计算精度高［5］。为了提高速度与精度，把遗传蚁群算法主要分成两部分，上半部分是应用遗传算法计算，这是利用遗传算法计算速度快，全局收敛结构高的特点，在数据全局收敛速度急速下降也就是快达到最优解的时候，遗传算法的计算速率同时下降的比较快，这时候的解保存起来在后面应用。下半部分是应用蚁群算法，因为这时候已经有需要下一步计算的数据基础，在这个基础上再应用蚁群算法，就能较好地体现出蚁群算法的并行性和计算速率快的特点。这样就能应用两种优化算法的各自优点来提高数据优化的精度和速率。

2.2 遗传蚁群算法的过程

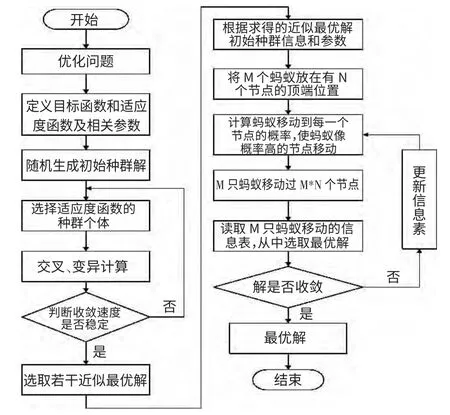
图1 遗传蚁群算法过程

2.3 遗传蚁群算法在曲线曲面优化中的应用

应用遗传蚁群算法，上半部分是遗传算法的设定，其中设置种群的大小为NIND=50，交叉概率PC=0.2，变异概率PM=0.01，变量的二进制位数PRECI=30，代沟GGAP=0.9，设定计算精度保留到小数点后4 位，设定种群在迭代计算时，迭代满5 代就任意抽出3 个最佳个体，判断这些个体收敛是否停滞，若停滞便停止遗传算法的运算，选出其中10 个近似最优解的数据作为下半部分蚁群算法的初始数据，在进行蚁群算法时，设定参数蚂蚁的种群为30，α=1，β=4，ρ=0.8，运行的最大次数NC=20，整个遗传蚁群算法运算6 次，其结果就比较令人满意。

3 曲线优化实例验证

在此过程中，取通过三坐标测量仪测出的一部分脊柱曲线数据点作为优化前脊柱曲线数据，并把已知型值点转化为曲线控制点，通过对控制点的约束来改进网格能量法，最后用遗传蚁群算法进行优化计算。

首先通过利用MATLAB 软件对测量数据点进行拟合，通过得到的脊柱数据拟合曲线如图2 所示。

利用改进网格能量法就可以得到光顺后的曲线，如图3 所示。

利用遗传算法、蚁群算法及遗传蚁群算法优化后的曲线及其精度如图4 所示。

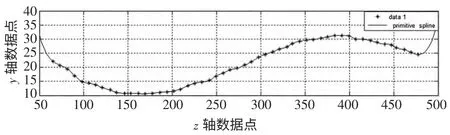
图2 初始数据点拟合曲线图

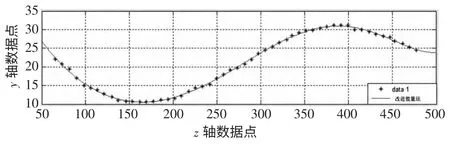
图3 能量法曲线光顺图

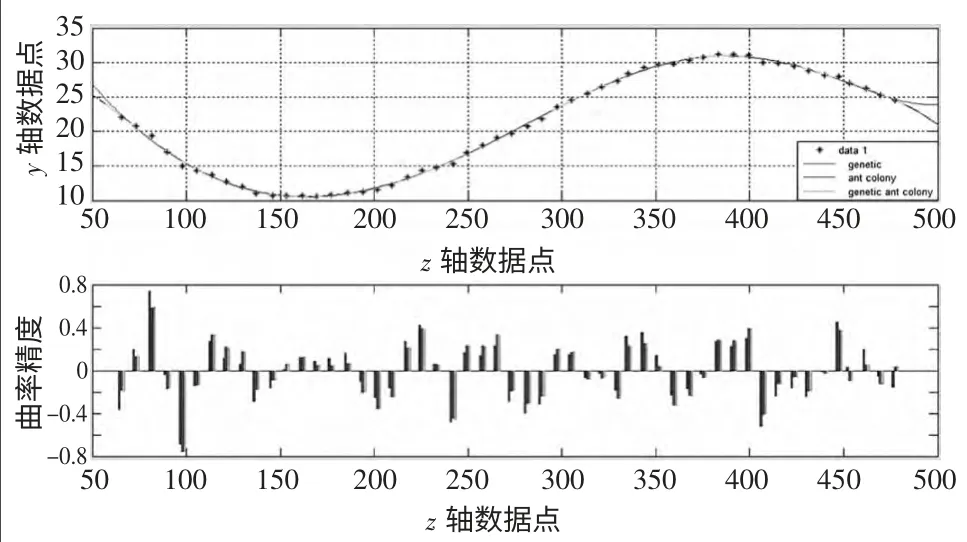
图4 各算法优化曲线及精度比较图

曲线优化结果：由图2～图4 可以看出，利用改进网格能量法以及控制点约束条件建立数学模型，并用遗传蚁群算法进行计算得出的曲线精度更高，同时曲线的收敛性也是三种算法中最快的，以此证明了此方法的有效性。所以用蚁群算法同样对后背其它曲线进行光顺，在此基础上完成后续曲面优化。

4 曲面能量法优化数学模型及其实例验证

4.1 曲面能量法优化数学模型

曲面网格能量法是一个是带有约束的最优化问题，它的精确求解计算量非常大。因此，为将其简化，我们引进罚因子，将其近似地转化成一个无约束问题再进行求解，该目标函数就成为

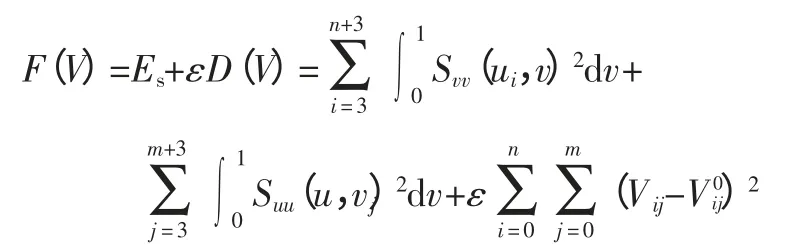
求解线性方程组，使F（V）达到极小，就得到了光顺后的曲面S（u，v）的控制顶点。

4.2 优化结果

在应用遗传蚁群算法及能量法进行曲面优化过程中，与曲线优化一样，首先将以上得到的曲面型值点反求，从而得到优化前曲面的控制顶点，利用网格能量法建立数学模型，再通过遗传蚁群算法进行优化运算，从而得到优化后曲面新的控制顶点，完成曲面优化运算，虽然利用这种算法进行的曲面优化更光顺，曲率变化更均匀，但是，应用此方法的计算量很大，计算过程过度繁琐。所以，曲面优化要借助于曲线优化方法，从而使过程更加简单，为此提出先把脊柱曲线和几条横向背部曲线进行优化(横向曲线优化方法如脊柱曲线)，用优化后的曲线形成曲面，最后用曲率分析验证优化结果。优化前曲线如图5，优化后曲线如图6 所示。