亚临界区雷诺数下圆柱绕流场电磁力控制数值研究

尹纪富，尤云祥，李 巍

(上海交通大学 海洋工程国家重点实验室，上海 200240)

在海洋工程中，圆柱型结构有广泛的应用，其中包括海洋输油气管道、钻探与生产立管和浮式平台的立柱等。这类圆柱型结构在海流作用下会产生所谓的涡激振动现象，并导致其疲劳损伤等问题。因此，如何抑制圆柱型结构绕流产生的周期性涡脱落现象问题，一直是海洋工程中的热点之一［1］。目前，对圆柱型结构绕流场控制的方法主要有被动和主动式两类控制方法［2］。被动控制需要在圆柱体表面附加额外的装置，如隔离板和肋条等［3-4］，而主动控制则需要向流场输入能量，如表面狭缝吹吸抽气、尾流喷射和电磁力控制等［5-6］。由于电磁力是一种体积力，可直接向流场注入动量，不改变流体质量，而且无运动部件、可靠性高、易于实现和响应速度快，因此电磁力主动流动控制方法具有独特的优势［7］。

早期的研究大多集中于电磁力对平板及道槽边界层流动的影响等问题［8-9］。在最近二十多年中，采用实验等方法，对电磁力控制圆柱层流绕流场特性问题的研究表明，电磁力可以抑制圆柱绕流场的流动分离，改变绕流场中脱落涡结构，减小圆柱体阻力等［10-16］。研究进一步表明，对高雷诺数下电磁力也能显著改变圆柱绕流场特性，减小其阻力［17-18］。对实际海洋工程中的圆柱型结构，其雷诺数一般至少为103量级，在这种高雷诺数下圆柱型结构的绕流场将具有明显的三维随机特性。然而，对高雷诺数下电磁力控制圆柱型结构绕流场及其升阻力机理等问题，迄今尚不十分清楚。

实验室实验是目前研究电磁力对圆柱绕流场影响问题的主要手段之一，由于实验条件的限制，因此目前文献中所考虑的雷诺数一般都在103量级以内。随着高性能计算机及现代计算流体力学理论的发展，采用CFD(computational fluid dynamics)方法研究高雷诺数圆柱绕流场特性问题已成为当今的主要手段之一，包括直接模拟(DNS)、雷诺平均模拟(RANS)、大涡模拟(LES)和脱体涡模拟(DES)等［19-23］。其中，DNS 和LES方法计算量太大，在当前计算机条件下还只限于低雷诺数湍流的数值模拟。在高雷诺数下，由于附面层和大范围流动分离等是圆柱绕流场中的典型流动现象，而受到现今湍流模式的限制，RANS 方法的数值模拟结果不尽人意。DES 是一种介于LES 和RANS 之间的方法，它既能模拟非定常大范围分离流动，又具有计算量少的特点，因此已成为钝体绕流数值模拟的主要手段之一。

有鉴于此，利用Maxwell 方程直接数值计算表面包覆电磁极圆柱体产生的三维电磁力，将其加入到流场控制方程中。在此基础上，针对两个亚临界雷诺数Re = 3.9 ×103和Re = 5.0 ×104，采用基于SST k-ω 湍流模式的DES 方法，数值模拟与分析电磁力对圆柱体三维绕流场结构及其升阻力特性的影响机理与规律。

1 数值模拟方法

在圆柱体表面覆盖相间分布的电极和磁极，将其置于弱电解质中，当电极通电后在弱电解质中形成电场并与永磁体产生的磁场相互作用，产生流向的电磁力，如图1 所示。其中，磁极为永磁体，磁场大小和方向都不随时间变化。电极为导电体，通过施加恒定的电压产生电场，电场大小和方向不随时间变化。当弱电解质流体流经包覆电极与磁极的圆柱体时，流体受到电磁力的作用，从而改变圆柱体的绕流场特性。

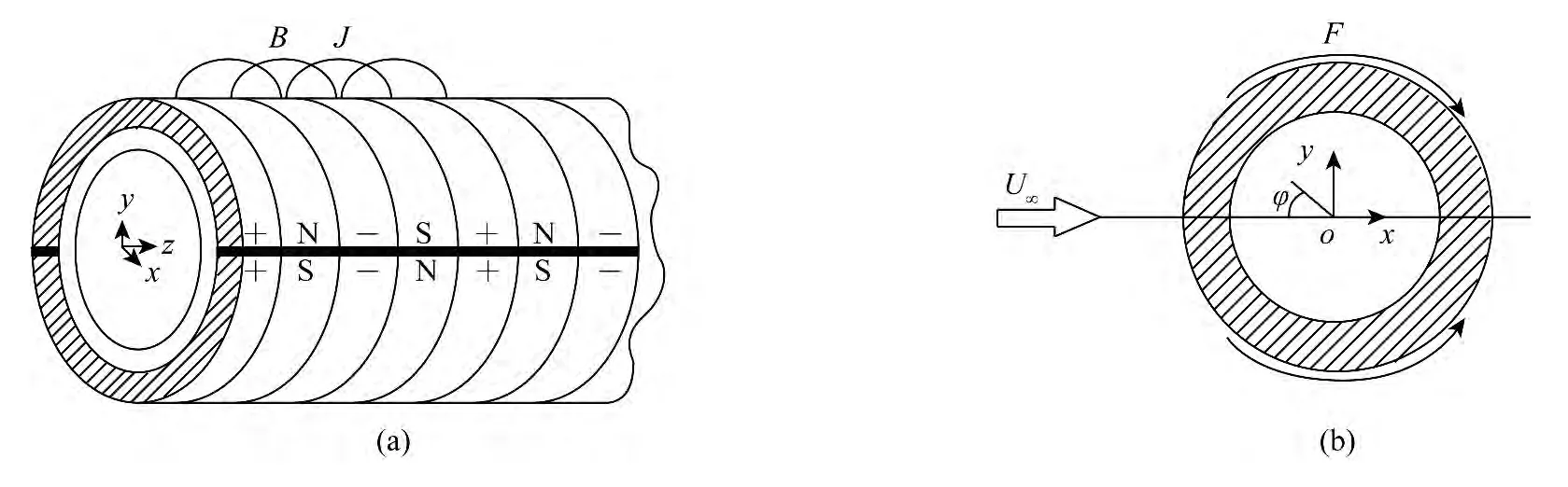
图1 表面覆盖电极与磁极的圆柱体模型及其坐标系Fig.1 The model of the circular cylinder covering the electromagnetic actuators and its coordinate system

将电磁力作为体积力加入到动量方程中，可得不可压弱电介质的Navier-Stokes 方程为

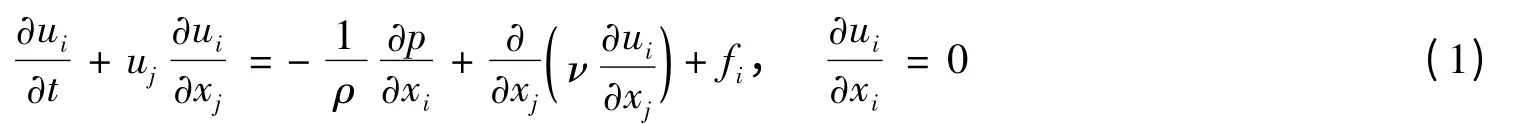
式中:t 为时间，ρ 为电介质密度，υ 是电介质动力黏性系数，u=(u1，u2，u3)为速度矢量，(x1，x2，x3)为空间坐标，p 为扰动压力，F = (f1，f2，f3)为Lorentz 力。

流动的弱电解质在电磁场中受Lorentz 力的作用可表示

式中:J 为电流密度矢量，B 为磁感应强度矢量，E 为电场强度矢量，σ 为弱电解质电导率。由于海水作为弱电解质，其感生电流很小，感生电流产生的作用力可以忽略，故式(2)可简化为式(3)。

采用DES 方法对控制方程(1)进行数值模拟，这是一种在附面层内采用RANS 方法，而在附面层外的区域采用LES 方法对圆柱绕流场进行数值模拟的方法。为此，对圆柱体附面层内的区域，以RANS 方程为控制方程，采用SST k-ω 湍流模式封闭模型;在圆柱体附面层外的区域，把湍流瞬时运动通过空间滤波方法分解为大尺度和小尺度运动两部分，前者通过直接求解空间滤波方程计算，后者则概化为亚格子雷诺应力，并采用Smagorinsky 亚格子模型进行求解。

在SST k-ω 湍流模式中，k 方程耗散项中的湍流尺度参数lk-ω可表示为

式中:βk为模型常数，取值为βk= 0.09 。

在DES 方法中，定义RANS 和LES 的分辨尺度lDES为

为了防止过早地开启亚格子应力模型，引起附面层内雷诺应力的急剧下降，导致非物理性质的分离，并产生网格诱导分离现象，将式(5)中的系数CDES取为0.61，而网格尺度Δ 取为

其中，Δx1，Δx2和Δx3分别为三个坐标轴方向的网格尺度。

在紧贴物面的区域，由于lk-ω≤CDESΔ，因此lDES= lk-ω，这时在DES 中的湍流模型即为RANS 中的SST k-ω 湍流模式。在其它区域，由于lk-ω＞CDESΔ，因此SST k-ω 湍流模式生成和消散源项中的lk-ω被替换为CDESΔ，当生成与消散作用达到平衡时，SST k-ω 湍流模式中的湍动粘度与Smagorinsky 亚格子模型中的亚格子涡粘系数形式相似，这时DES 即起到类似LES 的作用。

利用Maxwell 方程，采用有限元方法，对表面包覆电极与磁极圆柱体产生的三维电磁力分布进行数值计算。永磁铁磁场强度取为0.35 特斯拉，电极与磁极宽度均为0.1D，其中D 为圆柱体直径。设n 为圆柱体表面任意展向断面点P(D/2，φ)处的法向矢量，r 为法线n 上的点到圆柱表面的距离，无量纲半径为=r/D。

在图2 中，给出了圆柱体表面电磁力沿法向和展向分布的数值结果。其中，图2(a)为当φ = π/2 时电磁力沿法向分布的数值结果，图2(b)为某个展向截面上电磁力分布的等势线结果。电磁力分布在法向上呈现指数衰减特征，在圆柱体展向呈现周期性变化特征［16］。

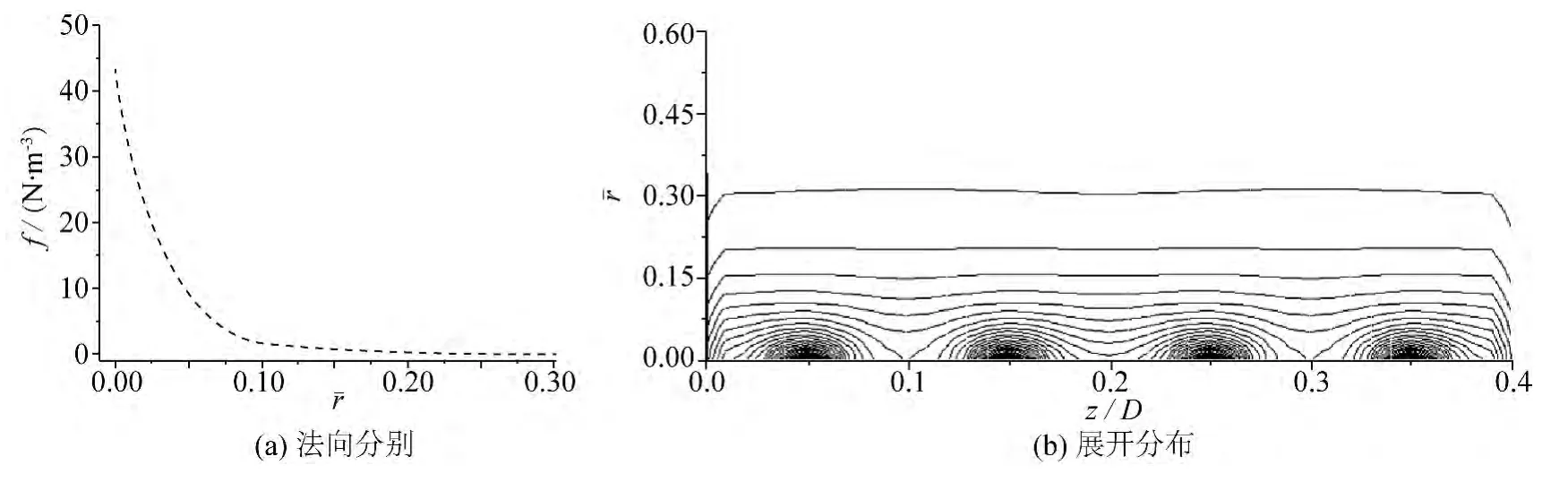
图2 圆柱体表面电磁力沿法向和展向分布的数值结果Fig.2 Numerical results for normal and spanwise distributions of the electromagnetic force on the circular cylinder surface

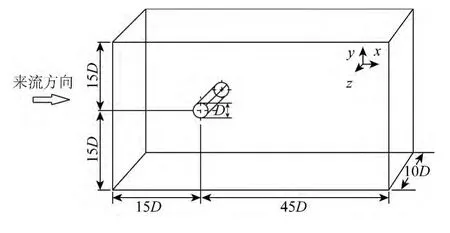
图3 计算区域示意Fig.3 The sketch of the computational domain

数值模拟中，流场控制区域如图3 所示，弱电解质流体密度为ρ = 1 025 kg/m3，电导率为σ = 5 s/m，动力学粘性系数为ν = 10－6m2/s。以圆柱体中心轴线为基准，来流上游为15D，下游为45D，中心轴线距离上下边界均为15D，圆柱体展向长度为10D;入口边界选为速度入口，出口边界为自由出流条件，上下边界为壁面边界条件，圆柱表面为无滑移边界条件，计算初始条件为给定进口速度边界条件。

分别采用O 型网和H 型组合网格对流场控制区域进行网格划分，网格全部为六面体结构网格。在靠近圆柱壁面处对网格进行局部加密，为了让圆柱体壁面处的第一层网格满足y+≈1 ，用y+= 0.172Δy Re0.9/D估算Δy，确定第一层网格控制点离开壁面的距离Δy，并沿径向网格逐步放大。采用有限体积法离散动量和连续性方程，对流项采用三阶精度QUICK(quadratic upstream interpolation for convective kinetics)格式，扩散项采用二阶中心差分格式，压力速度耦合迭代采用SIMPLE(semi-implicit pressure linked equation)算法。

2 结果与分析

定义雷诺数和电磁力作用参数为

式中:u∞为来流速度，j0= σE0为平均电流强度，E0为平均电场强度，B0为平均磁场强度。

定义圆柱体总阻力系数Cd和总升力系数Cl为

式中:Fd为圆柱体总阻力，Fl为圆柱体总升力，S 为圆柱体迎流面面积。

在数值模拟中，雷诺数为Re = 3.9 ×103和Re = 5.0 ×104，网格总数分别为1.6 ×106和2.1 ×106。数值模拟的初始时间步长在Re = 3.9 ×103时为Δt = 0.05 s，在Re = 5.0 ×104时为Δt = 0.005 s。首先对没有电磁力作用时圆柱绕流场特性进行数值模拟，定义无量纲时间为= tU/D。结果表明，当无量纲时间=315 时，圆柱绕流场已经达到稳定状态。然后，再对圆柱体施加电磁力作用直到= 375 ，此时在电磁力作用下圆柱绕流场也已经达到稳定状态。

两个雷诺数Re = 3.9 ×103和Re = 5.0 ×104均属于亚临界区范围内，此时圆柱绕流场中边界层仍为层流分离，但尾流场流动已经转变为完全湍流状态，如图4 所示，图中Ωz为三维涡量场。结果表明，对两个亚临界雷诺数，在圆柱绕流场中，不仅有流向漩涡的卷起和脱落，而且在展向也有大尺度的脉动存在;在漩涡向下游发展的过程中，由于展向发尺度脉动的存在，涡街产生明显的扭曲现象;在圆柱体展向不同断面处的涡街脱落形式、相位及涡脱落强度均不尽相同，圆柱绕流场存在明显的三维特性。随着雷诺数的增大，在圆柱绕流场中心区域涡的尺度变大，在其外层的小尺度湍流涡愈为明显，并且其垂向及下游发展范围增大。

图4 当 = 315 时圆柱绕流场涡量分布的数值结果Fig. 4 Numerical results for the vorticity distribution of the flow around a circular cylinder when = 315

图5 给出了两个雷诺数下圆柱体总阻力和总升力系数时历特性的数值结果。由图可知，在两个雷诺数下，圆柱体总阻力和总升力系数均出现随机脉动现象，但仍具有准周期特性，这表明圆柱绕流场中的涡脱落不仅具有准周期性，而且存在随机脉动性;随着雷诺数增大，总阻力和升力系数随机脉动幅值随着变大。

设f 为涡泄频率，定义St = fD/u∞为Strouhal 数，记为平均总阻力系数，Clrms为总升力系数的均方差，而为平均分离角。在表1 中，给出了两个雷诺数下St、、Clrms和计算与文献结果的比较。其中，文献［24］采用的是经验公式，文献［19］采用的是DES 数值计算方法。由表可知，本计算与文献结果一致，因此这里的计算结果是合理和可靠的。

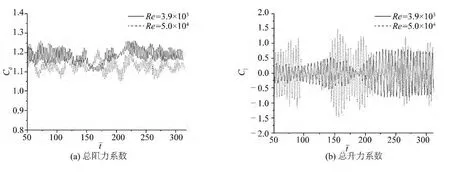
图5 圆柱体总阻力系数和总升力系数的数值结果Fig. 5 Numerical results for total drag/lift coefficients of the circular cylinder

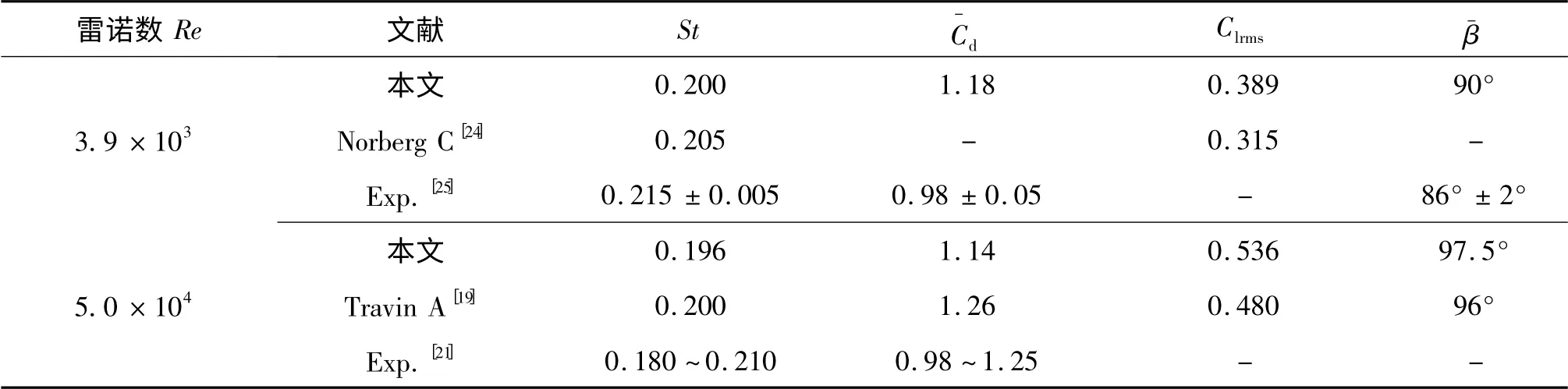
表1 本文与文献结果的比较Tab.1 Comparisons of the present results with the reference ones

2.1 电磁力对圆柱绕流场特性的影响

在图6 中，给出了在五个不同电磁力作用参数下圆柱绕流场涡量分布的数值结果。由图可知，电磁力的作用首先改变圆柱体近壁面处的涡量场特性使得涡量场沿圆柱体展向的变化减弱;随着电磁力作用参数的增加，开始影响其绕流场中下游的涡量场特性;当电磁力作用参数超过某一临界值后，在圆柱体尾部产生射流现象。

在两个不同亚临界区雷诺数下，电磁力对圆柱绕流场涡量分布的影响规律如下:

当N = 0.5 时，对Re = 3.9 ×103，电磁力对圆柱绕流场涡量分布有一定的影响，但并不明显;对Re =5.0 ×104，在电磁力作用下，圆柱绕流场中心区域涡的尺度变小，在其外层的小尺度湍流涡减弱，而且垂向发展范围变小。当N =1.0 时，对Re =3.9 ×103，在圆柱体展向的大尺度脉动现象减弱，准周期脱落涡转变为周期性的脱落涡;对Re = 5.0 ×104，在圆柱体展向的大尺度脉动已基本被抑制，绕流场中心区域涡的尺度进一步变小，在其外层的小尺度湍流涡进一步减弱，而且垂向发展范围也进一步变小。当N = 2.0 时，对Re = 3.9 ×103，圆柱体尾部流动分离已基本被抑制，尾流场中的漩涡已经转变为尺度很小的漩涡结构，而且已不存在明显的周期性特征;对Re = 5.0 × 104，圆柱体尾部流动分离已被抑制，尾流场中已不存在大尺度涡现象，在电磁力作用下开始形成射流现象。当N = 4.0 和6.0 时，对Re = 3.9 ×103，圆柱体尾部流动分离已被抑制，在电磁力作用下形成射流状态;对Re = 5.0 ×104，圆柱体尾部射流现象愈为明显，尾流场与层流流动现象类似。

下面给出电磁力对圆柱绕流场流动分离的影响，结果如图7 所示。由表1 可知，当没有电磁力作用时，在Re = 3.9 ×103下的平均流动分离角度要比在Re = 5.0 ×104下的平均流动分离角小约7.5° ，而且在不同展向断面处的分离角度并不相同。由图7 可知，存在一个临界电磁力作用参数Nc1(≈1.0)，当N ＜Nc1时，对两个亚临界区雷诺数，在电磁力作用下圆柱体各展向断面处的流动分离角度是不同的，即流动在展向具有明显三维特性;当N ＞Nc1时，对两个亚临界区雷诺数，在电磁力作用下圆柱体各展向断面处的流动分离角度趋于相同，即流动在展向的三维特性随着减弱直至消失。对Re = 5.0 ×104，当N ≈2.0 时流动分离角达到130.9° ，然后在电磁力作用下流动分离角度消失。对Re = 3.9 ×103，当N ≈3.0 时流动分离角达到126° ，然后在电磁力作用下流动分离角度才消失。

图6 当 = 375 时，电磁力对圆柱绕流场涡量分布影响的数值结果Fig.6 Numerical results for the effect of the electromagnetic force on the vorticity distribution of the flow around a circular cylinder when = 375

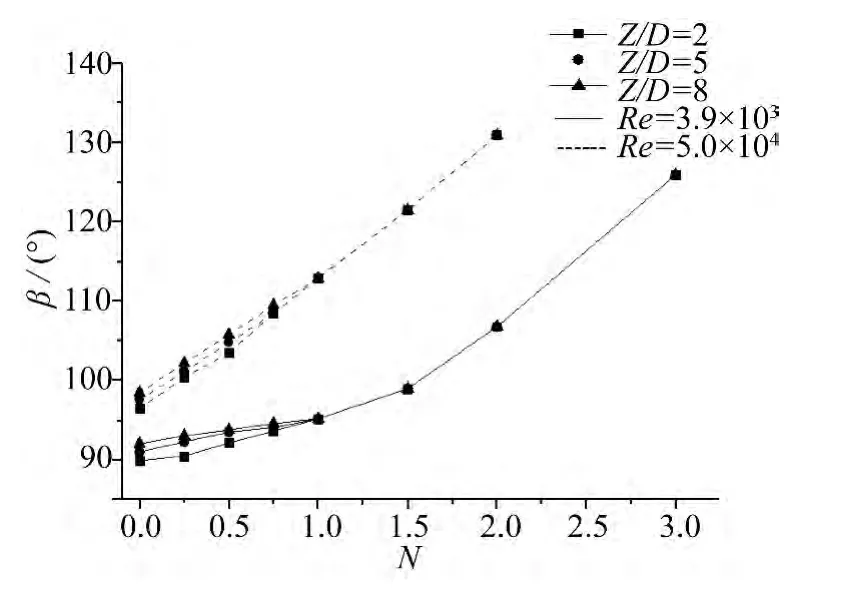
图7 在不同展向断面处流动分离角随电磁力作用参数变化特性Fig. 7 Variation characteristics of the separated angles with the electromagnetic interaction parameters at different spanwise cross-sections

在圆柱体近壁面处的切向速度大小代表了其边界层内外流体动能的大小，图8 给出了电磁力对圆柱体近壁面切向速度影响的数值结果。其中，u 为沿n 的切向速度，n 为圆柱体表面上点P(0，π/2)处的法向矢量。由图可知，电磁力可以增大圆柱体近壁面处的切向速度，即增大其边界层内外的流体动能，从而改变圆柱绕流场特性。在两个不同亚临界区雷诺数下，电磁力对圆柱体近壁面处切向速度的影响规律如下:

当没有电磁力作用时，在圆柱体不同展向断面处切向速度沿法向的变化特性及其最大值位置均不相同，即在圆柱绕流场中有明显的三维效应。当N = 0.5 时，对Re = 3.9 ×103，电磁力对圆柱体近壁面处切向速度的影响并不明显;对Re = 5.0 ×104，电磁力对圆柱体近壁面处的切向速度产生明显影响，在不同展向断面处切向速度沿法向的变化特性及其最大值位置已趋于一致。当N = 1.0 时，对两个亚临界区雷诺数，电磁力的作用使圆柱体在不同展向断面处切向速度沿法向的变化特性及其最大值位置均趋于一致，而且当Re =5.0 ×104时切向速度的最大值明显增加。

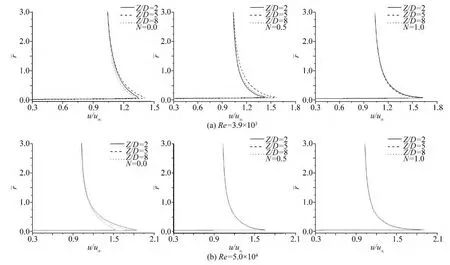
图8 当 = 375 时，电磁力对圆柱体近壁面处切向速度的影响Fig.8 The effect of the electromagnetic force on the tangential velocity near the circular cylinder wall when = 375

2.2 电磁力对圆柱体升阻力特性的影响

在图9 中，给出了电磁力对圆柱体总阻力系数影响的数值结果。由图可知，电磁力可以显著减小圆柱体平均总阻力系数及其脉动幅值。对Re = 3.9 ×103，当N = 6.0 时，圆柱体平均总阻力系数的减小幅度超过90%。对Re = 5.0 ×104，当N = 2.0 时，圆柱体平均总阻力系数的减幅接近100%，而且在N ＞2.0 后圆柱体还会受到电磁力产生的净推力作用。

图9 电磁力对圆柱体总阻力系数时历的影响Fig.9 The effect of the electromagnetic force on the time history of the total drag coefficient for the circular cylinder

在图10 中，给出了圆柱体平均总阻力系数随电磁力作用参数变化特性的数值结果。由图可知，在两个亚临界区雷诺数下，随着电磁力作用参数的增大，圆柱体平均总阻力系数均随着减小;在相同电磁力作用参数下，在Re = 5.0 ×104时圆柱体平均总阻力系数的减幅要远大于Re = 3.9 ×103的情况;对Re=3.9 ×103，圆柱体平均总阻力系数随电磁力作用参数近似呈二次曲线形式减小;对Re =5.0 ×104，圆柱体平均总阻力系数随电磁力作用参数则近似呈幂指数形式减小。

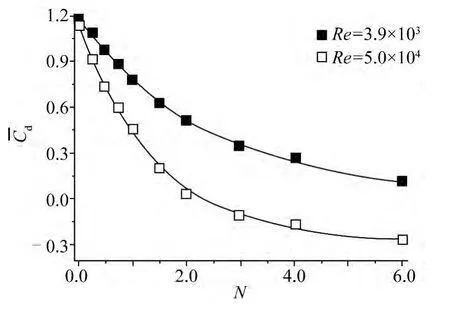
图10 圆柱体平均总阻力系数随电磁力作用参数变化特性Fig.10 Variation characteristics for the total average drag coefficient of the circular cylinder with the electromagnetic force interaction parameters

圆柱体总阻力由压差力和摩擦力两个部分组成，压差阻力主要由流体流经圆柱体时在其前后形成的压差所引起，而摩擦阻力主要由边界层内流体的粘性组成。在图11 中，给出了电磁力作用下圆柱体平均总压差力系数和平均总摩擦力系数的数值结果。结果表明，在两个亚临界区雷诺数下，平均总压差力系数随电磁力作用参数增大而减小，而平均总摩擦力系数则随电磁力作用参数增大而增大;在相同电磁力作用参数下，在Re = 5.0 ×104时圆柱体平均总压差力和摩擦力系数系数的减幅要远大于Re = 3.9 ×103的情况;对Re = 5.0 ×104，当N ＞2.0 时，由于圆柱体受到电磁力产生净推力的作用，平均总压差力为负值。

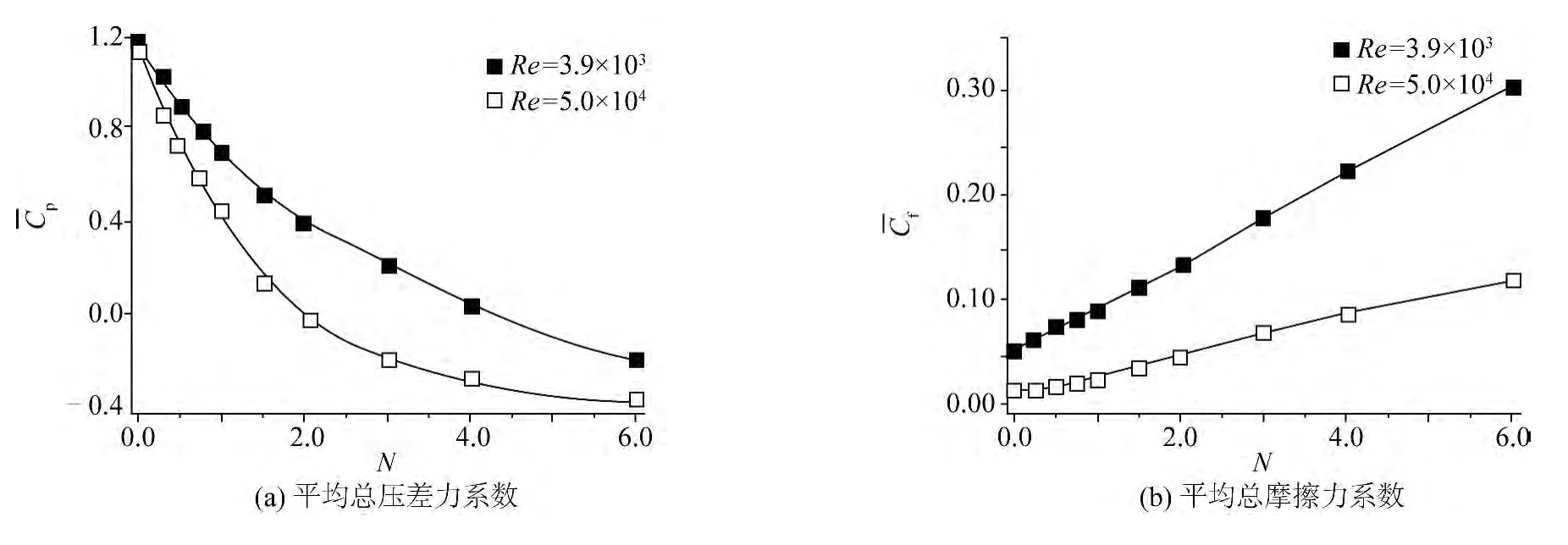
图11 圆柱体平均总压差阻力和摩擦阻力系数随电磁力作用变化特性Fig.11 Variation characteristics for the total average pressure and friction coefficients of the circular cylinder with the electromagnetic force interaction parameters

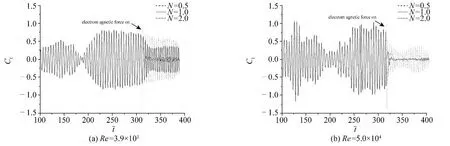
图12 电磁力对圆柱体总升力系数时历的影响Fig.12 The effect of the electromagnetic force on the time history of the total lift coefficient for the circular cylinder

在电磁力作用下，圆柱体尾涡特性将发生变化，因此其升力系数也将发生变化，结果如图12 所示。由图可知，电磁力作用可以减小圆柱体总升力系数的脉动幅值，而且当电磁力作用参数达到某个值后，总升力系数的脉动幅值接近为零。当N =0.5 时，对Re =3.9 ×103，由于电磁力对圆柱体尾涡的影响较小，因此总升力系数脉动幅值的减小幅度并不明显;对Re =5.0 ×104，总升力系数脉动幅值明显减小。当N = 1.0 时，对Re = 3.9 ×103，流动分离被明显抑制，总升力系数脉动幅值明显减小，并呈周期性变化特性;对Re = 5.0 ×104，在圆柱体后方已不存在明显的脱落涡，总升力系数脉动幅值已很小。当N = 2.0 时，对Re = 3.9 ×103，尾涡已变为涡量幅值较小的小涡结构，总升力系数脉动幅值显著减小;对Re = 5.0 × 104，在圆柱体后方已产生射流现象，总升力系数的脉动幅值在零值附近小幅度波动。

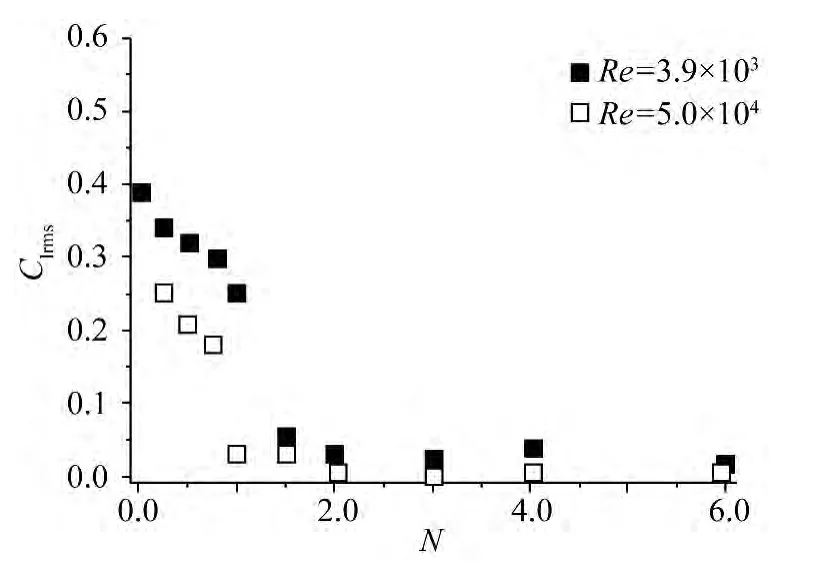
图13 圆柱体总升力系数均方值随电磁力作用参数变化特性Fig.13 Variation characteristics for the root mean square value of the total lift coefficient of the circular cylinder with the electromagnetic force interaction parameter

在图13 中，给出了电磁力作用下总升力系数均方值的数值结果。由图可知，随着电磁力作用参数的增大，总升力系数均方值随之减小，而且在某个临界电磁力作用参数后总升力系数均方值突然减小至接近于零。对Re = 3.9 × 103，当N ≤1.0 时总升力系数均方值随电磁力作用参数近似线性减小，在N ＞1.0 后总升力系数均方值显著减小且接近于零。对Re = 5.0 × 104，当N ≤0.75 时总升力系数均方值随电磁力作用参数近似线性减小，在N ＞0.75 后总升力系数均方值显著减小且接近于零。

3 结 语

对两个亚临界区雷诺数Re = 3.9 ×103和Re = 5.0 ×104，采用DES 方法数值模拟与分析了电磁力作用下圆柱体三维绕流场及其升阻力系数的变化特性。具体结论如下:

1)存在一个临界电磁力作用参数Nc1，当N ＜Nc1时，电磁力对圆柱绕流场三维特性的影响并不明显，在不同展向断面处流动分离角不同。当N ≥Nc1时，电磁力显著减弱圆柱绕流场的三维特性，在不同展向断面处流动分离角趋于相同。存在一个随Re 增大而减小的临界电磁力作用参数Nc2，在电磁力作用下当N =Nc2时流动分离角达到最大、然后消失，并当N ＞Nc2时在圆柱体尾部形成射流现象。

2)圆柱体总阻力由摩擦阻力和压差阻力构成，在电磁力作用下摩擦阻力随N 增大而增大，而压差阻力随N 增大而减小，但后者的减幅大于前者增幅，总阻力随N 增大而减小。在电磁力作用下随着Re 的增大总阻力减幅随着增大，而且在尾部形成射流现象后电磁力开始对圆柱体产生净推力作用。存在一个随Re 增大而减小的临界电磁力作用参数Nc3，当N ＜Nc3时升力系数均方值随着减小，而当N ≥Nc3时升力系数均方值显著减小且接近零。

［1］Williamson C H K. Vortex dynamics in the cylinder wake［J］. Annual Review of Fluid Mechanics，1996，28(1):477-539.

［2］Gad-el-Hak M，Bushnell D M. Separation control:review［J］. Journal of Fluids Engineering，1991，113(1):5-30.

［3］Zdravkovich M M. Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding［J］. Journal of Wind Engineering and Industrial Aerodynamics，1981，7(2):145-189.

［4］Kwon K，Choi H. Control of laminar vortex shedding behind a circular cylinder using splitter plates［J］. Physics of Fluids，1996，8(2):479.

［5］Li Z，Navon I M，Hussaini M Y，et al. Optimal control of cylinder wakes via suction and blowing［J］. Computers ＆ Fluids，2003，32(2):149-171.

［6］Atktin C J，Mughal M S. Parametric studies on the application of distributed roughness elements for laminar flow control［C］//35th AIAA Fluid Dynamics Conference Exhibit. Canada:［s.n.］，2005.

［7］陈 虹.分离流动的电磁力主动控制［D］.武汉:华中科技大学，2011. (CHEN Hong. Active control for separation flow by electromagnetic force［D］. Wuhan:Huazhong University of Science and Technology，2011.(in Chinese))

［8］Henoch C，Stace J. Experimental investigation of a salt water turbulent boundary layer modified by an applied streamwise magnetohydrodynamic body force［J］. Physics of Fluids，1995，7(6):1371-1383.

［9］梅栋杰，范宝春，陈耀慧，等. 槽道湍流展向振荡电磁力控制的实验研究［J］. 物理学报，2010，59(12):8335-8342.(MEI Dong-jie，FAN Bao-chun，CHEN Yao-hui，et al. Experimental investigation on turbulent channel flow utilizing spanwise oscillating Lorentz force［J］. Acta Phys. Sin.，2010，59(12):8335-8342. (in Chinese))

［10］Weier T，Gerbeth G，Mutschke G，et al. Experiments on cylinder wake stabilization in an electrolyte solution by means of electromagnetic forces localized on the cylinder surface［J］. Experimental Thermal and Fluid Science，1998，16(1-2):84-91.

［11］Oliver P，Roger G. Electromagnetic control of sea-water flow around circular cylinder［J］. European Journal of Mechanics-B/Fluids，2001，20(2):255-274.

［12］周本谋，范宝春，陈志华，等. 圆柱表面包覆电磁场消涡与增涡实验研究［J］. 实验力学，2004，19(2):242-247.(ZHOU Ben-mou，FAN Bao-chun，CHEN Zhi-hua，et al. Experiments on vortex suppression and vortex acceleration by means of electromagnetic field localized on the cylinder surface［J］. Journal of Experimental Mechanics，2004，19(2):242-247. (in Chinese))

［13］ZHANG Hui，FAN Bao-chun，CHEN Zhi-hua. Optimal control of cylinder wake by electromagnetic force based on the adjoint flow field［J］. European Journal of Mechanics B/Fluids，2010，29(1)，53-60.

［14］张 辉，范宝春，陈志华. 电磁激活板宽度对圆柱绕流控制的影响［J］. 工程力学，2007，24(12):164-168. (ZHANG Hui，FAN Bao-chun，CHEN Zhi-hua. Cylinder wake flow affected by width of electromagnetic actuator［J］. Engineering Mechanics，2007，24(12):164-168.(in Chinese))

［15］ZHANG Hui，FAN Bao-chun，CHEN Zhi-hua. Computations of optimal cylinder flow control in weakly conductive fluids［J］.Computers ＆ Fluids，2010，39(8)，1261-1266.

［16］ZHANG Hui，FAN Bao-chun，CHEN Zhi-hua，et al. Effect of the Lorentz force on cylinder drag reduction and its optimal location［J］. Fluid Dynamics Research，2011，43(1):1-18.

［17］尹纪富，尤云祥，胡天群，等. 电磁极板宽度对圆柱绕流场影响的数值分析［J］. 力学学报，2013，45(4)，493-506.(YIN Ji-fu，YOU Yun-xiang，HU Tian-qun，et al. Numerical analysis for the effect of the electromagnetic force actuator width on flow structures around a circular cylinder［J］. Chinese Journal of Theoretical and Applied Mechanic，2013，45(4):493-506. (in Chinese))

［18］Kim S J，Lee C M. Investigation of the flow around a circular cylinder under the influence of an electromagnetic force［J］.Experiments in Fluids，2000，28(3):252-260.

［19］Kim S J，Lee C M. Control of flows around a circular cylinder:suppression of oscillatory lift force［J］. Fluid Dynamics Research，2001，29(1):47-63.

［20］Travin A，Shur M，Strelets M，et al. Detached-eddy simulations past a circular cylinder［J］. Flow，Turbulence and Combustion，2000，63(1-4):293-313.

［21］Squires K D. Detached-eddy simulation:current status and perspectives［M］//Direct and Large-Eddy Simulation V. Springer Netherlands，2004:465-480.

［22］Elmiligui A，Abdol-Hamid K S，Massey S J，et al. Numerical study of flow past a circular cylinder using RANS，hybrid RANS/LES and PANS formulations［C］//22nd Applied Aerodynamics Conference and Exhibit. 2004:AIAA 2004-4959.

［23］Benim A C，Pasqualotto E，Suh S H. Modelling turbulent flow past a circular cylinder by RANS，URANS，LES and DES［J］.Progress in Computational Fluid Dynamics，2008，5(8):299-307.

［24］Ong M C，Utnes T，Holmedal L E. Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers［J］. Marine Structures，2009，22(2):142-153.

［25］Norberg C. Flow around a circular cylinder:aspects of fluctuating lift［J］. Journal of Fluids and Structures，2001，15(3):459-469.

［26］Norberg C. Effects of reynolds number and a low-intensity freestream turbulence on the flow around a circular cylinder［D］.Sweden:Chalmers University of Technology，1987.