广义误差分布下CVaR模型的股市风险研究

朱翔翔， 姚 俭

（上海理工大学 管理学院，上海 200093）

金融业管制的放松和金融自由化的发展导致了全球金融市场波动的加剧，金融机构面临着日趋严重的金融风险.目前，金融市场风险测度的主流方法是由Morgan提出的风险价值VaR（value at risk）.该指标不仅被金融机构用于风险管理，而且被众多金融监管组织作为风险评估的标准.巴塞尔银行监管委员会还在“1996年巴塞尔修正案”中利用VaR所确定的市场风险来规定银行及其它金融机构的资本充足率.我国学者杜海涛［1］在市场指数风险量度、单个证券的风险度量、基金管理人员绩效评价及确定配股价格等方面运用VaR 方法，验证了VaR 模型对风险的测度效果较好.尽管VaR 指标在实践中得到广泛的应用，但其本身存在着诸多的理论缺陷，如VaR 不满足一致性风险测度理论中次可加性的公理，这使得基于VaR 的资产组合无法通过分散化投资降低投资风险［2］.因此，人们提出了许多不同的风险测度指标，其中，条件风险价值 CVaR（conditional value at risk）满足一致性风险测度理论，在性质上优于VaR 指标［3］.同时，金融资产收益波动率的测度及其动力学特征的刻画，对基于VaR，CVaR 指标的金融市场风险测度具有十分重要的理论意义.目前的理论研究中存在多种不同的模型描述方法可以用于刻画金融资产收益波动率，究竟哪一种模型最适合我国股票市场的实际波动特征和风险状况尚无定论.实证研究发现［4］，我国金融资产的收益率序列普遍不服从独立同分布假设且不服从正态分布，存在着波动集聚（volatilityclustering）和厚尾（fat－tail）的特性，具有很强的自回归条件异方差（ARCH）效应.因此，可以运用广义自回归条件异方差模型（GARCH 模型）对沪深300指数的波动率进行估计.另外，在采用极大似然估计GARCH 模型时，通常假定误差服从正态分布，但此种假设不能反映我国金融收益序列的特征，一般可以通过假定收益率序列服从具有尖峰厚尾特征的分布，如广义误差分布（GED）来解决［5］.广义误差分布可以通过其参数的调整拟合出不同的分布形式，使用更为灵活，对数据分布的刻画也更准确.

基于以上认识，本文通过运用GARCH 模型为我国股票市场收益的条件波动率建模，同时选择对金融资产收益率分布典型特征具有较强描述能力的广义误差分布来刻画沪深300指数收益率的分布特征.在此基础上计算不同风险测度模型的风险价值VaR 和条件风险价值CVaR，并运用返回检验方法检验VaR 和CVaR 两种指标的准确性，探讨适用于我国股票市场的风险测度方法.

1 数据选取与检验

沪深300指数是由沪深证券交易所联合发布的反映我国A 股市场价格波动和运行状况的重要指数.选取沪深300 指数为研究样本，选择2005年1月4日至2012年6月29日的每日收盘价格指数，共计1 816个数据.估计时对指数数据进行自然对数处理，计算指数的日收益率

式中，Rt代表时间t 的日收益率；Pt代表时间t 的收盘价格指数.

图1给出了2005年1月5日至2012年6月29日的每日收益率序列图.从图1中可以直观地看出，收益率序列显示出一定的波动聚集现象.

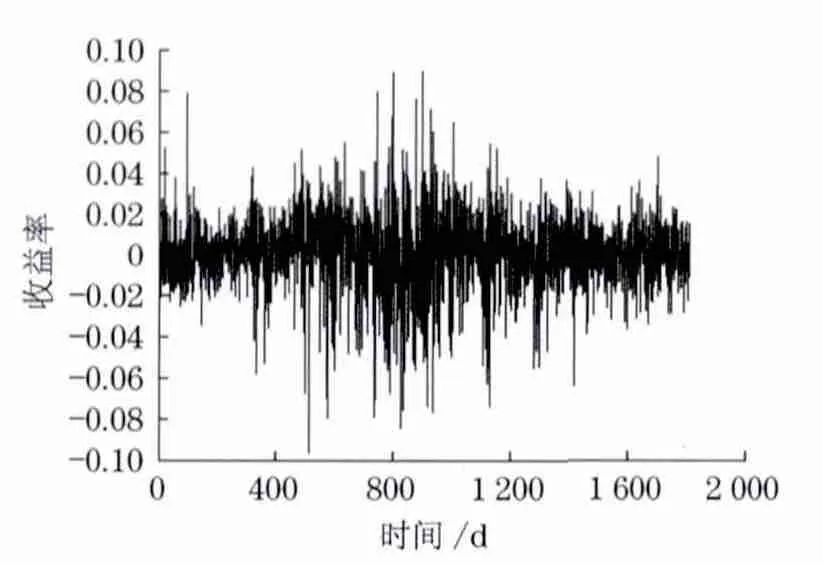
图1 沪深300指数每日收益率序列Fig.1 Time series of daily return rate of CSI 300index

使用Engle 提出的拉格朗日乘数检验，即ARCH LM 检验，对原始收益数据进行ARCH 效应检验.表1为ARCH LM 检验结果.R 为可决系数，n为样本量.

表1 异方差性检验：ARCH 效应Tab.1 Heteroskedasticity test：ARCH effect

表1中F 统计量和LM 统计量均十分显著，说明拒绝收益序列没有自相关的假设，暗示收益波动具有ARCH 效应，所以，可以利用GARCH 模型进行波动率的建模.

图2将样本数据频率图与正态分布对比，指数每日收益率呈现出明显的尖峰厚尾现象，并不满足正态分布的假设.

图2 指数每日收益率分布与正态分布对比图Fig.2 Comparison between return rate distribution and normal distribution

另外，运用迪基－福勒检验（ADF test）检查数据的平稳性.从表2结果可以看出，收益率序列满足平稳性假设，可以直接用于下一步的计量建模.

表2 收益率序列ADF单位根检验Tab.2 Unit root test of return rate series by ADFtest

2 我国股票市场波动率模型及估计

2.1 我国股票市场波动率模型

在金融时间序列中经常发生某一特征的值成群出现，即资产收益率大的变化（正的或负的）后，往往随后会有大的变化，小的变化（正的或负的）后会发生小的变化，这就是波动聚集效应.图1显示，沪深300指数收益率具有明显的波动聚集效应.针对这一现象，Engle 提出了自回归条件异方差模型（ARCH 模型），很好地刻画了金融时间序列的这种特征［6］.但由于在非负参数约束下求解极大似然估计，对参数进行估计有一定的困难，Bollerslev又提出了广义的ARCH 模型，即Generalized ARCH 模型（GARCH 模型），他在条件方差的方程中加上了自回归项，用简单的GARCH 模型代表一个高阶的ARCH 模型，弥补了ARCH 模型的不足，大大减少了待估的参数，使得方程更加简约，避免了过度拟合［7］.Engle和Patton的研究结果表明［8］，实证研究中GARCH（1，1）模型是权衡计算精度和模型复杂程度的一种比较合适的折中，因此，现假定条件方差满足GARCH（1，1）模型.

式 中，rt为 指 数 收 益 率；ut为 残 差；μt 为 收 益 率 的 条件均值；εt为满足独立同分布且服从标准正态分布的随机变量；α0，α1，β1 为系数.

考虑到我国沪深300指数收益率存在的尖峰厚尾现象（如图2所示），采用一种较为灵活的、能够同时刻画这两种特征的GED 来表示εt的分布情况.GED 的密度函数为

式中，Γ（ ）· 为伽马分布；v为GED 分布参数.

通过对参数值v 的调整，GED 可以表示出不同程度的尖峰厚尾.当v＝2时，GED 即为标准正态分布；当v＜2时，广义误差分布比正态分布具有更厚的尾部和更尖的峰，而且随着v值的减小，尖峰厚尾现象越明显，即极端事件出现的概率随v 的减小而增大；当v＞2时，其尾部则较正态分布更薄.

同时，为了验证GED 分布假设对波动率方程估计的影响，还将对正态分布假设下的波动率方程进行估计.两种不同的情况分别记为GARCH（1，1）－GED，GARCH（1，1）－N.

2.2 波动率模型的参数估计

运用Eviews软件对两种波动率模型进行参数估计，结果如表3和表4所示.

表3 估计GARCH（1，1）－GED 模型结果Tab.3 GARCH（1，1）－GED model estimation and results

表4 估计GARCH（1，1）－N 模型结果Tab.4 GARCH（1，1）－N model estimation and results

从表3和表4的估计结果可以看出，条件方差方程中3项的系数均高度统计显著.此外，与典型的金融资产收益GARCH 估计相似的是，这里滞后一期的误差平方项与滞后条件方差系数的和接近于1.这表明冲击对条件方差的影响具有很强的持续性.截距项μt 很小，而滞后条件方差系数β1 很大，为0.9，意味着在一段时间内，大的正或负收益会导致大的方差预测值［9］.

对GARCH（1，1）－GED 模型估计的残差再作ARCH LM 检验，从表5（见下页）的检验结果发现，残差序列已经不存在显著的异方差现象，所以，上述模型较好地刻画了我国股票市场沪深300指数收益率序列的波动率特征.

表5 异方差性检验：ARCH 效应Tab.5 Heteroskedasticity test：ARCHeffect

3 风险测度值的计算及返回检验

3.1 风险测度值的计算

运用参数法计算VaR 值.在置信水平α 下，可以写出t时刻的VaR 值为

式中，pt－1代表滞后一期的指数值；zα表示在给定置信水平α 下的分位数；σt可由GARCH 模型先求出，进而开方得出相应的标准差σt.

取置信水平99%计算VaR 指标序列.

若用zα表示对应于某一置信水平α 的分位数，用q表示大于zα的分位数.根据CVaR 的定义可知CVaR 值为［10－11］

式中，pt－1表示第t－1日的指数收盘价格；f（q）表示收益率序列服从分布的密度函数.

在GED 条件下，CVaR 值为

在正态分布条件下，CVaR 值为

3.2 不同风险测度值的返回检验

对VaR，CVaR 进行返回检验分析主要是检验其对风险（实际损失）的覆盖情况［12］.本文采用Kupiec于1995年提出的失败频率检验法.当损失超过风险测度值时，记为一次测度失败，则失败率PL＝N／T.其中，T 为实际考察天数，N 为失败的天数.理论上每次观察到的失败次数服从概率为P＊L＝α的伯努利分布，所以，对风险测度值的检验便可以转化为检验PL是否显著等于P＊L.基于这一推论，Kupiec提出了似然比检验LR.

若零假设是正确的，则似然比满足自由度为1的χ2分布，也就是说，在置信水平α上，如果所计算的LR 统计量大于该水平上自由度为1的χ2分布的临界值，则应该拒绝原假设；反之，则应该接受原假设，即认为所采用的风险测度模型足够准确［13］.

计算在99%的置信水平下基于GARCHGED 和GARCH－N 模型的两种不同风险测度值.模型对风险状况预测结果的返回检验采用最为常见的“失败率”检验.由Matlab软件计算，得到结果如表6所示.

表6 99%置信水平下VaR，CVaR 模型的返回检验Tab.6 Back test of VaR and CVaR model at 99%confidence level

从表6的返回检验结果可知：a.基于GED 的两种风险测度值均要好于基于正态分布的情况，因此，可以认为，目前研究中所采用的正态分布假设并不适用于我国股票市场的风险测度，而使用具有尖峰厚尾特征的GED 有助于提高对市场极端风险的估计精度.b.在99%置信水平下，基于相同的分布假定和GARCH 模型，CVaR 的失败天数和失败率均小于相应的VaR 的失败天数和失败率.由LR 统计量来看，只有GARCH（1，1）－N－VaR 模型未通过检验.其它3个模型的失败天数均处于可接受的范围内.因此，综合考虑对我国股票指数收益率波动的刻画以及VaR，CVaR 指标对风险的估计精度，结合GARCH（1，1）－GED 的CVaR 模型对我国股票市场的风险测度较为合理.

4 结 论

以沪深300指数为研究样本，对我国股票市场指数收益率的波动特点进行了研究，结果表明，GARCH（1，1）－GED 模型可以很好地刻画收益序列的波动率.在此基础上对股市风险进行测度，实证分析了4种风险测度模型，并运用返回检验的方法对比了不同模型风险测度指标的精度，最终得出结论，在相同的收益率分布假定下，CVaR 指标对风险的测度更为准确、合理，说明CVaR 值对风险的容忍度更低，更加客观保守，也更加符合风险管理的谨慎性原则，对我国金融市场的风险管理以及市场监管工作具有一定的借鉴意义.

［1］杜海涛.VAR 模型在证券风险管理中的应用［J］.证券市场导报，2000（8）：57－61.

［2］Artzner P，Delbaen F，Eber J，et al.Thinking coherently［J］.RISK，1997，10（11）：68－71.

［3］Artzner P，Delbaen F，Eber J，et al.Coherent measures of risk［J］.Math Fin，1999，9（3）：203－228.

［4］陈守东.VaR 的一种模拟方法［J］.决策借 鉴，2000，3（3）：32－33.

［5］吴晓霖，蒋祥林，孙绍荣.基于广义期望效用理论的主观概率调整的一致性风险测度［J］.上海理工大学学报，2010，32（5）：479－487.

［6］Engle R F.Autoregressive conditional heteroskedasticity with estimates of the variance of united kingdom inflation［J］.Econometrica，1982，50（4）：987－1008.

［7］Bollerslev T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986（31）：307－327.

［8］Engle R F，Patton A J.What good is a volatility model？［J］.Quantitative Finance，2001，1（5）：237－245.

［9］Brooks C.金融计量经济学导论［M］.邹宏元，译.成都：西南财经大学出版社，2005.

［10］文凤华，马超群，陈牡妙，等.一致性风险价值及其算法与实证研究［J］.系统工程理论与践，2004，24（10）：15－21.

［11］赵静，肖庆宪.条件风险价值度量方法在银行投资组合优化中的应用［J］.上海理工大学学报，2005，27（5）：389－392.

［12］王鹏，鹿新华，魏宇，等.中国金融期货市场的风险度量及其Back testing分析［J］.金融研究，2012（8）：193－206.

［13］江涛.基于GARCH 与半参数法VaR 模型的证券市场风险的度量和分析：来自中国上海股票市场的经验证据［J］.金融研究，2010（6）：103－111.