有强带C-根的半群
李慧明, 高振林, 刘皖平
(上海理工大学 理学院,上海 200093)
1 预备知识
半群S 上的格林关系L,R,D,H,J 定义[1]为
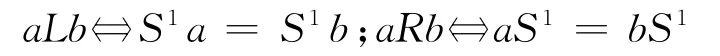
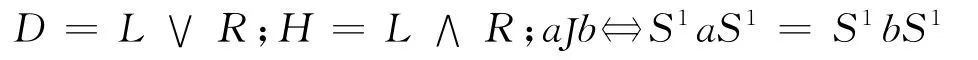
性质1[1]a.对于半群S, ( )R L 是S 上左(右)同余;
b.设H 是半群S 的子半群,则
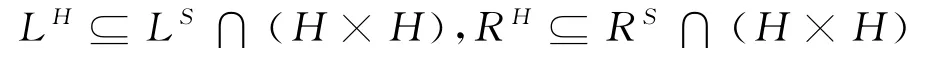

若H 是半群S 的正则子半群,以上成相等包含关系.
半群S 称 为Clifford 半 群[1](简 称 为C-半群),若S 是正则半群且幂等元均为中心幂等元,即E(S)⊆C(S).半群S 称为右(左)正则半群,若对右(左)正则半群S 称为充足的,若对显然,正则半群既为左正则半群又为右正则半群.半群S 称为右(左)逆半群[2-3],如果S 是正则半群,且对∀a∈S,有
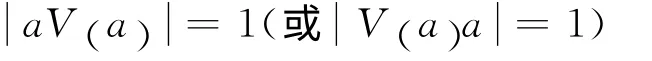
V(a)表示a 的所有正则逆元集.半群S 称为左Clifford 半群[4](简称为左C-半群),若S 是充足右正则半群且aS⊆L(a)(∀a∈S).文献[4]指出,C-半群S 是左C-半群,反之不必.左(右)零带Iα(Λα)与群Gα的直积Iα×Gα(Λα×Gα)称为左(右)群带[2-3].称半群直积S1×S2为半格织积,记为S1×sspS2,若S1,S2有共同的半格同态像.文献[1-6]证明了以下引理.
引理1 a.在充足左(右)正则半群S 中,对∀a∈S,∃|幂等元,记为a+(a*),使得
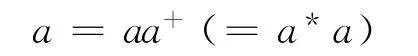
b.左(右)逆半群S 为充足右(左)正则半群;
c.左C-半群S 为完全正则左群带的半格,反之不必;
d.左(右)群带的半格S 是右(左)逆半群,且S同构于左正则带I( )∧ 与C-半群T 的半格织积,记为S≅I×sspT(Λ×sspT);
e.半群S 是C-半群当且仅当S 是J-类子群的半格,即S=∪α∈YGα
定义2 对于半群S,若S 上没有任何C-同余,则定义S 上的泛关系S×S 为S 上的C-根同余,且称S 为C-根半群.若S 上至少有一个C-同余,则定义S 上所有C-同余ρα(α∈ω)的交为S 上C-根同余,记作ρcr.即
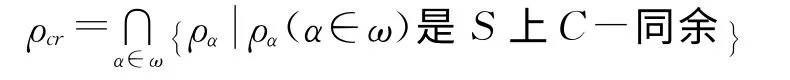
C-根同余ρcr可能不再是C-同余.但以下结论是易见的.
引理2 若ρcr仍是S 上C-同余,则它是S 上最小C-同余.反之,若S 上C-同余ρ是S 上最小C-同余,则ρ=ρcr.
定义3 设ρ是半群S 上一个同余,若存在S的子集H,使得S=H∪C,且C 同构于则称H是S 的ρ-集.此时,将ρ记作ρH.
定义4 若半群S 上C-根同余ρcr有ρcr-集,则将ρcr-集记作N(S).称N(S)为S 的C-根集.这时有ρcr=ρN(S).因此可将C-根同余ρcr和C-根集N(S)统称为S 的C-根.
定义5 如果ρcr仍是半群S上C-同余,且S的C-根集N(S)存在,则称C-根ρcr是强C-根.
命题1 设半群S 有强C-根ρcr,则根集N(S)可表为是S 的C-同余ρα-集}
由引理1知,左(右)逆半群与左C-半群均为正则半群.文献[1-6]讨论的均为这类半群的子类.本文试图用文献[1]中关于半群的根描述,引进另-类正则半群,称之为有强带C-根的半群.证明左(右)群带的半格半群、左C-半群均为有强带C-根的半群.并用实例证明,存在这种半群,它不是以上半群.通过讨论强(带)C-根与有强带C-根的半群的性质,用织积手段给出有强带C-根的半群的结构特征.
2 有强带C-根半群的概念及相关性质
定义6 若半群S 有强C-根ρcr,且 ( )N S =E( )S 是带,则称S 为有强带C-根半群.
引理3 设S 为有零元的左(右)群带的半格半群,则以下各条成立:
a.L=J(R=J)是S 上半格同余;
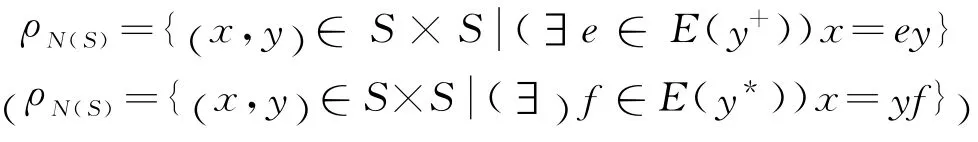
这里E(x+)(E(x*))(x∈S)表示元x+(x*)生成的矩形带.
证明 由定义,设
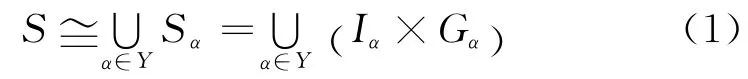
这里Y 是半格,Sα=Iα×Gα(α∈Y)是左群带,令则I,T 分别是S的有零元左正则子带与C-子半群,其中T*=∪Gα是S 的无零元C-子半群,且S=E (S ) ∪
a.由式(1)知,在S 上
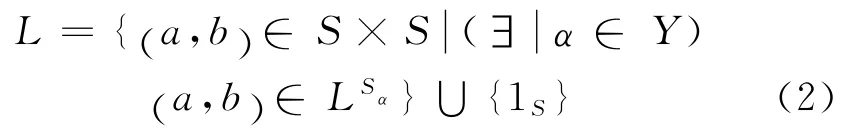
而在左群带(∀α∈Y)Sα上,由文献[2]知,LSα是半格同余,且LSα=JSα.因此,由式(2)得引理3中结论a.
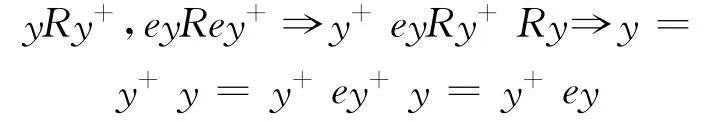
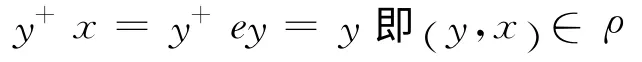
ρ具有对称性.若
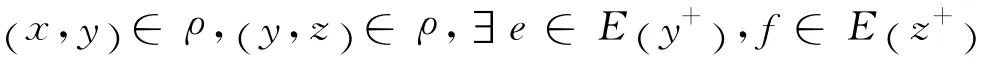
使得x=ey,y=fz.
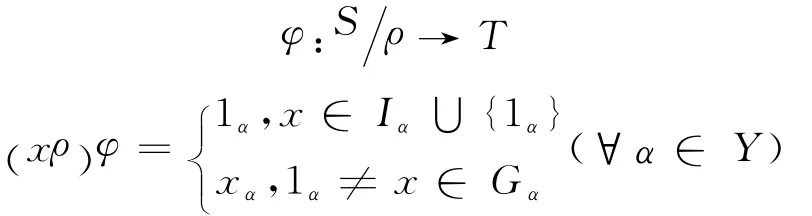
最后证ρ是S 上的最小C-同余,从而由引理2知ρ=ρcr,且N(S)=E(S):设σ是S 上仼一个C-同余,若则于是
类似的可以证明对有零元右群帯的半格半群,相应结论也成立.证毕.
下例证明,有强带C-根的半群是借C-半群通过根理论真扩张得到的半群类.
例1 取一个有零元的带B,B 不是仼何特殊带.由带结构,设B 表成矩形带Bα的半格Bα,这里半格再用半格Y 作有零元C-半群其中是群,由于半格故令S=B∪T,则规定S 上运算
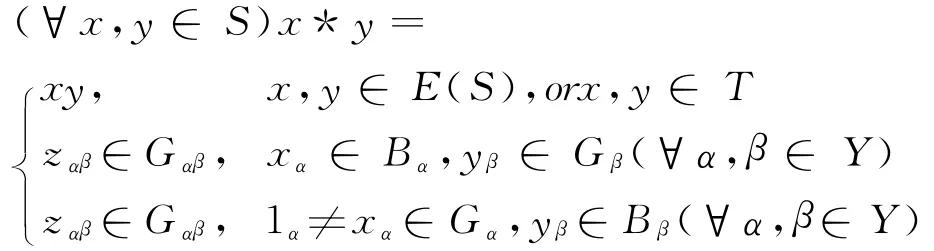
经验证S 关于以上运算成半群.釆用引理3完全相同证法,可证S 是有强带C-根的半群,且
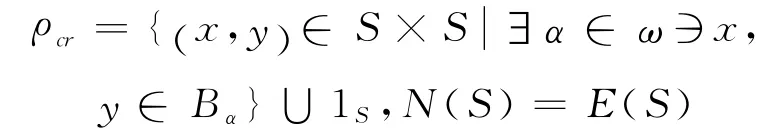
由于B 不是左、右正则带,从而S 不是右或左逆半群,当然不是右或左群带的半格半群.
以下S 总表示含零元的有强带C-根的半群.由文献[1]中带的结构定理,设S 的C-根集N(S)是S 的J-类子矩形带Bα(∀α∈ω)的半格,即由引理1,设S 的没有零元的C-子半群T*是S 的J-类子群的半格,即T*可表为由定义6,S 可表为
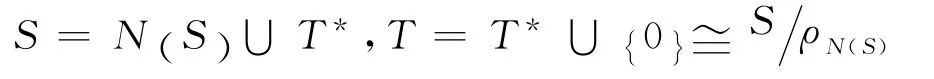
c.S 是充足右(左)正则半群,且
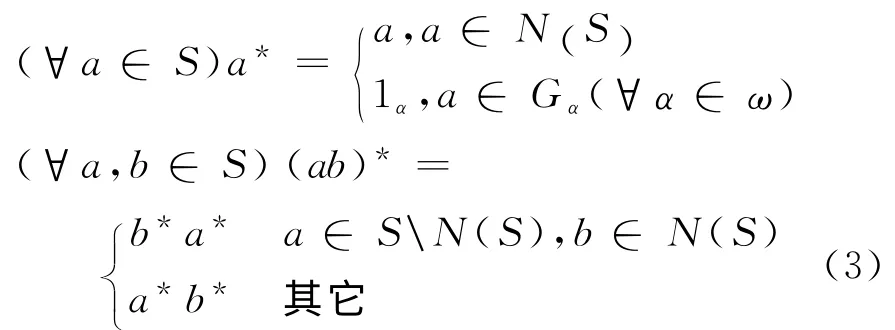
证明 a.因i∈Bα,1β∈Gβ且1β∈Bβ,由于Bα,Bβ是矩形带,故1βi∈Bβα.又对∀x∈Gβ,i1βx=ix,若不可能,故
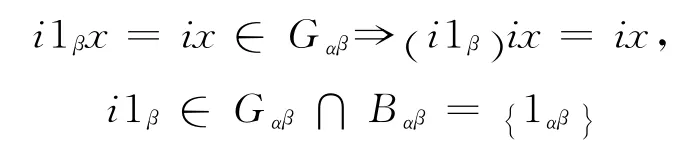
所以,i1β=1αβ.由此推得i=i1αi=1αi.
b.因i∈Bα,a∈Gβ,则由性质2中结论a得
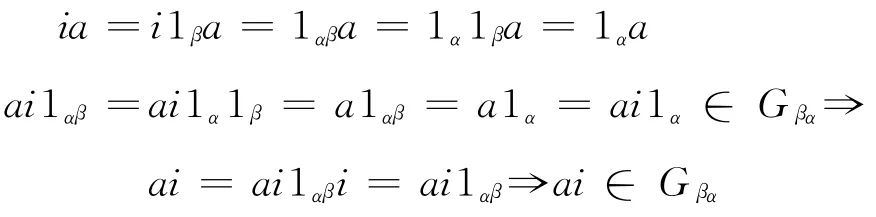
c.对∀a∈S,显然a=a*a=aa*,a*∈La成立.若有当时,a可逆,由ae=aa*⇒e=a*=1α.当a∈Bα(α∈ω)时,由ae=aa*,ea=a*a⇒e=eae=a*aa*=a*.故S 是充足右正则半群.往证式(3)成立:设a,b∈S,分4种情形:Bβ.由性质2 中结论a计算知,对情形有对情形(d)有
同样可证S 是充足左正则半群.证毕.
性质3 a.S 是正则半群;
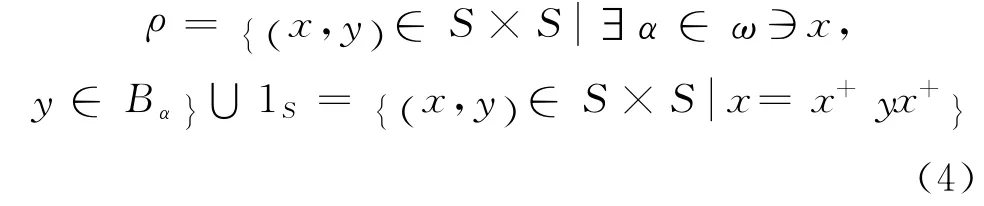
b.该结论是易见的.
c.由性质3中的结论a、性质1得
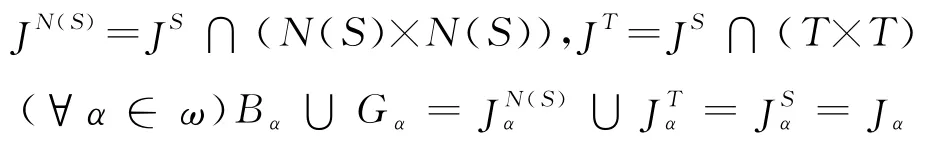
这里JαH表示子半群H 上格林关系JH的一个JH-类.
d.先证L 是同余:由性质1,L 是右同余.设
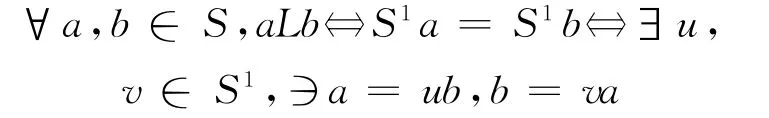
于是∃α,β∈Y(orα,β∈ω,orα∈Y,β∈ω)∍α=αβ=βα=β.即可设
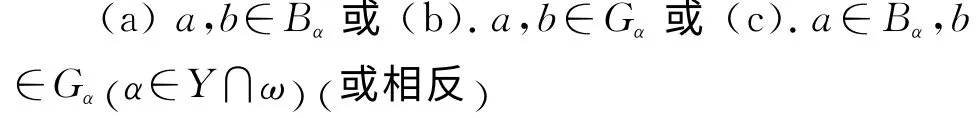
对以上情形分别证明如下:
(a).若a,b∈Bα,由性质3中的结论c知L|N(S)=J|N(S),L|T*=J|T* 分别是N(S)与T*上半格同余.若对T*则caLcb成立.由性质2知,情形∀c∈S,ca∈N(或相反)不可能出现.
(b)若a,b∈Gα,由性质2知,对∀c∈S,ca,cb∈T*.同上,caLcb.
(c)若a∈Bα,b∈Gα(α∈Y∩ω)(或相反),由性质2 知,对∀c∈S,cb∈T*.若c∈T*,则ca∈T*,从而caLcb成立.若则ca∈Bβα(∃β∈Y⊆ω).此时cb∈Gβα.由性质3中结论c知,与ca,cb在同一个L-类,即caLcb.综上,L 是S 上同余.
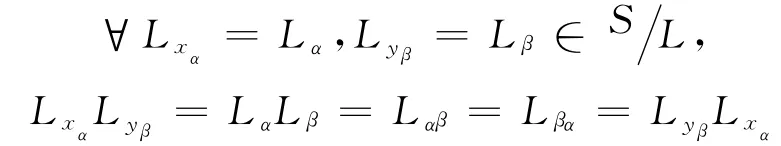
再证L=J:显然,L⊆J.只要证反包含.设aJb(a,b∈S),则
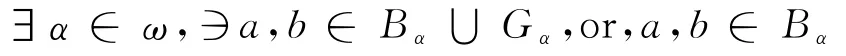
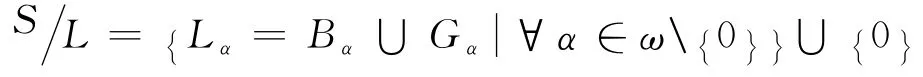
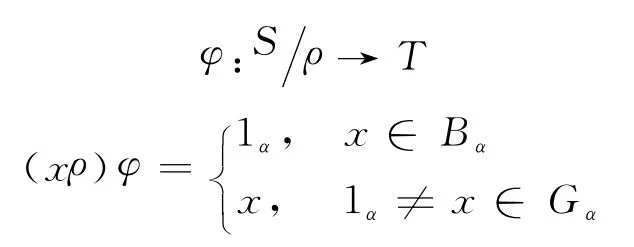
再证ρ是S 上最小C-同余,从而由引理2知ρN(S)=ρ:设σ是S 上仼一个C-同余则有或x=y.若后者成立,显然设前者成立,因为σ是S 上C-同余,故有xσ=1ασ=yσ,从而也有综合得
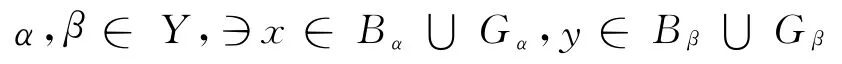
由x =x*yx*得α =αβ.又 由y*xy*=y*x*yx*y*=y*x*y*yy*x*y*=y*yy*=y,得β=αβ,β=α,x,y ∈Bα∪Gα.若x,y ∈Bα,则
若1α≠x,1α≠y∈Gα,则x=x*yx*=1αy1α=y,从而若x∈Gα,y∈Bα(或相反),则由x=x*yx*知x=x*yx*=x*=1α.即同样由y*xy*=y 证明另情形.综合得即反 之,设则 有x,y ∈Bα或x=y.若后者成立,显然设前者成立,由于Bα是矩形带,故∃e,f∈Bα,使得x=eyf=ef.由于x=x*=(eyf)* =fy*e=fe=ef,从而e=f=x*,即故ρ⊆σ,从而ρ=σ.证毕.
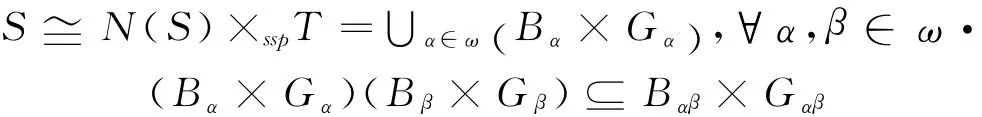
证明 a.设a,b∈S,aρN(S)b,由式(4)得a,b∈或a=b.若是后者,显然有aLb,若是前者,由于Bα=Lα,故也知aLb.

c.由S 满足的条件知,半格织积半群N(S)×sspT≙W 是可以做成的.令映射
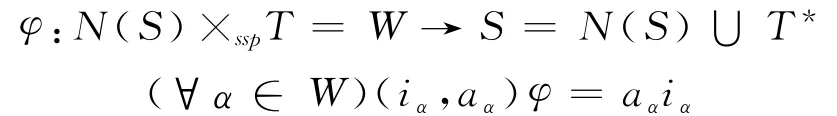
可证φ 是同构映射:对∀x∈S,∃α∈ω,∍x=iα∈Bα,or,x=aα∈Gα.若是前者,由性质2,1αiα=iα.于是若是后者,则有
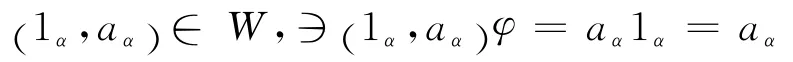
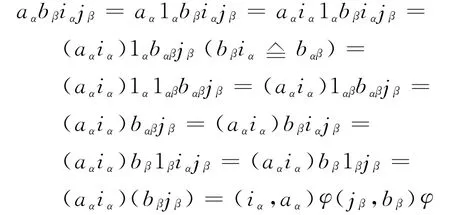
故φ 是同构映射.
3 有强带C-根半群的结构特征
定理1 设S 为正则半群,以下各条件等价:
a.S 为有强带C-根的半群;
b.L=J 是S 的半格同余,且由式(4)给出的关系是S 上的C-同余.
证明 (a)⇒(b)若S 为有强带C-根的半群,由性质3中结论d,e即得定理1中的结论b.
(b)⇒(a)若L=J 是S 的半格同余,且式(4)给出的关系ρ是S 上的C-同余,只需要证ρ 是S上最小C-同余,则由引理2,性质3即知,ρ=ρcr是S 的C-根且ρcr是强的.假设σ 是S 上C-同余,则有或x=y.若后者成立,显然设前者成立,因为σ是S 上C-同余,故有xσ=1ασ=yσ,从而也有综合得
[1]Howie J M.Anintroduction to semigroup theory[M].London:Academic Press,1976.
[2]Bailes G L.Right inverse semigroups[J].Journal of Algebra,1973,26(3):492-507.
[3]Liu L J,Li J F,Liu Z N.A construction of left inverse semigroups[J].Journal of Xiangtan Normal University(Natural Science Edition),2003,25(4):10-13.
[4]朱聘瑜,郭聿琦.左C-半群的特征与结构[J].中国科学,1991,21(6):582-590.
[5]Fountain J B.Adequatesemigroups[J].Proceedings of the Edinburgh Mathematical Society,1979,22(2):113-125.
[6]郭聿琦,任学明,岑嘉评.左C-半群的又一结构[J].数学进展,1995,24(1):39-43.

