基于改进PSO 算法的含风电场电力系统网架扩展规划研究

周建华，孙 蓉，陈久林，袁 越，袁晓冬

(1.江苏省电力公司电力科学研究院，江苏南京 211103；2.河海大学可再生能源发电技术教育部工程研究中心，江苏南京 210098)

风电大规模并网发电后，部分输电线路容易出现输电阻塞现象[1，2]。为缓解可能出现的输电阻塞，网架扩展规划是一个比较好的解决办法。该办法是依据仿真计算结果，通过在可能的线路走廊上扩建或新建线路，以实现缓解输电阻塞的目的。

在仿真计算中，算法的研究是整个网架扩展规划中非常重要的一个环节。总的来说，算法大致可分为解析类算法和人工智能类算法。较为常见的解析类算法有最小生成树法[3]、Benders 分解法[4]、分支定界法[5]等。由于网架扩展规划问题属于大规模数学组合问题，故该类算法存在计算时间长、对实际大规模系统求解困难等诸多缺点。此外，有些约束条件难以用数学模型表达，故由解析类算法求出的数学意义上的最优解未必是符合实际要求的最优方案[6]。人工智能类算法，目前主要有Tabu 搜索法[7]、遗传算法[8]、蚁群算法[9]、模拟退火算法[10]、离散猴群算法[11]、禁忌搜索法[12]、粒子群优化（PSO）算法[6]等。其中，PSO 算法通过记忆与反馈机制实现了高效的寻优搜索，对于求解网架扩展规划问题中那些目标函数或约束条件不可微的非线性优化问题尤为适用。

利用PSO 算法寻找含风电场电力系统最优的网架扩展规划方案时，有2个问题值得关注：一是容易陷入局部最优解；二是收敛速度缓慢。基于以上认识，文中研究了含风电场电力系统网架扩展规划问题，提出了同时动态优化调整惯性权重和学习因子的改进PSO 算法。

1 含风电场电力系统网架扩展模型

利用网架扩展规划来缓解系统输电阻塞，其本质是通过线路的扩建或新建，将那些重负荷线路上输送的部分功率由其他轻负荷线路来输送。在假定所有线路输送容量极限一致的前提下，也就意味着需要尽可能地使所有线路上输送的有功功率相差不大。与此同时，在衡量某系统是否发生输电阻塞时，节点电压幅值大小也是一个依据。若某节点电压幅值介于正常范围时，该节点所连接的线路发生输电阻塞的可能性就会比较低。反之，若超出正常范围时，该节点所连接的线路很可能是重负荷线路，这时系统极有可能发生阻塞。

基于上述认识，文中的目标函数定义为：

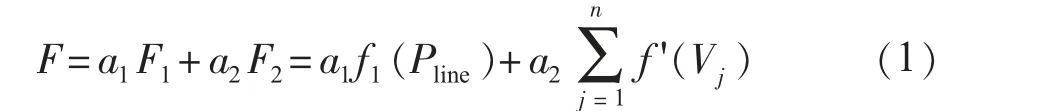
其中：

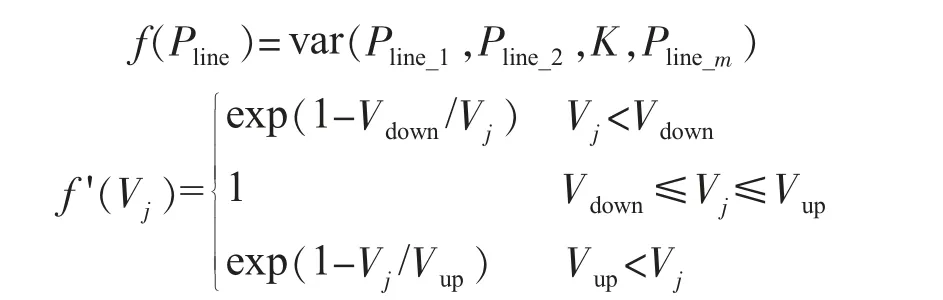
式中：a1，a2为常数，用于调整不同指标在目标函数中所占的比例；Pline_i为第i 条线路上输送的有功功率，i=1，2，K，m，m为线路总数；Vj为节点j的电压幅值，j=1，2，K，n，n为节点总数；Vup，Vdown分别为节点电压幅值上、下限。约束条件为系统常规潮流方程，如式（2）、（3）所示：

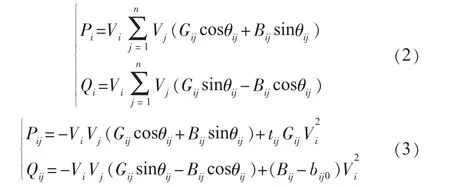
式中：Pi，Qi分别为节点i的有功功率和无功功率注入量；θij为节点i 和节点j 上电压角度的差值；Gij，Bij分别为导纳矩阵元素的实部和虚部；tij为变压器变比；bij0为线路导纳的一半。

2 改进的PSO 算法

PSO 算法源自鸟群捕食行为的研究，是一种通用的启发式搜索技术。自提出以来，该算法就以概念简单、容易实现和需要调整的参数较少等优点得到了广泛应用和研究。

2.1 PSO 算法及惯性权重计算策略

PSO 算法的基本思想是[13]：随机初始化一群没有体积和质量的粒子，将每个粒子视为优化问题的一个可行解，粒子的优劣由一个事先设定的适应度函数来辨别。每个粒子在可行解空间内运动，并由一个位移变量决定其迭代的方向。

粒子k 在t+1时刻的位置zt+1k 可以通过下式更新获得：

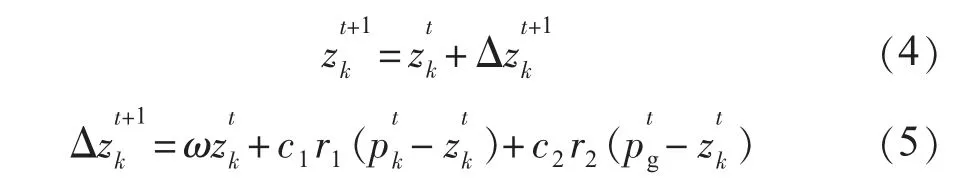
式中：ω为惯性权重；c1，c2为学习因子（通常设置为常数）；r1和r2是均匀分布在（0，1）区间的随机数；分别是所有粒子和粒子k 从第一次迭代至当前迭代次数内出现的最优解。

式（5）由三部分组成：第一部分表示粒子对当前自身运动状态的延续，依据自身的位置进行惯性运动；第二部分表示粒子的思考，即综合考虑自身以往的经历从而对下一步行为进行决策，反映的是增强学习过程；第三部分表示粒子间的信息共享和相互合作。在搜索过程中，每个粒子一方面要记住自己的经验，同时还要考虑同伴的经验。当单个粒子觉察同伴经验较好的时候，它将进行适应性的调整，寻求一致认知过程。

在标准PSO 算法中，惯性权重是重要的参数，决定了粒子先前位置对当前位置的影响程度。惯性权重值较大，有利于全局搜索，虽然搜索速度快，但不易得到精确解。反之，惯性权重值较小，有利于局部搜索和得到更为精确的解，但收敛速度慢，有时会陷入局部极值。因此，寻找合适的惯性权重值，使之在搜索精度和搜索速度方面起恰当的协调作用，成为很多学者研究的焦点。

文献[14]将惯性权重随着迭代次数而线性递减，计算公式为：

式中：ωstart为惯性权重的初始值，也是最大值；ωend为迭代结束时的惯性权重值，也是最小值；t 是当前迭代次数，tmax是最大迭代次数。该方法更好地控制了全局搜索能力和局部搜索能力，加快了收敛速度，提高了算法的性能。然而，由于惯性权重采取的是线性递减策略，一旦在迭代初期搜索不到最好点，那么随着ω的减小，局部搜索能力加强，就极容易陷入局部最优。

为克服这种不足，文献[15]经过大量研究实验，提出了惯性权重的2 种非线性递减策略，计算公式为：

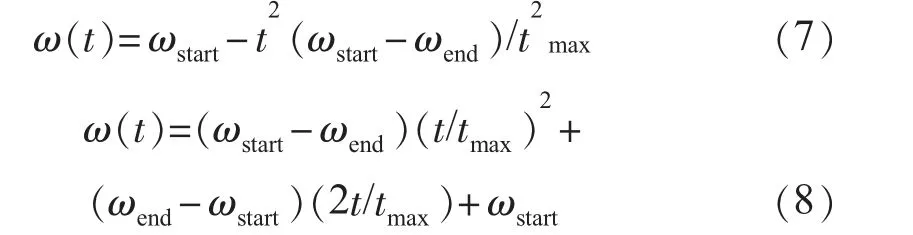
由式（7）、（8）可以看出，在迭代初期，ω的减小趋势缓慢，全局搜索能力很强，有利于找到很好的优化种子。而在迭代后期，ω的减小趋势加快。因此一旦在前期找到合适的种子，上述策略就可以使得算法收敛速度加快，在一定程度上减弱了前述线性递减策略的局限性。

2.2 改进的PSO 算法

在PSO 算法中，每个粒子代表问题的一个解。所有粒子迭代的目的就是为了找到适应值最优的位置。为此每个粒子均通过3个方面进行更新：自身位置；对自己历次位置中择优选取的最佳位置；对所有粒子位置中择优选取的最佳位置。

其中，学习因子c2反映了粒子间的信息交流，对PSO 算法的性能影响较大。理想状态下，一个好的策略应使得算法在搜索初期时，粒子能够遍历整个空间；而在搜索末期，粒子能够避免陷入局部极值。为此，与以往大多数研究中将学习因子c2设定为定值不同，文中将学习因子c2随着迭代次数的变化而变化，并将其与惯性权重的变化相结合，提出了新的PSO 算法策略。

其基本思想是：在搜索初期，粒子飞行主要参考粒子本身的历史信息；在搜索后期，则更加注重社会信息。学习因子c2的计算公式为：

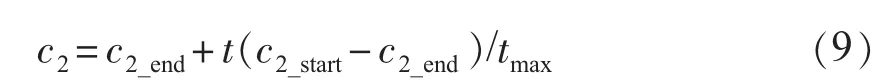
式中：c2_start，c2_end分别为c2的迭代初值和迭代终值。

2.3 改进PSO 算法的实现

2.3.1 初始化粒子

在网架扩展规划的初始种群设置中，倘不加选择，任意选取两节点作为新建线路端点的话，则仅扩建一条输电线路，粒子迭代过程中需遍历的总数将达n（n-1）/2；若扩建2 条输电线路，需遍历的总数将高达n（n-1）（n-2）（n-3）/4。随着扩建输电线路数目的增加，初始种群数目将更多。从简单化角度出发，文中将风电并网点作为新建线路的一个端点，另一端点为一个非常规发电机并网端点。

网架扩展规划是通过在可能的线路走廊上扩建或新建线路来实现的，因此定义：若扩建或新建n 条线路，则其对应的粒子为（x1，x2，K，xn）。其中，元素xi表示在风电并网点与节点xi之间新建一条输电线路。

2.3.2 适应度函数

适应度函数与研究问题的目标函数具有很强的关联性。由于目标函数是关于线路输送功率和节点电压的表达式，而文中研究的是如何通过网架扩展规划来缓解含风电场电力系统的输电阻塞，因此，适应度函数即可由目标函数直接转化而来。

2.3.3 实现步骤

（1）初始化算法。设定PSO 算法的各类参数：搜索空间的上限Ud，下限Ld；学习因子c1，c2；最大迭代次数tmax或收敛精度ξ。随机初始化种群粒子。

（2）评价每一个粒子。依据适应度函数，计算每一个粒子的适应值，并据此选择粒子当前的最优位置和全局最优位置。

（3）更新粒子位置。用式（4）和式（5）对每一个粒子的位置进行更新。

（4）检验是否符合结束条件。如果当前的迭代次数达到了预先设定的最大次数tmax，或最终结果小于预定收敛精度ξ 要求，则停止迭代，输出最优解，否则转到步骤（2）。

3 仿真算例及结果讨论

仿真算例以改进后的IEEE 39 节点系统作为研究对象，详细参数参见文献[16]。该系统含有39个节点和46 条输电线路，如图1 所示。不计平衡节点，该系统总装机规模和负荷水平分别为46.20 p.u.和46.41 p.u.（以100 MV·A为基准功率）。假设风电并网于节点22，风速变量是符合威布尔分布的随机变量。风电场内安装了100 台Vestas V112-3.0 MW 型号的风电机组，其切入、额定和切出风速分别为4 m/s，16 m/s 和25 m/s[17]。

3.1 改进前后的迭代结果比较

为描述方便，定义3.1 节中惯性权重的改进算法依次为ω1，ω2，ω3。将前述的学习因子改进与惯性权重改进进行组合，就可以得到6 种不同的算法：ω1，ω1c2，ω2，ω2c2，ω3，ω3c2。算例对这6 种不同的算法均作了仿真计算，结果如表1 所示。

由表1 可以看出：（1）不同算法下，迭代计算结果都一致，均为（8，18）。这说明在上述算法下，迭代结果未出现陷入局部最优解的问题。这是由于在初始化粒子时，选择了多达5000个的初始粒子。初始粒子数目越多，陷入局部最优解的可能性越小。（2）与仅依靠惯性权重改进算法相比，同时动态优化调整惯性权重和学习因子的改进PSO 算法，不管是在迭代次数还是在迭代时间上，均具有明显的优势。这就说明了文中所提出的改进PSO 算法的优越性。

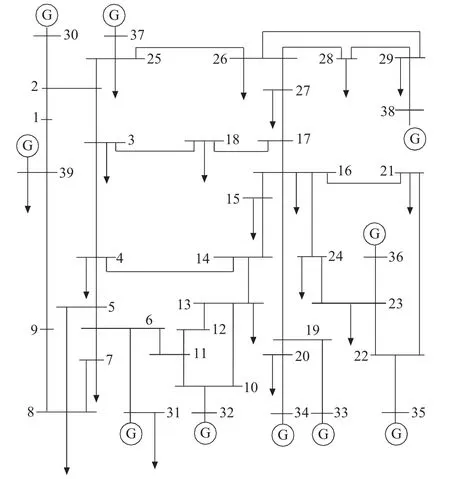
图1 IEEE 39 节点网架结构

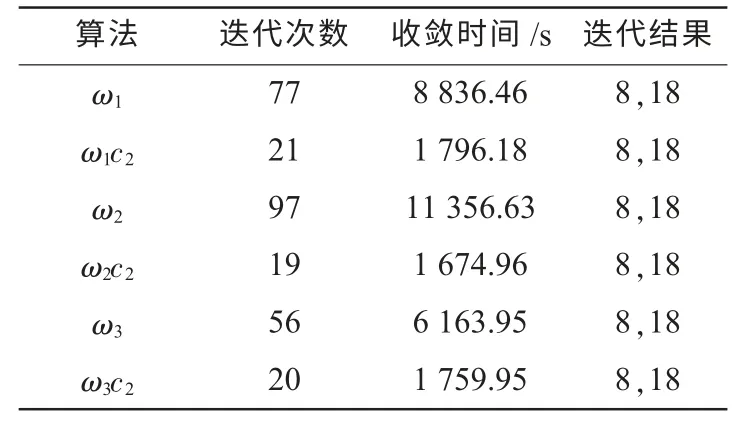
表1 算法改进前后的迭代结果比较

3.2 网架扩展前后的系统输电阻塞程度比较

由上节计算结果可知：当通过扩建2 条线路来缓解含风电场电力系统的输电阻塞时，PSO 优化算法的最终结果为（8，18）。通过基于Gram-Charlier 级数展开的概率潮流计算[18]，文中研究了原先重负荷线路在网架扩建前后输送功率期望值的变化情况，如表2 所示。

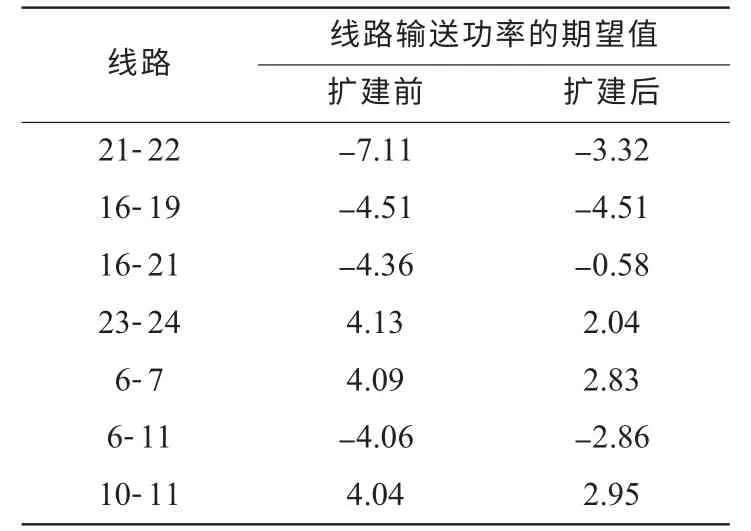
表2 网架扩建前后原重负荷线路输送功率期望值变化

由表2 可以看出：网架扩建前，线路21-22的阻塞程度较为严重；网架扩建后，该线路输送的部分功率被其他轻负荷线路所承担，原先所面临的阻塞压力得到极大缓解。

4 结束语

为缓解风电大规模并网发电后部分线路可能出现的输电阻塞现象，基于改进后的PSO 算法，采用网架扩展规划这一技术手段，对含风电场电力系统的网架规划进行了研究，实现了缓解部分线路输电阻塞的目的。在PSO 算法中，惯性权重决定了粒子先前位置对当前位置的影响，而学习因子则决定了粒子本身经验和群体经验对粒子运动轨迹的影响，反映了粒子间的信息交流。通过合理动态调整这2个参数，有效避免了陷入局部最优解、加快迭代收敛速度，对提高PSO 算法的性能具有重要的意义。

[1]张乐丰，王增平.风电并网对电力系统的影响[J].江苏电机工程，2011，30(2)：81-84.

[2]崔晓丹，李 威，任先成，等.风电并网对电力系统的影响[J].江苏电机工程，2012，31(6)：1-5，10.

[3]刘 健，杨文宇，余健明，等.一种基于改进最小生成树算法的配电网架优化规划[J].中国电机工程学报，2004，24(10)：103-108.

[4]BINATO S,PEREIRA M V F,GRANVILLE S.A New Benders Necomposition Approach to Solve Power Transmission Network Design Problems[J].IEEE Transactions on Power Systems,2001,16(2)：235-240.

[5]BAHIENSE L,OLIVEIRA G C,PEREIRA M,et al.A Mixed Integer Disjunctive Model for Transmission Network Expansion[J].IEEE Transactions on Power Systems,2001,16(3)：560-565.

[6]程浩忠，张 焰.电力网络规划的方法与应用[M].上海：上海科学技术出版社，2002：150-155.

[7]DA SILVA E L,ORTIZ J M A,DE OLIVEIRA G C,et al.Transmission Network Expansion Planning under a Tabu Search Approach[J].IEEE Transactions on Power Systems,200l,16（l）：62-68.

[8]MAGHOULI P,HOSSEINI S H,BUYGI M O,et al.A Multi-objective Framework for Transmission Expansion Planning in Deregulated Environments[J].IEEE Transactions on Power Systems,2009,24(2)：1051-1061.

[9]翟海保，程浩忠，吕干云，等.多阶段输电网络最优规划的并行蚁群算法[J].电力系统自动化，2004，28(20)：37-42.

[10]BRAGA A S,SARAIVA J T.Transmission Expansion Planning and Long Term Marginal Prices Calculation using Simulated Annealing [C]//Power Tech Conference Proceedings,Bologna,2003：7-9.

[11]王靖然，余贻鑫，曾 沅.离散猴群算法及其在输电网扩展规划中的应用[J].天津大学学报，2010，43(9)：798-803.

[12]王赛一，王成山.遗传禁忌混合算法及其在电网规划中的应用[J].电力系统自动化，2004，28(20)：43-46，62.

[13]SHI Y,EBERHART R.A Modified Particle Swarm Optimizer[C]// IEEE International Conference on Evolutionary Computation Proceedings,Anchorage,1998：69-73.

[14]SHI Y,EBERHART R C.Empirical Study of Particle Swarm Optimization[C]//Proceeding of Congress on Evolutionary Computation，Piscataway,New Jersey,1999：1945-1949.

[15]陈贵敏，贾建援，韩 琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报，2006，40(1)：53-56，61.

[16]PAI M A.Energy Function Analysis for Power System Stability Analysis by the Direct Method of Lyapunov[M].Boston:Kluwer Academic Pub,1981：339-345.

[17]Turbine overview[EB/OL].http://www.vestas.com/en/wind-power-plants/procurement/turbine-overview.Aspx#/vestas-univers.

[18]ZHANG P,Lee S T.Probabilistic Load Flow Computation Using the Method of Combined Cumulants and Gram-charlier Expansion[J].IEEE Transactions on Power Systems,2004,19(1)：676-682.