以风险为基础调查或监测证明无疫的样本量与敏感性计算

沈朝建，刘丽蓉，康京丽，王幼明，李 印，刘爱玲，黄保续

（中国动物卫生与流行病学中心，山东 青岛 266032）

以风险为基础的调查或监测作为一种用于早期发现动物疫病或证明无疫的一种方法，由于可以节约成本，而一直深受大家关注。近年来，由于该方法内在偏倚引起的不能估算其置信水平，一直困扰着流行病学研究人员和动物疫病管理人员如何实施这个有效但不能定量分析其效果的调查或监测。过去10年里，流行病学专家们研究了许多与以风险为基础监测有关的分析性问题，能够定量分析其系统的敏感性和置信水平[1-4]。但如何正确的应用一些概念和以风险为基础抽样一直是我们所面临的挑战。本文目的是以一种简单的、引导性的方式说明以风险为基础的抽样证明无疫的理念和方法。

1 以风险为基础的调查或监测与代表性抽样证明无疫基本原理回顾

1.1 以风险为基础的调查或监测含义与作用 以风险为基础的调查或监测是指有意识地抽取更可能感染或感染时更容易产生阳性检测结果的抽样单元（动物个体或群），是“故意”使调查或监测产生偏倚，主要用动物群体中的无疫证明或发现疫病。通过优先抽取高风险亚群，抽取更少的单元就可以获得同代表性抽样相同的无疫的把握。如国际上关于疯牛病的监测即为以风险为基础的监测，根据不同类型的牛检测疯牛病阳性的可能性不同，即不同类型的牛所在亚群群内流行率不同，将检测对象分为四类，临床疑似牛、紧急屠宰牛、死牛和常规屠宰牛，其中以临床疑似牛检出BSE阳性的可能性最大，同时将不同类的牛按年龄进行进一步细分，以4～6岁的牛检出BSE阳性的可能性最大[5]。从中可以看出，以风险为基础的调查或监测需要清楚的掌握疫病相关风险因素，以便提高发现疫病或感染的可能性；如果对疫病特征知之甚少或不掌握相应的风险因素，不可能开展以风险为基础的抽样；与代表性抽样相比，以风险为基础的调查或监测对于发现疫病而言更有效。但是，对于以风险为基础的调查或监测，应该确保对每一个亚群的抽样能够代表本亚群，且代表性抽样是以风险为基础抽样的基础。

1.2 群敏感性及其意义 动物流行病学研究中的群敏感性（Herd Sensitivity，HSe）是指感染或发病群产生阳性的群检测结果的概率[6]。从另一个角度理解，即当群未感染或疫病不存在时，证明无疫或发现疫病的把握。对于特定群，如果只要发现1只动物感染即认为该群感染，那么群敏感性表示为：

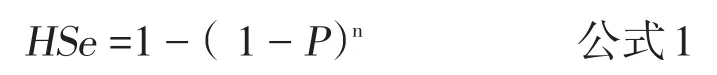
其中，Hse为群敏感性，p为群内流行率，n为检测动物数。

上述是所用试验为“完美”试验条件下的计算公式。如果试验存在偏差，那么以试验检测阳性为感染或发病的条件下，群敏感性表示为：

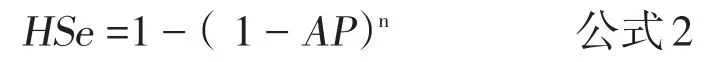
其中，AP为表观流行率，即根据试验结果直接计算获得的流行率，是试验阳性结果数和检测动物总数的比例[7]，表示为：

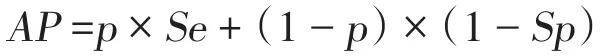
根据群敏感性和表观流行率公式，可以看出影响群敏感性的因素包括所用试验的敏感性（Se）和特异性（Sp）、群内流行率（p）、检测时抽取的样本量（n），以及判断群是否感染的阈值。动物疫病实践中，筛检阳性的动物会用诊断试验进行确诊，这种策略为多重试验的垂直策略，其特异性会大幅升高，所以假定试验的特异性为1，那么群敏感性表示为：

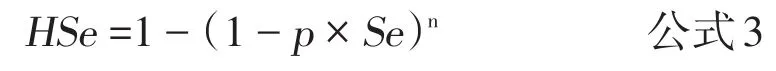
对公式1和公式3进行反推，即可得到

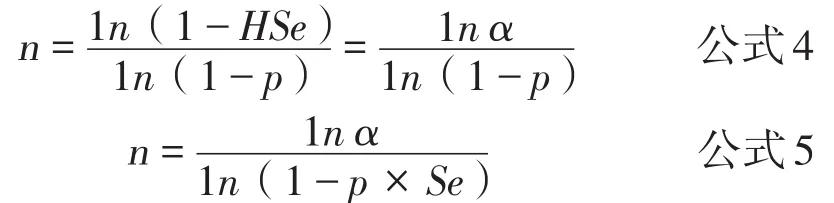
公式4为群体较大且群内个体数对样本量无影响时，证明无疫的样本量计算公式，其中α为可接受误差，即允许犯错误的可能性，p为预定流行率。公式5是考虑检测方法敏感性Se条件下，抽样数量的计算公式[8]。

1.3 证明无疫或发现疫病的代表性抽样样本量计算 当所调查目标群内个体数量较少时，证明无疫或发现疫病的样本量计算公式为：

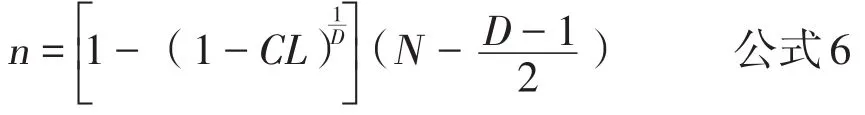
其中n为抽样个数，CL为置信水平，D为群中的阳性动物数（等于群内个体数与预定流行率的乘积），N为群内个体数。

在动物疫病防控实践中，证明无疫或发现疫病通常是通过实验室检测实现的，采用实验室检测就应该考试检测方法的敏感性，即检测到阳性动物。考虑检测试验敏感性的计算公式[9]为：

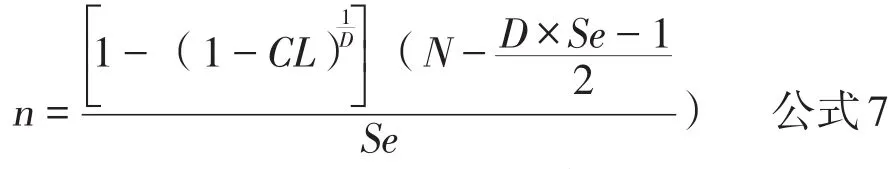
其中Se为检测方法的敏感性，其余参数同公式6。

公式6和公式7不但适用于目标群内个体数量较小的情况，同样适用于个体数量较大，可看做“无限”群证明无疫的样本量计算。当前大多数兽医流行病学抽样软件证明无疫或发现疫病的抽样样本量计算均采用这两个公式。

2 以风险为基础的调查或监测证明无疫样本量计算与敏感性计算

2.1 以风险为基础的调查或监测证明无疫的样本量计算 以风险为基础的抽样，过程和代表性调查抽样一样，但考虑到需要优先抽取高风险单元，因此，抽样过程中的预定流行率、样本大小、系统敏感性均需要校正。为了达到此目的，需要获得两个额外的参数，即不同亚群间的相对风险及其在目标群中所占的比例。为便于理解，本部分以某地奶牛布病为例统一说明以风险为基础证明无疫的调查或监测的样本量计算。

（1）校正不同亚群的疫病风险：考虑到不同亚群感染风险不同，为了不会人为的改变预定流行率，用下述公式校正相对风险值：

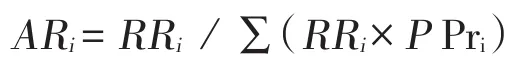
其中ARi为各个亚群校正的风险值；

RRi为相对风险值；

PPri为各亚群在源群中所占比例。

∑（RRi×PPri）为每一个风险群相对风险与群所占比例乘机之和。这样对于每一个风险群均可产生一个校正的风险估计值，用这个风险估计值乘以预定流行率，可以得到这个群校正后的感染概率。例如，根据研究结果或已有的资料分析，认为大规模场的感染风险（RR=3）是小群的3倍（RR=1），大规模场占整群的10%，那么大规模场校正的风险为3/（3×0.1+0.9）=2.5，小规模场校正的风险为1/（3×0.1+0.9）=0.833。

（2）计算各风险群预定流行率：风险群i预定流行率Pi*计算公式：

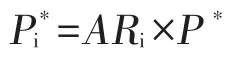
其中ARi为风险群i校正的风险值，P*为总预定流行率。

继续前面例题，如果预定流行率为0.02，那么大规模场校正的感染概率（流行率）为0.05，小规模场校正的感染概率（流行率）为0.017。所有计算的关键是保持群的总预定流行率不变（0.05×0.1+0.017× 0.9=0.02），因此，为了达到此目的，需要在不同风险群中重新分配预定流行率。

（3）样本量计算：对于以风险为基础的抽样，在确定样本中不同风险群的比例后，需要用加权后的预定流行率P*a代替P*，表示如下：

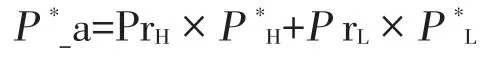
其中

PrH为样本中高风险单元所占比例

PrL为样本中低风险单元所占比例

P*H为修正后的高风险单元感染的概率

P*L为修正后的低风险单元感染的概率

所以，以风险为基础的抽样公式为：

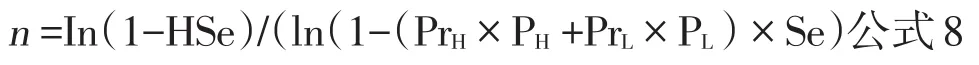
可以看出，计算以风险为基础的抽样样本量，首先需要确定样本中高风险单元和低风险单元各自所占的比例，以及高风险单元和低风险单元各自修正的流行率。继续之前的例子，如果计划样本中高风险群的比例为60%，低风险群为40%，所用检测试验的敏感性为80%，为了保证调查或监测系统的敏感性为95%，需要检测多少个群？根据公式8：

可以看出，需要抽取101个样本，其中61个高风险群，40个低风险群。如果采用代表性抽样，将数据带入公式5计算得出需要抽取186个群，明显高于以风险为基础的抽样。如果群内抽样也采取以风险为基础的策略，可以使用上述相同的过程来确定每个群中的抽样数量。

上述为无限群证明无疫的抽样，如果目标群为“有限”群，即数量较少，求出加权修正的预定流行率后，带入代表性证明无疫样本量计算公式6或公式7计算出抽样数量，然后再在高风险群和低风险群之间分配。

2.2 以风险为基础调查或监测证明无疫的敏感性计算 前述公式3也可以用来计算调查活动或监测系统的敏感性，即用群敏感性HSe代替试验的敏感性Se、群预定流行率和抽样群数代替动物个体水平的预定流行率和动物数。如果每个单元的敏感性和感染概率（预定流行率）不同，可以用下述公式计算群敏感性或系统敏感性：

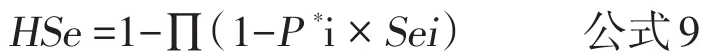
注：这里与前述一样，由于多数情况是为了证明无疫或发现疫病，筛检阳性后会进行进一步的确诊，这样可以有效排除假阳性，因此，试验过程的特异性很高，假定为1。

为将不同的感染风险引入到计算公式中来，所要做的是将每个单元相应修正过的感染概率列入到公式中来。继续前述的例子，为证明某地区奶牛群不存在布病，采用对每个群的散装奶进行检测的方式，对该地区奶牛群进行调查。假定试验的敏感性为80%，该地区大规模奶牛场（群）布病感染的相对风险为3，且10%的奶牛场（群）为大规模场。我们共抽取了55个大规模奶牛场（群）和45个小规模奶牛场（群）进行检测。那么在预定流行率为2%，且所有检测为阴性的条件下，系统敏感性是多少？根据公式9，系统敏感性（P*H为高风险群的流行率，P*L为低风险群的流行率）

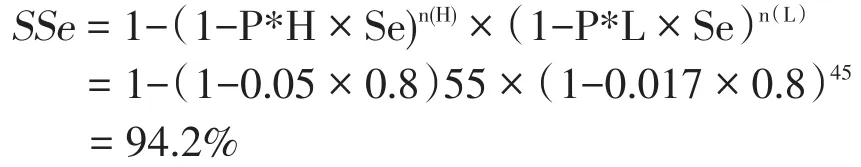
对于代表性抽样而言，在抽取相同样本量的情况下，系统敏感性=1-(1-0.8×0.02)100=80.1%。也就是说，如果该地区存在奶牛布病的情况下，采用以风险为基础的抽样，有94.2%的把握发现它，而采用代表性抽样，只有80.1%把握发现它。

3 讨论

本文对以风险为基础的调查或监测证明无疫或发现疫病的基本原理以一种简单、直观的方式做了简要介绍，推导出了以风险为基础的抽样样本量计算和结果的敏感性分析，并举例予以说明。从中可以看出，同代表性抽样证明无疫的样本量计算相比，在保证证明无疫的把握不变的条件下，以风险为基础的抽样样本量计算具有一定的灵活性，即在保证对目标群所设定的预定流行率不变的情况下，可以通过调整样本中不同风险群所占比例来调整样本量，从而达到节省资源的目的。此是以风险为基础抽样广受关注的关键，亦是其魅力所在。

[1]Hadorn D C，Hauser R，Katharina D C，et al.Risk-based design of repeated surveys for the documentation of freedom from nonhighly contagious diseases[J].Prev VetMed,2002.56(3)：179-192.

[2]Martin P A，Camerom A R，Barfod K，et al.Demonstrating free⁃dom from disease using multiple complex data sources 2：case study-classical swine fever in Denmark[J].Prev Vet Med，2007，79(2-4)：98-115.

[3]Martin PA，Cameron A R，Greiner M.Demonstrating freedom from disease usingmultiple complex data sources 1：a new methodology based on scenario trees[J].Prev VetMed，2007，79(2-4)：71-97.

[4]Gustafson L，KLotins S，Cameron A，et al.Combining surveil⁃lance and expert evidence of viral hemorrhagic septicemia free⁃dom：a decision science approach[J].Prev Vet Med，2010，94(1-2)：140-153.

[5]OIE.OIE Terrestrial Animal Health Code(volume I)[M].21th Edi⁃tion Paris：OIE，2012.

[6]Christensen，JIGardner A.Herd-level interpretation of test results for epidemiologic studies of animal diseases[J].Prev Vet Med，2000，45(1-2)：83-106.

[7]Dohoo IM，Stryhn H.Veterinary Epidemiologic Research[M].21th Edition Charlottetown VER Inc，2010.

[8]Thomas F B.Some practical considerations in sampling livestock populations to estimate disease prevalence and other parameters[J].Prev VetMed，1984，2(1-2)：450-462.

[9]Cannon R M.Sense and sensitivity--designing surveys based on an imperfect test[J].Prev VetMed，2001，49(3-4)：141-146.