多活性中心催化剂催化丙烯聚合的均匀球Monte-Carlo模型

洪东峰，隋述会，吴文辉*

（1. 北京理工大学材料学院，北京市 100081；2. 中科合成油技术有限公司，北京市 101407）

目前，约90%的聚丙烯（PP）采用Ziegler-Natta（Z-N）催化剂合成[1]。人们通过优化聚合工艺参数使催化剂性能尽可能发挥，从而提高PP性能。PP生产中，在催化剂作用下，丙烯以催化剂颗粒为核心参与聚合，从最初的10～200 μm的小粒径催化剂核心逐渐生长为粒径1 000～5 000 μm的PP颗粒[2-3]。MgCl2负载型多活性中心Z-N（MgCl2-Z-N）催化剂的催化动力学十分复杂，在丙烯聚合过程中起支配作用，同时丙烯在催化剂颗粒中的扩散也具有重要作用[4]。催化机理模型通常分为化学模型（动力学控制）和物理模型（扩散控制）。化学模型得益于数学的不断发展，如连续变量逼近法、矩阵法、Galerkin h-p有限元法等，近年来Monte-Carlo方法的应用越来越多，且更注重利用微分方程研究催化动力学[5]，甚至开发了动态Monte-Carlo模型，描述聚合时间对聚烯烃链长分布的影响[6]，但这些方法通常不考虑聚合过程中的传质和/或传热[6-7]。物理模型主要考虑聚合过程中的传质和/或传热等扩散作用[3,8]，扩散理论认为：在径向上，催化剂裂片分布在不同浓度的单体和链转移剂（主要是H2）中，得到的聚合物链段基本相同，但由于空间位阻效应而形成不同的立构分布。物理模型的应用并不普遍。事实上，丙烯聚合过程中的化学作用和物理作用是同时存在的，且两者相互影响，Sun Jianzhong等[8-9]利用多层模型对以上因素进行了研究，使丙烯聚合催化模型的建立较之前有很大进步。研究表明，Z-N催化剂在MgCl2上的负载并非呈层状，而是均匀分布[5]，因此，多层模型与MgCl2-Z-N催化剂的催化过程尚有不同。

本研究应用Monte-Carlo方法对丙烯聚合均匀球模型进行积分处理，建立均匀球Monte-Carlo模型（UBMCM）。采用中国石油化工股份有限公司开发的第四代多活性中心催化剂DQ-Ⅲ，实验数据来自工业PP环管装置。

1 模型建立

Zacca等[2]首先提出Z-N催化剂的动力学机理：不同氧化态的Ti具有不同的催化性能，从而使催化剂具有多种活性中心。通过解析PP的凝胶渗透色谱（GPC）曲线，确定DQ-Ⅲ催化剂具有5个活性中心，决定系数为0.999 98，决定系数越接近1，解析结果（见图1）越可靠。

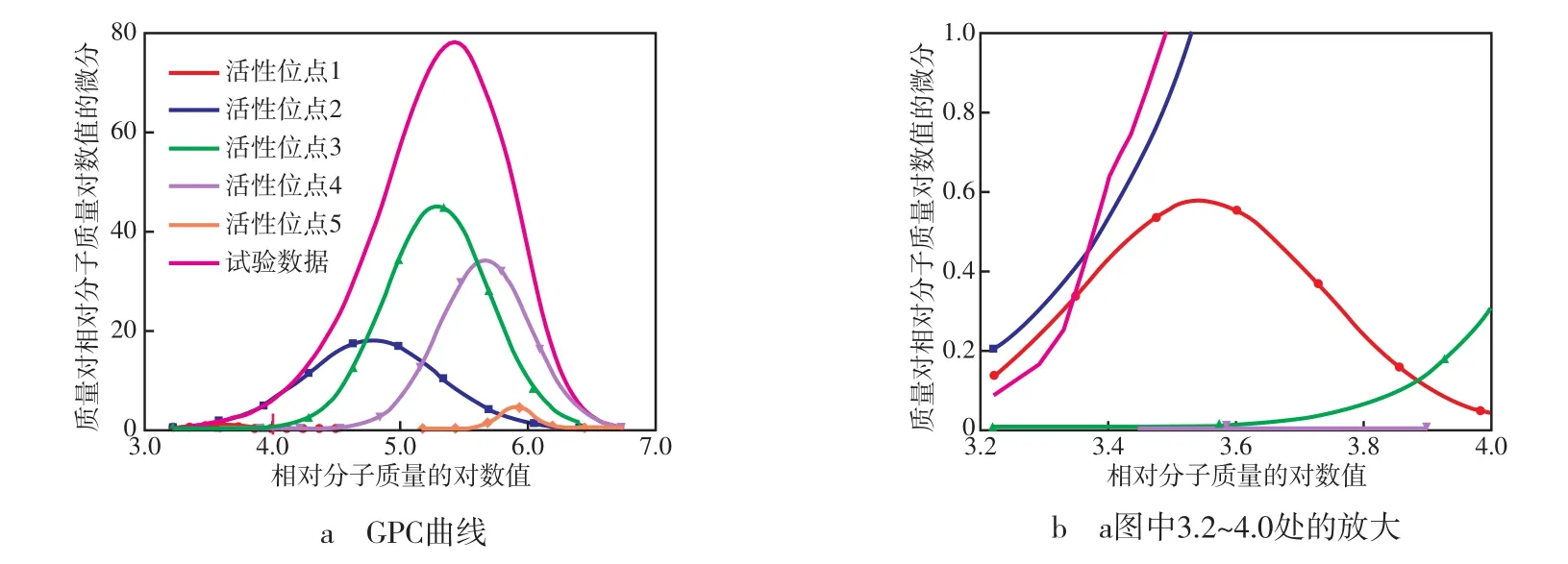
图1 DQ-Ⅲ催化剂的活性中心解析结果Fig.1 Analytical results of the active sites in DQ-Ⅲ catalyst

针对第四代MgCl2-Z-N催化剂引发的丙烯聚合，提出以下假设[2-3]：1）活性中心在催化剂内的分布，以及单体、催化剂、H2等在反应器内的分布均匀；2）加入反应器中的催化剂颗粒粒径相同；3）催化剂和/或PP颗粒内/间的热交换可以忽略；4）聚合初期，催化剂颗粒的破裂在瞬间完成。

聚合初始阶段，催化剂破裂成若干小颗粒且能保持球形，丙烯单体通过扩散进入催化剂内部与活性中心接触并发生反应，聚合过程中，催化剂作为丙烯聚合的模板和微反应器，以催化剂为核心，经历链引发、链增长和链转移，得到一个PP颗粒[9]。催化动力学模型由活性中心活化、链引发、链增长、链转移、活性中心转移、活性中心失活等6个过程及每个过程的速率常数来描述。

UBMCM中，丙烯分子透过催化剂外壳，在扩散作用下进入催化剂内部，遵循Fick扩散定律。丙烯单体在催化剂颗粒中的扩散见图2。

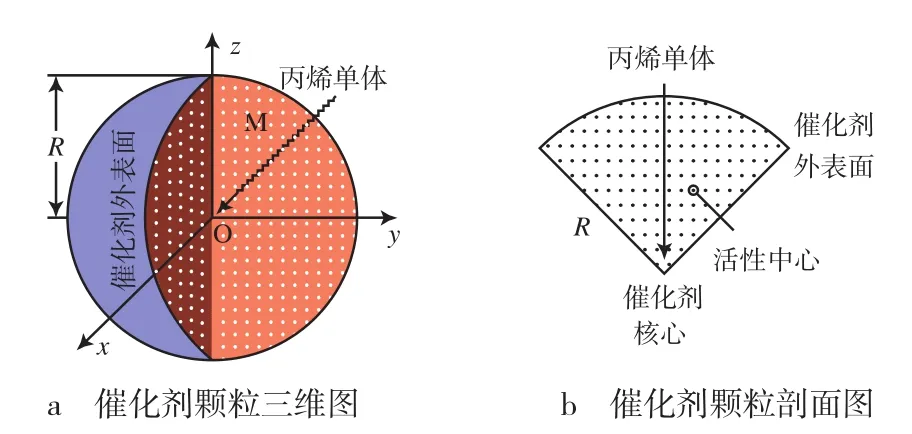
图2 丙烯单体在催化剂颗粒中的扩散Fig.2 Diffusion of the propylene monomer in catalyst particles

丙烯的浓度梯度计算见式（1）～式（2）。

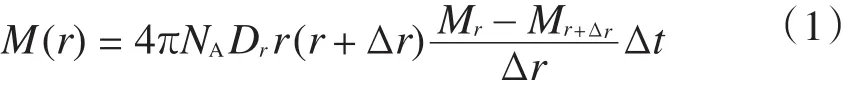
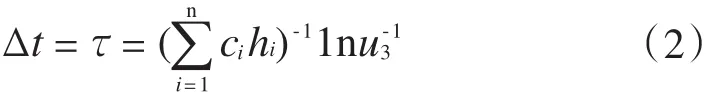
式中：M（r）表示丙烯的浓度梯度；NA是Avogadro常数；Dr是r处的扩散系数，r是活性中心与球心间的距离；Δr为半径的变量，Δr＜0；Mr和Mr+Δr分别是r和r+Δr处的丙烯浓度；τ和Δt是设定的时间间隔；ci是stochastic速率常数；hi是参与第i种基元反应的分子数；n是总基元反应数；u3是随机数。

单体丙烯自催化剂外向其核心扩散，当扩散至[r, r+Δr]时，催化剂颗粒的体积按式（3）计算。

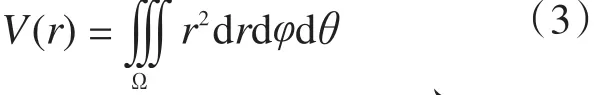
半径的积分区间是[r, r+Δr]，φ和θ的积分区间均为[0, 2π]，用式（4）～式（6）表述。

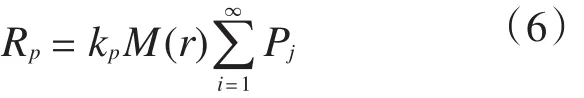
式中：kp是聚合反应速率常数；Pj是第j种反应的几率；Rp是聚合反应速率；ρp是催化剂/PP复合颗粒的密度；Mw是PP的相对分子质量；Vr，Vr+Δr分别是时间（t）和t+Δt时复合颗粒的体积。

随着聚合的进行，催化剂/PP颗粒的半径和体积逐渐增加，但其密度保持不变，故半径或体积的增加与参加反应的丙烯量有关。

UBMCM的算法流程见图3。计算在Matlab 2012b软件上进行。

2 结果与讨论

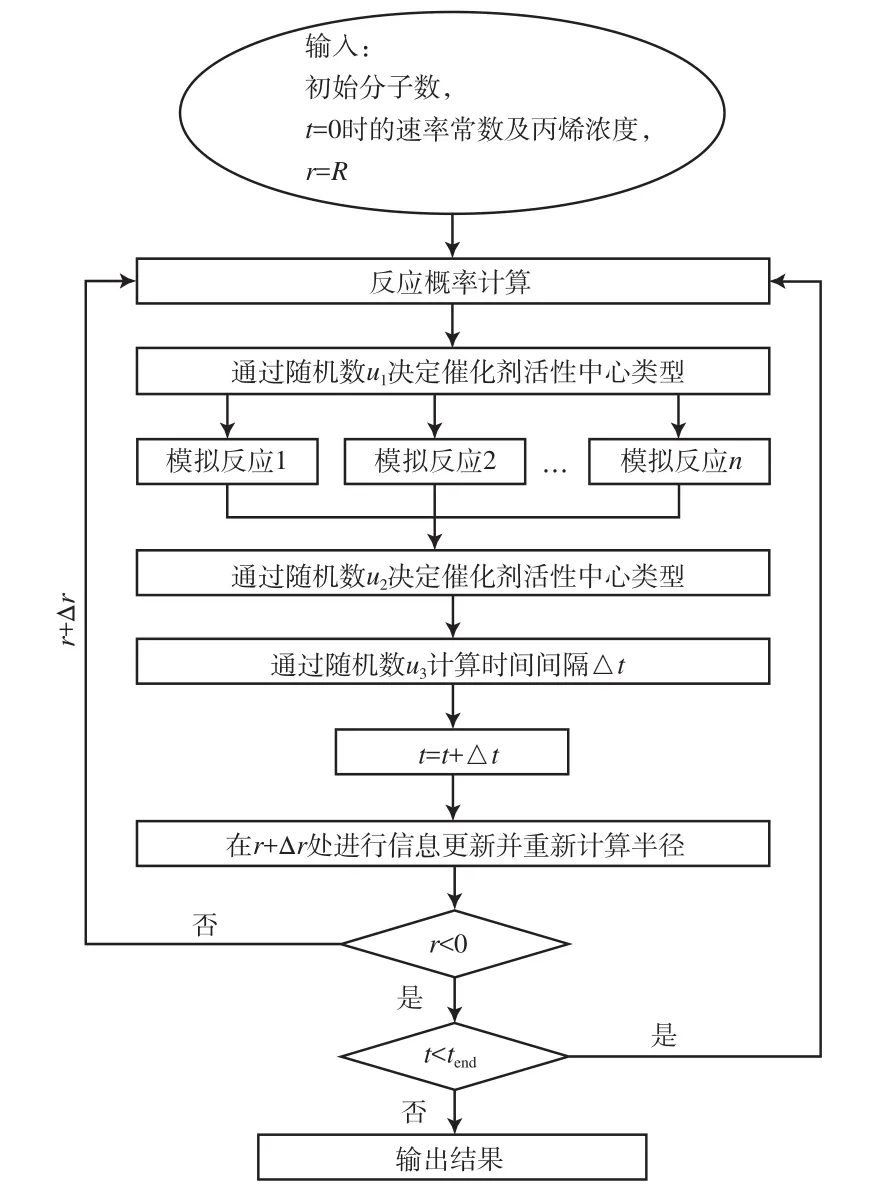
图3 UBMCM的算法流程Fig.3 Algorithm flowchart of the UBMCM model

采用UBMCM模拟丙烯聚合的反应动力学，温度为70 ℃，分析了DQ-Ⅲ催化剂的活性，PP的Mw、相对分子质量分布（Mw/Mn）和粒径分布，并与Zacca等[2,10]使用的Monte-Carlo模型（MCM）和Wang Wei等[9]使用的多层Monte-Carlo模型（MLMCM） 的模拟结果进行比较。

2.1 催化剂活性

用UBMCM模拟多活性中心Z-N催化剂催化丙烯聚合时，预测结果与实验结果间的相关系数为0.994 1，而用MCM和MLMCM时的相关系数分别为0.992 3和0.992 5[2,9]。3种模型中，UBMCM曲线与实验点吻合最好，说明UBMCM对该现象的描述较好。这是因为随着聚合的进行，催化剂颗粒内部的单体浓度梯度变小，Fick扩散的动力降低。用UBMCM预测的结果与实验值吻合度高于用MCM和MLMCM，是因为UBMCM考虑了扩散对丙烯聚合的影响，模型更精确。从图4可以看出：聚合前期，扩散阻力对聚合不利，而后期有利于聚合，聚合过程可分为3个阶段。第一阶段（0～1.0 h）为扩散控制，由于扩散阻力，催化剂内部及活性中心周围单体较少，催化剂浓度低，扩散过程非常缓慢，且占主导地位，催化剂活性较低，但随着单体向催化剂内部扩散，催化剂颗粒内丙烯浓度增加，催化剂活性增加较快（曲线斜率大）。第二阶段（1.0～4.0 h）为反应控制，单体开始在催化剂活性中心周围积累，单体浓度增加，同时扩散逐渐趋于平衡，催化剂活性增加趋势减缓（曲线斜率减小）。第三阶段（4.0～6.0 h）为稳态阶段，由于失活反应，故单体和活性中心的浓度均降低，催化剂活性不再有明显变化。

图4 多活性中心催化剂活性与聚合时间的关系Fig.4 Relationship between the multi-active-site catalyst and the polymerization time

2.2 PP的Mw

从图5可以看出：相对于MCM与MLMCM，用UBMCM模拟时由于考虑了扩散的影响，对Mw的预测值与实验值吻合度更高，对丙烯聚合的描述更精确。随着聚合的进行，Mw逐渐增加，直至接近最大值，其中，用UBMCM的预测曲线比用MLMCM的平滑。

图5 PP的Mw与聚合时间的关系Fig.5 Relationship between the relative molecular mass of PP and the polymerization time

2.3 PP的Mw/Mn

从图6可以看出：对于多活性中心催化剂引发丙烯聚合，聚合3.5～4.0 h时，PP的Mw/Mn逐渐趋于恒定，约为4.4。造成Mw/Mn变宽的原因有两个：催化剂的多活性中心性质和扩散作用。聚合过程中，活性中心由Ti3+转换成Ti2+，Ti2+与丙烯之间的反应不活跃是造成PP的Mw/Mn变宽或其曲线出现双峰的主要原因。用UBMCM预测的Mw/Mn与工业或实验数据的吻合度最高，MLMCM次之，MCM最低，因此，UBMCM在精确模拟丙烯聚合和预测产品性能方面有优势。

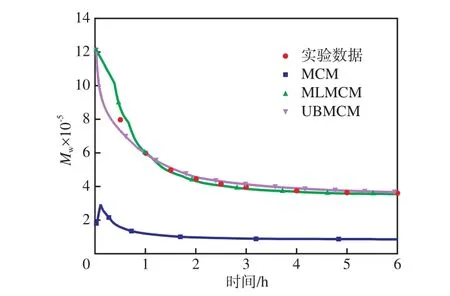
图6 PP的Mw/Mn与聚合时间的关系Fig.6 Relationship between Mw/Mn of PP and the polymerization time

2.4 PP的粒径

聚合过程中，单/多活性中心催化剂催化生成的PP的粒径变化趋势基本相同。从图7看出：扩散控制阶段，即第一阶段，催化剂活性中心周围的单体浓度低，PP粒径增速较慢；反应控制阶段，即第二阶段，在第一阶段单体浓度梯度作用下，催化剂内部单体浓度增加，PP粒径增速较快；稳态阶段，即第三阶段，PP粒径增速减小并趋于稳定。

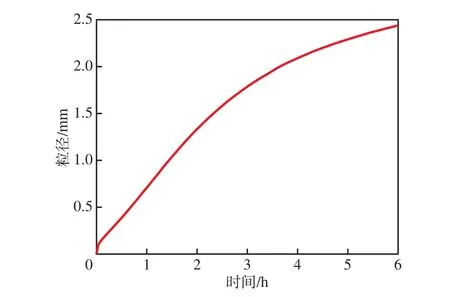
图7 PP粒径与聚合时间的关系Fig.7 Relationship between the particle size of PP and the polymerization time

3 结论

a）根据UBMCM模拟结果，聚合反应动力学和颗粒间/内的扩散效应对催化剂的催化性能和PP性能均有重要影响。

b）丙烯聚合过程可分为扩散控制、反应控制和稳态3个阶段。

c）UBMCM考虑到扩散阻力，对多活性中心催化剂催化丙烯均聚合过程的描述更精确，对PP性能的预测更准确。

[1] Zhang Hexin, Lee Y-J, Park J-R, et al. Control of molecular weight distribution for polypropylene obtained by a commercial Ziegler-Natta catalyst: effect of a cocatalyst and hydrogen[J].Journal of Applied Polymer Science, 2011, 120（1）: 101-108.

[2] Zacca J J, Debling J A, Ray W H. Reactor residence time distribution effects on the multistage polymerization of olefins—I. Basic principles and illustrative examples, polypropylene[J].Chemical Engineering Science, 1996, 51（21）: 4859-4886.

[3] McKenna T F, Soares J B P. Single particle modelling for olefin polymerization on supported catalysts: a review and proposals for future developments[J]. Chemical Engineering Science, 2001,56（13）: 3931-3949.

[4] Cifra P, Bleha T. Stretching of self-interacting wormlike macromolecules[J]. Polymer, 2007, 48（8）: 2444-2452.

[5] Jiang Xue, Wang Hang, Tian Xiuzhi, et al. Effects of doping LiCl into MgCl2-supported Ziegler-Natta catalyst on the molecular weight distribution and isotacticity of polypropylene[J].Industrial & Engineering Chemistry Research, 2011, 50（1）:259-266.

[6] Simon L C, Soares J B P. Monte Carlo simulation of long-chain branched polyolefins made with dual catalysts: a classification of chain structures in topological branching families[J]. Industrial &Engineering Chemistry Research, 2005, 44（8）: 2461-2468.

[7] Luo Zhenghong, Wang Wei, Su Peilin. Modeling of the propylene polymerization catalyzed by single-/multi-active site catalyst: a Monte Carlo study[J]. Journal of Applied Polymer Science, 2008, 110（6）: 3360-3367.

[8] Sun Jianzhong, Eberstein C, Reichert K H. Particle growth modeling of gas phase polymerization of butadiene[J]. Journal of Applied Polymer Science, 1997, 64（2）: 203-212.

[9] Wang Wei, Zheng Zuwei, Luo Zhenghong. Coupled-singleparticle and Monte Carlo model for propylene polymerization[J].Journal of Applied Polymer Science, 2011, 119（1）: 352-362.

[10] Di Drusco G, Rinaldi R. Polypropylene-process selection criteria[J]. Hydrocarbon Process, 1984, 63（11）: 113-117.