基于最优导频的自适应Kalman滤波信道估计方法

张士杰，岳珍梅，李艳红

(1.河南科技大学信息工程学院，河南洛阳471023;2.中国人民解放军91292部队，河北保定074000;3.许昌职业技术学院信息工程系，河南许昌461000)

近年来，超宽带(UWB)无线通信技术和正交频分复用(OFDM)技术相结合的UWB－OFDM技术成为无线通信领域的研究热点，其兼具UWB技术传输速率高、空间容量大、成本低、低功耗的优点和OFDM技术对多径衰落的鲁棒性、频谱利用率高的优势［1－2］。然而UWB－OFDM技术仍然存在一些缺陷，UWB－OFDM系统性能的分析大多是利用时不变S－V室内信道模型，而当UWB信道发生变化时，就不得不考虑子载波间干扰和信道未知因素产生的模型摄动对系统性能的影响［3］。

在时变信道环境中，Kalman信道估计算法是一种广泛使用的算法。文献［4］在MB OFDM系统中，分析对比了基于导频模式的最小二乘(LS)估计、最小均方估计(LMMSE)和Kalman滤波(KF)算法在系统中的性能，其中KF算法表现出良好的信道估计性能，但是这种算法的有效性建立在各种信道参数已知的前提下。文献［5］提出一种扩展的Kalman滤波的信道估计方法，该方法在信道状态参数未知的情况下利用导频跟踪信道变化，但是这种方法忽略了系统噪声和系统模型本身存在摄动对估计性能的影响，甚至这种不良影响会导致滤波发散。文献［6］提出了一种修正的Kalman滤波算法，这种方法能够有效地跟踪信道时变特性和状态转移系数，但是信道在一个符号周期内是时变的，估计器需要进行大量的迭代运算，计算复杂度高，不利于实现。基于上述情况文献［7］提出了一种渐消卡尔曼滤波算法，利用导频的LS估计确定信道初始值和信道转移系数，创新性地引进了衰减因子，从而增大系统噪声方差和观测噪声方差的权值，减小旧数据对滤波的作用，抑制发散的产生。但是该方法未考虑信道时变时子载波间的干扰(ICI)问题。由于ICI的影响，导频LS估计会使初始估计信息的准确性降低，影响信道估计精确性。同时这种方法是在牺牲了系统估计精度的前提下保证了系统的收敛性。文献［8］提出一种数据调制的方法，在发送端将一对极性相反的数据对调制到两个相邻的子载波上进行传输，在接收端通过合并“自动地”消除ICI。

本文根据文献［8］符号调制ICI自消除原理和KF算法，提出了一种基于最优导频的抑制ICI和KF滤波发散的自适应算法。首先根据ICI 自消除原理将一组特殊导频符号调制到相邻子载波上，接收端得到的导频符号通过合并，初步实现ICI自消除的目的;然后在时域上进行Kalman自适应滤波算法，最终求得整个时变信道的信息。

1 UWB－OFDM系统模型

典型的 UWB－OFDM 系统模型［9－10］如图1 所示。

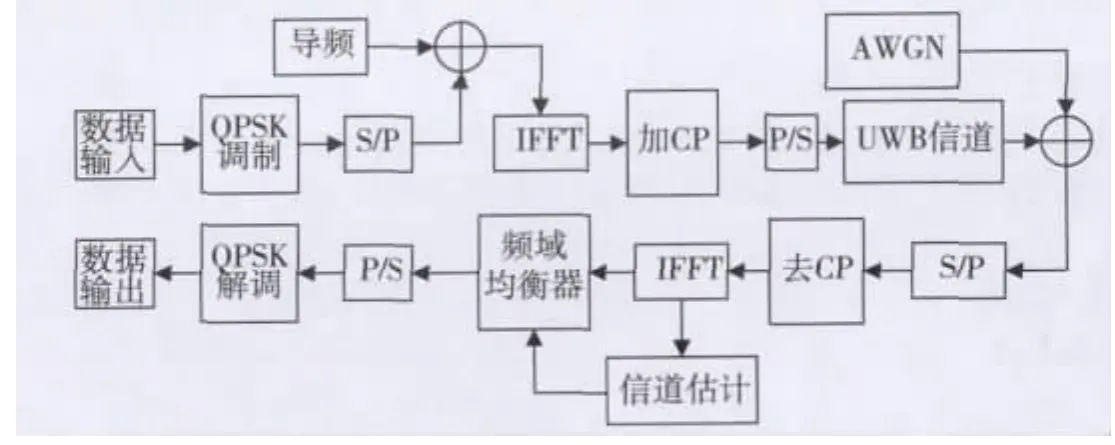
图1 UWB－PFDM系统原理框图

在发送端数据符号通过调制、串并变换和快速傅里叶变换(IFFT)，由频域数据X(i，k)转换为时域信号x(i，n)。则第i个符号周期的OFDM－UWB信号可表示为

式中:0≤n≤N;0≤i≤NOFDM;N为子载波个数;NOFDM为OFDM符号数。

变换之后的数据再经过加入循环前缀(CP)，通过衰落信道送到接收端，接收端则进行与发送端相反的处理过程，最终得到

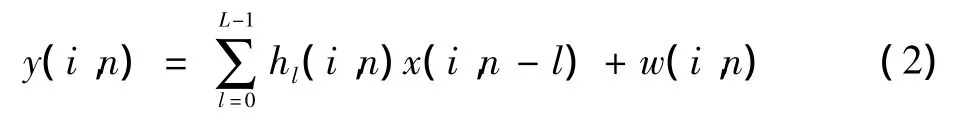
式中:L表示信道路径数;hl(i，n)表示信道冲激响应;w(i，n)是方差为的零均值复高斯过程。则接收时域信号经过快速傅里叶变换(FFT)后得到频域接收信号为

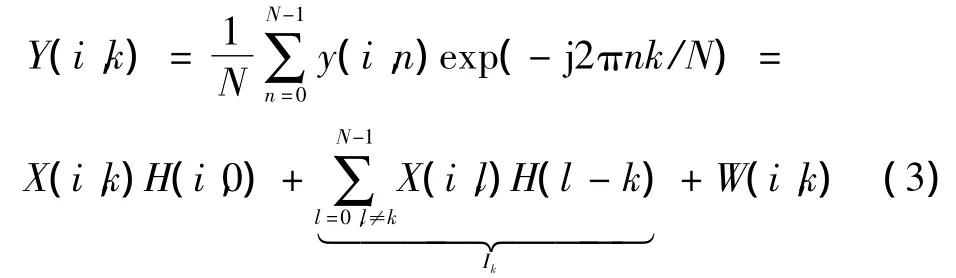
超宽带信道可以用一个有限阶的AR过程来建模，信道频响的动态变化用P阶AR模型可以描述为

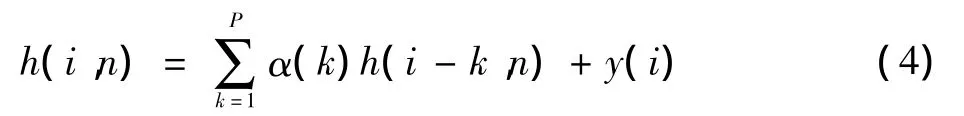
式中:v(i)是方差为的零均值复高斯过程;α(k)表示信道状态转移系数，它由多普勒频偏fdTs决定，为方便讨论，本文采用一阶AR模型。由Yule－Walker方程可得到状态转移系数α=(2πfdTs)和方差，J0表示一阶Bessel函数，fd是多普勒频移，Ts是信息符号周期。

2 基于导频的Kalman信道估计

2.1 最优导频设计

KF初始信息往往是未知的，然而初始信道信息的准确性影响了整个系统估计的性能;当初始信息不准确时，很可能会导致信道滤波发散现象。利用导频进行滤波初始信息的估计是个有效的手段，但时变信道中存在的噪声干扰和ICI严重影响了导频估计的准确性。假设初始信道信息h0未知，信道噪声为初始信息已知的复加性高斯白噪声，但噪声的统计模型因为信道的时变性存在偏差。

首先讨论一种能够抑制ICI影响的最优导频设计方案［7］。导频放置方式如图2所示。

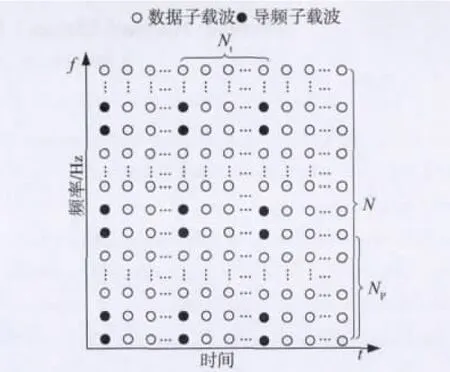
图2 导频结构

由图2可以看出导频在频率和时间上都是等间隔分布，子载波总数为N。时域方向上导频以Nt等间隔放置，导频位置为Pt=r×Nt，其中r=0，1，…，(NOFDM/Nt)－1。频率方向上，导频两个一组，以间隔NP等间隔连续放置，可以分为L=N/NP组。为了抑制ICI，两个相邻导频的选取应满足

式中:np=NP;l=0，1，…，L－1。由式(3)可知，导频符号这样选取是因为两个相近子载波受到其他子载波的干扰几乎相同，频域信道LS估计为

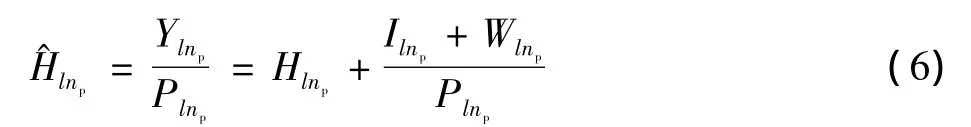
将式(7)中极性相反的符号调制到相邻的子载波上，通过式(8)估计出相邻导频子载波处的频域信道信息，对频域信道估计值进行L点IFFT得到信道抽头时间平均的估计。

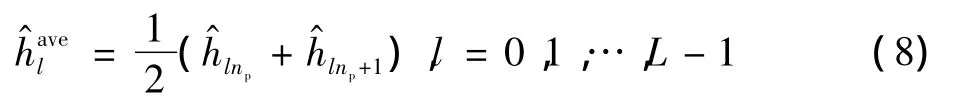
通过对导频处信道估计值进行插值运算得到整个OFDM符号内时域信道信息。然后经过Kalman滤波进行整个时域信道的估计，最后经过时频变换和频域均衡，实现数据的解调。

2.2 自适应Kalman算法

Kalman滤波实现的是实时递推算法，它所处理的对象是随机信号，利用系统噪声和观测噪声的统计特性，以系统的观测量作为滤波器的输入，以所要的估计值作为滤波器的输出，滤波器的输入输出之间是由时间更新和观测更新算法联系在一起的，根据系统方程和观测方程估计出所有需要处理的信号。根据式(2)、式(4)建立以下Kalman状态空间模型，即

式中:vi为均值为qi、方差为Q的高斯白噪声;wi为均值为ri、方差为R的高斯白噪声;Ai，i－1是对角元素为 α(i，j)的状态转移矩阵，i=1，2，…，NOFDM－1，j=1，2，…，N。

Kalman滤波是一种理想的估计器，但是在很多系统本身和外界环境影响的不确定性，给系统噪声和观测噪声统计特性的准确性描述带来偏差，此时根据不确切的模型进行滤波，很可能会引起滤波发散。Sage－Husa自适应滤波利用时变噪声估计器，对系统噪声和观测噪声进行估计和修正，实现抑制发散、提高滤波精度的目的。

Sage－Husa自适应滤波算法［11］可以描述为

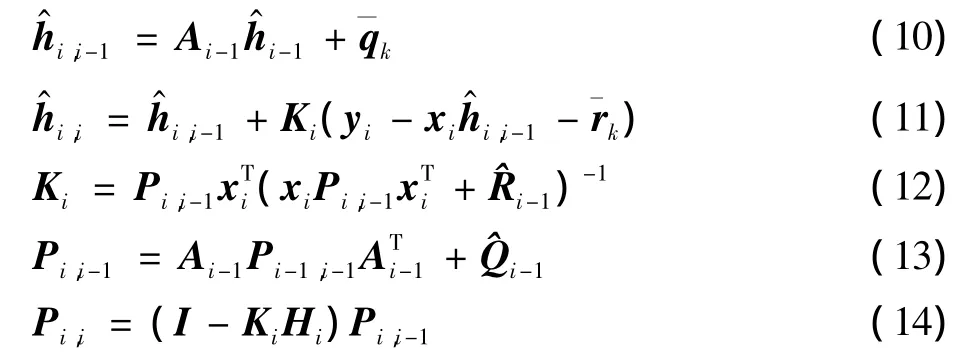
式中:

式中:Ki为Kalman增益矩阵;Pi为估计误差协方差矩阵;b为遗忘因子。

Sage－Husa滤波增加了对噪声统计特性的计算，系统计算复杂度大大增大了，不利于实时性信道估计。而且当噪声失去正定性或半正定性时，系统会失去稳定性和收敛特性，出现滤波发散现象。为确保滤波器的可靠收敛，这里引入一种衰减记忆滤波算法，在传统的Kalman算法的基础上增加一个加权因子S，不对噪声统计特性进行计算，通过增大新观测数据的作用，而相对减小过去数据对滤波的影响，强迫系统滤波收敛。假设系统的噪声统计特性理想已知，令 P0=P0SN，Ri=RiSN－i，Qi－1=Qi－1SN－i，则相对于Sage－Husa滤波方程中式(13)更新为

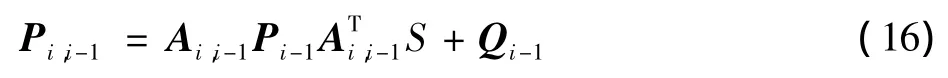
由于加权因子S＞1，使得 Pi，i－1和 Ki的值增大了，相应地加大了当前数据yi在滤波方程中的取值，又因为

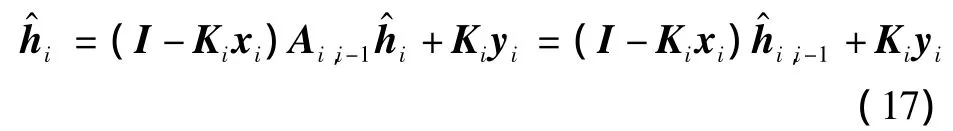
为了克服Sage－Husa滤波器和衰减记忆滤波器各自的缺陷，下面引用一种基于Kalman滤波准则的自适应联合滤波器［11］，这种滤波器将两者结合使用，最大程度发挥各自的滤波优势。自适应联合滤波器的核心思想是，当滤波器不发散的时候系统选取Kalman最优滤波，若存在发散趋势则自动转换为衰减记忆滤波算法。具体算法描述如下:

滤波器发散时估计误差会比理论误差预计值大很多倍，根据这一特点，利用信息序列ei+1=yi+1－xi+1的特性来构成滤波器收敛的判据。信息序列方差阵为

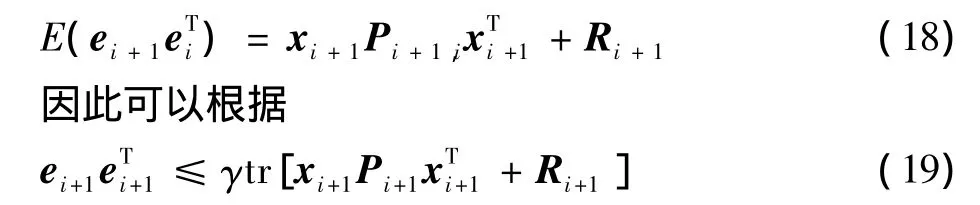
作为滤波器收敛判别依据。其中γ≥1为可调系数。γ=1是最严格的收敛判据条件，此时可得到防止滤波发散的加权因子为

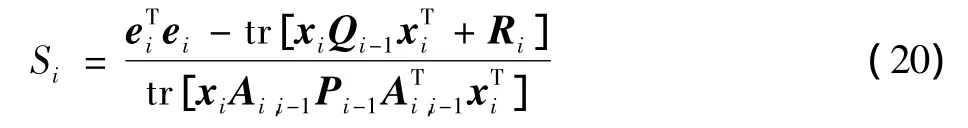
式(19)成立时，可以判定滤波器属于正常工作状态，反之，滤波器工作不正常，处于滤波发散状态。当滤波器工作正常时，运用Sage－Husa算法进行信道滤波，当滤波器处于发散状态时，则调用衰减记忆滤波算法进行滤波发散抑制。

3 仿真与分析

基于上述UWB－OFDM系统模型和提出基于最优导频的Kalman滤波自适应算法，利用MATLAB工具采用0～4 m视距(CM1)室内信道模型进行仿真。系统带宽3.2 ～4.8 GHz，载频子载波个数为 512，循环前缀符号数128，调制方式 QPSK，散射体移动速度 0 m/s，3 m/s，5 m/s。通过仿真对最优导频、自适应联合算法的有效性进行验证。

图3和图4所示为最优导频自适应Kalman算法和传统导频自适应Kalman算法在散射体移动速度为3 m/s时的对比。从图中可以看出添加最优导频后信道估计BER性能极大地提高，随着信噪比的提高，最优导频比传统导频估计性能越来越突出，这是因为信噪比低时，噪声对估计性能的影响比较大。信噪比达到20 dB时最优导频信道估计的MSE曲线性能相对下降了约12 dB，说明了最优导频的有效性。

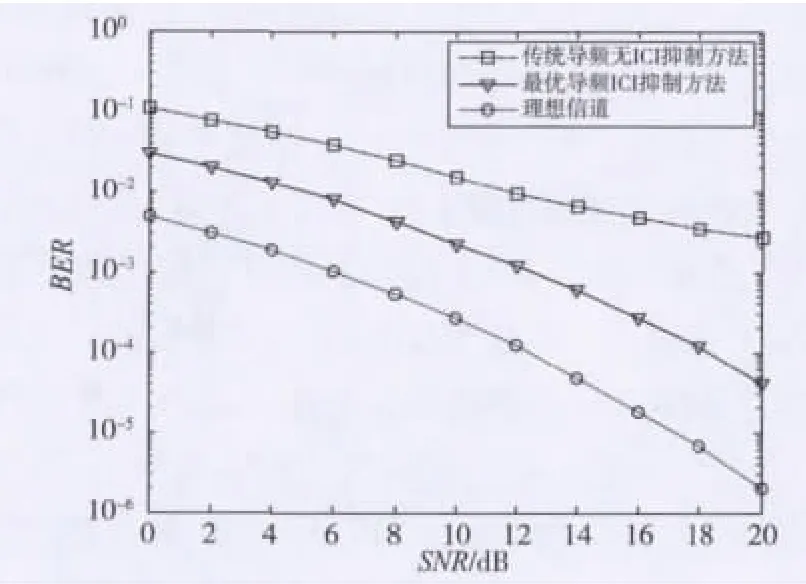
图3 最优导频与传统导频信道估计BER曲线

图4 最优导频与传统导频信道估计MSE曲线

图5给出了散射体不同移动速度下的自适应联合算法的BER性能曲线。可以看出，在系统信噪比较小时，系统的性能主要受输入噪声的影响，而散射体移动的影响不明显。随着信噪比的增大，移动速度对系统的影响就显现出来了，速度越大，信道的时变性越强，从而产生的ICI和其他未知因素引起的模型的摄动对系统的估计性能的影响也就越明显。

图5 不同速度下MSE比较

图6、图7对比了3种Kalman滤波算法的估计性能优劣，可以看出Kalman自适应联合算法在系统性能上相对另外两种方法有明显的提高。当信噪比较低时，Sage－Husa算法滤波性能不理想，有发散的趋势，而衰减记忆滤波性能稳定;随着信噪比的增大，Sage－Husa算法估计精度快速提高，衰减记忆滤波算法则开始出现误码底板现象。自适应Kalman联合算法吸收了两者的优势，表现出良好的估计性能。

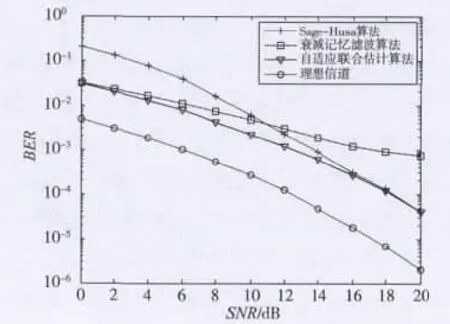
图6 V=3 m/s时3种算法BER比较

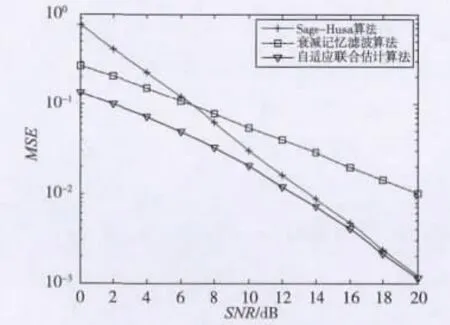
图7 V=3 m/s时3种算法MSE比较

4 结论

本文通过理论分析和计算仿真，对一种基于最优导频设计的自适应Kalman滤波算法在时变UWB信道环境中的性能进行了分析。分析表明，最优导频能有效地抑制ICI，提高信道初始状态的估计准确性;自适应Kalman滤波算法结合了Sage－Husa算法和衰减记忆滤波的优势，在保证滤波器绝对收敛的情况下提高了系统的估计精度。目前对于超宽带时变信道还没有一个成熟的信道模型，时变信道中对Kalman滤波产生影响的不确定因素还很多，然而只对一些相应的问题进行了讨论。关于超宽带的时变信道建模和Kalman滤波在时变超宽带系统中的应用还需要进一步深入研究。

［1］ READ JH.An introduction to ultra wide band communication systems［M］.New Jersey，USA:Prentice Hall，2005.

［2］ AIELLOR.Ultra－wideband wireless systems［J］.IEEEMicrowave Magazine，2003，4(2):36－47.

［3］梁婷，王玲，戴香玉.OFDM系统中时变信道下信道估计方法的研究［J］.电视技术，2007，31(8):68－70.

［4］ FOERSHER JR，PENDERGRASSM，MOSLICH A F.A channelmodel for ultrawideband indoor communication［EB/OL］.［2013－09－10］.http://157.193.140.25/～ mm/Lennert/UWB－channel.pdf.

［5］ LIANG Y M，LUO HW，HUANG JG.Extended Kalman filtering－based channel estimation for space－time coded MIMO－OFDM systems［J］.Journal of Shanghai University，2007，11(5):469－473.

［6］ HAN K Y，LEE SW，LIM JS，et al.Channel estimation for OFDM with fast fading channels by modified Kalman filter［J］.IEEE Trans.Consumer Electronics，2004，50(2):443－449.

［7］ LAN H Y，YANG SY，TAN F，et al.Gradient－based variable forgetting factor RLS algorithm in MIMO－OFDM channel estimation［C］//Proc.International Conference on Wireless communications，Networking and Mobile Computing.Shanghai，China:IEEE Press，2007:468－471.

［8］ ZHAO Y P，HAGGMAN SG.Intercarrier interference self－cancellation scheme for OFDM mobile communication systems［J］.IEEE Trans.Communications，2001，49(7):1185－1191.

［9］ SNOW C，LAMPE L，SCHOBE R.Performance analysis of multiband OFDM for UWB communication［C］//Proc.IEEE International Conference on Communications.［S.l.］:IEEE Press，2005:2573－2578.

［10］张聪，申敏.基于OFDM－UWB系统信道估计方法的研究［J］.电视技术，2008，32(7):63－65.

［11］付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.