改进的基于稀疏表示的多聚焦图像融合
首照宇,胡 蓉,欧阳宁
(桂林电子科技大学a.认知无线电与信息处理省部共建教育部重点实验室;b.信息与通信学院,广西桂林541004)
由于受到光学系统景深的限制,光学照相机很难在一幅图像中使所有目标同时聚焦清晰,而多聚焦融合技术能够有效的解决这一问题,多聚焦图像融合的主要任务就是充分利用不同聚焦点图像的互补和冗余信息得到一幅质量更高,对该场景描述更为准确的新图像,便于人们观察或计算机处理。
近年来,稀疏表示作为一种有效的表示模型广泛应用到信号和图像处理的各个领域,并成功地解决了很多问题,包括图像融合[1-3]、盲源分离、图像去噪[4-5]、图像的超分辨率[6]等。Ahorn[7]等指出图像的特征可以由较少的系数精确表示,过完备稀疏表示采用过完备基代替正交基,用少量元素表示图像特征,由于其基函数具有冗余性,所以过完备基函数相比正交基函数具有更好的稀疏表达能力。稀疏表示融合算法是通过求得稀疏系数来作为信号的特征,对稀疏系数进行融合。
在稀疏分解中,最基本的问题是字典的选择,在选择时需尽可能地符合信号自身的内在结构。根据选择的字典可以将稀疏表示融合算法归为两类:第一类是基于解析字典[8]的稀疏表示算法,这类算法简单,计算复杂度低,但是过分依赖图像的几何特征,不能保证信号的稀疏性,常用的字典有DCT、小波变换[9-10]、Contourlet变换等。文献[1]中LIShutao等提出基于稀疏表示的图像融合与恢复算法,在稀疏分解模型中采用DCT字典,稀疏能力较差。第二类是基于学习字典的稀疏表示算法,通过训练样本,它能够更为准确地从样本数据中提取复杂的图像特征,更好地稀疏表示图像的各种特征,具有很好的自适应性,常用的字典学习的算法有 PCA,MOD,K -SVD[7,11]算法。但由于复杂度的约束限制了在字典学习过程中字典和原子的大小,所以这些字典常用于低维分块数据处理。文献[2]中陈垚佳等提出了一种基于分块过完备稀疏表示的多聚焦图像融合算法(SR),该算法采用K-SVD过完备字典,具有很好的收敛速度,适应性更强,但是SR算法中,对源图像块直接进行稀疏分解,存在有很大的冗余性,并且稀疏分解模型中本身就存在残余量的丢失,融合信息缺乏完整性。
针对以上文献算法存在的问题,本文提出改进的基于稀疏表示的图像融合算法(ISR)。在稀疏分解中,通过采用平均法去除冗余信息,仅对互补信息构成的样本矩阵进行稀疏分解,这不仅能降低计算复杂度,同时也能减少信息的冗余,降低误差。利用小波变换对稀疏表示中的残余信息进一步进行融合处理,这样在最终的融合结果中,没有丢失任何信息,保证了收敛速度。
1 相关工作
1.1 稀疏表示基本理论
稀疏表示是假设自然信号可以由字典的一些原子的线性组合有效地表示或逼近,稀疏表示问题的求解等同于优化问题
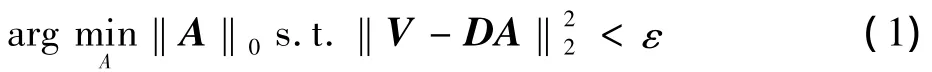
式中:A为样本矩阵V的稀疏表示系数;D∈RN×K(K>N),为过完备字典;‖A‖0为A的l0范数,即向量A中非零元素的个数;ε为逼近误差容限。稀疏逼近问题是一个NP-hard问题,从稀疏分解来讲,有很多种算法来求解这一问题,其中,有三种基本的算法:匹配追踪(MP)、正交匹配追踪[3,12](OMP)和基追踪 (BP)。相比其他两种算法,OMP具有更好的收敛性,是常用的稀疏分解算法。
1.2 SR融合算法
由于稀疏表示可以全局的处理图像,而图像融合则依赖于源图像的局部信息,同时考虑字典的计算复杂度,所以需先对待融合图像A,B进行分块处理,使之成为维数较小的图像块,并将每个图像块转化成列向量,具体分块过程如图1所示。大小为N×N的第j块图像转换成列向量形式,用V j表示,图像A、B所有块构成的样本矩阵分别用V A,V B表示。

图1 源图像分块处理过程
文献[1]提出的方法中,采用滑动窗口步长为1个像素的分块方法,结合OMP与DCT过完备字典进行稀疏分解,但是DCT字典的空间域的局部性差,对边界结构的稀疏能力差,采用了绝对值取大的融合规则,只选取活度级最大的特征,所以会导致图像轮廓过清晰,平滑性较差。
文献[2]提出的SR融合算法对此方法进行了改进,首先对源图像进行分块处理,采用OMP算法结合已训练的K-SVD过完备字典D进行稀疏分解。其中,过完备字典D采用50幅自然图像进行训练得到,采用滑动窗技术将其进行N×N分块(方法与图1相同)构成样本矩阵X,再通过K-SVD算法进行字典训练。绝对值取大的融合规则会使融合图像产生块效应,而平均规则会使融合图像对比度下降,丢失部分细节信息,所以,文献中采用加权平均的规则,对图像异同的特征都进行重构,获得信息量更加丰富。假设系数的稀疏度为cA和cB,稀疏度越大,说明携带的信息量越多,将稀疏系数的活动级作为加权因子wA和wB,加权因子计算方法为

2 ISR融合算法
本文针对文献[2]中源图像块直接进行稀疏分解而存在大量的冗余信息,稀疏分解模型中残余量丢失的缺点,提出改进的基于稀疏表示的图像融合算法(ISR)。
由于同一场景的多幅图像之间存在大量的冗余信息,而图像融合处理主要通过处理图像之间的互补信息来提高图像的清晰度。该算法通过对源图像进行分块,然后求各块的平均值来得到图像之间的冗余信息,仅对去冗余后的互补信息进行稀疏分解,冗余信息保留不变,其原理模型如图2所示。对待融合的源图像A、B进行分块处理,所有块构成的样本矩阵分别用V A,V B表示,而需保留的部分可通过平均值求得,构成平均矩阵V A',V B',而对于待融合的多聚焦图像,每幅图中在不同位置会有模糊部分和聚焦部分,对于两幅图中的同一图像块来说,求得的平均值也有所不同,该算法中采用比较的方式选取最终的平均矩阵V A″,V B″(V A″=V B″),这样会使得图像的信息更加完整丰富,最后得到待稀疏表示的样本矩阵A'=V A-V A',B'=V B-V B'。

图2 冗余处理的原理模型
在稀疏编码中,OMP具有较好的收敛性,但其收敛速度依赖于字典和信号的一致性,当残余图像的量在某种程度上衰减时,它将很难搜索到与残余图像一致的最佳原子,因此,收敛速度会急剧下降,从而影响到整体的融合速度,本文进一步对OMP算法稀疏分解后得到的残余量采用小波变换法进行融合。OMP完成稀疏分解的过程等同于求解优化方程
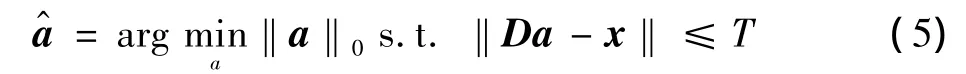
式中:D为训练字典;a为稀疏系数;x为对应样本矩阵A',B'的每一列;T为容限误差;为待求的稀疏系数,在求解式(5)的同时,也可以求出每个稀疏系数的残余量

求得的残余量构成最终的残余矩阵RA,RB,采用小波变换法对残余矩阵进行融合,对高频系数采用绝对值取大,低频系数采用算术平均的融合规则进行处理,通过逆小波变换得到最终的融合的残余量RC。
ISR融合算法的原理如图3所示,具体的融合步骤如下。

图3 图像融合算法框图
1)图像分块。字典原子大小为N2,设两幅大小为M×M的待融合图像A,B,按原子大小逐像素分为P1,P2个N×N大小的图像块,所以每幅图的块数P1=P2=(M+N-1)×(M+N-1),将每个图像块按列向量进行排列,构成样本矩阵VA,VB。
2)去平均。分别对样本矩阵VA,VB各列求平均,得到新的样本矩阵VA',VB',采用式(2)的加权平均法进行比较,得到保留的冗余信息的矩阵VC。
3)稀疏分解。进行稀疏分解的样本矩阵为A'=VA-VA',B'=VB-VB',将A',B'在已训练的K -SVD 过完备字典D上采用OMP算法实现稀疏分解,求得稀疏矩阵A″和B″以及每图像块的残余量,构成残余矩阵RA,RB。
4)稀疏系数融合。本文采用式(2)的加权平均方法对稀疏系数A″和B″进行融合,得到融合系数L,融合系数L与过完备字典D线性组合得到融合图像LC。
5)残余量的融合。采用小波变换对残余矩阵RA,RB进行融合,得到融合图像RC。
6)融合图像。得到最终融合图像F=LC+RC+VC。
7)图像重构。将融合图像F恢复为数据块,并按分块时的顺序重新排列,对重叠块取平均来实现图像重构,最后,得到重构图像f,实现了整个图像融合过程。
3 实验及分析
实验采用2组已配准的大小分别为256×256,240×320的多聚焦图像,如图4所示,对比算法为小波变换法、Contourlet变换法、SR算法。小波变换法采用低频系数加权平均,高频系数绝对值取大的融合规则;基于Contourlet变换法对图像进行5层分解,采用低频系数算术平均,高频系数绝对值取大的融合规则;SR算法是OMP算法与K-SVD字典训练进行稀疏分解,采用加权平均的融合规则。融合结果如图5所示,从视觉效果来看,小波变换法的轮廓比较模糊,Contourlet变换法的轮廓清晰,但轮廓周围出现了严重的虚影现象,这是由于图像在分解过程中进行下采样所致,SR算法得到的融合图像整体偏亮,而本文提出的ISR算法无论从图像的对比度还是清晰度都有较好的效果。

图4 多聚焦图像

图5 融合结果的主观对比图
除了视觉效果外,实验中还采用几种客观评价作为融合图像的评价指标,由于不存在标准图像来进行比较,在客观评价上,本文采用互信息量(MI)、结构相似度(Qabf)、空间频率(SF)、平均梯度这四个指标[13]来评价实验结果。MI反映融合图像从源图像中继承的信息量的多少;Qabf反映融合图像与源图像的结构相似程度;SF反映融合图像空间域总体的活跃程度;平均梯度反映融合图像的清晰程度,其中,MI,SF以及平均梯度越大,Qabf值越接近于1,说明融合性能越好。表1给出了不同融合方法的客观评价指数,可以看出,在两组图像中,小波变换算法的SF明显高于Contourlet算法,略高于SR算法,由于图像性质以及内容的不同,客观指标值也会有所波动,Clock图像中SR算法的总体效果比小波变换算法和Contourlet算法好,但是在Label图像中,总体效果却略差,但是ISR算法在各个评价指标上都要高于其他方法,在性能上得到了较大的提高。

表1 不同融合方法的客观评价指数
4 小结
本文提出一种改进的基于稀疏表示(ISR)的多聚焦图像融合算法。与以往的SR融合算法不同的是,本文仅对去平均后的图像系数进行稀疏分解,降低了图像的冗余性,并对OMP稀疏分解中的残余量进行进一步小波融合,得到重构图像,使图像的信息不会丢失。实验结果证明无论是从主观视觉上还是客观指标评价上,该算法都取得了较好的融合效果,与小波融合算法相比,它能够更好地保留边缘信息和梯度信息,与Contourlet融合算法相比,空间频率得到了很大的提高,与SR算法相比,ISR算法提高了图像的空间细节信息,使图像更加清晰,融合质量更高。但由于ISR算法需进行字典训练,所以在计算效率上比其他算法略低,在后续的工作中,将从字典学习方法以及融合规则方面考虑来进一步提高算法的性能。
[1] BIN Y,LIS.Multifocus image fusion and restoration with sparse representation[J].IEEE Trans.Instrumentation and Measurement,2010,59(4):884-892.
[2]陈垚佳,张永平,田建艳.基于分块过完备稀疏表示的多聚焦图像融合[J].电视技术,2012,36(13):48-51.
[3] BINY,LIS.Pixel-level image fusion with simultaneousorthogonal matching pursuit[J].Information Fusion,2012,13(1):10-19.
[4] ELAD M,AHARONM.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans.Image Processing,2006,15(12):3736-3745.
[5] LIS,FANG L,YIN H.An efficient dictionary learning algorithm and its application to 3D medical image denoising[J].IEEE Trans.Biomedical Engineering,2012,59(2):417-427.
[6] DONGW,ZHANG L,SHIG.Centralized sparse representation for image restoration[C]//Proc.ICCV 2011.[S.l.]:IEEE Press,2011:1259-1266.
[7] AHARN M,ELAD M,BRUCKSTEIN A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Trans.Signal Processing,2006,54(11):4311-4322.
[8] RUBINSTEIN R,ZIBULEVSKY M,ELAD M.Double sparsity:learning sparse dictionaries for sparse signal approximation[J].IEEE Trans.Signal Processing,2010,58(3):1553-1564.
[9] LIX,ROUX M,HEM,etal.A new method of image fusion based on redundantwavelet transform[C]//Proc.VIE 2008.[S.I.]:IEEE Press,2008:12-17.
[10] LEWIS J,O’CALLAGHAN R,NIKOLOV S,et al.Pixel-and regionbased image fusion with complex wavelets[J].Information Fusion,2007,8(2):119-130.
[11] ZELNIK-MANOR L,ROSENBLUM K,ELDAR Y.Dictionary optimization for block-sparse representations[J].IEEE Trans.Signal Processing,2012,60(5):2386-2395.
[12] DAVENPORT M,WAKIN M.Analysis of orthogonal matching pursuit using the restricted isometry property[J].IEEE Trans.Information Theory,2010,56(9):4395-4401.
[13] QU Guihong,ZHANG Dali,YAN Pingfan.Information measure for performance of image fusion[J].Electronics Letters,2002,38(7):313-315.

