一种新的QoS组播路由算法

常国锋，王 满

(1.新乡学院计算机与信息工程学院，河南新乡453003;2.南阳理工学院数理学院，河南南阳473004)

QoS组播路由是下一代Internet需要解决的一个难题［1－2］。而QoS组播路由算法是组播路由的核心技术，要求在分布的网络中寻找一条既满足多个约束条件，同时又满足具有最小代价的最优路径。

BP神经网络通过学习和推理这两个过程，能够修正各个连接途径的权值，无限地逼近样本值，不断修正结果，并且对相关信息实施处理［3－4］。BP神经网络在学习、分类和优化上有优势，有较强的局部搜索能力。蚁群算法(Ant Colony Algorithm，AC)是蚁群能够找到一条从巢穴到食物的最短路径的方法［5］，蚁群算法的优点是具有较强的鲁棒性、分布式计算、易于融合其他算法，同时具有较强的全局搜索能力，但是收敛速度慢、易陷入局部最小点。

本文结合BP神经网络和蚁群算法的优点，提出了一种新型的神经网络蚁群算法(Neural Network Ant Colony Algorithm，NNAC)。结合BP神经网络局部搜索的优势和蚁群算法全局搜索的优势，同时BP神经网络还能弥补蚁群算法易陷入局部最小点的不足。

1 QoS组播路由网络模型

在QoS组播路由网络模型中，通常用加权图G=(V，E)表示通信网络，V表示节点集，E表示链路集，节点数和链路数分别由表示［6－7］。同一对节点间的链路数≤1的网络模型如图1所示。

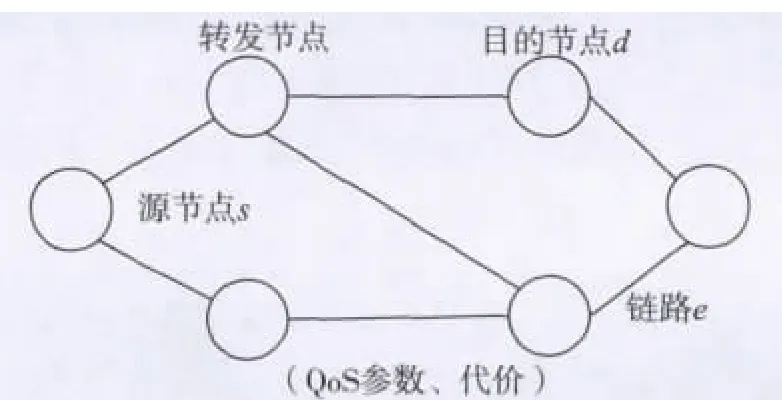
图1 网络模型图

R+、R*分别表示正实数集和非负实数集。数据由源节点s∈V传送到目的节点集D⊆V－{s}，组播组M={s}∪D。定义组播树T=(VT，ET)，组播树T由源节点传送到目的节点的路径为l(s，d)，则对于任意链路e∈E可定义以下QoS参数:

时延函数

带宽函数

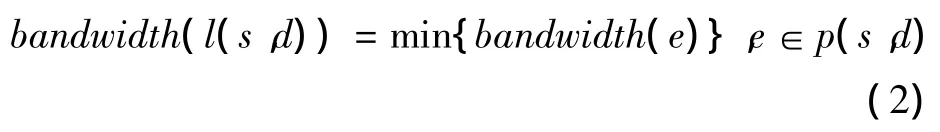
时延抖动函数

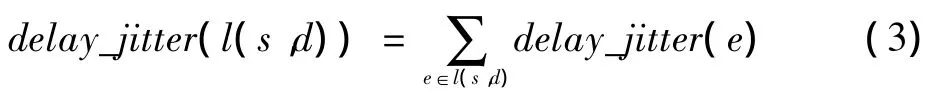
包丢失率函数

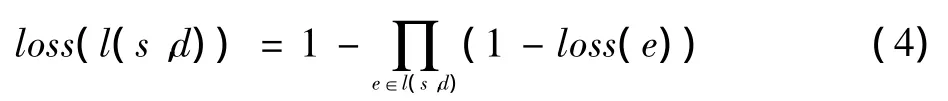
链路代价函数

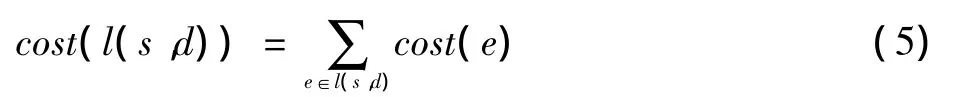
求解多约束QoS组播路由优化问题是指寻找从源节点到目的节点的组播树T，并且满足QoS参数的约束条件

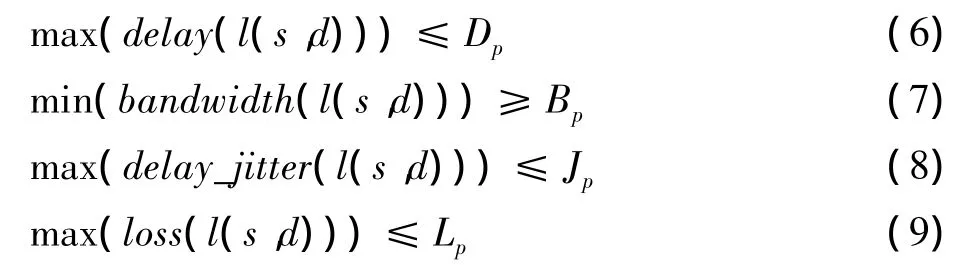
式中:Dp，Bp，Jp，Lp分别为时延、带宽、时延抖动、包丢失率约束量。

2 NNAC算法

结合BP神经网络局部搜索的优势和蚁群算法全局搜索的优势，进行QoS组播路由算法的设计，提出了一种新型的神经网络蚁群算法(NNAC)［8－10］。

2.1 NNAC算法实现步骤

NNAC算法步骤为:

Step1:确定BP神经网络结构，给定BP神经网络权值和阈值;对蚁群算法初始化设置，包括多路径信息强度、蚂蚁数量。

Step2:计算各个路径的适应度。

Step3:从源节点出发，通过赌轮规则选择合适的路径，进行分泌物强度调整。

Step4:将收集的参数作为BP神经网络初始权值和阈值，并对BP神经网络进行训练。

Step5:应用BP神经网络在当前路径中找到更优解，如果有更优解则替代原有路径。

Step6:计算各组播树的代价，判断大部分路径是否收敛于同一组播树，收敛则为最优路径，退出程序;否则，只保留最小代价的组播树，转到Step7。

Step7:返回源节点，转到Step2。

2.2 初始化

初始化中需要设定BP神经网络的权值和阈值para={wi}，wi为N个较小的随机值，N个随机值组成集合，i=1，2，…，N;j=1，2，…，N，设wi对应的信息素为τij，初始时刻、信息素相等，上限为 τ0= τmax。

2.3 路径适应度

NNAC算法依据适应度函数选取路径［8］，选用的适应度函数为

2.4 信息调整

分泌物强度调整函数为

式中:ω为常量参数;l为链路代价。每当蚁群走完一条路径后，需要对所有路径的分泌物挥发性进行调整［9－10］

式中:η为分泌物挥发度;α为各个路径的初始信息强度。

2.5 BP网络训练和调整

BP神经网络采用包括输入层、隐含层、输出层的网络结构［11－13］。在BP神经网络训练时，并不知道准确的输出结果，将Step3中分泌物强度phePj最大的路径和其他路径进行比较，来指导BP神经网络。同时，BP神经网络采用附加动量法进行训练，当修正的权值对误差的影响较大时，应放弃新权值，并停止动量;当新的误差变化率超过设定的最大误差变化率值后，应放弃对权值的变化。最大误差变化率一般设置为1.04。附加动量法判断公式为

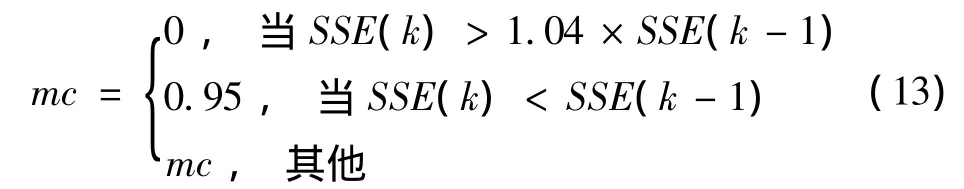
式中:mc为动量因子，取0.95;k为训练次数。

设 BP 神经网络输入向量为 X= ［x1，x2，…，xn］T，输出向量为 Y= ［y1，y2，…，yl］T，期望输出为 D= ［d1，d2，…，dl］T。

BP神经网络的目的就是求误差能量E的最小值，应用BP神经网络在当前路径中找到更优解的方程为

式中:cij表示链路代价;dij表示时延;vij表示神经元的输出;λ→∞ ;能量函数u1项表示代价和时延的最小值;能量函数u2项表示每个节点的出、入边数相等时的最小值，保证从源节点到目的节点为一完整路径。

3 算法仿真分析

首先对NNAC算法全局最小值的寻找进行仿真［14］。由于该算法采用附加动量的BP神经网络进行了训练，所以在附加动量的驱动下，可以避免局部极小值的干扰，从而最终寻找到全局最小值，结果如图2所示。

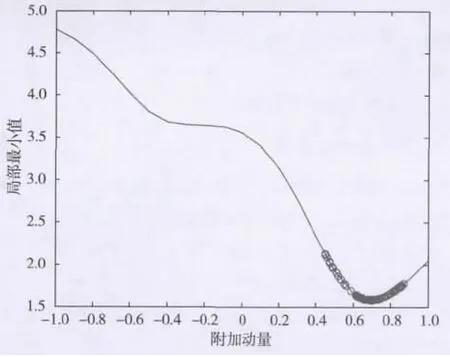
图2 NNAC算法全局最小值寻找结果

对NNAC算法进行仿真分析的网络拓扑结构采用8节点网络结构，如图3所示。拓扑结构图中的源节点为s，目的节点为a，c，e，f，图中各个边上的数值代表延时和代价，用 (Dp，CP)表示，(Dp，CP)的数值是随机的，BP 神经网络误差能量的公式中的u1=1 000，u2=200。

图3 网络拓扑结构图

利用MATLAB编写NNAC算法程序，得到最优组播树如图4所示。通过图4可知，总延时为35，总代价费用为21。

图4 NNAC算法最优组播树

为了进一步分析NNAC算法的性能，引入AC算法，通过两种算法进行最优组播树的寻找成功率进行对比分析，通过实验可以得到如表1所示结果。

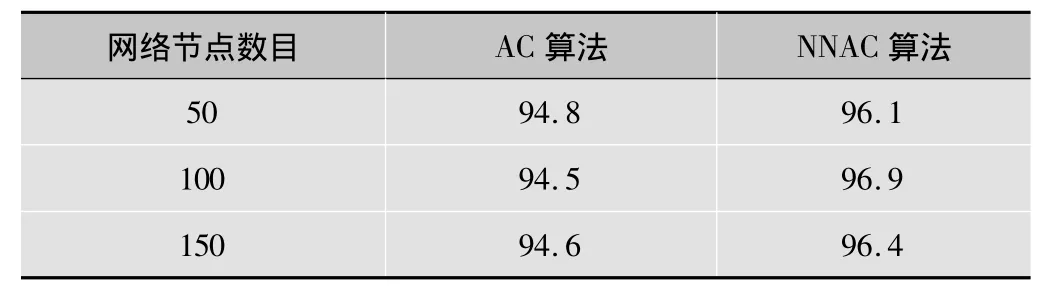
表1 AC算法与NNAC算法成功率对比表 %

通过表1可以看出，两种算法在指定的网络环境下，完成150个度约束组播路由路径时，NNAC算法在进行最优组播树的寻找成功率上高于AC算法。因为NNAC算法融合了BP神经网络局部搜索的优势，克服了易陷入局部最小点的不足。

4 结论

本文结合BP神经网络和蚁群算法，提出了一种新型的NNAC算法。该算法结合了BP神经网络局部搜索和蚁群算法全局搜索的优势，改善了QoS组播路由路径寻找的方法。通过实验仿真分析，NNAC算法能够有效地提高最优组播树的寻找成功率，同时该算法还克服了AC算法易陷入局部最小点的不足。

［1］葛连升，江林，秦丰林.QoS组播路由算法研究综述［J］.山东大学学报:理学版，2010(1):55－65.

［2］黄小凤.计算机网络中的组播路由算法研究［D］.长沙:湖南大学，2010.

［3］刘建国.基于卡尔曼滤波的BP神经网络模型在桥梁形变中的应用［D］.西安:长安大学，2010.

［4］ YANG B.BP neural network optimization based on an improved genetic algorithm［C］//Proc.2002 International Conference on Machine Learning and Cybernetics.［S.l.］:IEEE Press，2002:64－68.

［5］ TSENG Shengyuan，LIN Changchun，HUANG Yuehmin.Ant colonybased algorithm for constructing broadcasting tree with degree and delay constraints［J］.Expert Systems with Applications，2008，35(3):1473－1481.

［6］陈杰，张洪伟.基于自适应蚁群算法的QoS组播路由算法［J］.计算机工程，2008，34(13):200－20.

［7］丁国强，孙泽宇，李传锋.改进遗传蚁群算法求解优化问题的设计与实现［J］.计算机测量与控制，2011，19(10):2558－2561.

［8］王兴伟，邹荣珠，黄敏.基于蚂蚁算法的ABC支持型QoS组播路由机制［J］.东北大学学报:自然科学版，2009，30(7):959－963.

［9］孙力娟，王汝传.基于蚁群算法和遗传算法融合的QoS组播路由问题求解［J］.电子学报，2006，34(8):1391－1395.

［10］葛连升，王华，王海洋.求解度约束组播路由的新型蚁群算法［J］.电子学报，2009，37(7):1447－1551.

［11］ LIUW，WANG L.Solving the delay constrainedmulticast routing problem using the transiently chaotic neural network［J］.Advances in Neural Networks(ISNN):LNCS，2007(4492):57－62.

［12］ WANG L，LIUW，SHIH.Delay－constrained multicast routing using the noisy chaotic neural networs［J］.IEEE Transa.Computers，2009，58(1):82－89.

［13］陈阳舟，田秋芳，张利国.基于神经网络的城市快速路交通拥堵判别算法［J］.计算机测量与控制，2011，19(1):167－169.

［14］尚涛，谢龙汉，杜如虚.MATLAB工程计算及分析［M］.北京:清华大学出版社，2011.