利用改进遗传算法优化载人机动装置飞行轨迹
冯 昊,李新明,潘 豪
(北京航天自动控制研究所,北京100854)
1 引言
航天员舱外活动(EVA)是当今最危险、最耗资的载人航天技术之一,EVA控制技术是研究航天员驾驶载人机动装置(MMU)与空间站(SS)分离,到达相对空间站周围的某一固定位置,或去捕捉一个有相对运动的空间飞行目标,可以再补给并可重复使用的MMU技术[1]。
MMU能够为太空舱外活动的航天员提供轨道和姿态机动能力,让航天员安全、迅速、无碰撞的完成靠近飞行各种空间作业的空间“行走”机械装置,所带推进剂总是有限的,在变轨过程中,尽量减少推进剂消耗,可以增加飞行器的有效载荷、延长在轨使用时间,提高经济效益。因此节省推进剂、时间短的轨迹优化问题,一直是研究人员很感兴趣的问题[2,3]。基于 CW-HILL 方程的脉冲控制方法[3]能够使推进剂消耗达到最优,其线性形式也适合星载计算机进行星上计算,但是其精度不高。随着计算机硬件性能的提高,计算机的处理能力越来越强大,这就为采取更复杂但更精确的算法提供了可能。在硬件水平允许的条件下,研究更先进的控制算法,可以得到更高的精度。
目前,一般的优化设计方法如极大值原理可以将优化轨迹的求解归结为一个关于两点边值问题的求解,但它对迭代初值的选择十分敏感;动态规划算法可以得到问题的最优解,但具有维数爆炸特性,其本质是一种枚举法;梯度法、模拟退火法等则容易陷入局部最优;而遗传算法是一种模拟生命进化机制的搜索算法,其算法简单,同时又具有鲁棒性、隐含并行性的特点,能得到全局最优解[4]。因此,从算法的实用性、解算的精度及运算时间三方面考虑,本文基于遗传算法(GA)进行分析研究。
MMU在空间站附近的相对运动可以用航天器近距离相对运动方程[5]来描述,在执行救援任务时,使其变得复杂的原因是MMU的飞行轨迹被要求,从空间站、航天飞机出来后,在任何时刻都不能碰撞到空间站、航天飞机。目前现有可以查阅到的文献中没有考虑飞行过程中障碍物的存在,因此本文从工程实际出发,进一步针对救援过程中存在如航天飞机机翼这一类障碍物的情况,利用GA对MMU的飞行轨迹进行了有意义的研究和优化设计,得出了一些有价值的结果。
2 分析模型
为了对MMU执行救援任务的飞行轨迹进行优化设计,首先要建立数学模型。采用的轨道坐标系的原点位于空间站的质心,z轴指向地心,x轴指向空间站的运动方向,y轴指向轨道面法向。准圆形轨道中运动的角速率为ω,两个相近轨道航天器的相对运动可用如式(1)所示的Clohessy-Wiltshire 方程[5]描述。

其中x、y、z是主动飞行器(MMU)的坐标,ω是空间站在近圆轨道上绕地球转动的角速度,这里取ω为常值。求解方程(1),当初始条件(x0、已知时,得其解析解如式(2)(3)。

和

MMU的救援飞行轨迹可分为6个阶段(如图1 所示),定义[3]如图1。

图1 MMU系统救援轨迹示意图Fig.1 Schematic diagram of the MMU rescue trajectory
DT1:目标分离和MMU发射(弹射分离)之间的初始延迟时间;
DT2:MMU发射和目标(待救航天员或捕捉失效的卫星或飞到指定的防热瓦部位)交会之间的第一个自由飞行段;
DT3:MMU到达目标,并与其进行对接,DT3结束时刻,MMU和目标对接完成,但还没有准备好返航;
DT4:对接后段,航天员将目标紧固在MMU上,并转动到合适的角度进行返航,DT4结束时刻,MMU执行返航点火;
DT5:第二个自由飞行段,DT5结束时刻,MMU到达空间站并点燃推进器进行减速;
DT6:MMU慢慢地到达SS,DT6结束时刻,MMU与空间站对接。
DV1:将MMU发射到相对于目标的最优交会轨迹上所需要的Δv;
DV2:在与目标交会中,匹配目标速度所需要的Δv;
DV3:将MMU和目标组合置于向空间站的返回轨迹上需要的Δv;
DV4:靠近空间站时进行制动所需要的Δv。
表1给出了DT1—DT6的最小约束值[3]。
MMU的推进剂消耗可以用理想的火箭方程[2]计算得到如式(4)所示结果。

其中ve是推进剂喷出速度,m是运载器机动初始质量,Δv是运载器速度增量,Δm是产生Δv所消耗的推进剂质量。

表1 DT最短飞行时间的约束值Table 1 The shortest flight time constraint values
2.1 设计变量、约束条件和优化目标
由C-W方程的解析解(2)和(3)式,当已知目标的初始速度和位置时,可以计算得到任意t时刻目标所在的位置和速度;对于执行捕捉目标的MMU,当已知MMU的初始位置和t时刻目标所在的位置,通过(2)式可以计算出t时刻MMU飞行到目标所在位置所需要的初始速度增量,通过(3)式可以计算出t时刻MMU的速度,进而得到MMU与目标交会中匹配目标速度所需要的速度增量。由此可知MMU救援过程中所需要的DV1、DV2、DV3、DV4 是时间 DT1、DT2、DT3、DT4、DT5、DT6和目标初始条件(x0、y0、z0、x·0、y·0、z·0)的函数,而推进剂消耗是Δv的函数(如(4)式所示)。这样最小推进剂消耗问题就简化为一个参数最优化问题,状态向量由6个DT组成。
而 DT1、DT3、DT4、DT6 应尽可能小,因此DT1、DT3、DT4、DT6可以从最优化过程中去掉,取其各段的最小允许值。而DT2、DT5为自由飞行段时间,不受约束,对于给定的初始条件,这两个变量就决定了MMU的最小推进剂飞行轨迹,因此确定DT2、DT5为设计变量。
MMU从空间站、航天飞机出来和返回过程中,任何时刻都不能碰撞到空间站、航天飞机,在优化设计MMU救援轨迹时必须考虑在飞行过程中存在如航天飞机机翼这一类障碍物的情况,因此将禁飞区(包括航天飞机的舱体、垂直尾翼、翼展)作为约束条件。
MMU舱外活动依据任务的性质不同,一般不只单对推进剂消耗或单对时间有要求,而是对推进剂和时间都有要求,是能量与时间综合优化的问题,因此可以对能量与时间优化指标进行线性加权处理,其优化指标可以表示为公式(5)。

当考虑禁飞区约束时,通过采用惩罚函数法[4],可以将有约束的优化问题变为无约束的优化问题。经过这样的处理,MMU飞行轨迹的优化指标可表示为公式(6)。

其中Δmi为各DT段MMU推进器的推进剂消耗,D为MMU飞行轨迹进入到禁飞区内的点数,k1为推进剂消耗量加权系数、k2为飞行时间加权系数、k3为惩罚系数;k3取值较大,以使进入禁飞区的劣质个体具有较低的适应度,加速其淘汰。
经过上述分析,本文选取DT2、DT5为设计变量。由式(2)和(3)可以确定 DV1、DV2、DV3、DV4,进而确定推进剂消耗,并通过惩罚函数法处理避开禁飞区的约束问题。利用多起始点的GA,在全局范围内搜索MMU飞行过程中能够避开禁飞区的最少推进剂飞行轨迹。
3 遗传算进行MMU飞行轨迹优化的方法及步骤
1)确定决策变量及各种约束条件,即确定出个体的表现型和问题的解空间。在本文的优化设计中,决策变量即为所选取的设计变量 DT2、DT5,解空间为设计变量所允许的最大时间约束,均设为20 min。
2)建立优化模型,即确定出目标函数的类型及数学描述形式。本文的目标函数表达式及含义见式(5)、(6)。
3)确定可行解染色体的编码方法,也即确定出个体基因型及遗传算法的搜索空间。本文采用二进制编码方案,根据决策变量的上、下界及所要求的时间精度(至少要满足MMU喷气发动机开关机时间精度)确定 DT2、DT5的编码长度为15位。
4)确定解码方法,即确定出个体基因型到个体表现型的对应关系或转换方法。本文的二进制编码的解码公式为表现型=设计变量区间长度×基因型/pow[2(编码长度-1)]-设计变量的区间左端点值。
5)确定个体适应度的量化评价方法,即确定出由目标函数值到个体适应度的转换规则。因本文的优化目标是求函数的最小值且函数值均为正值,故可取其倒数作为评价个体的适应度。
6)设计遗传算子。
基本遗传算法[4]是基于采用适应度比例选择、单点交叉和单点变异的遗传算法。其主要不足是收敛速度慢,不成熟收敛等。为克服这些缺点,本文在基本遗传算法的基础上,对各种算子进行了改进,提出了新的改进遗传算法。
1)最优解保存法:选择的过程是利用解码后求得的各个体适应度的大小,淘汰一些较差个体而选出一些比较优良的个体,以进行下一步的交叉和变异操作。本文采用了最优保存策略和比例选择相结合的方法,即首先找出当前群体中适应度最高的个体,为保证当前最佳个体不被交叉和变异所破坏,允许其不参与交叉和变异而直接进入下一代,然后剩下的个体按比例选择法操作。引入最优保存策略,可以不断提高群体的平均适应度,而且能保证最佳个体的适应度不减小。
2)优劣个体相互交叉法:GA中的交叉算子是遗传操作中产生新个体的主要方法。本文在单点交叉的基础上引入优劣个体相互交叉的策略,即在种群遗传过程中,要按照个体适应度高低进行排序,然后将群体中一定数量适应度高的优良个体与相应数量适应度低的劣质个体两两配对,对每一个体对产生一个随机数r∈[0,1],若r大于交叉概率Pc,则在两两配对的个体编码串中随机设置一个交叉点,然后在该点相互交换两个配对的优良个体和劣质个体的部分基因,从而生成子代两个新的个体。这种方法不但可以避免近亲交叉,还可以使最优个体在整个种群中得以继承。
3)非一致性变异法:对于二进制基因串而言,变异操作就是按照变异概率Pm,随机选择变异点,在变异点处将种群中某些基因位取反,变异概率一般很小。本文采用基本位变异法,种群中每个个体的每一位依相同的概率Pm发生变异,在此基础上引入非一致性变异策略,从第2代开始在变异过程中,随机产生一定数量的新个体,并用新产生的个体代替种群中适应度较低的个体。这种方法在变异过程中可以维持种群的多样性,避免因变异概率小出现未成熟而收敛的现象。
4)确定GA的运行参数,如种群大小、交叉概率、变异概率等。本文取种群大小为200,进化代数为100,交叉概率为0.6,变异概率为0.1。
4 仿真优化结果与分析
本文仿真实例中,假设目标的初始位置是(0,0,0),初始脱离速度的大小为 1.732 m/s,方向共分为9种典型情况[3],如图2所示。MMU的初始位置是(0,0,0),DT1、DT3、DT4 取表1 中的最小约束值,DT2、DT5的最大约束时间均为20 min。设MMU及航天员的质量为110 kg,目标质量为120 kg,推进剂喷射速度为588 m/s。

图2 目标初始分离速度的方向Fig.2 The initial separation velocity direction of target
4.1 理想情况下求解能量-时间综合优化问题
本文首先研究了飞行过程中不存在障碍物的理想情况下,目标和MMU在轨道面外的运动情况,根据MMU飞行轨迹的优化指标(5)式,应用上面所设计的遗传算法求取MMU的满足其喷气发动机开关机时间精度(0.02 s)要求的最小推进剂解的计算结果见表2。如目标的初始脱离状态以第3种情况为例(初始脱离速度为(1,1,1)),则在轨道平面外理想情况最小推进剂飞行轨迹见图3所示。本文研究时将航天飞机几何外形简单描述为如图4,在叠加了航天飞机的图例后,相应的救援轨迹在返回时航天飞机附近的轨迹放大部分见图4所示(图中“——”线型表示目标的运动轨迹,“…”线型表示MMU的救援轨迹,“-”线型表示MMU与目标交会后的滑行段运动轨迹,“.-”线型表示MMU与目标返回过程运动轨迹,“o”处表示初始位置,以下均同)。
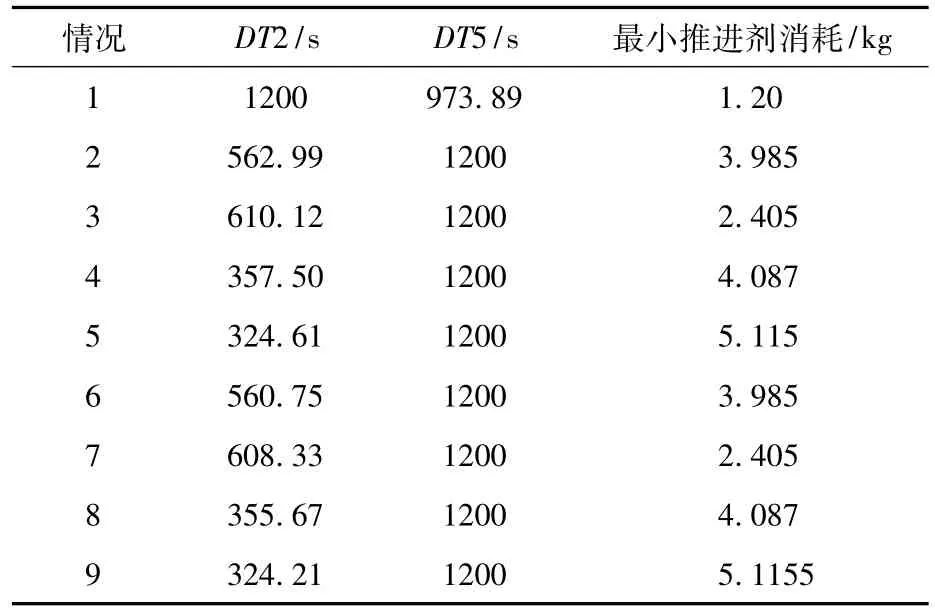
表2 理想情况MMU舱外救援的最小推进剂消耗Table 2 Minimum fuel consumption under the ideal situation

图3 理想情况MMU最小燃料救援轨迹Fig.3 The minimum fuel rescue trajectory under ideal situation

图4 理想情况叠加航天飞机时最小燃料救援轨迹局部放大图Fig.4 The partial enlarged detail of the minimum fuel rescue trajectory under ideal situation with the space shuttle
从仿真结果可以看出,通过GA可以搜索得到满足MMU喷气发动机开关时间精度要求的最小推进剂解;并从飞行曲线图3和图4,可以看出单纯研究以最小推进剂为优化指标的飞行轨迹在MMU返回过程中与航天飞机发生碰撞,这不但严重威胁航天员的安全,也会损坏航天飞机,这样的救援方案并不可行。
4.2 救援过程存在障碍物时的优化轨迹
针对前面提出的实际问题,本文进一步利用改进遗传算法搜索能够避开障碍物(对于MMU,航天飞机机身、机翼可视为障碍物),使MMU安全飞行并尽量节省推进剂消耗的救援轨迹。
在优化过程中,如(6)式所示,所研究问题的目标函数采用线性加权的方法,k1,k2,k3是可调的权系数。在利用GA解决绕障碍物的问题时,为了使碰到障碍物进入禁飞区的个体具有较低的适应度,k3取值较大;但也不要过大,以避免造成GA的选择压力过大,破坏了种群的多样性,使GA过早收敛,而无法搜索到全局最优值。
算例如前所述,进一步考虑MMU救援过程中障碍物的存在对其飞行轨迹的影响。假设目标从航天飞机有效载荷舱的顶部附近脱离,MMU进行营救任务。同样目标的初始脱离状态以第3种情况为例(初始脱离速度为(1,1,1)),通过 GA搜索到的能够使MMU避开障碍物安全返回舱内的飞行轨迹如图5所示,相应的在航天飞机附近救援轨迹放大部分如图6所示。
由仿真结果我们可以看出,虽然MMU能够避开障碍物飞行的轨迹是以推进剂消耗为代价的,但应用本文的综合优化指标,我们也可以做到在确保安全的前提下,尽可能节省推进剂的消耗。
本文仅以目标初始脱离速度沿第3种情况为例进行介绍,当目标初始脱离速度的大小、方向不同、MMU与目标交会的时间不同以及整个营救过程遇到的障碍物几何构型不同,则MMU绕障碍物飞行的轨迹也不同,但无论何种情况,采用本文的研究方法,可以确保MMU在安全完成救援任务的同时尽可能减少推进剂消耗。

图5 MMU安全完成救援的飞行轨迹Fig.5 Safety flight rescuing trajectory

图6 MMU避开障碍物飞行时的局部放大轨迹Fig.6 The partial enlarged detail of avoiding obstacles flight trajectory
5 结论
本文从载人机动装置实际飞行任务需求出发,在确保安全的前提下进行空间舱外救援,研究了以能量-时间为综合优化目标的MMU飞行轨迹,并设计了相应的改进遗传算法;不但可以在全局范围搜索到MMU的优化轨迹,其隐含的并行性使问题的处理时间也相应缩短。本文仿真所得到的MMU能够绕过障碍物飞行的轨迹在理论研究同时对工程实践不断提出的新问题进行了一次十分有意义的探索研究。
[1]陈善广.航天员出舱活动技术[M].北京:中国宇航出版社,2007:1-5.
[2]Neff M,Fowler W T.Minimum-fuel rescure trajectories for the extravehicular excursion unit[J].The Journal of the Astronautical Sciences,1991,39(1):21-45.
[3]周荻,慕春棣,王旭东.载人机动装置救援轨迹优化设计[J].宇航学报,2000,4:19-26.
[4]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:35-60.
[5]郗晓宁,王威.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003:10-21.

