基于李雅普诺夫函数的航空发动机非线性控制设计方法

商国军，王继强，夏 超，胡 欢，赵明宇

（南京航空航天大学能源与动力学院，南京210016）

0 引言

航空发动机是1个复杂的热机械系统，其本质是1个强非线性对象，在飞行包线内参数变化范围大，线性模型只能在发动机的某个稳定工作点附近有效。然而发动机工作在范围很大的包线区域，且发动机状态变化范围较宽，所以用基于线性模型设计的控制规律不能很好地满足系统变工况运行的需要。尤其在环境有较大改变时，所提取线性模型的准确性将受到影响，系统鲁棒性的保持成为1项困难的问题[1-2]。因此航空发动机的动态过程必须由非线性数学模型来描述，这就需要非线性控制技术来完成控制系统的设计研究。目前，已经提出了几种可行的非线性控制方法，文献[3]提出了反馈线性化与滑模控制的方法有效应用于航空发动机不稳定燃烧主动控制中；文献[4]介绍了1种基于遗传算法的航空发动机模糊控制方法，取得了比较好的控制效果；文献[5]提出了成功应用于航空发动机控制的非线性预测控制方法。

本文采用李雅普诺夫方法，在保证系统稳定的前提下，设计出航空发动机非线性控制器，有效改进了航空发动机控制系统的性能。

1 航空发动机非线性控制设计

李雅普诺夫理论[6-8]主要是借助于1个李雅普诺夫函数直接对系统平衡状态的稳定性做出判断，从能量的观点进行稳定性分析，其判断方法可依据李雅普诺夫稳定性定理：如果在1个球BR0内，存在1个标量函数V（x），具有1阶连续偏导数，并且V（x）正定（在球BR0内）；（x）负半定（在球BR0内）。那么平衡点0是稳定的，如果导数（x）在球BR0内是负定的，那么0是渐近稳定的。

航空发动机的非线性模型[9-11]可以表示为

在某一确定的稳态点，通过泰勒级数的展开可得到状态空间模型的表达式为

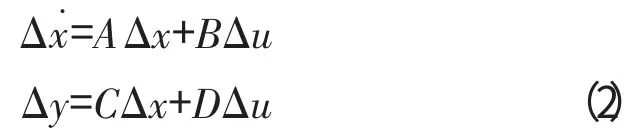
例如将燃油流量比Wf作为控制输入量；将压气机及风扇转速nH，nL作为状态变量，则状态方程可表示为

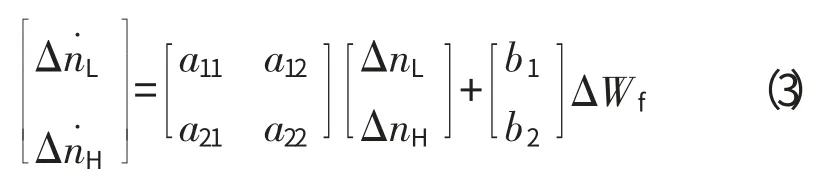
方程中的参数可通过偏导数法[12]或拟合法[13-14]求得。显然上述模型只有在稳态操作点才有效。因此，为得到更大包线内的控制模型，其中1种方法是为模型添加非线性项，以此来修正线性模型。例如

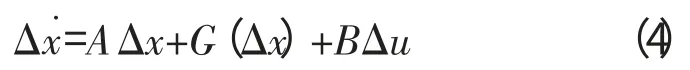
式中：G（·）为一般的非线性项。

为了方便表述，式（4）可简化为

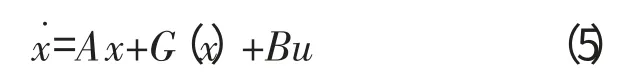
尽管G（x）的引入带来了系统的非线性，且需要非线性设计技术的支持，但系统的控制性能可在较大的飞行包线下得到改善。

本文采用的航空发动机模型[15]可表示为

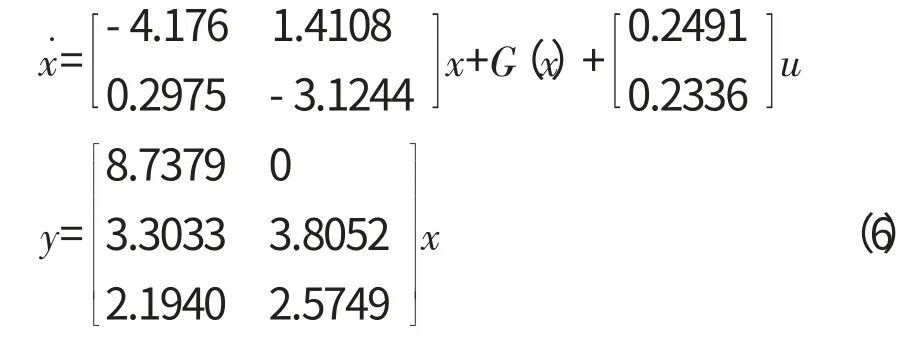
在式（6）中，由于线性模型部分只适用于转子转速在2%~3%范围内变化，为了使该线性模型在更大包线范围内有效，可用试测法选取非线性函数G（x）加入到线性模型中，使新建立的模型可适用于转子转速在5%左右范围内的变化，有效拓宽了该模型的适用范围。其中非线性函数G（x）为

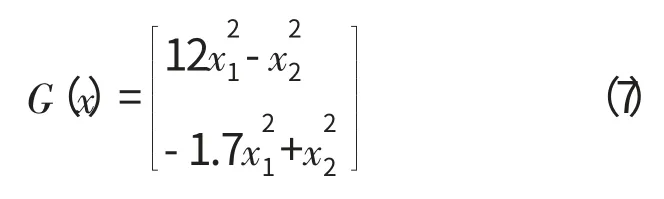
在G（x）函数中存在状态变量的交互作用，表明了航空发动机复杂的动态性。

输入量u=ΔWf，输出量yT= [PCN2R P56/P25P16/P56]T。静态反馈控制为

式中：

非线性控制设计的问题就是寻找1个常数矩阵使状态x（t）在约束条件下是稳定的。

下面应用李雅普诺夫直接法分析航空发动机非线性控制系统稳定性问题。首先令Lyapunov函数

其中

Lyapunov函数V（x）的1阶导数为

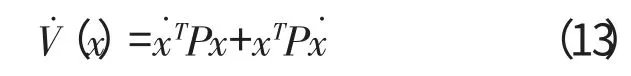
将式（5）、（8）代入式（13）中得

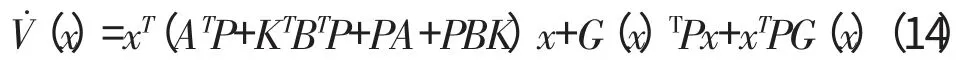
由李雅普诺夫稳定性定理可知，系统在平衡点处是渐进稳定的条件为V（x）>0；V˙（x）<0。

将式（7）、（9）、（11）、（12）以及式（6）的状态方程系数矩阵代入式（14）得

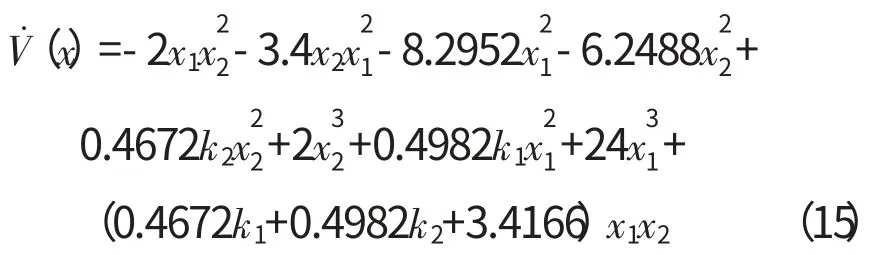
对式（15）合并同类项得

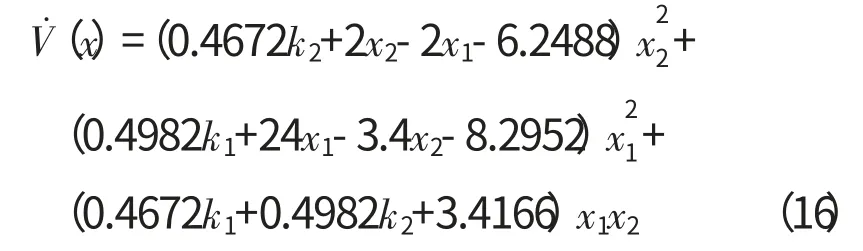
式（16）可转化为

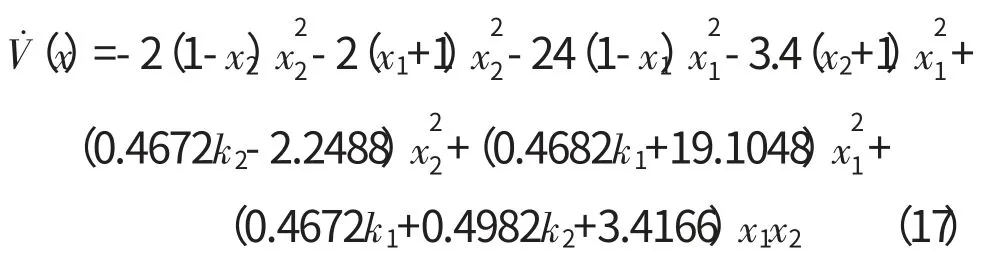
显然，在式（17）中

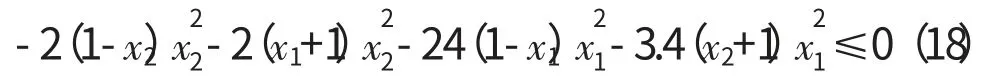
恒成立。

要使式（17）V˙（x）<0，只需使式（19）成立，即

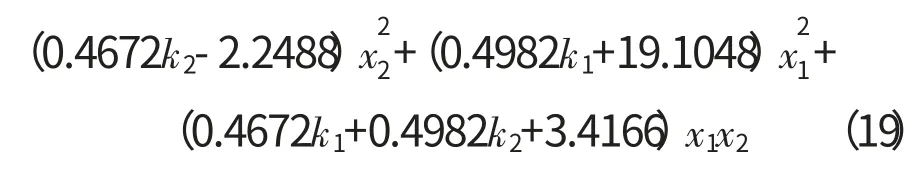
使式（19）成立的充要条件为

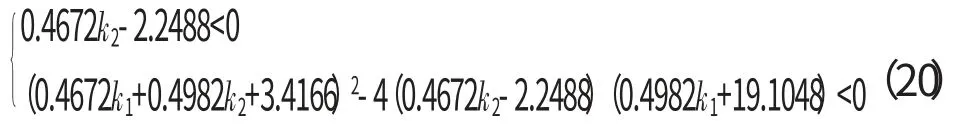
将式（20）化简得

由式（21）可得控制器参数的有效选择范围，如图1所示。

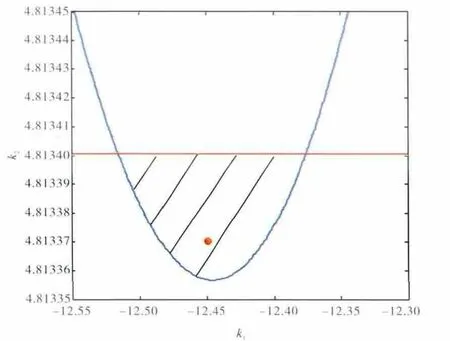
图1 控制器参数的有效选择范围

显然，由式（21）可知，要保证系统稳定，控制器参数K 应在图1中2条线所围成的阴影内选取，如取K=[-12.45 4.81337]，即k1=-12.45，k2=48.1337，将其代入式（21）中，可使该不等式组成立。

综上所述，当常数矩阵K 在图1阴影内部取值时可满足李雅普诺夫稳定性定理，即状态变量 在约束条件下是稳定的。

2 航空发动机非线性控制数值仿真

2.1 调节器设计

当发动机工作在稳态时有u=ΔWf=0，首先考虑调节问题，本文研究的目的是设计u=ΔWf=Kx，使状态变量x 及输出变量y 的瞬态性能得到改进。

取状态反馈矩阵K=-[-12.45 4.81337]，在初始状态为x0=[0.2 0.3]T时进行系统仿真。

x（t）的瞬态性能如图2所示，图中也绘出了系统在无反馈控制下x（t）的瞬态响应，即为零输入响应。

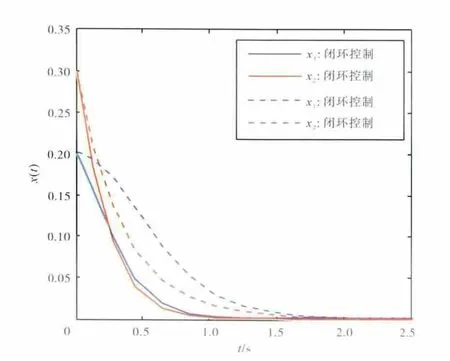
图2 状态信号瞬态响应的比较，x0=[0.2 0.3]T

从图2中可见，在闭环状态反馈的作用下，系统调节时间短，响应快，控制系统性能得到明显改善。

yT=[PCN2R P56/P25P16/P56]T输出信号的调节性能如图3所示。图3绘制出了系统在开环控制下y的瞬态响应，曲线表明状态反馈控制提高了系统输出变量的调节性能，瞬态响应速度快，调节时间短，发动机能有效抑制干扰，是航空发动机控制系统的1个重要特性。

2.2 跟踪性和鲁棒性

燃油流量比ΔWf的增量代表了航空发动机的加速过程。对于ΔWf的阶跃输入需要PCN2R 的快速响应。在某飞行高度H 及飞行Ma 下，涡扇发动机高压涡轮转速的响应速度可作为飞机机动性能的衡量标志，如图4所示。为便于比较，图中也绘出了相应线性系统的开环与闭环响应曲线，其中作为比较的开环控制规律皆为零状态响应。

（1）从图4中可见，非线性系统与线性系统在同样状态反馈控制下，控制系统的瞬态响应性能得到明显改善，表明系统具有良好的跟踪性。

（2）通过比较可得，原线性系统所引入的非线性项可作为对线性系统的1种干扰，但它并没有影响系统的性能，且所应用的非线性控制设计方法使系统具有良好的跟踪性，表明系统具有较好的鲁棒性。

（3）真实系统的动态性应由非线性系统来表示，在图4中尽管开环系统性能有所下降，但闭环系统能够保持较好的性能。实际上，对闭环非线性系统与闭环线性系统的性能比较表明系统性能的损失是有限度的。说明所提出的设计方法可适应对象大范围的变化，这也正是控制系统所期望的特性。

仿真结果表明：本文提出的设计方法使系统达到了期望的性能，系统响应快，能有效抑制干扰，且具有较好的跟踪性及鲁棒性。验证了基于Lyapunov方法的航空发动机非线性设计方法的有效性。

3 结论

（1）通过应用Lyapunov方法，使状态反馈矩阵K在一定范围内选取的条件下，保证控制系统的稳定性。因此，可进一步提高控制系统获得最佳性能的可能性。

（2）通过对控制系统的数值分析及仿真研究表明：本文提出的设计方法使航空发动机非线性控制系统的性能得到改善，在航空发动机非线性控制方法研究中具有一定参考价值。

（3）该方法只保证了K 取一定范围内控制系统的稳定性，对于如何进一步选取K 的取值以保证控制系统的动态性能，以及对收敛速度做进一步分析，可作为下一步的研究方向。

[1]孙海东,尚永锋.航空发动机控制系统[J].微计算机信息，2007，23(6-1)：65-66.SUN Haidong，SHANG Yongfeng.The aeroengine control system[J].Microcomputer Information，2007，23(6-1)：65-66.(in Chinese)

[2]张海波,孙健国,孙丰诚.非线性反演控制律在航空发动机多变量控制中的应用 [J].航空动力学报，2007，22（7）：1190-1194.ZHANG Haibo，SUN Jianguo，SUN Fengcheng.Applications of nonlinear backstepping control strategy in multivariable control of aeroengine[J].Journal of Aerospace Power，2007，22（7）：1190-1194.(in Chinese)

[3]董飞，何国强，刘佩进，等.反馈线性化与滑模控制方法在发动机不稳定燃烧主动控制中的应用[J].测控技术，2007，26（6）：40-44.DONG Fei，HE Guoqiang，LIU Peijin，et al.Application of feedback linearization and sliding mode control to unstable combustion in engine[J].Measurement&Control Technology，2007，26（6)：40-44.(in Chinese)

[4]张世英，胡宇，朱杰堂.基于遗传算法的航空发动机模糊优化控制[J].弹箭与制导学报，2010，30（2）：167-170.ZHANG Shiying，HU Yu，ZHU Jietang.Optimization of aeroengine fuzzy control based on genetic algorithm[J].Journal of Projectiles，Rockets，Missiles and Guidance，2010，30（2）：167-170.(in Chinese)

[5]Brunell B J，Bitmead R R，Connolly A J.Nonlinear model predictive control of an aircraft gas turbine engine[C]//Proceedings of the 41st IEEE Conference on Decision and Control，USA，2002.

[6]斯洛坦，李卫平.应用非线性控制[M].北京：机械工业出版社，2006：28-77.Eslotine J J，LI Weiping.Applied nonlinear control[M].Beijing：China Machine Press，2006：28-77.(in Chinese)

[7]贺昱曜，闫茂德.非线性控制理论及应用[M].西安：西安电子科技大学出版社，2007：42-90.HE Yuyao，YAN Maode.Nonlinear control theory and application[M].Xi’an:Xidian University Press，2007：42-90.(in Chinese)

[8]Kokotovic P，Arcak M.Constructive nonlinear control：a historical perspective[J].Automatica，2001（37）：637-662.

[9]赵连春，杰克·马丁利.飞机发动机控制—设计、系统分析和健康监视[M].北京：航空工业出版社，2011：29-54.Jaw L C，Mattingly J D.Aircraft engine controls design，system analysis，and health monitoring[M].Beijing：Aviation Industry Press，2011：29-54.(in Chinese)

[10]樊思齐，李华聪，樊丁，等.航空发动机控制[M].西安：西北工业大学出版社，2008：81-157.FAN Siqi，LI Huacong，FAN ding，et al.The aeroengine control[M].Xi’an：Northwestern Polytechnical University Press，2008：81-157.(in Chinese)

[11]孙健国，黄金泉，叶志锋，等.现代航空动力装置控制[M].北京：航空工业出版社，2009：140-173.SUN Jianguo，HUANG Jinquan，YE Zhifeng，et al.Modern aircraft power plant control[M].Beijing：Aviation Industry Press，2009：140-173.(in Chinese)

[12]Sugiyama N.Derivation of ABCD system matrices from nonlinear dynamic simulation of jet engines[R].AIAA-92-3319.

[13]陆军，郭迎清，陈小磊.线性拟合法建立航空发动机状态变量模型[J].航空动力学报，2011，26（5）：1172-1177.LU Jun，GUO Yingqing，CHEN Xiaolei.Establishment of aeroengine state variable model based on linear fitting method[J].Journal of Aerospace Power，2011，26（5）：1172-1177.(in Chinese)

[14]冯正平，孙健国，黄金泉，等.一种建立航空发动机状态变量模型的新方法[J].航空动力学报，1998，13（4）：435-438.FENG Zhengping，SUN Jianguo，HUANG Jinquan，et al.A new method for establishing a state variable model of aeroengine [J].Journal of Aerospace Power，1998，13（4）：435-438.(in Chinese)

[15]WANG Jiqiang，YE Zhifeng，HU Zhongzhi.Nonlinear control of aircraft engines using a generalized gronwall-bellman lemma approach[J].Journal of Engineering for Gas Turbines and Power，2012，134（9）：1-6.