双重非对称转子支承系统建模分析方法研究

马威猛，刘永泉，王建军

（1.北京航空航天大学能源与动力工程学院，北京100191；2.中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

转子支承系统的振动特性对旋转机械的工作性能和可靠性具有重要影响，转子系统的振动特性分析一直是工程人员和学者们关注的焦点。现代航空发动机的显著特点是高转速和高推比，转子、支承、机匣之间的动力影响十分紧密[1]，为了准确考虑转、静子之间的耦合振动特性，国内外学者从整机系统的层面对转子支承系统的振动特性进行研究[2-3]，建立同时包含转子和静子系统的整机精细化模型进行分析。但是根据轴对称转子支承系统的分析理论，在实际整机系统建模分析中需对转子系统整体结构或叶片组进行等效简化处理使转子结构满足轴对称要求。该简化降低了系统振动特性分析的精度，甚至有时是不合理的，如具有大型叶片的风扇转子系统。另外，若保留转子和静子的实际结构特征，则从广义上打破了一般转子支承系统建模分析中对转子或静子的轴对称假设，需要从转、静子双重非对称的角度看待转子支承系统整机耦合振动特性分析问题。基于双重非对称转子支承系统结构特点的建模分析理论是解决目前复杂结构转静子耦合系统转子动力学特性分析的关键。

在非对称转子的振动特性分析方面，国内外学者进行的工作各有特点。在国内，王培杰[4]等利用有限元方法对非对称复杂转子进行动力特性分析；肖锡武[5-6]、沈松[7]等研究了非对称转子系统的非线性振动问题；吴敬东等[8-9]对非对称转子系统的碰摩问题进行了深入研究。国内学者对非对称转子的研究更加关注非线性问题，对非对称转子系统的建模分析理论与方法没有给予足够关注。而国外涉及双重非对称转子支承系统的研究虽然较多，但尚未有学者对该类系统的建模方法与分析理论进行系统的整理与评价。

本文整理和介绍了对双重非对称转子支承系统建模分析方法的历史和最新进展，重点阐述了国外学者分析双重非对称转子支承系统时所采用的建模分析方法。

1 双重非对称转子支承系统振动分析的基本问题

本章首先阐述狭义和广义双重非对称转子的概念，然后以狭义双重非对称转子为例说明双重非对称转子支承系统的抽象分析模型和研究的问题。

1.1 狭义和广义双重非对称转子系统

在航空发动机、汽轮机和发电机等旋转机械中，支承系统的结构设计有可能导致转子支点在其支承平面内正交方向上（如竖直和水平方向）具有不同的支承刚度；转子系统因功能设计、装配误差、裂纹故障等原因也可能造成转子截面在平面正交方向上具有不同的弯曲刚度或直径转动惯量。这种支承和转子系统在平面正交方向上同时具有不同刚度或转动惯量特征的系统称作双重非对称转子支承系统[10]，在本文中称为狭义双重非对称转子支承系统。国外相关学者的研究全部基于这个抽象概念，即以明显的转子（刚度、惯量）和支承（刚度）非对称特征定义双重非对称转子支承系统。

现代航空发动机高转速、轻质量、高效率的发展趋势，不断消耗发动机转、静子的“刚性”储备，系统各部件间振动耦合作用突出，在振动特性分析中必须考虑系统结构特征及结构之间的耦合特征[1]。为此，学者提出建立系统高保真结构模型的分析方法，解决轴对称转子与静子支承系统的结构振动耦合分析问题，但若所考虑的转子结构特征不满足轴对称假设，转子的结构模型需要在旋转坐标系描述，而静子支承系统结构模型在静止坐标系描述。如此一来，尽管转子弯曲刚度或转动惯量没有明显的非对称特征，所分析的转、静子耦合系统在分析时也会因动静坐标系的变换在系统整体运动微分方程中引入周期时变系数，具有与狭义双重非对称转子相似的时变特征。本文将这种支承结构具有非对称特征且转子结构不满足轴对称要求的转子支承系统称为广义双重非对称转子支承系统。广义双重非对称转子支承系统的概念放宽了对转子弯曲刚度和转动惯量的非对称要求，工程应用实例十分广泛，又可称为一般转子支承系统。

考虑转子和静子实际结构特征的整机系统转子动力学分析，由于其叶盘转子结构不满足轴对称特征，是1种典型的广义双重非对称转子支承系统，在分析中应该考虑系统的时变特性，并采用相应的时变分析理论进行分析[11]。

1.2 双重非对称转子系统的抽象分析模型

在工程实际中，引起转、静子系统非对称特征的结构形式多种多样，但其本质是一致的，为了便于研究，学者们提出双重非对称转子支承系统的抽象分析模型对系统建模方法和固有振动特性进行研究。在抽象分析模型中，非对称转子支承系统的转子非对称特征在动力学分析中主要表现为正交各向异性的弯曲刚度和直径转动惯量，静子的非对称特征主要表现为正交各向异性的支承刚度和阻尼，典型的双重非对称转子支承系统物理抽象模型如图1所示，非圆截面轴和轮盘分别表征非对称刚度和直径转动惯量特性，坐标平面YZ 上不同的支承刚度和阻尼则代表静子的非对称特征[12]。

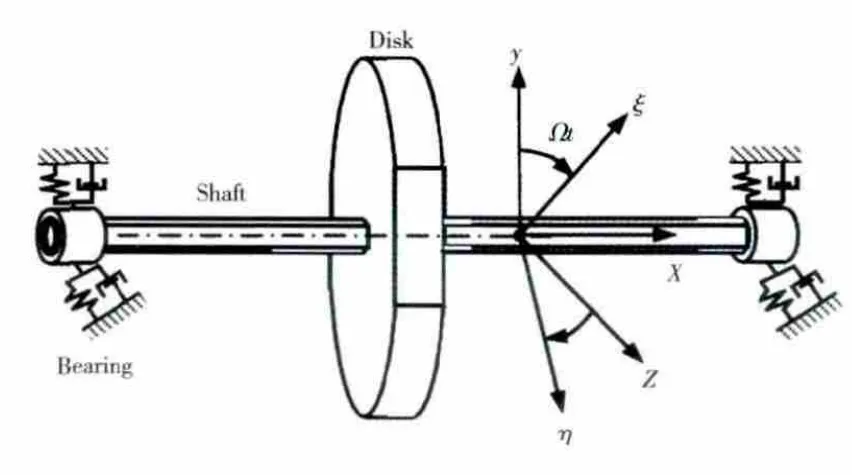
图1 双重非对称转子支承系统模型

1.3 双重非对称转子振动特性分析关注的问题

转子动力学分析主要包括临界转速、稳态响应、瞬态响应和稳定性分析等几方面，双重非对称转子支承系统的分析内容也是类似的几方面，但又具有自身的特点。首先，作为参数振动系统，双重非对称转子支承系统的频率和响应具有多频特性，在临界转速和响应计算中需要注意处理；其次，一般轴对称转子系统的稳定性分析主要由内、外阻尼等因素引起，而双重非对称转子则主要考虑转子自身的非对称特征及其与由其他因素引起的模态失稳[13]。

2 双重非对称转子系统的建模分析方法

本章对国内外学者在研究双重非对称转子支承系统的转子动力学特性过程中提出的大量的理论分析和实验研究方法进行专题介绍。依据计算模型的特点可将上述分析方法大体分为解析法、传递矩阵法、1D有限元法和3D有限元法等。

2.1 解析法

在转子动力学研究的初期，双重非对称转子支承系统即引起了学者们的重视。为了便于研究，学者通常对转子支承系统做较大简化，忽略部分影响因素，以解析的形式对系统的振动特性进行定性分析，其中常用方法为集中质量法和连续结构描述方法。

1943年，Foot[14]在研究双重非对称转子支承系统的临界转速问题时，采用质量点和无质量弹性轴来近似模拟盘和转轴组成的转子支承系统。1961年，Brosens[15]将非对称弹性支承作用下的具有非对称直径转动惯量的转子简化为均布质量的刚体轴和弹簧支承系统进行分析，得到转子截面正交方向上转动自由度的运动方程，发现在超过某转速时，转子会发生动力失稳，而在转速达到一定数值后又恢复稳定的现象。1968年，Black[16]将非对称弹性支承下的非对称弯曲刚度转子简化为单质量无重轴的集中参数模型，基于柔度法推导得到系统平动自由度的运动方程，得到该系统的不稳定边界。集中质量法形式简单，推导方便，受到很多学者的青睐。

解析法的另1种形式是连续结构描述方法，主要用于分析具有均质细长转轴的转子支承系统，基于材料力学的结构理论建立双重非对称转子支承系统的运动微分方程。1969年，Black[17]采用连续梁理论描述具有非对称弯曲刚度的均质等截面轴在非对称刚度支承作用下的振动特性，将转子非对称引起的时变系数项转移到平衡方程右边，作为参数激励项进行考虑。1973年，Iwatsubo[18]基于连续结构体描述，得到与Black类似的运动微分平衡方程，对系统边界条件的选取和积分过程进行了详细说明。

连续结构描述方法与集中参数法相比，虽然在描述部分简单转子支承系统时更加准确，但也具有明显的缺点，如：连续结构描述方法能够描述的转子几何结构非常简单；运动微分方程为4阶，推导及求解过程复杂；一般仅考虑平动自由度，忽略了陀螺效应等转子系统典型特征因素的影响。鉴于此，在双重非对称转子支承系统的基础特性研究中，Gladwell[19]、Yamamoto[20]、Kondo[21-22]、Black[23]、Ota[24-25]等大多数学者采用集中参数法，而只有Bishop[26]、Black[17]、Iwatsubo[18,27]等少数学者采用连续结构描述方法。

解析方法在双重非对称转子支承系统基本特性研究中发挥了重要作用，是学者们早期进行研究的主要方法，但由于采用解析方法需要对系统进行过多简化，不能准确地得到系统的实际响应结果，只能进行定性分析，在其他建模分析方法（如有限元法）发展起来后，解析方法的应用逐渐减少。相对较近的应用，如1996年，Wettergren[28]采用集总质量模型对考虑内部阻尼的非对称支承非对称转子系统的不平衡响应进行研究，以及Ganesan[29]对非对称转子在通过主共振转速时的稳态振动及稳定性的研究。

2.2 传递矩阵法

对于复杂的转子系统，想要获得集中参数描述的分析模型非常困难，甚至是不可能的。因此，通过建立数值计算模型来求解复杂的转子系统。在20世纪60～70年代，计算机的计算能力得到飞速发展，转子动力学分析也从建立解析模型转变为建立描述实际转子几何结构的数值分析模型。针对这种转子模型发展出传递矩阵法和有限元方法。

传递矩阵法是1种重要的转子动力学分析方法，在一般转子动力学分析中应用广泛，在双重非对称转子系统的振动特性分析中应用却很少，这与1D有限元方法在转子动力学分析中的迅速发展有关。传递矩阵方法与转子动力学的1D有限元方法提出的时间间隔较短，在这2种建模分析方法提出之前，学者们主要基于解析方法分析双重非对称转子系统；之后，鉴于有限元方法的优势，学者们更热衷于发展基于1D有限元的双重非对称转子支承系统建模分析方法。

尽管如此，一些学者通过研究，对传统的传递矩阵法进行改进，提出了分析双重非对称转子支承系统振动和响应特性的传递矩阵法。在对微分平衡方程中时变系数的处理上，Inagaki等[30]采用谐波平衡法对转子各段的方程进行谐波展开，得到各阶次谐波系数的平衡方程，并进一步建立对应阶次的传递矩阵表达式进行计算。虽然没有1D有限元法发展的迅速和完善，在双重非对称转子支承系统的振动特性分析中，传递矩阵法也不失为1种可行的建模分析方法。

2.3 1D有限元法

传递矩阵法能够较好地解决一些实际问题，但是在考虑支承系统等转子周围结构时分析较困难，而且可能出现数值不稳定的现象。有限元方法的计算成本比传递矩阵法的要高，但是采用有限元方法便于考虑弹性盘、弹性轴以及弹性支承间的耦合效应。1976年，Nelson等[31]将有限元方法引入到转子动力学分析中，将转子动力学的分析范围和精度提升到一个新的高度。在Nelson等工作的基础上，许多学者对转子动力学的1D有限元分析方法进行补充和完善，基于不同的理论假设，如欧拉-伯努利梁[32]、铁木辛柯梁[33-35]等提出了不同的有限元分析模型来模拟多种形式的转子支承系统在不同工况下的振动行为。

与一般转子支承系统一样，建立非对称转子的有限元方法描述是对双重非对称转子系统进行振动分析的1个关键问题。在1D有限元建模方面，许多学者做出了杰出贡献。1988年，Genta[36]在复坐标框架下建立了基于梁单元、质量、弹簧单元描述的一般非对称转子系统的有限元分析格式，经过简单的坐标变换便可得到转子系统运动方程的固定坐标系及旋转坐标系描述；1996年，Joh[37]根据复模态测试理论，基于方向传递函数dFRF，建立了诊断转子非对称或者支承非对称的测试方法；1997年，Chen和Peng[38]基于有限元方法研究了非对称转子的稳定性问题；2001年，Oncescu[39]等采用有限单元和基于弗洛凯理论的时间转换矩阵相结合的方法推导得到固定坐标系描述的非对称转子的常微分方程，在这些模型中，考虑了转轴的剪切变形，而且考虑了转子截面惯性矩随着轴向方向改变，但没有考虑主惯性矩的惯性主轴方向的变化；2004年，Lee[40]采用坐标变换的方法对非对称转子支承系统进行模态分析，其实质是先采用实坐标建立系统的平衡微分方程，然后对其进行复坐标变换，得到复坐标表达的系统平衡方程并进行求解；2007年，Han[10,41]利用有限元复坐标方法对周期时变系统进行模态分析；2010年，Malta[42]采用最小数量的有限单元离散转子模型，利用弗洛凯理论研究了非对称弹性支承下的非对称转子的稳定性，其中转子转动轴左端和右端的截面惯性主轴方向不同，作者在文中比较了非对称支承和刚性支承下的非对称转子的不稳定区情况，在刚性支承情况下，转子仅有1个不稳定区，而在非对称弹性支承下，转子具有3个间隔的不稳定区。

基于有限元方法对双重非对称转子系统振动特性分析需要解决周期时变矩阵方程的求解问题。许多学者在该方面做了一定的工作，1986年及1990年，Friedmann[43-44]回顾并扩展了求解周期时变微分方程稳定区及线性、非线性响应的数值方法；1991年，Sinha[45]对周期时变微分方程的数值解法进行分析，提出基于Chebyshev行列式展开的方程矩阵表达形式，与基于弗洛凯理论的矩阵展开形式进行比较；而Parszewski[46]在解决非对称转子系统稳定性问题上另辟蹊径，先通过刚性有限元方法计算得到转子与支承的传递函数，然后利用该传递函数进行稳定性分析，大大降低了计算不稳定边界所需矩阵的阶次。

2.4 3D有限元法

1D有限元转子动力学分析方法在考虑剪切效应、盘轴弹性耦合方面存在不足，利用1D有限元方法分析双重非对称转子支承系统时这些不足仍然存在。现代转子动力学分析的发展趋势是考虑转、静子结构耦合特性的整机系统高保真动力学分析。许多学者在转子系统的3D有限元建模分析方法方面做了大量工作，但这些研究中对转子均有轴对称要求，不能准确考虑航空发动机实际的叶盘耦合结构。在此基础上，利用转子动力学3D有限元的分析理论并结合广义双重非对称转子支承系统的概念，对现代旋转机械整机系统进行高保真的转子动力学特性分析具有重要意义。

虽然没有明确提出广义双重非对称转子支承系统的概念，国外一些学者在基于3D有限元的双重非对称转子系统动力学分析方面已经做出了一些尝试。2005年，Nandi[47]在旋转坐标系下建立非对称转子系统的有限元模型，考虑非对称支承，得到在旋转坐标系下描述的线性周期时变微分方程。为了克服周期时变系统引起的稳态求解计算量过大的难题，作者提出1种安排矩阵项的方法，有效利用矩阵的稀疏性，将系统矩阵转换为稀疏矩阵，然后应用稀疏矩阵特征值求解方法求解。需要指出的是，Nandi的分析模型中将支承结构简化为单点弹簧支承，尚未考虑转子与静子实际结构的弹性耦合作用，并且，在旋转坐标系下得到的计算结果不便与实验结果进行对比。2010年，法国学者Lazarus[48]建立了非对称转子系统振动分析的3维有限元模型，提出了分别在转动和静止坐标系建立转、静子模型然后通过转、静子连接关系建立整机耦合系统分析模型（如图2所示）的方法。从图2中可见，Lazarus对转、静子耦合系统的稳定性进行了数值仿真和实验研究。在考虑转子和静子之间的连接关系时，Lazarus仅考虑了转、静子平动自由度的耦合，对此可以开展进一步研究。

图2 Lazarus论文算例研究的转静子耦合系统模型

3 结论

根据上面的讨论，可以归纳上述几种双重非对称转子支承系统建模分析方法的特点：（1）解析法模型简单，易于说明转子支承系统中典型因素对振动特性的影响规律，在定性分析中具有一定优势；（2）传递矩阵法与有限元法的分析过程类似，但不像有限元法那样便于采用通用程序实现；（3）在较好地满足梁单元假设的简单转子系统分析中，1D有限元方法是1种实用便捷的分析方法；（4）3D有限元方法可以对具有复杂结构的转子支承系统进行建模分析，但是目前广义双重非对称转子支承系统的3D有限元分析方法尚需完善。

4 展望

现代航空发动机为代表的旋转机械的发展趋势促进了转子动力学建模分析方法的发展，由集中参数模型到1D简化模型再到3D轴对称模型以及打破转子轴对称要求的广义双重非对称转子支承系统3D建模分析方法，对转子支承系统的建模分析范围和精度不断提升。针对广义双重非对称系统的3D建模分析方法，对进一步需要开展的工作提出几点建议：

（1）完善广义双重非对称系统的3D建模分析技术。除平动振型耦合外，转子的弯曲振型与静子振型在连接位置表现出转角耦合以及其他耦合特征，3D建模分析方法应该至少能够同时考虑平动和转角耦合。

（2）丰富广义双重非对称系统的分析内容及分析方法。广义双重非对称转子系统的非对称特征量较小，其振动特性表现介于狭义双重非对称转子和轴对称转子支承系统之间且具有时变系统的特点，因此需要对广义双重非对称系统进行更多的分析并且分析方法需要适当修正。

（3）建立广义双重非对称系统的分析准则。对工程实际系统的动力学特性分析方法不是越复杂越好。通过采用考虑和不考虑双重非对称特征建模方法的分析结果比较，可以得到转子支承系统何时需要考虑双重非对称的准则，提高实际工程结构动力特性分析的效率。

[1]陈予恕，张华彪.航空发动机整机动力学研究进展与展望[J].航空学报，2011（8）：1371-1391.CHEN Yushu，ZHANG Huabiao.Review and prospect on the research of dynamics of complete aeroengine systems[J].Acta Aeronautica et Astronautica Sinica，2011（8）：1371-1391.（in Chinese）

[2]Chatelet E,D'Ambrosio F,Jacquet-Richardet G.Toward global modelling approaches for dynamic analyses of rotating assemblies of turbomachines[J].Journal of Sound and Vibration，2005，282（1-2）：163-178.

[3]陈萌，马艳红，刘书国，等.航空发动机整机有限元模型转子动力学分析 [J].北京航空航天大学学报，2007，33（9）：1013-1016.CHEN Meng，MA Yanhong,，LIU Shuguo，et al.Rotor-dynamic analysis of whole aeroengine models based on finite element method [J].Journal of Beihang University，2007，33（9）：1013-1016.（in Chinese）

[4]王培杰，滕弘飞，刘笃金，等.非对称复杂转子系统有限元动力分析[J].固体力学学报，1991（4）：370-376.WANG Peijie，TENG Hongfei，LIU Dujin，et al.The dynamic analysis for complex asymmetric rotor-bearing systems by finite element method[J].Acta Mechanica Solida Sinica，1991（4）：370-376.（in Chinese）

[5]肖锡武，肖光华，杨叔子.不对称转子系统的参激强迫振动[J].振动工程学报，2002（3）：71-74.XIAO Xiwu，XIAO Guanghua，YANG Shuzi.Parametrically excited and forced oscillations of an unsymmetrical rotor system[J].Journal of Vibration Engineering，2002（3）：71-74.（in Chinese）

[6]肖锡武，杨正茂，肖光华，等.不对称转子系统的非线性振动[J].华中科技大学学报:自然科学版，2002（5）：81-84.XIAO Xiwu，YANG Zhengmao，XIAO Guanghua，et al.Nonlinear oscillations of an unsymmetrical rotor system[J].Journal of Huzhong University of Science and Technology:Nature Science Edition，2002（5）：81-84.（in Chinese）

[7]沈松，郑兆昌，应怀樵.非对称转子-轴承-基础系统的非线性振动[J].振动与冲击，2004（4）：33-35.SHEN Song，ZHENG Zhaochang，YING Huaiqiao.Nonlinear vibration of unsymmetrical rotor-bearing-foundation system[J].Journal of Vibration and Shock，2004（4）：33-35.（in Chinese）

[8]吴敬东，刘长春，王宗勇，等.非对称转子系统的碰摩运动研究[J].振动工程学报，2006（1）：37-41.WU Jingdong，LIU Changchun，WANG Zongyong，et al.Research on an asymmetrical rotor system with impact-rubbing[J].Journal of Vibration Engineering，2006（1）：37-41.（in Chinese）

[9]吴敬东，刘长春，王宗勇，等.非对称转子-轴承系统碰摩的动力学特性分析[J].振动与冲击，2005（5）：7-10.WU Jingdong，LIU Changchun，WANG Zongyong，et al.Dynamic analysis of asymmetrical rotor-bearing system under the action of rubbing[J].Journal of Vibration and Shock，2005（5）：7-10.（in Chinese）

[10]Lee CW，Han D J，Suh JH，et al.Modal analysis of periodically time-varying linear rotor systems[J].Journal of Sound and Vibration，2007，303（3-5）：553-574.

[11]Kim K T，Lee C W.Dynamic analysis of asymmetric blade drotors supported by anisotropic stator[J].Journal of Sound and Vibration，2012，331（24）：5224-5246.

[12]Lee C W，Han D J，Hong SW.Modal analysis of periodically time-varying linear rotor systems using floquet theory[C]//Proceedings of the 7th IFToMM-Conference on Rotor Dynamics.Austria：International Conference on Rotor Dynamics，2006.

[13]Genta G.Dynamics of rotating systems[M].Germany:Springer,2005：331-346.

[14]Foote W R，Poritsky H，Slade Jr J J.Critical speeds of a rotor with unequal shaft flexibilities,mounted in bearings of unequal flexibilityi[J].Journal of Applied Mechanics-transaitions of the ASME，1943，10：A77-A84.

[15]Brosens P J，Crandall S H.Whirling of unsymmetrical rotors[J].Journal of Applied Mechanics，1961，28（3）：355-362.

[16]Black H F,Mcternan A J.Vibration of a rotating asymmetric shaft supported in asymmetric bearings[J].Journal of Mechanical Engineering Science，1968，10（3）：252-261.

[17]Black H F.Parametrically excited lateral vibrations of an asymmetric slender shaft in asymmetrically flexible bearings[J].Journal of Mechanical Engineering Science，1969，11（1）：57-67.

[18]Iwatsubo T，Tomita A，Kawai R.Vibrations of asymmetric rotors supported by asymmetric bearings[J].Archive of Applied Mechanics，1973，42（6）：416-432.

[19]Gladwell G M L，Stammers C W.On the stability of an unsymmetrical rigid rotor supported in unsymmetrical bearings[J].Journal of Sound and Vibration，1966，3（3）：221-232.

[20]Yamamoto T，Ota H，Kono K.On the unstable vibrations of a shaft with unsymmetrical stiffness carrying an unsymmetrical rotor [J].Journal of Applied Mechanics，1968，35（2）：313-321.

[21]Kondo Y，Okijima K.On the critical speed regions of an asymmetric rotating shaft supported by asymmetrically elastic:1st report,on the unstable regions[J].Bulletin of JSME，1975，18（120）：587-596.

[22]Kondo Y，Okijima K.On the critical speed regions of an asymmetric rotating shaft supported by asymmetrically elastic pedestals:2nd report,on the forced vibrations[J].Bulletin of JSME，1975，18（120）：597-604.

[23]Black H F.The stabilizing capacity of bearings for flex-ible rotors with hysteresis[J].Journal of Engineering for In-dustry，1976，98（1）：87-91.

[24]Ota H，Mizutani K.Influence of unequal pedestal stiffness on the instability regions of a rotating asymmetric shaft[J].Journal of Applied Mechanics，1978,45（2）：400-408.

[25]Ota H，Mizutani K.Influence of unequal pedestal stiffness on the instability regions of a rotating asymmetric shaft:3rd report,mechanism for occurrence of two types of unstable vibrations[J].Bulletin of JSME，1981，24（190）：700-707.

[26]Bishop R E D，Parkinson A G，Bishop R，et al.Second order vibration of flexible shafts[J].Philosophical Transactions of the Royal Society of London.Series A，Mathematical and Physical Sciences，1965，259（1095）：1-31.

[27]Iwatsubo T，Kawai R，Miyaji T.On the stability of a rotating asymmetric shaft supported by asymmetric bearings[J].Bulletin of JSME，1980，23（180）：934-937.

[28]Wettergren H L，Olsson K O.Dynamic instability of a rotating asymmetric shaft with internal viscous damping supported in anisotropic bearings[J].Journal of Sound and Vibration，1996，195（1）：75-84.

[29]Ganesan R.Effects of bearing and shaft asymmetries on the resonant oscillations of a rotor-dynamic system[J].Journal of Engineering for Gas Turbines and Power，1996，118（1）：107-114.

[30]Inagaki T，Kanki H，Shiraki K.Response analysis of a general asymmetric rotor-bearing system[J].Journal of Mechanical Design，1980，102（1）：147-157.

[31]Nelson H D，Mcvaugh J M.The dynamics of rotor-bearing systems using finite elements[J].Journal of Engineering for Industry，1976，98（2）：593-600.

[32]Eshleman R L，Eubanks R A.On the critical speeds of a continuous rotor[J].Journal of Engineering for Industry，1969，91：1180.

[33]Chen L W，Ku D M.Dynamic stability analysis of a rotating shaft by the finite element method[J].Journal of Sound and Vibration，1990，143（1）：143-151.

[34]Chen LW.Ku D M.Finite element analysis of natural whirl speeds of rotating shafts[J].Computers&Structures，1991，40（3）：741-747.

[35]Raffa F A，Vatta F.Gyroscopic effects analysis in the Lagrangian formulation of rotating beams [J].Meccanica，1999，34（5）：357-366.

[36]Genta G.Whirling of unsymmetrical rotors:a finite element approach based on complex coordinates[J].Journal of Sound and Vibration，1988，124（1）：27-53.

[37]Joh C Y，Lee C W.Use of dFRFs for diagnosis of asymmetric/anisotropic properties in rotor-bearing system[J].Journal of Vibration and Acoustics，1996，118（1）：64-69.

[38]Chen L W,Peng W K.Stability analyses of a timo-shenko shaft with dissimilar lateral moments of inertia[J].Journal of Sound and Vibration，1997，207（1）：33-46.

[39]Oncescu F，Lakis A A，Ostiguy G.Investigation of the stability and steady state response of asymmetric rotors，using finite element formulation[J].Journal of Sound and Vibration，2001，245（2）：303-328.

[40]Lee CW，Suh JH，Hong SW.Modal analysis of rotor system using modulated coordinates for asymmetric rotor system with anisotropic stator[C]//8th International Conference on Vibra tions in Rotating Machinery.University of Swansea,UK：Professional Engineering Publishing(Institution of Mechanical Engineers)，2004：575-584.

[41]Han D J.Vibration analysis of periodically time-varying rotor system with transverse crack[J].Mechanical Systems and Signal Processing，2007，21：2857-2879.

[42]Malta J.Stability investigation of anisotropic rotor with different shaft orientation supported by anisotropic bearings：Seminar Nasional Tahunan Teknik Mesin (SNTTM)ke-9[Z].Palembang：2010.

[43]Friedmann P P.Numerical methods for determining the stability and response of periodic systems with applications to helicopter rotor dynamics and aeroelasticity[J].Computers and Mathematics with Applications，1986，12：131-148.

[44]Friedmann P P.Numerical methods for the treatment of periodic systems with applications to structural dynamics and helicopter rotor dynamics[J].Computers&Structures,1990，35（4）：329-347.

[45]Sinha S C，Wu D H.An efficient computational scheme for the analysis of periodic systems[J].Journal of Sound and Vibration，1991，151（1）：91-117.

[46]Parszewski Z A，Krodkiewski J M，Rucinski J.Parametric instabilities of rotor-support systems with asymmetric stiffness and damping matrices[J].Journal of Sound and Vibration，1986，109（1）：111-125.

[47]Nandi A，Neogy S.An efficient scheme for stability analysis of finite element asymmetric rotor models in a rotating frame[J].Finite Elements in Analysis and Design，2005，41（14）：1343-1364.

[48]Lazarus A，Prabel B，Combescure D.A 3d finite element model for the vibration analysis of asymmetric rotating machines[J].Journal of Sound and Vibration，2010,329（18）：3780-3797.