考虑流变效应的高心墙堆石坝应力变形分析
戴吉仙
(中水电海外投资有限公司,北京 100048)
0 引言
近年来,心墙堆石坝以其对地形地质条件极强的适应性而得到了广泛应用。随着国家西部大开发战略的加快实施,我国西部地区正在或即将建设一批调节性能好的高堆石坝。我国在高堆石坝应力变形计算理论与方法等方面取得了阶段性的研究成果。要使堆石坝的预测变形更精确地符合实际变形,必须考虑随时间发展的流变变形[1]。从现有文献资料来看,研究堆石流变性能的方法主要有以下三种:1)将描述弹性、塑性和粘性的理想力学元件进行适当组合形成的流变元件理论模型方法[2];2)通过堆石体的室内流变试验,研究堆石的流变规律[3-5];3)通过对已建面板坝的原型观测资料的反馈分析,从宏观上得出描述堆石体流变的本构模型的拟合参数反馈分析方法[1,6]。本文采用第二种方法得出的流变本构模型,采用三维有限元法计算分析了某高心墙堆石坝的应力变形特征。
1 堆石体本构模型
1.1 静力分析模型
静力分析模型采用邓肯E-B 非线性弹性模型[7],该模型概念明确,所需试验简单易行,在土石坝的变形计算分析中得到了非常广泛的应用。
切线模量的表达式为:

其中,c 为材料凝聚力;φ 为内摩擦角;Rf为破坏比;k 为模型参数切线模量基数;n 为切线模量指数;pa为单位大气压力。
卸载时切线弹模Eur随着侧限压强σ3而变化,可以用式(2)计算:

其中,Kur,nur均为由试验确定的两个系数。
切线体积模量为:

其中,Kb为体积模量系数;m 为体积模量指数。
模型同时还考虑粗粒料内摩擦角φ 随围压σ3的变化:
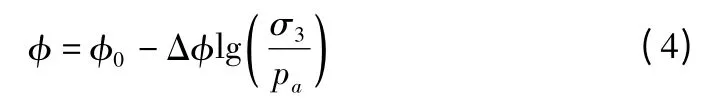
其中,φ0为σ3等于单位大气压力时的φ 值;Δφ 为反映φ 值随σ3而降低的一个参数。
1.2 流变分析模型
本文流变分析模型采用以指数型衰减的Merchant 模型[4,5],流变变形可表达为:

其中,εf为最终流变量;α 为流变随时间衰减的指数。
对式(5)求导并将应变分解为体积应变和剪切应变两个部分:

其中,εvf,γf分别为最终体积流变和最终剪切流变;εvt,γt分别为t 时刻体积流变和剪切流变的累加值。
最终体积流变和剪切流变采用式(8):

其中,β,b,mc,nc,d,lc均为模型参数;q 为偏应力;Sl为应力水平。
堆石体的流变特性可以由式(5),式(8)描述,该模型包括α,β,b,mc,nc,d,lc七个参数。
2 工程实例分析
2.1 工程概况与模型信息
某土质心墙堆石坝最大坝高约314 m。电站水库正常蓄水位2 500 m,水库总库容约为29 亿m3,具有年调节能力,电站装机容量2 000 MW。坝址区河谷属高山深切曲流河谷,谷坡陡峻;河床覆盖层深厚。大坝为目前国内设计和拟建的最高土石坝,鉴于此,本文以该大坝作为研究对象,对高心墙堆石坝的应力变形进行分析。
大坝的三维有限元网格剖分如图1 所示,本次计算完全模拟了心墙堆石坝整个坝体以及坝基,剖分时主要采用8 结点6 面体单元,为适应边界过渡,采用了部分棱柱体单元。流变模型材料参数见表1。

表1 心墙堆石坝流变模型材料参数
2.2 成果分析
图2~图5 为典型断面考虑了流变效应的基本稳定期的变形和应力结果。在流变效应的作用下,堆石坝体的应力、变形会发生重分布。大坝变形基本稳定期的坝体沉降为3.36 m,约为坝高的1.07%,位置约为1/2 坝高处;坝体最大水平位移发生在心墙中上部,为91.48 cm。基本稳定期堆石体大主应力极值和小主应力极值分别为4.29 MPa 和1.65 MPa,上游堆石的大主应力小于下游侧的大主应力。堆石体的流变变形将引起堆石体应力的调整,使得堆石体趋于更加密实,应力趋向更加均匀,但由于心墙土料较软,在堆石与心墙之间存在变形不协调现象,心墙仍存在一定的拱效应,如图4 所示。

图1 大坝三维有限元网格图

图2 典型断面考虑流变效应基本稳定期铅直位移等值线图(单位:cm)
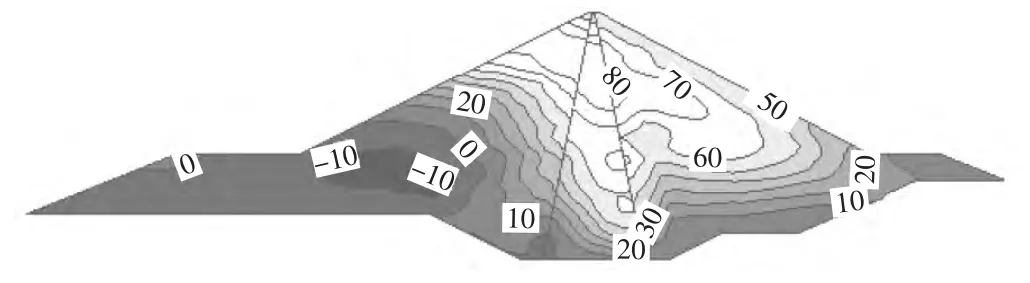
图3 典型断面考虑流变效应基本稳定期水平位移等值线图(单位:cm)

图4 典型断面考虑流变效应基本稳定期大主应力等值线图(单位:MPa)
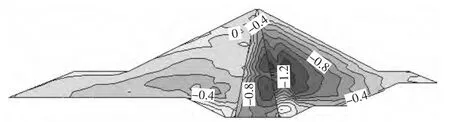
图5 典型断面考虑流变效应基本稳定期小主应力等值线图(单位:MPa)
大坝的应力变形值在合理范围内。与类似工程相比,该心墙堆石坝的位移及应力分布符合心墙堆石坝应力变形的一般性规律。考虑流变效应的心墙堆石坝应力变形最大值见表2。
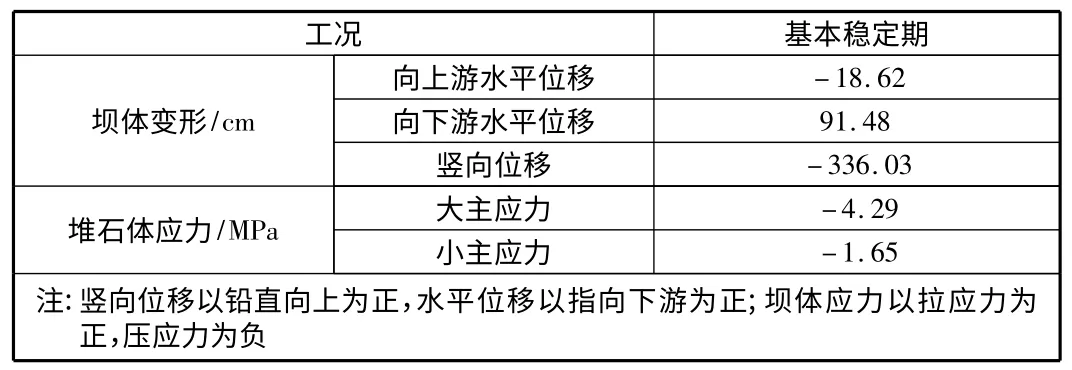
表2 考虑流变效应的心墙堆石坝应力变形最大值
3 结语
采用考虑流变效应的三维有限元法对某高心墙堆石坝的应力变形进行了计算分析,大坝的应力变形值在合理范围内,基本稳定期的坝体沉降约占坝高的1.07%,坝体水平位移基本指向下游,心墙存在一定的拱效应。该心墙堆石坝的位移及应力分布符合心墙堆石坝应力变形的一般规律。
[1]沈珠江.鲁布革心墙堆石坝变形的反馈分析[J].岩土工程学报,1994,16(3) :1-13.
[2]蒋国澄,赵增凯.中国的高混凝土面板堆石坝[A].混凝土面板堆石坝国际研讨会论文集[C].2000.
[3]王 勇,殷宗泽.一个用于面板坝流变分析的堆石流变模型[J].岩土力学,2000,21(3) :227-230.
[4]沈珠江.土石料的流变模型及其应用[J].水利水运科学研究,1994(4) :335-342.
[5]沈珠江,左元明.堆石料的流变特性试验研究[A].第六届土力学及基础工程学术会议论文集[C].1991:443-446.
[6]张丙印,袁会娜,李全明.基于神经网络和演化算法的土石坝位移反演分析[J].岩土力学,2005,26(4) :547-552.
[7]钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,2000.

