OFDMA系统中基于多业务QoS保证的机会调度算法
张冬梅 马文峰 益晓新 徐友云
(解放军理工大学通信工程学院,南京,210007)
引 言
正交频分多址接入(Orthogonal frequency division multiple access,OFDMA)系统作为第四代移动通信标准,一个重要特征是能利用无线资源分配技术来为用户提供业务服务质量(Quality of service,QoS)的保证,在无线资源分配时如何实现业务QoS保证和系统资源利用率间的平衡一直是学术研究热点。研究场景包括多用户单业务[1-3]、多用户多业务[4-5]、协同[6]、组播[7]等,涉及的资源包括子载波、功率、自适应调制、比特、天线、中继等资源,所有这些资源的联合优化是一个复杂度极高的问题,实际研究时均采用分步优化的方法,其中子载波分配是OFDMA系统资源分配的基础。如文献[3]研究在高速移动环境多业务场景下根据业务的误比特率(Bit error rate,BER)将子载波按簇分配给用户问题;文献[5]在假设系统完成用户子载波随机分配的基础上研究各子载波上的功率分配问题;文献[7]在组播OFDMA系统中先将子载波分配给各用户组,再实现各子载波的功率和比特分配。本文讨论多用户多业务场景下的基于QoS保证的子载波分配问题。
在无线系统中由于信道的多变性,增加了资源分配的复杂度,但同时在资源分配中也可利用无线信道的多变性来提高频谱效率,这就是机会调度[8]。从优化系统总吞吐量的目标出发,最优结果是在每个时刻调度信道状态最好的用户。这种思想也可以应用于OFDMA系统,即贪婪算法,以系统总吞吐量最大为目标,每个子载波分配给信道状态最好的用户。但在这种情况下,尽管系统吞吐量达到最大值,却完全不考虑用户公平性和QoS要求,这与实际系统要求是不相符的。文献[8]中提出了3种基于不同QoS要求的机会调度策略,即基于资源公平共享、基于性能公平和基于各用户的最小性能保证的3种QoS要求。
目前,关于OFDMA系统中子载波分配算法的研究都是为了实现一种或几种系统QoS指标,本文主要借鉴文献[2]的研究思路利用图论中的最大加权双向匹配问题的求解方法,研究多业务场景下基于QoS性能保证的子载波资源调度问题。文献[2]讨论了系统中用户数小于子载波数,所有用户的业务类型为单一的非实时业务时机会调度策略的实现及效果。从文献中仿真结果可看出,系统的总吞吐量确实比轮询(Round robin,RR)算法时有明显提高,但各用户间的公平性能并不理想,只是比Greedy算法有了一定程度的改进。由于非实时业务本身对用户吞吐量的保证和公平要求并不太高,因此文献[2]中的控制参量设置能满足非实时业务需求,但对于实时业务的调度就不合适了。本文讨论基于多种业务包括实时业务QoS性能保证的公平调度算法,并给出了仿真结果和性能评估。仿真证实通过合理设置控制参量,这种算法在多业务条件下能为各业务提供QoS保证,体现了业务间的公平性,同时明显增加系统总吞吐量。
1 系统模型
在OFDMA系统中,一个小区的下行链路上多个用户的资源分配如图1所示。在基站侧,所有下行链路分组在基站排队,资源调度器有下行排队状态的完全信息。同时,所有移动用户关于信道的状态信息通过反馈信道传送到资源调度器。资源调度器根据信道状态和各下行数据流排队状况,做出子载波和功率分配策略,并传送给OFDM收发信机。OFDM收发信机根据子载波分配情况,从不同用户队列中取出数据形成一个OFDM符号,按确定的功率发射出去。这里,假设移动用户对信道状态的估计是准确的,并且瞬时信道状态信息是可用的,每个子载波在一个时隙内只分给一个用户,资源分配策略更新与信道信息收集是同步的,同时资源分配信息通过分离的控制信道传输给移动台。

图1 OFDMA系统模型Fig.1 OFDMA system model
2 多业务条件下的机会调度算法
公平性是无线系统调度问题的核心。没有好的公平准则,可能会出现某些用户得不到系统资源的情况,此时的优化没有价值。好的调度策略要能利用用户的不同时变信道条件,在保证用户间的某种公平性能的同时,实现无线资源的高利用率。传统机会调度的思路是最大化系统总吞吐量,本文重点讨论基于多业务QoS保证前提下,使系统总吞吐量尽量大的调度问题。
2.1 调度问题的公式化描述
本文讨论的机会公平调度主要考虑用户吞吐量和系统总吞吐量。
第t时隙时,用户k在第n子载波上的吞吐量为

式中:k=1,2,…,K为用户编号;n=1,2,…,N为子载波编号;t=1,2,…,T为时隙编号;B为系统带宽;N为子载波个数;,为第t时隙时用户k在第n个子载波上的信道增益和发送功率;N0表示加性噪声的单边功率谱;Γ表示与物理层编码调制关联的冗余量,不考虑传输的误码率和物理层编码调制时Γ=1,此时容量为香农容量。考虑传输的误码率为BER和物理层编码调制方式为MQAM与格雷编码联合[9]时,Γ=-ln(5BER)/1.5。
用户k在T个时隙内的平均吞吐量为

式中:π为子载波调度的某一确定方案,π(ω)={π(ω1),π(ω2),…,π(ωt),…}∈Π,Π为所有调度方案的集合,π(ωt)=At为t时隙时的一种调度方案,π*(ωt)为t时隙时的最优调度方案;At=为t时隙占用各子载波的用户序号矢量;1{Atn=k}的取值为1或0,1{Atn=k}=1时表示第t时隙时第n子载波分配给用户k,1{Atn=k}=0时表示第t时隙时第n子载波未分配给用户k。
因此,系统的平均吞吐量为
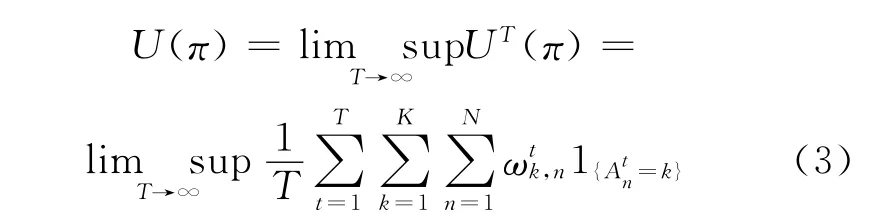
下面分析业务最小性能保证(Minimum performance guarantee,MPG)的调度问题。
在实际系统中对于一个确定的用户,考虑更多的是对其业务QoS指标的保证,因此在资源分配中应考虑分配后各用户所能达到的吞吐量是否满足业务需求,这就是基于保证每个用户的最小性能(吞吐量)的机会调度问题。其描述为

式中:C= {C1,C2,…,CK}表示各用户在T个时隙内要求的最小吞吐量指标。
式(4)的求解可以利用各种优化方法来实现,但在找到某个π时,还有同时满足约束条件(π)≥Ck。最优解的获得将是一个多次迭代运算的过程。其最优解为

式中,为最优解的控制参量,其设定原则为
W(1)≥1;
W(2)lim infT→∞(π)>Ck;
W(3)若lim infT→∞(π)>Ck,则=1。
2.2 基于图论的优化求解算法
这种调度问题可以表示为图论中的二分图问题(K,N,Π,ω),K表示用户集合,N表示子载波集合,Π表示将所有子载波分配给用户的所有调度方案集合,ω为每种调度方案的加权值,即此时的用户吞吐量。最优调度方案的求解,就是在K与N集合元素配对中寻找加权值和为最大的调度方案π,即最大加权双向匹配问题[2]。
最大加权双向匹配问题的最优解求解算法是Hungarian算法[10],其主要步骤:
(1)以各用户各子载波上的加权值为基础构造出N×N的代价矩阵,每个用户分解为个子用户,每个子用户只能分配一个子载波。
(2)进行矩阵变换,每行(列)分别减去本行(列)的最小值得到一个与原代价矩阵同解的新矩阵。
(3)寻找新矩阵的独立零元素组,当独立零元素组中元素个数为N,就已求出最优解。否则重复步骤(2)继续进行矩阵变换。
(4)根据独立零元素的位置,将子载波分配给相应的用户。Hungarian算法的复杂度较高,为Ο(max(N,K)3)。
文献[2]采用一种次优的max-max算法,其主要思想是选取整个代价矩阵中最大元素,分配相应子载波给用户,删除相关行列,形成新的代价矩阵,再求最大元素,逐一分配子载波,直至分完为止。该算法的复杂度为Ο(N)+Ο(K),明显低于Hungarian算法,而两种算法的吞吐量性能相差不大。在本文仿真中只采用次优的max-max算法。
2.3 多业务的公平算法
在将机会公平调度问题转化为最大加权双向匹配问题后,可利用成熟的Hungarian算法和max-max算法,求出其最优解和次优解。但此时在求解中还有一个核心问题需要解决,这就是控制参量的设置。
在文献[2]中研究了系统中用户数小于子载波数,所有用户的业务类型为单一的非实时业务时机会公平调度策略的实现及效果。从文献中的仿真结果可看出,系统的总吞吐量确实比轮询算法时有明显提高,但各用户间的公平性能并不理想,只是比贪婪算法有了一定程度的改进。由于非实时业务本身对用户吞吐量的保证和公平要求并不太高,因此文献中的控制参量设置是能满足非实时业务需求的。但对于实时业务的调度就不合适了。
在式(5)描述的调度策略中要求预先确定各用户所要求的最小吞吐量,从考虑业务QoS要求角度出发,可根据用户业务的速率、时延等QoS指标来确定用户所要求的最小吞吐量。从考虑不同业务间的公平性能性角度考虑,本文采用归一化加权参数ρk来表示用户k业务占用的系统资源的比例

式中:Rk为用户k所要求业务速率为所有业务中要求速率最低的业务速率;ρk为用户k业务的归一化速率要求,表示其所需的资源份数;当用户业务所要求QoS指标越高,其ρk值越大,要求占用系统的资源将越多。
为了便于分析算法性能,在算法仿真时,假设同等条件时轮询算法的平均吞吐量就是最低级别用户所要求的吞吐量c0
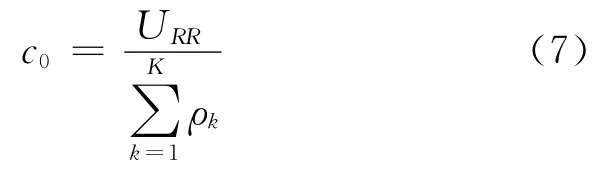
式中:URR为采用轮询算法时的系统总吞吐量,为所有用户所需资源的总份数,则各用户的最小吞吐量指标Ck=ρk·c0。
对于寻根问题f(x*)=0,在f(x)是凸函数的前提下,如果能根据任一x值求出f(x),则可以利用以下迭代算法求出x*

式中:δi为迭代步长,决定迭代算法的收敛速度,其值越大,xi越快接近x*,但取值波动较大。
控制参量的设置同样也可利用寻根问题的迭代求解方法,根据式(4,5)定义
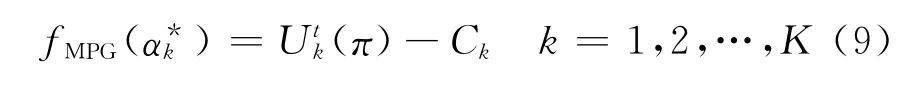

在调度开始时将控制参量设为=1,以后每次调度前先重新设置控制参量。若(π)>Ck,则=1,否则按式(10)进行设置。
3 仿真与分析
本文采用经典的Greedy算法和RR算法作为边界算法,重点分析不同步长对MPG算法在系统资源利用率和业务QoS保证上的性能差异。
为了分析算法性能,本文定义两个性能参量:系统吞吐量增益G和用户最小性能比例PMPG。
系统吞吐量增益G是以同等条件下采用RR算法时的系统吞吐量URR为基准,计算公式为
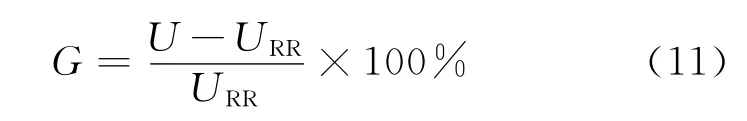
式中:G表示算法的系统资源利用性能,具有机会调度特性的算法的G>0,G越大表示系统资源利用率越高,Greedy算法的G值为上界。
用户最小性能比例PMPG以同等条件时RR算法的平均吞吐量c0为基准,计算公式为
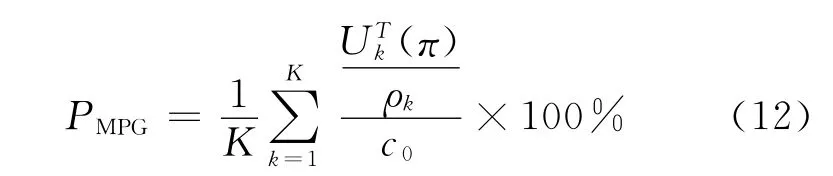
式中:PMPG表示算法的业务QoS保证性能,体现业务间的公平性。PMPG的取值范围为 (0 ,100],PMPG=100表示相同优先级的用户获得了相同的吞吐量,不同优先级用户获得的吞吐量与优先级成正比,即算法保证了业务的QoS。PMPG越小表示用户间公平性越差。
在仿真中,考虑单小区的OFDMA系统的下行链路数据传输,系统带宽为4MHz,划分为256个子载波。假设用户在小区中均匀分布,所有用户根据与基站的距离分为近距、中距和远距3种,其分布比例为1∶2∶1,仿真时设置用户1为近距用户、用户2和用户3为中距用户、用户4为远距用户,其他用户类型按此规律设置。相同类型用户的平均SNR一致,不同类型用户的平均SNR的最大差值为10dB。无线信道模型采用COST207中的城区模型,由6条瑞利信道组成的频率非选择性衰落信道,时延扩展γ=2.5μs,每个子载波对应的信道为平坦衰落信道[11]。本文只研究子载波调度问题,仿真中同一用户占用多个子载波时,子载波间采用平均分配功率。为了便于说明,仿真中假设系统有3种业务,误码率均为10-3,各类业务加权参数ρ=1,2,4,各类业务用户出现的概率分别为0.5,0.25,0.25,各用户的业务类型是在仿真中随机产生的。
MPG1算法的步长δt=1;MPG2算法的步长的步长算法的步长同时在算法实现预置c0时,使c0略大于标准值,MPG4算法是对MPG2算法的修正。
图2给出了4种MPG算法的系统吞吐量增益曲线对比。图中,横坐标为系统中用户数,用K表示,纵坐标为系统吞吐量增益,用G表示。其中Greedy算法的系统吞吐量增益曲线作为性能的上界。

图2 MPG算法的系统吞吐量增益比较Fig.2 System throughput gain of MPG algorithms
图3给出了4种MPG算法实际最小性能的对比曲线,图中,横坐标为系统中用户数,纵坐标为用户最小性能比例PMPG。
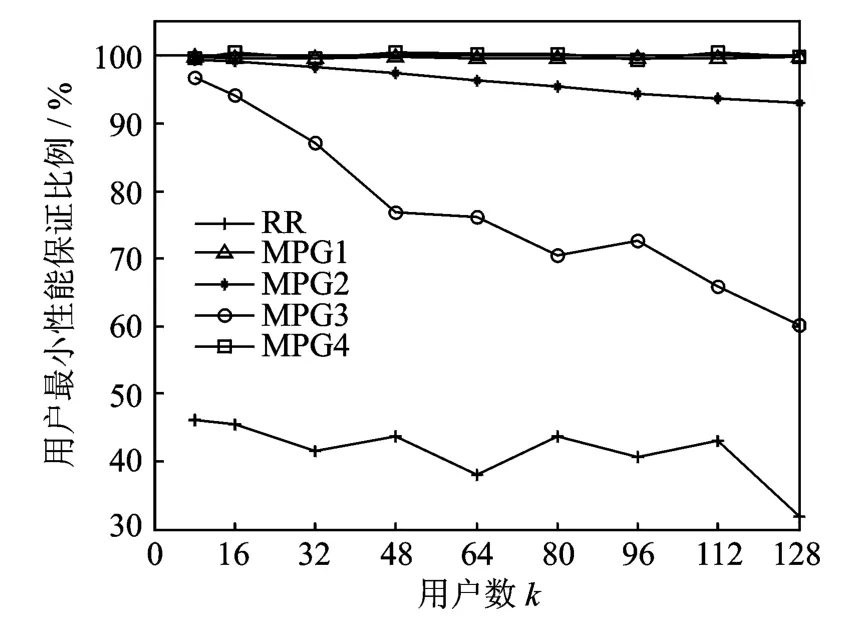
图3 MPG算法的用户最小性能比例参数比较Fig.3 Ratio parameter of user minimum-performance in MPG algorithms
从两图可看出:MPG1算法能完全满足算法的约束条件,但系统吞吐量的增益不太大;MPG3算法能明显提高系统吞吐量,但对最小性能的保证明显不够;MPG2算法在提高系统吞吐量的同时,对最小性能的保证也偏差不大;MPG4算法通过设置合理c0值,在保证系统系统吞吐量增益的同时保证了对最小性能的保证,由此可知是MPG算法时较理想的选择。4种MPG算法的差异就是步长的取值不同,总的算法复杂度是完全相同的。
4 结束语
本文研究了在多业务条件下以保证各用户业务最小性能为目标的资源调度算法的实现方法,并进行了计算机仿真。结果表明,通过合理设置控制参量,该算法在多业务条件下为系统提供不同业务间的公平保证,并明显增加系统总吞吐量。当然,本文的研究前提是调度器可获得完全的信道状态信息,这是一种理想假设,下一步将研究在有限反馈条件下机会公平调度算法的实现。另外,本文所采用的QoS指标是最常用的业务数据速率来设计子载波调度参数,下一步将考虑综合利用QoS其他参数如时延和超时概率等来定义用户业务加权参数,使算法更接近实际应用。
[1]Wong C Y,Cheng R S,Letaief K B,et al.Multiuser OFDM with adaptive subcarrier,bit,and power allocation[J].IEEE Journal on Selected Areas in Communications,1999,17(10):1747-1768.
[2]Zhang Z,He Y,Chong E K P.Opportunistic downlink scheduling for multiuser OFDM systems[C]∥Wireless Communications and Networking Conference.New Orleans:Proceeding of IEEE WCNC,2005:1206-1212.
[3]Zhu H.Radio resource allocation for OFDMA systems in high speed environments[J].IEEE Journal on Selected Areas in Communications,2012,30(4):748-758.
[4]Hassan N UL,Assaad M.Time scheduling subcarrier and power allocation in multi-service downlink OFDMA Systems[C]∥International Conference on Communications.South Africa:IEEE ICC,2010:1-6.
[5]陈松,郑娜娥,王大鸣,等.基于QOE效用函数的多用户OFDM系统功率分配算法 [J].数据采集与处理,2011,26(6):648-653.Chen Song,Zheng Na e,Wang Daming,et al.QOE utility function-based power allocation algorithm in multiuser OFDM systems[J].Journal of Data Acquisition and Processing,2011,26(6):648-653.
[6]蔡春晓,蔡跃明,杨文东.协同OFDM系统联合中继选择、子载波配对和功率分配算法 [J].数据采集与处理,2011,26(3):275-279.Cai Chunxiao,Cai Yueming,Yang Wendong.Joint of relay selection,subcarrier pairing and power allocation for cooperative OFDM systems[J].Journal of Data Acquisition and Processing,2011,26(3):275-279.
[7]Kagan B,Wu M Q,Liu H,et al.Adaptive resource allocation in multicast OFDMA systems[C]∥ Wireless Communications and Networking Conference.Australia:IEEE,2010:18-26.
[8]Liu X,Chong E,Shroff N B.A framework for opportunistic scheduling in wireless networks [J].Computer Networks,2003,41(4):451-474.
[9]Goldsmith A J,Chua S G.Variable-rate variablepower MQAM for fading channels [J].IEEE Transacation on Communication,1997,45(10):1218-1230.
[10]Kuhn H W.The Hungarian method for the assignment problem [J].Naval Research Logistics Quarterly,1955(2):83-97.
[11]杨大成.移动传播环境[M].北京:机械工业出版社,2003.Yang Dacheng.Mobile communication environment[M].Beijing:China Machine Press,2003.

