考虑电动汽车接入的配电系统静态电压稳定裕度研究
郑 颖 孙近文 张 冲 林湘宁
(1. 华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074 2. 广州供电局有限公司 广州 510620)
1 引言
随着经济发展、社会能源供给与环境保护之间的矛盾的日益加剧,节能降耗和减少对化石燃料的依赖已经成为经济可持续发展迫切需要解决的问题。电动汽车(Electric Vehicle, EV)作为解决交通、能源和环境问题的重要手段,能够较大地缓解上述矛盾,为整个社会的可持续发展奠定良好基础。然而,大规模电动汽车的应用势必给电网带来一定影响,在电动汽车用户较为集中的配电系统内,由于附属充电设施的建设可能超出配电系统设计预期,会对其接入的配电系统的运行安稳水平构成严峻威胁。鉴于大多数用户对于电网电压的敏感性,配电系统的电压稳定问题[1]将是制约电动汽车能否规模化应用的重要因素[2]。尽管电压稳定问题的研究目前较多体现在输电网层面,不少文献也提出了在配电网出现电压失稳甚至崩溃的情景[3-7],如见诸报道的 1997年巴西某电网配电网电压失稳事故[8]。
文献[9]提出了配电系统电压失稳主要成因是负荷需求的增长超出设备运行的极限状态,系统不能维持负荷功率与负荷所吸收功率之间的平衡,越过其临界点。电动汽车的大规模推广将会使用电负荷和用电量急剧增长,其带来的负荷率不断降低,这必将成为将来配网系统电压水平恶化甚至崩溃的重要诱因[10]。文献[11-14]则论述了新能源大规模接入配电系统后电网电压稳定性的判断与优化策略。上述研究虽然已经做了较多的工作,但对于配电网络接纳电动汽车的方式及运行场景论述尚不够全面,相应的紧急控制策略及效果亦鲜有论及,而本文的工作正是建立在这些研究空白之上。
电动汽车对于电网稳定性影响的特殊性还体现在其充电行为在时空上的随机性,同时也使其充电需求具备一定的灵活性。这就要求在研究电动汽车高功率接入配电系统对电压稳定性的影响之前,必须厘清电动汽车的静态负荷特性。目前对含电动汽车的配网静态方面研究已经取得了丰富的进展,主要集中在负荷分布及有序调控、压降分布和配网损耗等方面。文献[15, 16]分析了不同类型电动汽车的不同充电行为对应的充电方式及充电时段,并根据不同类型电动汽车不同充电行为的充电功率,获得电动汽车充电负荷规律。文献[17]研究了电动汽车充电对配电网负荷曲线、网络线损及节点电压偏移的影响,并考虑了以负荷方差最小化为目标的优化充电策略。文献[18]结合美国电网实际运行数据和道路交通情报,构建了电动汽车充电规律对配电网的影响模型。文献[19]采用蒙特卡洛仿真研究了电动汽车在不同普及程度、电价条件和季节下对配电系统网损率和电压偏移的影响。
本文以某电力公司实测电动汽车示范工程充电数据为基础,得出了其拟合五阶高斯充电分布特性,在此基础上分析了采用无序充电和优化调控充电方式时,不同渗透率的电动汽车充电对配电系统电压稳定裕度造成的不同程度的影响,以及电动汽车以不同比例接入充电站节点及分散充电时对配电系统电压稳定裕度的影响,分析了配电网电压稳定与上述因素的关系,最后依据系统电压稳定裕度设计了切负荷紧急控制策略,以提高系统应对电压失稳的能力。
2 规模化EV接入后的配电系统电压稳定模型
2.1 电动汽车负荷模型及计算方法
电动汽车充电行为是影响电动汽车功率需求的关键因素。其随机性依赖于充电时间、地点、频率以及日行驶里程。其中充电开始时刻受行驶结束时刻影响。对于每一辆电动汽车,其充电需求模拟的基本思路是先根据日行驶里程概率密度分布函数式产生日行驶里程,然后根据汽车百公里耗能得到充电能量需求值。日行驶里程[19]反映了电动汽车一天内消耗的电能,并近似满足对数正态分布
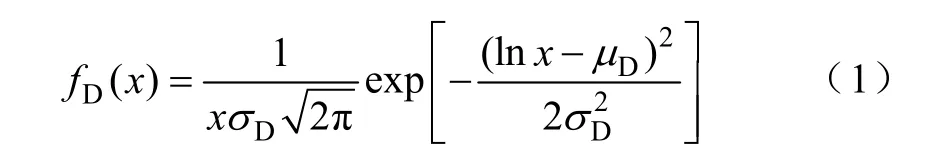
式中,x表示电动汽车日行驶距离;σD表示对数正态分布的方差;μD表示对数正态分布的期望。
根据山东电力集团公司统计数据,典型负荷日中,电动汽车充电开始时刻的概率密度服从五阶高斯分布,如图1所示。
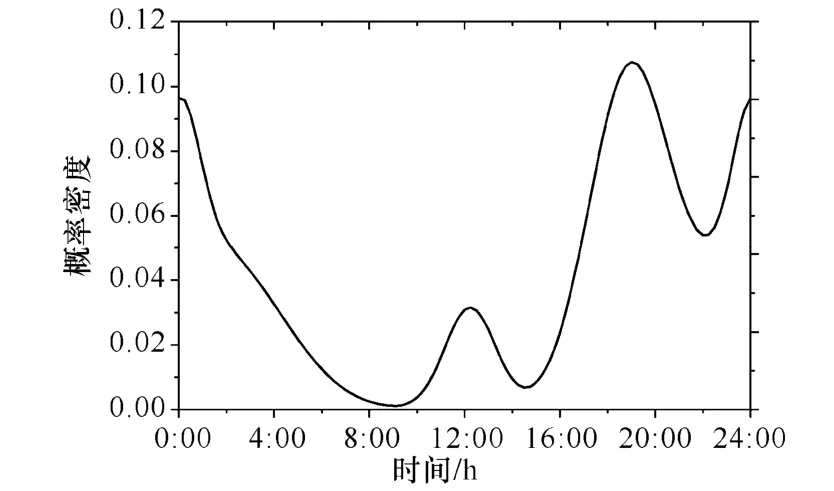
图1 充电开始时刻概率密度Fig.1 The probability density of charging time
根据图1,充电开始时刻满足分布
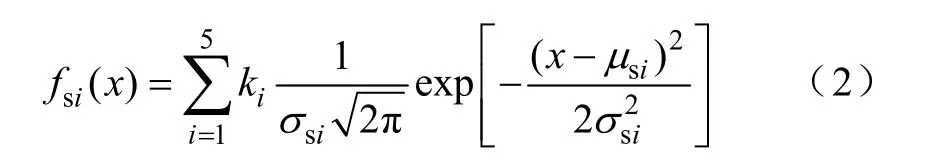
式中,x表示电动汽车充电开始时刻;σsi、μsi分别为分布的方差和期望;ki为每一个分布的权重系数。σsi、μsi、ki的值具体见表 1。

表1 充电开始时刻概率密度参数设置Tab.1 Parameter settings of the probability density of charging time
表 2给出了MIT[20]、USABC和 EPRI[21]研究的几种典型电动汽车的电池特性,其中PHEV X中的X表示该电动汽车能够行驶的最大里程(以 mile计)。其中,充电功率的大小同时取决于电池特性以及充电方式。

表2 几种典型电动汽车充电特性Tab.2 Charging load profile of several typical kinds of EVs
本文考虑两种用户充电情况:①在无经济利益和政策引导的情况下,电动汽车的充电行为服从其自然分布规律,充电开始时刻根据分布函数式(2)随机选取。②考虑利用峰谷分时充电电价策略对充电行为进行调控,检验其是否可以起到很好的效果。峰谷分时充电电价策略见文献[22]。假设 90%
的电动汽车选择谷电价时段充电,余下部分随机选择充电时间,即η=0.9。谷电价时段为1:00~7:00,
则建立最优化模型为
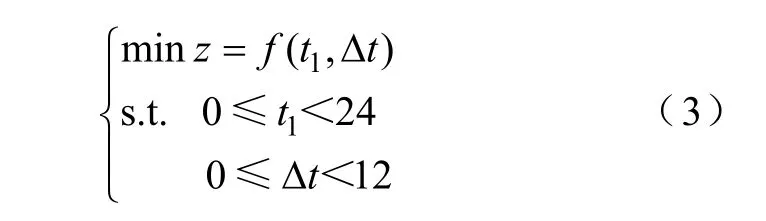
考虑PHEV 30、PHEV 40和PHEV 60三种电动汽车类型,其比例为70%、12%和18%,且95%的电动汽车采用正常充电,5%的电动汽车采用快速充电[23]。考虑到夜间电动汽车大多分散在各节点充电,假设 7:00~24:00期间,比例为 α的电动汽车接入充电站规划节点,余下1-α部分随机接入其他节点,而 0:00~7:00期间,10%的电动汽车接入充电站规划节点,90%的电动汽车随机接入其他节点。
根据以上假设,可以确定电动汽车充电开始时刻及电动汽车充电所需要的电能;再结合电动汽车充电特性,通过以下过程得到每辆电动汽车的充电负荷曲线:
(1)确定电动汽车类型及充电方式,根据电动汽车日行驶里程分布函数式随机产生电动汽车的日行驶里程。
(2)确定电动汽车充电时刻,选取电动汽车充电接入点。根据前面的假设和分析,电动汽车充电时刻有两种可能:①根据分布函数式(2)随机产生电动汽车充电开始时刻;②汽车在峰谷分时充电电价策略调控下充电。电动汽车接入点也有两种可能:①随机选取充电站节点接入;②随机选取所有负荷节点接入。
2.2 连续潮流法追踪PV曲线
在电压稳定的研究方法中,PV曲线作为较为传统的动态分析法可以准确求取任意系统电压稳定的功率极限值和电压临界值,因此具有普适意义。系统的潮流方程可用式(4)表示。式中,λ为负荷增长率;b为负荷增长方式。

连续潮流法[24]在系统准稳态条件下不断求解潮流方程,从而描绘出系统电压随负荷的缓慢增加的规律,即PV曲线。常规潮流沿着PV曲线逐点收敛,但在接近临界点处,系统方程各变量的一阶偏导几乎为零,从而导致雅可比矩阵奇异。因此,只要对潮流收敛方向进行适当调整,即对潮流方向进行合理预报,并添加第N+1维方程,构造N+1维空间,就能避免上述问题。
本文选取弧长公式为第N+1维方程,从而得到系统的改进潮流方程为

式中,x0为潮流解的电压值;λ0为负荷增长率。
在追踪 PV曲线过程中引用预估校正技术,能加快运算速度。预估方法采用切线法,得到下一个潮流解的预估值,再通过潮流方程进行校正。
PV曲线追踪过程中有多种负荷增长方式,本文选取按各节点之间原负荷比例以及各节点原有功与无功负荷比例方式增长负荷。
对某一节点进行 PV曲线追踪,得到功率极限点的负荷增长率为λmax,定义电压稳定裕度为

3 含电动汽车配电系统电压稳定分析
选取图2所示IEEE 34节点配电系统进行分析,配网最大负荷容量为4 944kW。其中节点824、840、858为充电站节点,节点800为平衡节点,出力不受限制。

图2 IEEE 34节点系统Fig.2 IEEE 34 system
文献[17, 19]都分析了不同渗透率下PHEV分别采用多种充电方式时对配网网损及节点电压偏移的影响,并假设电动汽车随机接入系统各个节点,文献[25]分析了不同优化目标下电动汽车对电网的影响,并假设电动汽车负荷均接在59节点,这些研究均未考虑充电站与分散充电并存的实际情况。本文假设配网中有三个充电站节点,一定比例的电动汽车随机接入其中任一节点,余下部分随机接入其他节点。
由于受电动汽车类型及充电方式的影响,实际接入的电动汽车功率需要通过分析计算得到。定义渗透率rp为

式中,PEV为无序接入电网的电动汽车负荷峰值。
先根据前文方法产生各节点的电动汽车充电负荷曲线及常规负荷曲线,然后生成各节点的净负荷曲线。对配网采用蒙特卡洛模拟法进行分析,模拟次数设为 1 000次。计算结果取均值。根据生成的节点功率需求曲线利用连续潮流法求取 PV曲线,从而得到电压稳定裕度。每15min计算一次。
针对相同渗透率下的常规负荷、无序电动汽车负荷及有序电动汽车负荷,计算配网电压稳定裕度,分析电动汽车对电压稳定裕度的影响。另外,考虑电动汽车作为可控负荷参与电压稳定紧急控制的情况。
3.1 常规负荷及无序充电EV负荷对电压稳定裕度的影响对比
为了研究电动汽车负荷与常规负荷的不同之处,分别计算无序电动汽车负荷与常规负荷以相同渗透率接入配网后的配网电压稳定裕度。对每一时刻,按照上述计算方法求取电动汽车充电负荷总功率,并计算每一时刻电网电压稳定裕度。对常规负荷,每一时刻以与电动汽车相同总功率、配网各节点基础负荷比例分配到各节点,并计算电压稳定裕度。
当采用 2.2节中说明的负荷增长方式时,对系统各节点求取 PV曲线,得到各节点电压稳定裕度相同,即λmax相同。这是因为各节点负荷同比例增长,当某一节点到达电压崩溃点时,实际情况是整个配网场景的崩溃,因此任一节点的电压稳定裕度,都可作为系统电压稳定裕度值。
图 3、图 4分别给出了无电动汽车接入、相同渗透率常规负荷及无序充电电动汽车负荷接入下的各时刻系统总负荷以及电压稳定裕度。系统基础负荷功率因数为0.95。此时渗透率为20%,电动汽车接入充电站规划节点比例α=90%。从图中可以看出,电动汽车峰荷在19:00~21:00时段,与系统原负荷峰荷基本重合。相对基础负荷情况,系统负荷增加会导致电压稳定裕度降低。对各时刻而言,配网负荷与电压稳定裕度大致呈反比,负荷越重,电压稳定裕度越低。而在无序 EV充电负荷的情况下,电压稳定裕度明显低于常规负荷接入配网。这是因为电动汽车负荷大部分集中在三个充电站节点,导致上述节点的负荷明显高于常规负荷情况,当负荷增长方式为所有节点同比例增长时,即使其他节点负荷较轻,系统电压稳定裕度也受重负荷节点的约束,较快达到崩溃点。
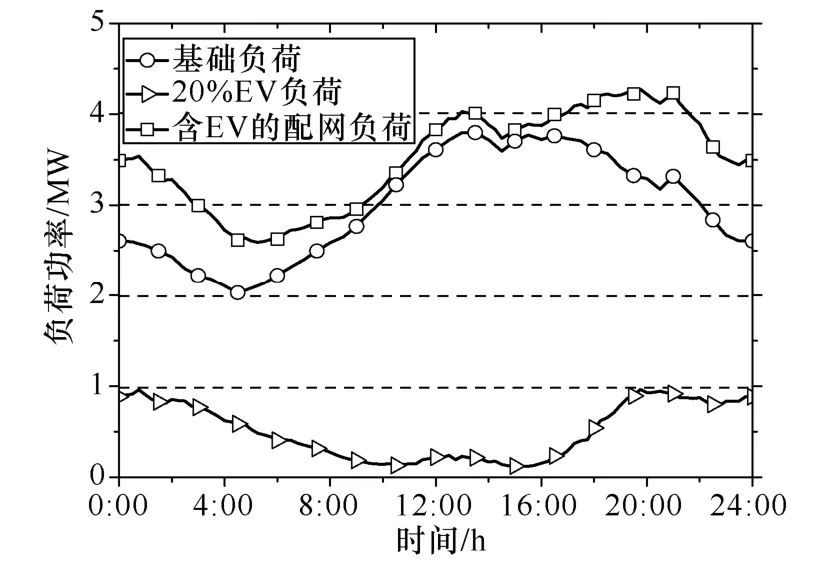
图3 20%电动汽车负荷对原负荷曲线的影响Fig.3 The impact of EVs on the load curve with 20%penetration
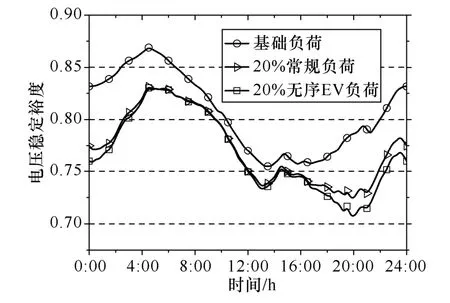
图4 20%电动汽车负荷及常规负荷对系统电压稳定裕度的影响Fig.4 The impact of EVs and regular load on the system voltage stability margin with 20% penetration
图 5给出了渗透率分别为 20%、40%、60%时的无序电动汽车负荷与常规负荷接入电网后的各时刻配网电压稳定裕度。可以看出,渗透率增大时,常规负荷对电压稳定裕度的影响变化较小,而由于电动汽车负荷集中在充电站节点,当渗透率增大时,充电站节点负荷也大量增加,从而使电动汽车对电压稳定裕度的影响随渗透率增大而急剧增大。
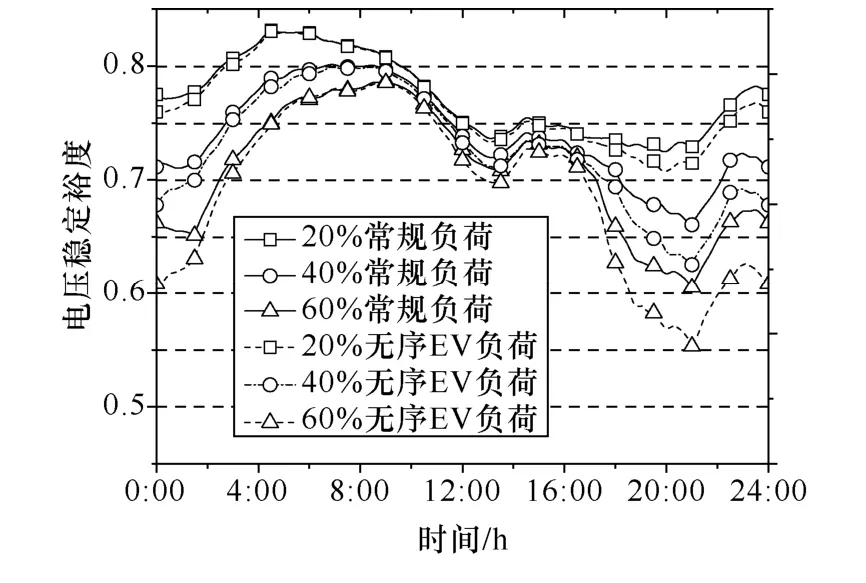
图5 不同渗透率电动汽车及常规负荷对系统电压稳定裕度的影响Fig.5 The impact of EVs and regular load on the system voltage stability margin with different penetrations
3.2 无序充电及有序充电EV负荷对电压稳定裕度的影响对比
为验证有序充电的控制效果,分别计算相同渗透率下每一时刻电动汽车在无序充电及有序充电策略下接入配网后的配网电压稳定裕度。有序充电策略采用峰谷分时充电电价策略。
图6给出了不同渗透率下无序充电电动汽车负荷与有序充电电动汽车负荷接入时的各时刻电压稳定裕度,选取α=90%。从图中可以看出,相比无序充电情况,有序充电情况有效提升了负荷高峰期时的电压稳定裕度,并充分利用了低谷时期。渗透率越高,两种情况下电压稳定裕度差别越明显。说明该有序充电策略有效地使电动汽车峰荷避开了系统峰荷,改善了系统电压稳定性。

图6 电动汽车有序与无序充电仿真结果Fig.6 Simulation results of coordinated and uncoordinated charging modes
3.3 α对配网电压稳定裕度的影响
为研究α对配网电压稳定裕度的影响,分别求取不同α下无序电动汽车负荷接入配网后的各时刻配网电压稳定裕度。渗透率设为60%。
图7给出了各时刻系统电压稳定裕度随α的变化规律。可以看出,在电动汽车负荷较轻的时刻,α对系统电压稳定裕度几乎无影响,而电动汽车大量接入时,系统电压稳定裕度随α的增大而显著减小,表明大规模电动汽车接入配电网时,电动汽车负荷越集中,对系统电压稳定裕度的约束越大。进一步说明了即使其他节点负荷较轻,系统电压稳定裕度也受重负荷节点的限制,较快达到崩溃点。
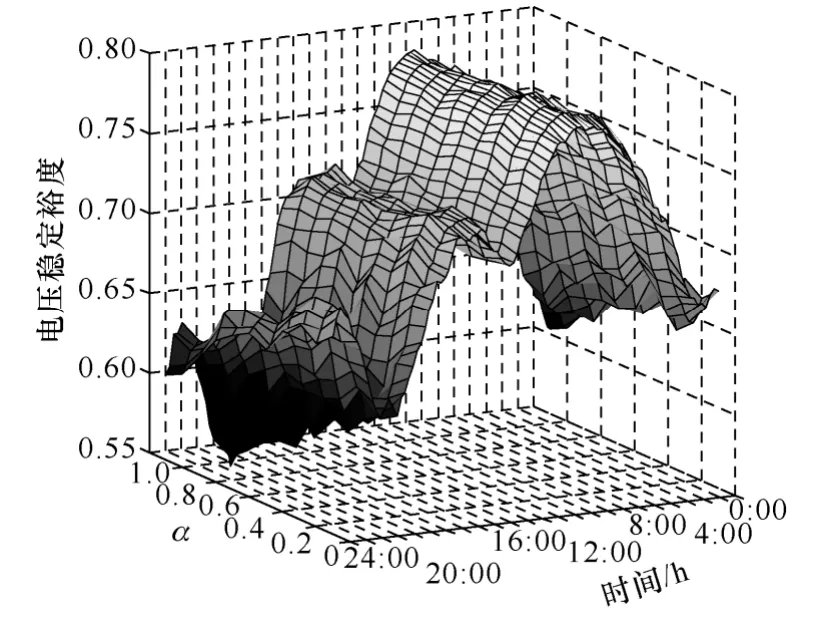
图7 α对系统电压稳定裕度的影响Fig.7 The impact of α on system voltage stability margin
4 考虑电动汽车的电压稳定紧急控制策略

图8 无序充电下电压稳定紧急控制策略结果Fig.8 Results of voltage stability emergency control under uncoordinated charging mode
图8给出了电动汽车渗透率为60%时的系统各时刻电压稳定裕度。在 19:00时已经出现了小于0.57的情况,根据上述方法采取紧急控制策略,其仿真结果如图8所示。可以看出,系统电压稳定裕度得到了有效保证。
5 结论
随着电动汽车保有量的增加,其作为用电负荷对配电网的影响将日益增大。本文在考虑影响电动汽车充电的两个关键随机因素的基础上,提出了电动汽车充电负荷概率模型。考虑将电动汽车视为可控负荷,以减少其对电网的不利影响。同时,本文对常规负荷、无序充电电动汽车负荷及有序充电电动汽车负荷对配网电压稳定裕度的影响进行了对比。结果表明,三种接入负荷中,无序充电负荷对电网电压稳定裕度影响最大,而通过对电动汽车充电行为进行引导,能显著改善电动汽车对电网电压稳定裕度带来的影响。对α的研究表明,电动汽车负荷越集中,对配网电压稳定裕度的影响越明显。另外,本文还考虑了将电动汽车作为可切负荷参与系统电压稳定紧急控制,结果表明当大量电动汽车接入电网时,参与系统电压稳定控制效果显著。
[1] 周雪松, 徐晓宁, 马幼捷. 配电系统电压稳定性概念的分析[J]. 天津理工大学学报, 2006, 22(2): 27-30.Zhou Xuesong, Xu Xiaoning, Ma Youjie. Consideration about the concept of distribution system voltage stability[J]. Journal of Tianjin University of Technology,2006, 22(2): 27-30.
[2] 伍利, 姚李孝, 古婷婷. 基于线性负荷指数不同负荷模型的辐射型配电网电压稳定性分析[J]. 电力系统保护与控制, 2011, 39(13): 8-13.Wu li, Yao Lixiao, Gu Tingting. Radial distribution system voltage stability analysis by different load models based on linear load index[J]. Power System Protection and Control, 2011, 39(13): 8-13.
[3] 陈德树, 段献忠, 何仰赞. 电力系统电压稳定性的研究现状[J]. 电网技术, 1995, 19(4): 20-24.Chen Deshu, Duan Xianzhong, He Yangzan. Review of voltage stability in electric power system[J]. Power Systern Technology, 1995, 19(4): 20-24.
[4] 王庆红, 周双喜, 胡国根. 基于扩展潮流模型的电力系统电压稳定分析[J]. 电网技术, 2002, 26(10):25-29.Wang Qinghong, Zhou Shuangxi, Hu Guogen. Power system voltage stability analysis using expanded power flow models[J]. Power Systern Technology,2002, 26(10): 25-29.
[5] 韦化, 丁晓莺. 基于现代内点理论的电压稳定临界点算法[J]. 中国电机工程学报, 2002, 22(3): 28-32.Wei Hua, Ding Xiaoying. An algorithm for determining voltage stability critical point based on interior point theory[J]. Proceedings of the CSEE, 2002, 22(3):28-32.
[6] Guimaraes M A N, Lorenzeti J F C, Castro C A.Reconfiguration of distribution systems for stability margin enhancement using tabu search[C]. IEEE International Conference on Power System Technology,2004: 1556-1561.
[7] 刘健, 毕鹏翔, 张文元. 复杂配电网的简化建模和分析[J]. 西安交通大学学报, 2002, 36(6): 564-567.Liu Jian, Bi Pengxiang, Zhang Wenyuan. Simplified modeling and analysis of complicated distribution networks[J]. Journal of Xi'an Jiaotong University,2002, 36(6): 564-567.
[8] Prada R B, Souza L J. Voltage stability and thermal limit: constraints on the maximum loading of electrical energy distribution feeders[J]. IEEE Proceedings-Generation, Transmission and Distribution, 1998,145(5): 573-577.
[9] 穆云飞. 含风电场及电动汽车的电力系统安全性评估与控制研究[D]. 天津: 天津大学, 2012.
[10] 涂轶昀, 李灿, 承林, 等. 电动汽车对电网影响的研究[J]. 广东电力, 2012, 25(5): 11-15.Tu Yiyun, Li Can, Cheng Lin, et al. Research on impact of electric automobiles on power grid[J].Guangdong Electric Power, 2012, 25(5): 11-15.
[11] 毛学魁, 王伟. 含风电配网系统电压稳定控制技术研究[J]. 华北电力大学学报(自然科学版), 2011,38(1): 39-43.Mao Xuekui, Wang Wei. Research on voltage stability control technology for distribution network including wind farm[J]. Journal of North China Electric Power University(Natural Science), 2011,38(1): 39-43.
[12] 葛晓慧, 赵波. 光伏电源接入对配电网电压稳定的影响研究[J]. 浙江电力, 2011, 30(10): 6-8, 13.Ge Xiaohui, Zhao Bo. Research on influence of photovoltaic source integration on dstribution network voltage stability[J]. Zhejiang Electric Power, 2011,30(10): 6-8, 13.
[13] 李东坡, 殷鸿雁, 张明理. 风电接入对配电网电压稳定的影响研究[J]. 东北电力技术, 2013, 34(1):29-32.Li Dongpo, Yin Hongyan, Zhang Mingli. The influences of wind power integration on the voltage stability of distribution network[J]. Northeastern China Electric Power Technology, 2013, 34(1): 29-32.
[14] 祁永福. 含分布式电源的配电网双层优化规划研究[D]. 北京: 华北电力大学, 2011.
[15] 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11):126-130.Tian Liting, Shi Shuanglong, Jia Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11):126-130.
[16] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42.Luo Zhuowei, Hu Zechun, Song Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power System, 2011,35(14): 36-42.
[17] 宫鑫, 林涛, 苏秉华. 插电式混合电动汽车充电对配电网的影响[J]. 电网技术, 2012, 36(11): 30-35.Gong Xin, Lin Tao, Su Binghua. Impact of plug-in hybrid electric vehicle charging on power distribution network[J]. Power System Technology, 2012, 36(11):30-35.
[18] 韩鹏, 汪晋宽, 韩英华. 电动汽车充电规律对配电网影响的分析与建模[J]. 东北大学学报(自然科学版), 2012, 33(12): 1702-1705.Han Peng, Wang Jinkuan, Han Yinghua. Analysis and modeling for the PEV charging regularity impact to the distribution grid[J]. Journal of Northeastern University(Natural Science), 2012, 33(12): 1702-1705.
[19] 徐立中, 杨光亚, 许昭, 等. 电动汽车充电负荷对丹麦配电系统的影响[J]. 电力系统自动化, 2011,35(14): 18-23.Xu Lizhong, Yang Guangya, Xu Zhao, et al. Impacts of electric vehicle charging on distribution networks in Denmark[J]. Automation of Electric Power System,2011, 35(14): 18-23.
[20] Kromer M A. Electric powertrains : opportunities and challenges in the US light-duty vehicle fleet[D].Massachusetts Institute of Technology, 2007.
[21] Axsen J, Burke A, Kurani K S. Batteries for plug-in hybrid electric vehicles(PHEVs): goals and the state of technology circa 2008[R]. 2008.
[22] 葛少云, 黄镠, 刘洪. 电动汽车有序充电的峰谷电价时段优化[J]. 电力系统保护与控制, 2012, 40(10):1-5.Ge Shaoyun, Huang Miu, Liu Hong. Optimization of peak-valley TOU power price time-period in ordered charging mode of electric vehicle[J]. Power System Protection and Control, 2012, 40(10): 1-5.
[23] Wynne J. Impact of plug-hybrid electric vehicles on California’s electricity grid[D]. North Carolina: Duke University, 2009.
[24] 祝达康, 程浩忠. 求取电力系统 PV曲线的改进连续潮流法[J]. 电网技术, 1999, 23(4): 39-42, 50.Zhu Dakang, Cheng Haozhong. An improved continuation method in tracing PV curves of power systems[J].Power System Technology, 1999, 23(4): 39-42, 50.
[25] Hafez O, Bhattacharya K. Optimal PHEV charging in coordination with distributed generation operation in distribution systems[C]. IEEE Power and Energy Society General Meeting, 2012: 1-7.

