400Hz有源滤波器闭环控制建模及其动态性能分析
陈 仲 陈 淼 王志辉
(南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016)
1 引言
航空供电系统担负着为飞机的雷达、导航、飞控、环控等关键系统提供高质量电能的任务,对飞机的安全、稳定运行起着重要的作用。随着飞机多电化进程的加快,机载电气设备也越来越多[1,2],在提升飞机性能的同时,其所引起的谐波污染问题也日益突出。
有源电力滤波器(ActivePowerFilter,APF)能够动态补偿谐波和无功,是一种先进的电力系统电能质量治理方案[3-5],采用有源滤波器来解决飞机电网的电能质量问题具有广泛的前景[6-12]。经典的并联型APF控制策略中,谐波检测算法是其核心,因而在航空有源滤波器中,谐波检测算法得到的关注也是最多的:如基于离散Fourier的谐波检测算法[6]、完美谐波消去法[7]、自适应选择性谐波算法[8]。当然,对电流控制器的研究也较多,如预测电流控制[9]、迭代学习控制[10]。另外,文献[11]尝试将单周控制用于航空有源滤波器中;文献[12]则首次将有源滤波技术运用至航空直流电源系统。
上述航空有源滤波器研究中,除了文献[10]和文献[11],其他都属于经典的APF控制策略,其对于APF最终的控制目标——电网电流而言,是开环控制。这就要求检测和控制中的误差必须非常小,否则将影响电网电流补偿后的精度[13]。对于基波频率为数倍于工频电网的航空电源系统而言,这些误差对航空APF补偿精度的影响尤甚。闭环控制具有抑制任何内、外扰动对被控量产生影响的能力,具有较高的控制精度[14]。因此,对电网电流进行闭环控制是提高航空有源滤波器补偿精度的一个重要措施。
本文针对中频航空应用背景,以一种闭环控制——电网电流直接控制[15]为基础,建立其系统模型,分析其用于航空电网时的局限性,并且有针对性地对其进行控制优化,以满足400Hz航空有源滤波器的静态和动态性能要求,最后通过仿真和实验来验证理论分析的正确性。
2 APF电网电流闭环控制建模
2.1 电网电流直接控制
以单相系统为例,图1给出了基于电网电流直接控制的APF控制框图。APF直流侧电压Vdc经过检测后,与基准电压V*dc比较,其差值送入电压调节器,得到电网电流基准幅值Im*;同时,通过检测电网电压vS,得到电网电流的频率和相位信息eS;利用乘法器,得到一正弦波作为电网电流基准iS*送到电流控制器,控制电网电流iS。由于需要将电网电流反馈到控制环路中,因此电网电流直接控制是一种反馈控制。
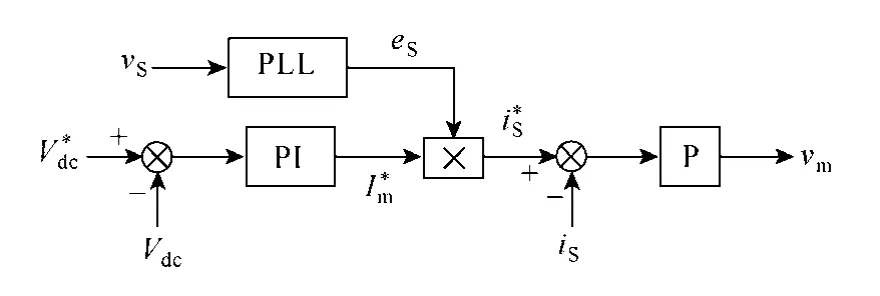
图1 电网电流直接控制框图Fig.1 Diagram of source current direct control
图1中,电网电流直接控制实现简单,能获得较好的补偿效果。但在变负载工况下,直流侧电压波动较大,系统动态响应较慢。本节通过对电网电流直接控制APF的电流环与直流侧电压环分别进行分析与建模,为下文寻找导致该控制策略动态性能较差的原因奠定基础。
2.2 电流环模型
图2给出了电网电流直接控制下APF电流环模型。这里,电流调节器采用P调节器,比例参数为K。对于PWM调制环节及电压源型逆变器,存在下列关系

式中,vC(t)为变换器输出电压;vm(t)为调制波信号;Vtri为三角载波幅值。

图2 电流环模型Fig.2 Model of current loop

式中,时间常数T=LVtri/(KVdc)。
Gir(s)反映了并联型APF的电流跟踪效果。由式(2)可知,其本质为具有一阶传递函数的电流放大器,系统转折频率为1/T。

图3 电流环传递函数伯德图Fig.3 Bode diagram of the current loop transfer function
图3给出了某组电流环参数下传递函数Gir(s)的伯德图。图3中的直流侧电压Vdc范围为200~1000V,电感值L为400~2000μH;电流环参数为:调节器比例系数K=20,三角载波幅值为10V。可以看出,在中低频段,Gir(s)的增益几乎为1,即0dB,实际的电网电流能够很好地跟踪上电网电流基准变化。随着频率的升高,电流环跟踪性能逐渐降低。另一方面,Vdc越高,L越小,电流环对高频分量的跟踪性能越好。
当然,在设计APF主电路时,L和Vdc的选取还需综合电流纹波等其他指标折衷考虑。但从图3中可知,通过对Vdc和L的优化设计,电流环不会成为影响APF动态性能的瓶颈所在。
2.3 电压环模型
下面对电网电流直接控制下APF直流侧电压环进行建模。
对于电网电流直接控制,电网电流基准的相位信息来自于检测电网电压得到的同步正弦信号,而幅值来自于APF直流侧电压调节器的输出。由于APF直流侧电压直接反映了整个系统的功率平衡变化状态,因此闭环控制的模型可以通过对系统功率的平衡方程进行推导得到。
若电网电流为与电网电压同步的正弦波,则存在如下功率平衡关系

式中,VS、IS分别为电网电压、电流的幅值;PL为负载消耗的有功功率;PC为APF提供的有功功率,稳态时,忽略APF损耗,则PC为零。
当负载功率发生变化时,式(3)可改写为

式(3)减去式(4),可以得到APF提供的功率变化量ΔPC(t)

由于APF提供的功率变化量ΔPC(t)直接反映在APF直流侧电压的变化上,则有
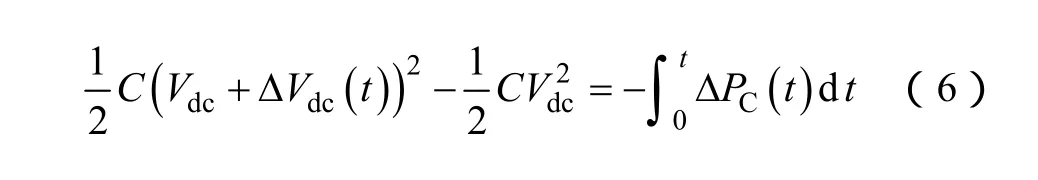
对上式做Laplace变换,考虑到ΔVdc(t)远小于Vdc,故忽略其平方项,可得

由此,即可得到基于电网电流直接控制下的并联型APF的功率模型,如图4a所示。图4a中,Kf为直流电压采样系数;Gv(s)为电压调节器传递函数,即Gv(s)=Kp+Ki/s,Kp为电压调节器比例系数,Ki为电压调节器积分系数。考虑到电流跟踪模块的响应速度远远快于直流电压环的响应速度,这里将电流环等效为一个单位线性环节,如此即可得到最终简化后的系统功率模型,如图4b所示。

图4 直流侧电压环模型Fig.4 Model of the DC-link voltage loop
从图4中可以看出,负载功率PL对整个系统的功率平衡而言是一个扰动量,对APF直流侧电压的稳定起到了干扰。
3 400Hz电网电流闭环控制的局限性
3.1 负载扰动对电流基准的影响
由图4b可知,在实功率模型中,负载功率PL作为扰动量作用于APF系统,扰动量PL(s)到ΔVdc(s)的传递函数为

由于电网电流基准是通过电压调节器对直流侧电压误差进行PI调节后得到,因此,电网电流基准IS*(s)与负载电流IL(s)之间的传递函数HiL(s)可以如下表示
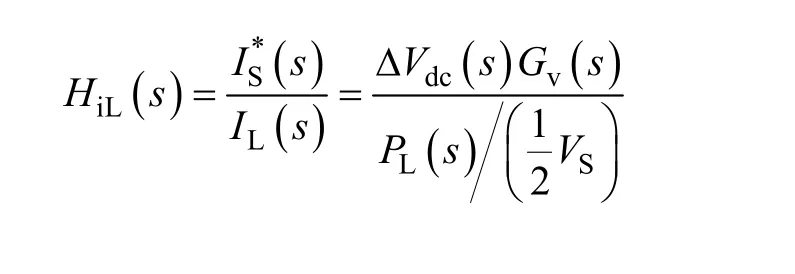
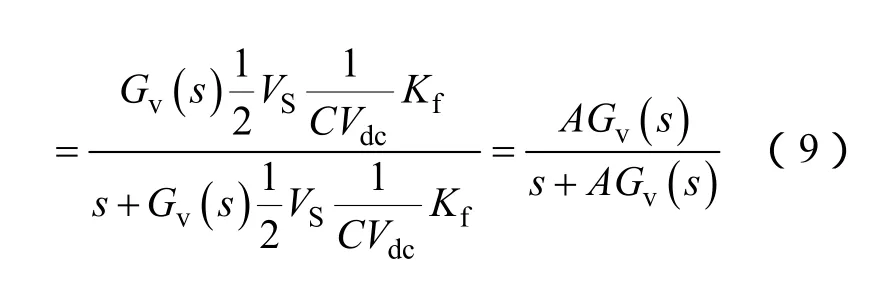
式中,A=VSKf/(2CVdc),其与电网电压、直流侧电容电压、直流侧电容值以及电压采样系数有关。
3.2 电网电流控制用于400Hz电网的局限性
HiL(s)反映了电网电流直接控制策略中,电网电流基准iS*跟随负载电流iL变化的响应速度。又由于电网电流跟踪其基准速度远远快于直流电压环的响应速度,因此,HiL(s)近似反映了系统实际的电网电流iS跟随负载变化的动态性能,是衡量系统动态性能的一个重要指标。
从式(9)可知,系数A的值以及电压调节器参数是影响系统动态性能的两个关键因素。图5给出了A变化时,传递函数HiL(s)的幅频特性曲线对比图,此时电压调节器Gv(s)=1+1/s。从图5中可知,随着A值的增大,HiL(s)的增益也在不断增大,但是对于航空电网而言,其在400Hz基频处的增益仍然较小,这就意味着有源滤波器系统的动态性能较低。要获得较高的动态性能,HiL(s)就必须有足够大的增益,则A值必然取很大,即C或Vdc的取值很小,但在实际系统中,由于需要满足APF直流侧电压纹波以及电流纹波的相关要求,C值和Vdc值的选择裕度较窄。因此,通过增大A值来提高HiL(s)的增益是不现实的。本节中APF的系统参数如下:电网电压115V/400Hz,直流侧电容680μF,直流侧电压300V,电压采样系数0.01,经过计算后,A值为4。

图5 A值对HiL(s)的影响Fig.5 Influence of A on the magenitude of HiL(s)
另一种增大HiL(s)增益的方法为改善电压调节器的调节速度。图6给出了A值为4时,三种电压调节器参数下HiL(s)的幅频特性曲线对比。可见通过对电压调节器参数的优化,HiL(s)的增益明显提高。对于50Hz工频电网来说,通过优化电压调节器参数可以勉强将HiL(s)的带宽提升到较为合适的程度,满足APF的动态性能要求。但是,对于航空电网而言,其基波频率为400Hz,从图6中可以看出在相同的电压调节器参数下,400Hz处HiL(s)的增益比50Hz时小18dB。因此,在保证系统稳定的前提下,无论电压调节器参数如何优化,HiL(s)针对航空电网时的增益都非常低,APF的动态响应很慢。

图6 PI参数对HiL(s)的影响Fig.6 Influence of PI on the magenitude of HiL(s)
对于采用电网电流直接控制的并联型APF,由于其电网电流基准幅值由直流侧电压误差经过电压调节器放大后产生,负载突变时,电网电流基准通过较慢的电压调节器进行缓慢的调节,导致APF的电网电流基准难以在短时间内跟踪上负载电流的变化,而正是这一点导致了电网电流直接控制并联型APF较差的动态响应。尤其对于航空应用场合,系统的动态响应将更加难以满足实际系统动态性能指标的要求。因此,在航空APF中,应用电网电流直接控制具有其局限性。
4 负载基波有功电流前馈特性分析
根据经典控制理论中对于系统扰动补偿的思想,本节通过应用针对扰动的前馈补偿策略,可以显著地提高系统的动态响应速度。
4.1 复合控制思想的引入
经典控制理论指出,如果控制系统中存在强扰动,特别是低频强扰动,或者系统的稳态精度和响应速度要求很高,则一般的反馈控制难以满足要求。复合控制是在系统的反馈控制回路中加入前馈通路,组成一个前馈控制与反馈控制相结合的系统,只要系统参数选择合适,不但可以保持系统稳定,极大地减小乃至消除稳态误差,而且可以抑制几乎所有的可测量扰动,包括低频强扰动[14]。
图7所示为按负载扰动补偿的复合控制模型。通过恰当设计前馈补偿装置的传递函数Gn(s),使扰动量PL(s)对系统输出产生补偿作用,以抵消扰动PL(s)对输出的影响。

图7 按负载扰动补偿的复合控制模型Fig.7 Model of load disturbance compensation
根据自动控制理论,为消除扰动作用下的误差,通常采用对扰动的误差全补偿,则其前馈补偿装置的传递函数如下

前馈控制可以有效地减轻反馈控制的负担,在这里,反映为反馈控制量在电网电流基准IS*(s)中所占的比重降低,因此系统的动态性能受直流侧电压环影响的程度降低。
4.2 负载基波有功电流前馈
全补偿可实现负载功率对直流侧电压Vdc(s)扰动的全补偿。但此时负载有功电流中的谐波分量也前馈至电流基准IS*(s),这是不希望的。
对于负载功率,其中的主体成分是以负载电流的基波成分产生的,该分量对于直流侧电压的影响最大;同时,电网电压正弦时,负载电流中的谐波成分是无法产生有功功率的。因此,本文提出将负载基波有功电流进行前馈补偿,电网电流的基准信号由电压环反馈输出与负载基波电流前馈输出共同组成,这样就得到了基于负载基波有功电流前馈的APF复合控制,其控制模型如图8所示。图中,Iff(s)为前馈控制分量,Ifb(s)为反馈控制分量。

图8 负载基波有功电流前馈补偿Fig.8 Load active current feedforward compensation

其中,对于负载基波前馈环路中的传递函数为F(s),在这里选择低通滤波器(Low Pass Filter,LPF),用以提取负载功率中的直流分量进而计算出负载基波有功电流,其阶数n为1、2、3时的传递函数分别为
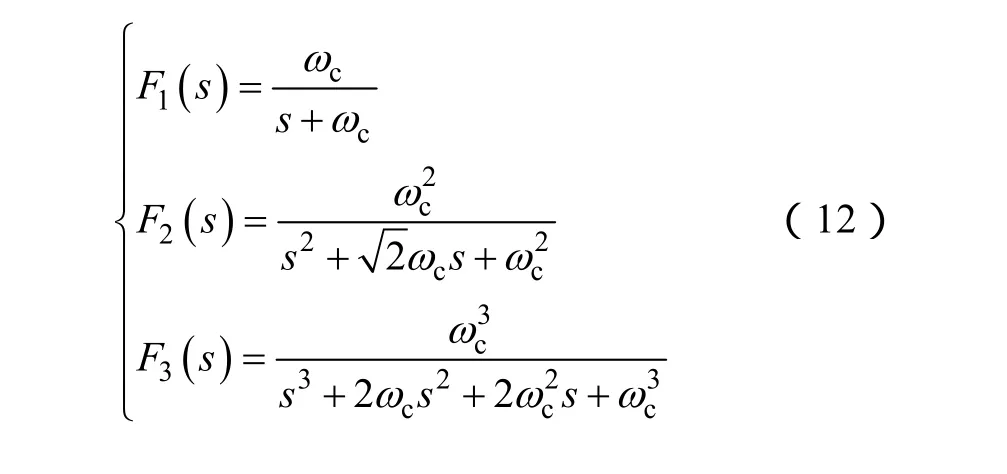
式中,ωc为LPF截止角频率,则其截止频率fc=ωc/2π。
为了考察引入前馈补偿对APF性能的改善,图9给出了反馈控制以及引入负载基波有功电流前馈的复合控制下,电流基准对于负载变化的幅频特性曲线。这里的电压调节器传递函数Gv(s)=10+100/s。图中复合控制前馈通道中LPF的截止频率fc分别80Hz和 400Hz。


图9 不同LPF阶数下HiL(s)增益Fig.9 Magenitude of HiL(s) under different LPF orders
如图9所示,在仅使用反馈控制时,系统带宽较窄,50Hz之后的信号增益很低。引入前馈补偿后,系统的带宽明显变宽,说明系统的动态性能得到了提高。同时,前馈通道中LPF的转折频率越高,系统的带宽越宽,动态性能越好,但是对高于400Hz的信号扰动抑制能力会降低,在实际中会具体表现为电网电流存在畸变。当LPF的阶数增加时,系统对400Hz之后的中高频信号的衰减能力变强,电网电流精度更好,然而其对转折频率到400Hz附近的信号衰减也更大,并且此时幅频特性曲线以近似-60dB/格衰减,系统相位延迟也更加严重,因而系统的动态性能和稳定性有所降低。综上所述,LPF参数的选取对前馈补偿的性能改善起到了十分重要的作用。
5 仿真与实验验证
为了验证理论分析的正确性,本节分别对基于反馈控制和基于负载基波有功电流前馈的复合控制的APF进行了仿真和实验验证。验证中,APF的补偿容量设计为3kV·A,负载为典型的三相二极管整流桥带阻感负载。具体的系统参数见下表。

表 3kV·AAPF 系统参数Tab. Parameters of 3kV·A prototype
5.1 工频电网频率下的仿真结果
图10为220V/50Hz工频系统下的APF动态响应仿真结果。负载在0.5s的时候切除,在0.6s的时候投入。三个仿真波形分别为u相负载电流、补偿电流和电网电流。从图10中可以看出,APF的动态响应较快,基本可以在两个电网周期内完成动态变化过程。这也验证了前文所得到的结论:传统电网电流直接控制的APF应用在50Hz工频电网中,通过对电压环的优化设计,可以使其动态性能达到一个较为理想的水平。

图10 50Hz工频电网下反馈控制仿真Fig.10 Simulation of feedback control under 50Hz grid
5.2 400Hz电网下的系统验证
首先对前馈补偿用低通滤波器的截止频率fc对系统性能的影响进行仿真,图11分别给出了三种不同截止频率下u相电网电流基准幅值的仿真波形。从图中可以看出,当截止频率较小时,系统的动态响应过程较慢,调节时间较长,但是电网电流基准幅值的纹波较小,即系统静态性能较佳;随着截止频率的增大,动态响应速度得到提升,但此时电网电流基准幅值的纹波也随之变大,系统的静态性能受到影响。

图11 LPF截止频率对系统性能的影响Fig.11 Influence of fcon system performance

图12 LPF阶数对系统性能的影响Fig.12 Influence of LPF order n on system performance
图12给出了滤波器阶数n分别取1、2、3时的仿真波形。可以看到,滤波器阶数越高,电网电流基准幅值的精度越好,但是动态响应速度会变慢,滤波器所需的元器件也会增加;当低通滤波器阶数为1阶时,电网电流基准幅值的变化速度很快,而且调节时间亦较短,但是此时其纹波达到了10A左右,静态性能较差。因此滤波器的阶数也需综合系统对动、静态性能以及滤波器实现成本综合考虑,一般2阶的低通滤波器就已能满足要求。
经过仿真对比,最终选取2阶,截止频率设为160Hz的低通滤波器来进行400Hz系统的实验验证。
图13为只采用反馈控制的APF动态波形,从结果中看出,当负载突变时,电网电流变化很慢,不能快速响应负载的变化,并且从卸载时补偿电流波形看出,在动态过程中APF主电路存在过电流现象,并且持续时间较长,这就有可能导致系统保护误触发,或者损坏开关管。
图14给出了复合控制下系统的动态波形,可见引入前馈补偿之后,系统的动态响应速度有很大幅度的提升,并且过电流现象基本不存在,与只采用反馈控制的系统相比,APF动态性能有大幅度的提升。

图13 反馈控制下系统动态波形Fig.13 Waveforms of dynamic performance underfeedback control

图14 复合控制下系统动态波形Fig.14 Waveforms of dynamic performance undercomposite control
6 结论
(1)本文通过基于电网电流闭环控制的并联型APF控制系统进行建模和分析,指出:对于普通50Hz工频电网,通过控制参数的优化,基于电网电流直接控制的APF可以满足其动态性能要求;但是对于航空400Hz电网而言,其动态性能较差,应用具有局限性。
(2)在揭示400Hz有源滤波器动态性能内在机理的基础上,引入负载基波有功电流前馈补偿,组成复合控制系统以改善电网电流闭环控制APF应用于航空电网时的动态性能,从幅频特性曲线的分析和对比中可知,复合控制大大提高了APF系统的动态性能。
(3)建立了复合控制APF系统的实验平台进行验证,结果表明,经过参数优化设计后,这种采用复合控制的航空有源滤波器具有良好的动态性能,可以快速有效地补偿由于负载的非线性产生的谐波和无功分量。
[1] Moir I, Seabridge飞机系统:机械、电气和航空电子分系统综合[M].3版.凌和生,译.北京:航空工业出版社,2011.
[2] Rosero J A, Ortega J A, Aldabas E, et al. Movingtowards a more electric aircraft[J]. IEEE Aerospaceand Electronic Systems Magazine, 2007, 22(3): 3-9.
[3] Akagi H, Watanabe E H, Aredes M. Instantaneouspower theory and applications to power conditioning[M]. Piscataway, NJ: IEEE Press, 2007: 109-110.
[4] Singh B, Al-Haddad K, Chandra A. A review ofactive filters for power quality improvement[J]. IEEETransactions on Industrial Electronics, 1999, 46(5):960-971.
[5] 陈国柱,吕征宇,钱照明.有源电力滤波器的一般原理及应用[J].中国电机工程学报,2000,20(9):17-21.Chen Guozhu, Lü Zhengyu, Qian Zhaoming. Thegeneral principle of active power filter and itsapplication[J]. Proceedings of the CSEE, 2000, 20(9):17-21.
[6] Lavopa E, Summer M, Zanchetta P, et al. Real-timeestimation of fundamental frequency and harmonicsfor active power filters applications in aircraftelectrical systems[J]. IEEE Transactions on IndustrialElectronics, 2009, 56(8): 2875-2884.
[7] Eid A, Abdel-Salam M, El-Kishky H, et al. On powerquality of variable-speed constant-frequency aircraftelectric power systems[J]. IEEE Transactions onPower Delivery, 2010, 25(1): 55-56.
[8] Venturini R P, Mattavelli P, Zanchetta P, et al.Adaptive selective compensation for variable frequencyactive power filters in more electrical aircraft[J. IEEETransactions on Aerospace and Electronic Systems,2012, 48(2): 1319-1328.
[9] Odavic M, Zanchetta P, Summer M. A low switchingfrequency high bandwidth current control for activeshunt power filter in aircrafts power networks[C].IEEE Industrial Electronics Annual Conference,Taipei, 2007: 1863-1868.
[10]Liu J, Zanchetta P, Degano M, et al. Highperformance iterative learning control for activefilters in aircraft power networks[C]. 36th AnnualConference on IEEE Industrial Electronics Society.Phoenix, AZ, United States, 2011: 2055-2060.
[11]王永,沈颂华.空间矢量和单周控制三相航空有源电力滤波器[J].北京航空航天大学学报,2007,33(1):90-93.Wang Yong, Shen Songhua. Three-phase aeronauticalactive power filter based on space vector andone-cycle control[J]. Journal of Beijing University ofAeronautics and Astronautics, 2007, 33(1): 90-93.
[12]Chen Z, Chen M, Luo Y, et al. Low frequency ripplecurrent compensation with DC active filter for thesingle-phase aeronautic static inverter[C]. 3rd IEEEEnergy Conversion Congress and Exposition, Phoenix,AZ, USA, 2011: 1468-1475.
[13]Green T C, Marks J H. Control techniques for activepower filters[J]. IEE Proceedings of Electric PowerApplications, 2005, 152(2): 369-381.
[14]胡寿松.自动控制原理[M].5版.北京:科学出版社,2007.
[15]Wu J C, Jou H L. Simplified control method for thesingle-phase active power filter[J]. IEE Proceedingsof Electric Power Applications, 1996, 143(3): 219-224.

