稠油集输伴热管道轴向温度场数值模拟算法研究

陈春，徐太贵，杜培楠，李博，刘汉强，姜帅, 陈飞，宝月

（1. 中国石油大学（北京），北京 102249； 2. 中国石油集团东南亚管道有限公司，北京 100083；3. 中原油田分公司油气储运管理处，河南 濮阳 457165; 4. 常州大学，江苏 常州 213016）

我国稠油资源分布广泛，预计资源量达300´ 108t。随着陆上大多数主力油田进入“双高”（高采出程度、高含水率）和产量递减阶段，加大对稠油资源的开采力度，必将成为我国能源领域的发展趋势[1]。在稠油集输的过程中，常采用热水外伴热的方式对其进行加热，以降低粘度，保证其流动性能。由于稠油具有密度大，粘度高，流动性差的特点，每年集输系统中动力和热力消耗巨大[2]。同时，在对稠油伴热系统进行设计时，使用的热力和水力分析方法通常偏于保守，造成了一定的浪费。本文对稠油伴热系统温度场数值模拟提出了新的方法，为稠油伴热系统水力热力耦合求解奠定基础。

1 物理问题描述

将热水管道、稠油管道以及管道与保温层间的空气分别看做温度均匀介质，求解能量方程可以得到稠油伴热系统的温度场初步分布结果，但是此结果不够精确。在此初步计算的结果之上确定某一管段的热水温度，可以将热水温度与伴热系统外界空气温度作为边界条件，求解稠油温度。求解过程的难点在于：①管段内热水温度固定后，可将热水看做非流动状态，然而稠油处于流动状态，不能将稠油的导热看做简单的稳态问题；②钢管与空气及保温层处于静态，其导热为稳态过程，欲得到稠油温度场，两者需要耦合求解。

2 数学模型建立

为求解此物理问题，需将其做必要简化：①忽略系统内稠油管道、热水管道与防腐层间的空气自然对流换热，看做简单的热传导；②忽略两种介质之间的接触热阻。表1为符号说明。

表1 符号说明Table 1 Explanation of symbols

由于计算区域的不规则性，在极坐标下求解此物理问题。下面给出稠油伴热系统径向导热过程的数学模型。能量方程如下式：

3 网络划分

结构化极坐标网格的实施主要涉及参数 与参数 的计算，由于计算区域关于x轴对称，故划分网格时，只需划分x轴上方区域，将区域分为三部分：BOF，AOB，EOA，如图1所示，其中，A、B、C、D为切点。

图1 网格划分参数函数关系示意图Fig.1 The schematic of mesh parameter function

通过角度的大小来识别三个区域，通过数学推导，可得：

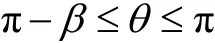
对应三个区域的极距的计算函数，例如，OG、OH、OI，计算函数为：

按精度需求将极轴旋转一周 2π角度分成 Nq份，将极距分成Nr份，参考文献[3]做法，并将保温层区域、管壁区域加密，进行计算区域的网格划分。通过函数控制将网格分为保温层、空气、管道、热水以及稠油五个部分。

为了实施有限容积法，需求得各个节点的控制容积，由于计算区域不规则，控制容积的计算比圆形计算区域极坐标网格、直角坐标系均分或非均分网格复杂得多，针对三个不同的网格划分区域，分别推导控制容积的计算公式，得到不同节点的控制容积，并可知远离极点处节点的控制容积大，网格加密处节点控制容积小，符合网格特点。使用函数控制将保温层、空气、管道、热水以及稠油五部分抽离出来，区域面积的相对偏差为0.013%，符合精度要求。

4 方程离散

对保温层、空气、管道、热水以及稠油的导热方程(1)在极坐标控制容积上进行离散,为保证物理问题的物理意义，需将物理平面映射到计算平面中去，来实施有限容积法[4]。

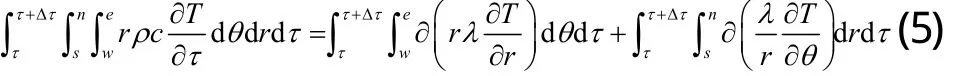
将上式整理成通用的离散化方程形式：

式中各符号含义和关系如图2所示。

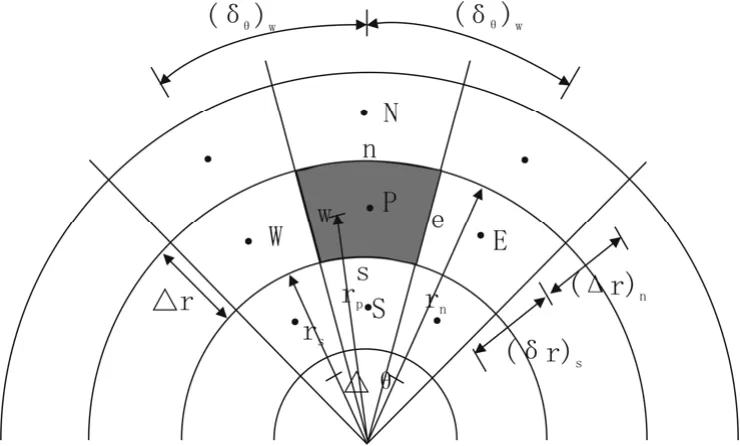
图2 离散参数示意图Fig.2 The schematic of discrete parameters

5 方程求解

图3 问题简化模型Fig.3 The simplified model

综上所述，稠油温度的求解转变为以下问题：以长度L的热水管段截面上的平均温度作为第一类边界条件，以及伴热系统外界空气温度作为第三类边界条件，求解稠油截面上温度分布，此问题为非稳态导热问题，非稳态过程的总发展时间为采用高斯-赛德尔求解器进行求解，求解过程中处理的两个难点及解决方案如下：

(1)难点1：极坐标奇点的处理方法

极坐标下划分网格求解物理问题，按照有无奇点可将网格分为两类。奇点形成的原因为：当极坐标的极点被包含在计算区域内时，极点周围的控制容积由矩形退化为三角形，且极点被周围的三角形控制容积所共有。

目前，对于奇点的处理有：线性差分和能量守恒等方法[5]。本研究采用符合物理意义的分块线性差分方法，奇点为水管与油管的切点处，在奇点处热量由水管传向油管，水管温度高于油管，因此将奇点一分为二，一个使用油管内的奇点周围节点线性差分，并将差分结果纳入到油管内的节点离散系数中去，另一个使用水管内的奇点周围节点线性差分，并将差分结果纳入到水管内的节点离散系数中去，这样便满足了热流方向的物理意义。

(2)难点2：边界条件的处理方法

尽管热水温度与伴热系统外界的空气温度已知，导热求解方程封闭，但是，稠油的真实边界条件为稠油管道的温度。稠油管道与系统内的空气，保温层温度未知，这是求解稠油温度分布不可避免的问题。解决此问题可以采用处理第三类边界条件的边界更新法思想，本研究将系统内空气、稠油管道以及保温层作为动态边界条件，即将三者与稠油温度同样看做为非稳态传热，非稳态传热结束之后，将计算出的温度场作为初场，而稠油温度初场仍为上一管段末的温度分布，再次进行迭代耦合求解，直到上下两次求解结果的相对偏差符合精度要求为止，此时，系统内空气、稠油管道以及保温层的温度场为真实的稳态温度场。

6 算例分析

为便于对数值计算的分析，假设热水流量足够大以至于整个伴热系统热水管线上，热水温度保持为90 ℃，稠油入口温度为50 ℃，平均流速1 m/s，水管管径0.4 m，管壁壁厚0.01 m，油管管径0.6 m，管壁壁厚0.01 m，保温层厚度0.01 m，系统外界空气温度为0 ℃。在此条件下，当投入到管道内的稠油横截面运行1 000 s后，其整个系统、稠油、保温层的温度场分布如图4-6所示。

图4 伴热系统温度场Fig.4 The temperature field of heating system

图5 稠油温度场Fig.5 The temperature field of heavy-oil

从图中可以看出，靠近热水管道处的稠油温度较高，远离热水管道一侧的稠油温度较低，靠近保温层处，存在一定的温度梯度，这符合稠油伴热系统的温度场特征；图中显示，保温层中存在非常大的温度梯度，这符合保温层导温系数低，保温性能好的特点。

图6 保温层温度场Fig.6 The temperature field of insulation

7 结 论

（1）本文建立了新的稠油伴热系统轴向温度场计算的物理模型与数学模型，对求解过程进行了详细描述；

（2）对稠油热传导过程进行的详细的分析与描述，并对数值模拟过程中极坐标奇点处理方法以及边界条件处理方法进行了研究。通过对算例计算结果进行分析，证明此算法对稠油伴热系统温度场进行很好的数值模拟。

［1］ 李雪峰. 稠油集输系统的热力学分析[D]. 大庆:大庆石油学院,2007.

［2］刘文胜,郭东旭.稠油输送技术及方法[J].石油科技论坛,2008(2):53-57.

［3］ 陶文铨. 计算传热学的近代进展[M]. 北京: 科学出版社, 2000.

［4］ 陶文铨. 数值传热学[M]. 第2版. 西安:西安交通大学出版社，2001.

［5］ Koji Fukagata. Highly energy-conservative finite difference method for the cylindrical coordinate system[J].J.Comput Phys., 2002, 181:478-498.