基于不完全齿轮齿条机构的小车转向系统研究

邹光明， 尹志朋， 王东雄， 刘源泂， 汪豪蒂

（武汉科技大学机械自动化学院，武汉430081）

0引言

针对第三届全国大学生工程训练综合能力竞赛的主题，本文就无碳小车的转向系统进行了设计。设计要求为：设计一种小车，驱动其行走及转向的机械能由给定的重力势能转换而来。给定重力势能为4J（取g=10 m/s2），竞赛时统一用质量为1 kg的重物块（φ50 mm×65 mm，普通碳钢）铅垂下降来获得，落差400±2 mm，重块落下后，须被小车承载并同小车一起运动，不允许从小车上掉落。要求小车具有转向控制机构，以绕过间距为1 000 mm的障碍物。对于小车转向系统，文献［1］采用凸轮机构实现转向，而本文采用齿轮齿条机构完成小车自动转向功能，关

于齿轮齿条机构的研究，一直为国内外学者所关注，在参考相关文献［2-5］基础之上完成了本转向系统的设计。

1 转向系统工作原理

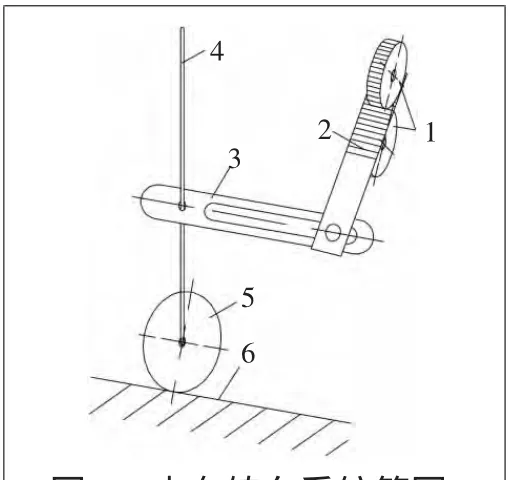
图1 小车转向系统简图

小车在运行过程中应避开间距为1 000 mm的多个障碍物，故小车需设计转向机构。转向系统简图如图l所示，齿轮传动系统带动两个不完全齿轮转动，使得不完全齿轮齿条机构中的齿条推动转向杆往复转动，以此控制前轮左右摆动，从而达到转向的目的。

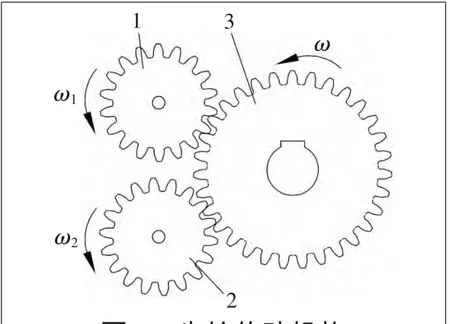
图2 齿轮传动机构

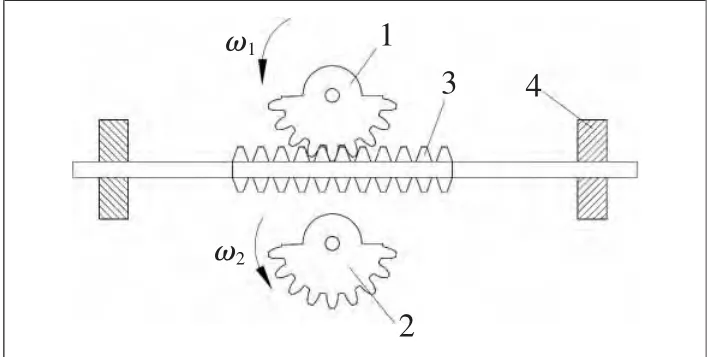
图3 用于转向的不完全齿轮齿条机构

图2中，重物下落的重力势能转化为机械能从主动轮3输入，带动两个尺寸完全相同的从动轮1和2转动。图3中不完全齿轮1和不完全齿轮2的尺寸完全相同，它们分别和图2

中的从动轮1与从动轮2同轴安装。当主动轮顺时针转动时，从动轮1和与之同轴的不完全齿轮1以及从动轮2和与之同轴的不完全齿轮2均逆时针转动。不完全齿轮1和不完全齿轮2分别与齿条啮合构成转向机构，如不完全齿轮1与齿条开始进入啮合，齿条向前运动，带动转向杆使小车向左转向，此时不完全齿轮2与齿条未啮合；当不完全齿轮1、2均逆时针转过180°时，不完全齿轮1和齿条退出啮合，不完全齿轮2和齿条进入啮合，齿条向后运动，带动转向杆使小车向右转向，此时不完全齿轮1与齿条未啮合；当不完全齿轮1、2均再逆时针转过180°时，不完全齿轮2与齿条退出啮合，不完全齿轮1与齿条进入啮合，这样便完成了不完全齿轮旋转一周齿条向前、向后各运动一次使得小车向左、向右各转弯一次的周期运动。

2 小车运动轨迹方程

根据小车转向系统分析可知，小车的运动轨迹是由几段抛物线组成，其轨迹如图4所示。图4中A为小车偏离赛道中心线最远距离，两障碍物之间的距离为1 000 mm。

设小车运动轨迹方程为y=f（x），以前1/4个周期考虑，

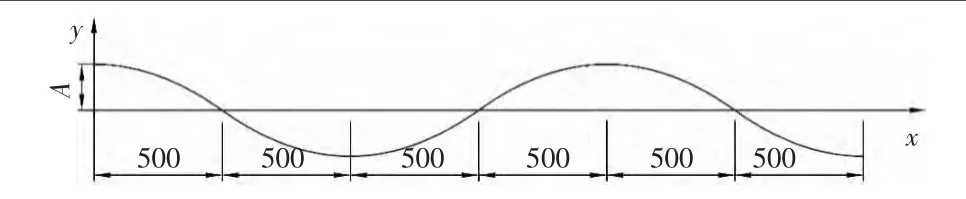
图4 小车运动轨迹

综合考虑小车的结构和运动的可靠性，A取120mm。

设过轨迹上的任一点作轨迹的切线，其斜率为tanβ；

式中：β为前轮与x正方向的夹角。

又由于前轮与x正方向的夹角就是此时转向杆的转角，如图5所示，设齿条的位移为 b，其中心线与前轮支架的距离为c，规定β在转向杆右边为正，左边为负。

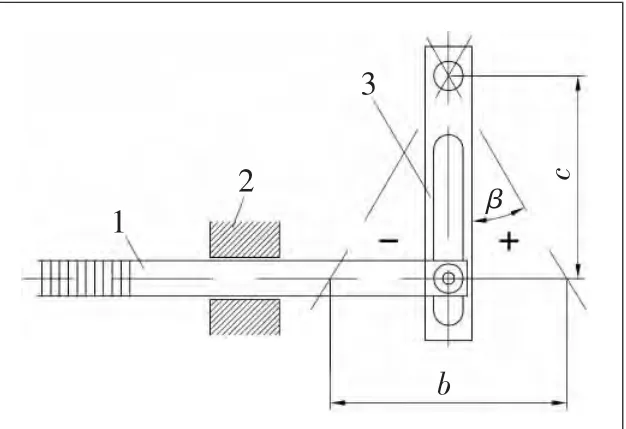
图5 转向杆与齿条的关系

当x=500mm时，前轮与水平位置有最大偏角，即导向杆处于极限位置，此时

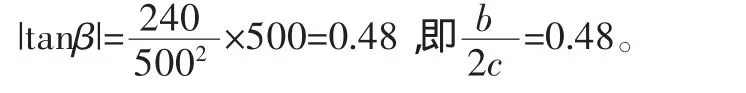
从小车整体尺寸考虑，如c值取值较大，则会使车体尺寸较大，造成小车重量太大；如c值取值较小，则小车不易转向的力较大。综合考虑后取c=30mm，b=0.48×2c=28.8mm。

3 不完全齿轮设计

3.1 首尾两齿啮合分析

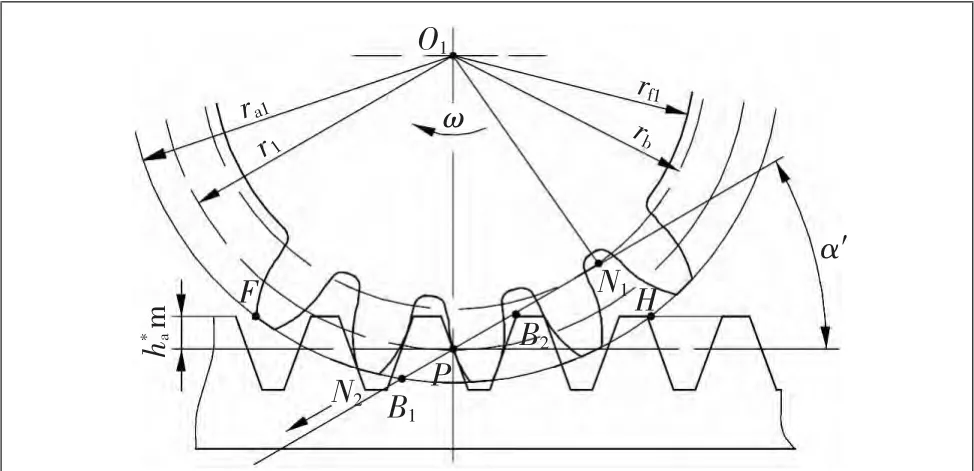
图6 不完全齿轮齿条啮合分析

要使小车达到预期的转向功能，不完全齿轮与齿条的啮合线应保证一定的长度s，使得当其中一个不完全齿轮与齿条刚好退出啮合时，另一个不完全齿轮刚好进入啮合，这样才能保证轮齿啮合运动的连续性且不产生卡死现象。在图6所示的一个不完全齿轮与齿条啮合中，当不完全齿轮的第一个齿运动到齿轮齿顶圆与齿条上齿面的交点H时，齿轮和齿条相互接触，随着不完全齿轮的转动，不完全齿轮和齿条的接触点将沿着齿条的齿顶线从H点移动到B2，相比于完全齿轮与齿条啮合，其啮合线增加了约等于B2H段的长度，不完全齿轮最后一个齿运动到B1时，由于后面没有轮齿进入啮合，所以不完全齿轮和齿条并未脱离啮合，这时不完全齿轮继续转动，此时不完全齿轮的齿顶将沿着齿条的齿廓向齿顶滑动，直到滑动到F时才脱离接触，相比于完全齿轮与齿条啮合，其啮合线增加了段的长度。其中和段不在啮合线上，传动比是变化的，小车运动轨迹会发生一定的偏差，但由于传动比变化不大，可以认为传动比近似不变；并且当不完全齿轮与齿条处于和段时，小车是运动在赛道中心线附近的，对小车避障影响较小，故小车实际运动轨迹符合避障要求。

3.2 啮合线长度的计算

假设不完全齿轮的齿数为z′，该不完全齿轮是由齿数为z的齿轮除去若干个齿得到的。由不完全齿轮首尾两齿与齿条啮合过程的分析可知，当z′＝z/2时，齿轮齿条在啮合运动的过程中会发生卡死现象，即当其中一个不完全齿轮与齿条还未退出啮合时，另一个不完全齿轮已进入啮合，这是不允许的。因此不完全齿轮在半齿数为z/2的基础上，必须再去除一定的齿数N，才能保证轮齿啮合运动的连续性且不产生卡死现象，此时得到的不完全齿轮的齿数为 z′＝z/2－N。

齿轮齿条重合度计算公式［6］如下：

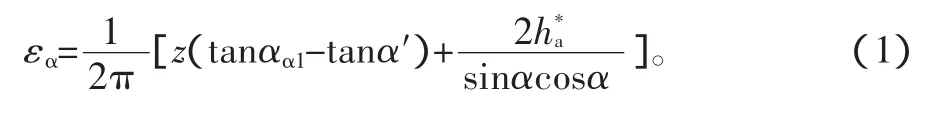
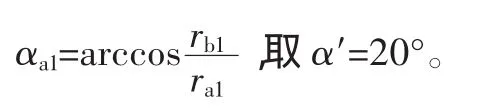
由图6分析计算可得：

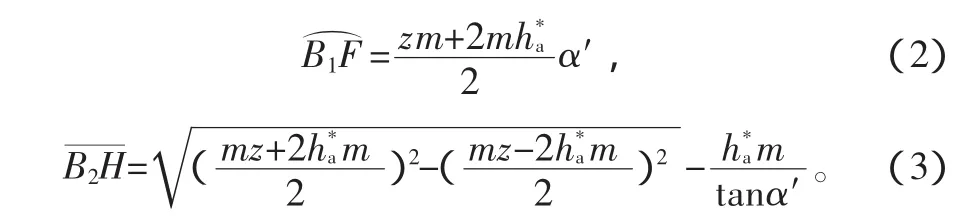
由啮合重合度的物理意义得一个不完全齿轮与齿条的总啮合线长度为：

一方面，一个不完全齿轮总长度为s的啮合线应当能够推动齿条前进的距离为f，另一个不完全齿轮总长度为s的啮合线也应当能够推动齿条后退的距离为f，而这个距离f应该等于齿条位移为b，这样才能完成一个转向周期。则有：

B1B2段齿条移动的距离为B1B2cosα′；B2H段齿条移动的距离为B2H；故当不完全齿轮有个齿时，结合重合度的意义可得：

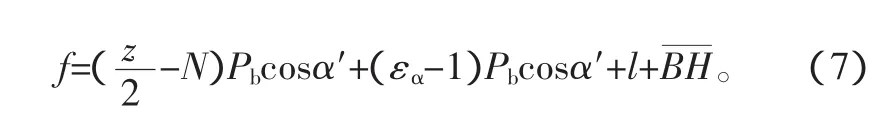
而因去除N个齿所减少的啮合线的长度应该等于由于不完全齿轮与齿条啮合时首尾两个齿对应增加的啮合线的长度，这样才能保证轮齿啮合运动的连续性且不使其卡死，则有下式：

取模数 m=0.5mm，α′=20°，将式（1），（3），（6）代入式（7），（8），联立式（5），（8）经编程计算得到，当 z=36，N=4时，f=27.89mm；NPb=6.01mm，l+B2H=6.28mm。此时将c修正为 29mm，则 b=27.84m；即此时有 f≈b，l+B2H≈N×Pb，满足式（5）、（8）的条件。

所以不完全齿轮的齿数为z′=z/2-N=14。

4 齿条尺寸的设计

齿条有齿段的最小长度Lmin应等于齿条的最大位移，即Lmin＝b=28.8mm，为满足齿条与不完全齿轮正确啮合的条件，其模数m也为0.5mm。

综上所述，不完全齿轮的模数为m＝0.5mm并且是由一个齿数为z=36的齿轮除去22 个齿得到（此时 z′=14）；齿条模数为m=0.5mm，其有齿段最小长度为Lmin=27.84mm；齿条中心线与前轮支架的距离为c=29mm。

图7即为所设计小车的整体模型。

图7 小车整体模型

5结语

本文对小车转向系统进行了详细设计，依靠半齿轮齿条机构控制小车的运行方向，使得小车按抛物曲线运动。小车在运行过程中有一定冲击存在，运动平稳，能满足小车自动转向的要求。

［1］ 杨秀光，邹光明，黄川，等.避障小车转向系统的设计［J］.机械传动，2012，36（4）：41-43.

［2］ Nicolae Oancea，Virgil Teodor，Ionut Popa.An efficient approximate profiling method for the rack gear tool［J］.Victor OanceaThe International Journal of Advanced Manufacturing Technology，2009，45（3/4）：326.

［3］ GIBSON Dan，KRAMER S.Kinematic design and analysis of the rack-and-gear mechanism for function generation［J］.Mechanism and Machine Theory，1984，19（3）：369.

［4］ 张元越.基于曲柄齿轮齿条的串联导杆机构高阶停歇的传动设计与研究［J］.机械设计，2011，28（3）：6-8.

［5］ 王猛，李长春.不完全齿轮自动转向机构的运动分析［J］.机械传动，2012，36（6）：71-73.

［6］ 廖汉元，孔建益.机械原理［M］.北京：机械工业出版社，2007：

179-187.