大温升速率加热器的全补偿复合控制
李万国 付永领 祁晓野
(北京航空航天大学 机械工程及自动化学院,北京100191)
对于某些材料的热学性能及热强度实验,需要对其表面同时进行大温升速率加热和施加机械压力载荷,由于机械加载装置覆盖了加热表面,采用辐射加热器加热比较困难,为此开发了接触式电加热器,其中的一项重要内容便是解决大温升速率的温度控制问题.
目前,采用辐射加热方式的电阻炉得到了广泛应用,其温控技术已相当成熟.常规的工业用途的电阻炉一般不要求大的温升速率,经典的PID控制方法就能获得满意的效果.温控精度要求高的场合,可以针对具体情况,在PID基础上进行改进,如李金堂等应用修改后的PID方法有效抑制了温度曲线拐点处的超调[1];为了抑制加热系统的大迟滞、非线性和时变特性对温控精度的影响,现代智能控制方法的应用越来越普遍,也收到了不错的效果,其中以模糊控制和神经网络控制最为常见,而控制器的具体结构又各不相同[2-3].关于高性能的辐射式加热器及温控技术,吴大方课题组开发了高超声速飞行器气动热环境模拟实验技术,其自行研制的石英灯辐射加热器达到了很高的指标,应用了模糊控制及神经网络控制方法的温控系统获得了很高的温度曲线跟踪精度[4].
在经典控制理论中,顺馈补偿方法属于开环控制方式,适用于可以预知性能的控制对象,跟踪性能好,稳定性强,配合反馈控制以补偿各种不可测或不可预知的干扰,可以获得更高的控制精度.这种方法在温控方面应用较少,而在机电系统控制方面应用很多,收到了不错的效果[5-8].
大温升速率接触式电加热技术是一种新的尝试,本文分析了加热器在大温升速率工况下数学模型的特殊性,指出其适于实现近似全补偿顺馈-反馈复合控制,继而对这种控制方法进行了大温升速率加热工况下的研究和实验.
1 加热器及其数学模型
1.1 加热器结构
为某绝热材料的性能实验专门开发了接触式加热器,其结构如图1所示.

图1 加热器结构
要求对材料表面进行加热,实现大温升速率斜坡升温-水平保温的温度曲线.
1.2 大温升速率下加热器的数学模型
对于一般的加热器,精确的数学模型往往为高阶系统,不过从实用意义上讲,可以建立如下的简化数学模型[9]:

式中,Ph为输入加热器的加热功率,W;Pd为流出发热体-被加热体系统的散热功率,W;Cs为大温升速率下加热器的等效热容量,J,其影响因素主要包括发热体、试件和中间传热介质的热容量;Tt为试件的被控温度,℃;vt为试件的被控温升速率,℃/s,vt=dTt/dt.
由式(1)可得,vt=(Ph-Pd)/Cs,可知只有当Ph≫Pd时,才可获得大的温升速率,而此时,可忽略散热功率,令Pd=0,代入式(1)得

由此可知,对于一般的加热器(炉),大温升速率下,试件被控温升速率与加热功率近似为静态的线性关系,二者之间几乎没有动态过程.
就本例而言,被控温度为试件加热面的表面温度Tt,也即是电热体的表面温度,电热体为热的良导体,且厚度很小,其表面温度与内部温度大致相同,因而电热体的温升速率也即是试件加热面的温升速率.对于这种特殊的工况,可视试件的吸热功率为系统等效散热功率,由于试件为绝热材料,本身热流很小,因而在大温升速率下,绝大部分加热功率用于加热电热体,等效热容量即为电热体的热容量Ch.
对于本例,令输入电热体的电功率即加热电源的输出功率为Pe,则Ph=Pe-Ped,式中Ped为非加热的电功率损耗,一般情况下会很小,则有Ph≈Pe,于是在大温升速率下有

同时考虑到系统延迟,在大温升速率下的数学模型可写为

式中,τ1为系统延迟时间,与加热电源、控温热电偶、试件和绝热层等部件的性能有关.一般而言,大功率的加热电源本身有一定的延迟时间,而热电偶的响应也存在一定的滞后.
对于纯电阻的电热体有
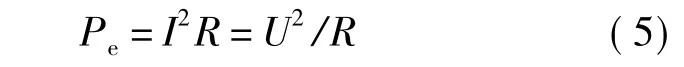
式中,I为加热电流有效值;U为加热电压有效值;R为电热体两电极间的电阻.根据式(3)可知,近似地有vt与I2和U2为线性关系.如果电源采用电流或电压控制方式,则电热体电阻随温度的变化会对系统的数学模型产生一定影响,为简便计,本文暂不考虑这一因素.
式(2)~式(4)为加热器在大温升速率工况下的数学模型,显示了加热器在该工况下的特殊性质,这个数学模型仅适用于大温升速率工况,如本例的斜坡升温段,而对于小温升速率、恒温控制不适用,如本例的保温段.保温段是恒温控制过程,属于常规工况,数学模型也很常规,此处不再分析.
2 控制策略
令大温升速率斜坡升温段为OA段,保温段为AB段,二者之间拐点处的过渡段为A段.就控制目标而言,OA段为恒温升速率,AB段为恒温.这两个阶段系统工作特性差别很大,因而可分别制定各自的控制律.为了保证没有过大的超调,同时避免过渡过程时间过长,A段也采取单独的控制律,因而总体上,系统可以采用三段控制律.系统动态框图如图2所示.

图2 控制系统结构示意图
图2中,s环节为微分环节,用于从给定的斜坡温度曲线计算给定的温升速率vtr,也可以根据加热要求直接给定vtr.
在OA段,只要能保证恒温升速率,就能够实现温度跟踪.而温升速率近似与输入电功率成线性关系,没有动态过程,因而采用基于给定值的顺馈控制器,很容易实现全补偿.根据式(3)和式(5)可以确定顺馈控制器的控制律,其结构如图3所示.
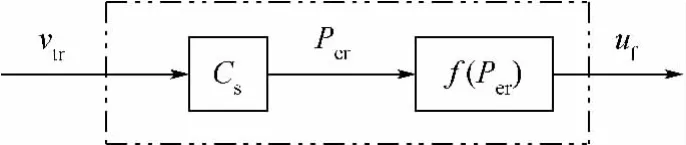
图3 顺馈控制器的结构
这里的顺馈控制器整体是一个静态环节.根据式(2)和式(3)可计算所需的加热功率Per,有时,控制器的输出不是加热功率信号,而是电流或者电压信号,因而需要用函数f(Per)来进行代数运算,计算出所需要的加热电流或电压作为顺馈控制器的输出量uf,由前面的分析可知,f(Per)未必是线性函数,本例中为二次函数.电热体热容量Ch可根据电热体材料的相关数据来计算,也可以和f(Per)一起通过实验数据来确定.事实上,由于前面推导数学模型时,忽略了散热功率、非加热功率损耗以及系统参数的时变因素,比如电热体电阻随温度的变化等,所以数学模型存在着一定的误差,如果能通过实验来测定,精度会更高些.
顺馈控制,属于开环控制方式,对于数学模型的误差、系统参数的变化以及不可测和不可预知的外干扰等因素带来的误差没有矫正能力,而且加热电源也存在一定的动态过程,因而这里的全补偿也只能是近似的,所以还需要配合温度闭环反馈控制以提高控制精度,图2中以PID-OA来实现.这里将这种近似全补偿顺馈-反馈复合控制方法简称为全补偿复合控制,而OA段的顺馈控制器和反馈控制器PID-OA的组合体便称为全补偿复合控制器.
事实上,由于所需的控制输出绝大部分由顺馈控制器提供,所以从总体上看,PID-OA的输出量应该很小,即:uf≫ub,从这个角度看,OA段的控制更接近于开环控制.
恒温的AB段很常规,可采用普通的PID控制器,如图2所示的PID-AB,即能获得满意的控制效果.拐点处的A段也可以采用PID控制,如图2中所示PID-A.控制过程中,需要根据一定的规则切换三段控制律,如图2中所示决策器,限于篇幅,此处不详细介绍.
在这个系统中,全补偿复合控制体现在OA段的恒温升速率的温度跟踪控制,其他阶段则采用了常规PID控制方法.如果将OA段的顺馈控制器除去,适当调整反馈控制器PID-OA,其他部分不变或稍作变动,则总体控制策略就成为了常规的PID控制方法.
上述两种方法都将进行实验.
3 实验结果
3.1 温升速率与输入电流(功率)的关系
为实现大温升速率控制,首先需要确定温升速率与输入功率或电流的关系,这里采用实验方法获取.实验设备采用单相交流可控硅电源,为电流控制方式,不同输入电流下的温升曲线如图4所示,可见恒定输入电流下(此时输入功率也基本恒定),温升曲线近似为直线,说明确定的加热功率对应着确定的温升速率.

图4 不同输入电流下的温升曲线
图4中9%~100%为输入电流相对值,此处以实验过程中最大温升速率所对应的输入电流为100%.
从图4可以得到不同输入电流和功率下的温升速率数值,以描点法获得温升速率相对输入电流和输入功率的曲线,分别如图5和图6所示.可见,温升速率与输入电流的关系近似为二次曲线,其二次拟合曲线与实验数据基本重合;而温升速率与输入功率的关系近似为直线,线性拟合曲线与实验数据也大致相符.由图6的线性拟合曲线,可以确定式(2)~式(4)中的参数Cs或Ch,从而使OA段的数学模型得以确定.

图5 温升速率-输入电流曲线

图6 温升速率-输入功率曲线
根据图5的逆曲线,可以确定顺馈控制器的控制律,它体现了控制器输出给电源的顺馈电流给定信号与输入的温升速率给定值的静态关系.
该实验验证了相关数学模型的正确性并为确定顺馈控制器的参数提供了依据.
3.2 温控实验
先后对常规PID控制方法和全补偿复合控制方法进行了实验.
按要求,温控曲线的AB段保温温度为800℃,OA段要求从初始温度上升到800℃的时间为24 s,温升速率约为31.5℃/s.首先进行了常规PID控制方法实验,经多次调整后的温控曲线如图7所示.继而调试了全补偿复合控制器,并进行了温控实验,结果一并显示在图7中,以进行比较.全补偿复合控制器的调试,关键在于顺馈控制器的参数,可以根据图5的拟合曲线求出OA段对应的顺馈电流相对值为82.3%,适当调整PID-OA,其他控制参数保持与常规PID方法相同.

图7 温控实验曲线
从图7可以看出,在保温段AB段,两种方法的效果相近,而在OA段,则有着明显的差异,A段响应受OA段结果影响很大,不好比较.全补偿复合控制方法对温升曲线的跟踪效果明显优于常规PID方法.二者在起始阶段都存在一个近似于死区特性的滞后效应,全补偿复合控制方法的滞后比常规PID方法小很多,相对而言,它能够很快追踪到并以较高精度跟随给定温升曲线,常规PID方法在大半时间内则产生了较大的跟踪误差.
二者在斜坡OA段的性能及其差异可以通过图8所示的实验过程中记录下来的电源输入输出曲线来解释.
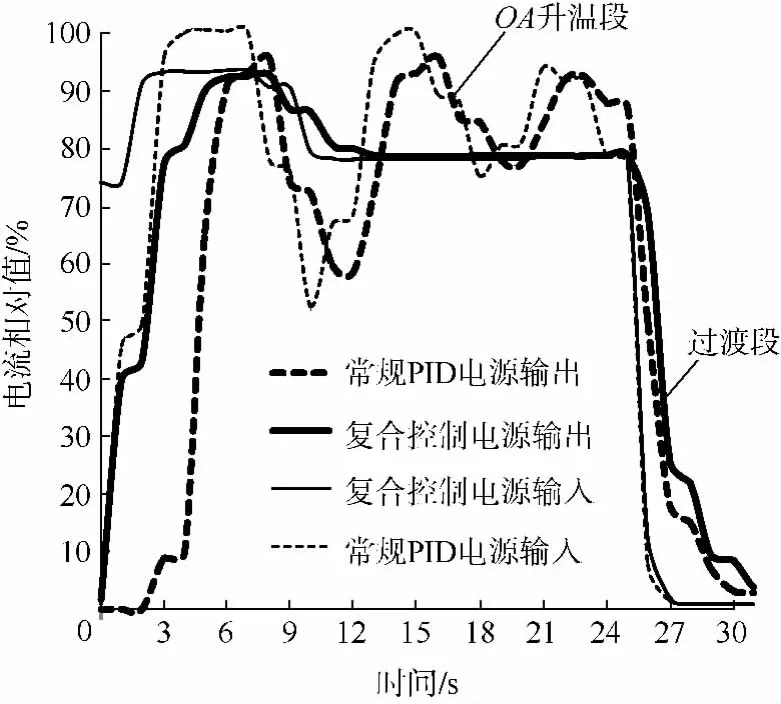
图8 实验过程中加热电源的输入输出曲线
采用常规PID方法,电源死区为2 s,而对于全补偿复合控制方法,电源没有表现出明显的死区特性.事实上,常规的加热器电源,为了防止电流和电压冲击,避免变流器元件损坏,往往在控制电路中采取了类似于电容充电特性的延时措施,本电源即是如此.如果输入信号过小,延时会很长,类似于死区,如果输入信号足够大,则输出上升较快,没有明显的死区特性.常规PID控制器给出的控制输出是从0递增而上的,在过程起始点处数值很小,因而死区较大,而全补偿复合控制器由于顺馈作用,在过程起始点直接给出了很大的控制信号,使得电源的输出滞后相对小了很多.从图8可以看出,在OA斜坡段起始部分,全补偿复合控制方法的加热电流迅速提升,明显超前于常规PID方法,而在OA斜坡的中后段,全补偿复合控制方法的加热电流基本恒定,但常规PID方法产生了很大的电流波动.由此也可以看出全补偿复合控制方法的跟踪性能更为平稳.温度上升到达拐点后,加热电流迅速下降,而在电流下降过程中,电源仍有滞后效应.
由图8还可以看出,全补偿复合控制下,升温段的后半段加热电流很稳定,其值约为79%,略小于拟合曲线的计算值82.3%,这一方面归因于拟合曲线不可避免的误差,另一方面也是因为在不同的工况下,系统参数也会有微小的差别.而附加的闭环控制器PID-OA也是完全必要的,它补偿了顺馈控制器的控制误差.不难判断,在斜坡升温段,控制器输出量的绝大部分来自于顺馈控制器,其实际调节过程接近于开环控制.
4 结论
通过对加热器在大温升速率下数学模型的特殊性分析以及相应的加热实验,可知在大温升速率加热过程中,温升速率与加热功率近似为静态的线性关系,基于顺馈-反馈复合控制结构,开发了全补偿复合控制方法,与常规PID控制方法对比进行了31.5℃/s的温升速率加热实验.结果表明,全补偿复合控制方法比常规PID方法具有更好的跟踪性能,加热过程更平稳,并且能够有效地抑制加热电源死区的影响.需要说明的是,由于前面所推导的数学模型适用于一般加热器,所以全补偿复合控制方法对一般加热器的大温升速率加热工况也是适用的.
References)
[1]李金堂,樊润洁.一种无超调钝角拐点的PID温控设计[J].电子设计工程,2010,18(8):82-85 Li Jintang,Fan Runjie.A design of PID temperature control without superscale obtuse angle and inflexion[J].Electronic Design Engineering,2010,18(8):82-85(in Chinese)
[2]Shi D Q,Gao G L,Gao Z W,et al.Application of expert fuzzy PID method for temperature control of heating furnace[J].Procedia Engineering,2012,29:257-261
[3]Hu L,Long W,Nie Z K.Development of PID neural network control system for temperature of resistance furnace[C]//2009 International Forum on Information Technology and Applications.Piscataway,NJ:IEEE Computer Society,2009,3:205-208
[4]吴大方,潘兵,高镇同,等.超高温、大热流、非线性气动热环境试验模拟及测试技术研究[J].实验力学,2012,27(3):255-271
Wu Dafang,Pan Bing,Gao Zhentong,et al.On the experimental simulation of ultra-high temperature,high heat flux,and nonlinear aerodynamic heating environment and thermal-mechanical testing technique[J].Journal of Experimental Mechanics,2012,27(3):255-271(in Chinese)
[5]Grzesiak L M,Tarczewski T.PMSM servo-drive control system with a state feedback and a load torque feedforward compensation[J].COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2013,32(1):364-382
[6]Seokmin H,Yonghwan O,Doik K,et al.Real-time walking pattern generation method for humanoid robots by combining feedback and feedforward controller[J].IEEE Transactions on Industrial Electronics,2014,61(1):355-364
[7]袁赣南,谭佳琳,周颋.顺馈-反馈技术在船舶姿态控制中的应用[J].系统仿真学报,2009,21(17):5524-5527
Yuan Gannan,Tan Jialin,Zhou Ting.Application of feedforwardfeedback control in control model of ship motion[J].Journal of System Simulation,2009,21(17):5524-5527(in Chinese)
[8]牛国臣,王巍,魏志强,等.基于力矩前馈和舵机角度补偿的力矩控制[J].北京航空航天大学学报,2013,39(3):300-304
Niu Guochen,Wang Wei,Wei Zhiqiang,et al.Torque control based on torque feedforward and rudder angle compensation[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(3):300-304(in Chinese)
[9]敖雯青,王寿增,张晋.电阻式加热炉温度控制数理模型研究[J].工业炉,2012,34(1):36-39 Ao Wenqing,Wang Shouzeng,Zhang Jin.Study on mathematical model of temperature control of resistance furnace[J].Industrial Furnace,2012,34(1):36-39(in Chinese)

